Содержание
- 2. Wprowadzenie do projektowania algorytmów Alagić S., Arbib M.A. - WNT 1982 „Projektowanie programów poprawnych i dobrze
- 3. Podstawowa wiedza o budowie algorytmów . Algorytmy mają budowę modularną. Moduł (algorytm dla jednego podzadania): jest
- 4. Każdy dowolnie złożony algorytm można zbudować z trzech tylko konstrukcji podstawowych, nazywanych strukturami, są to :
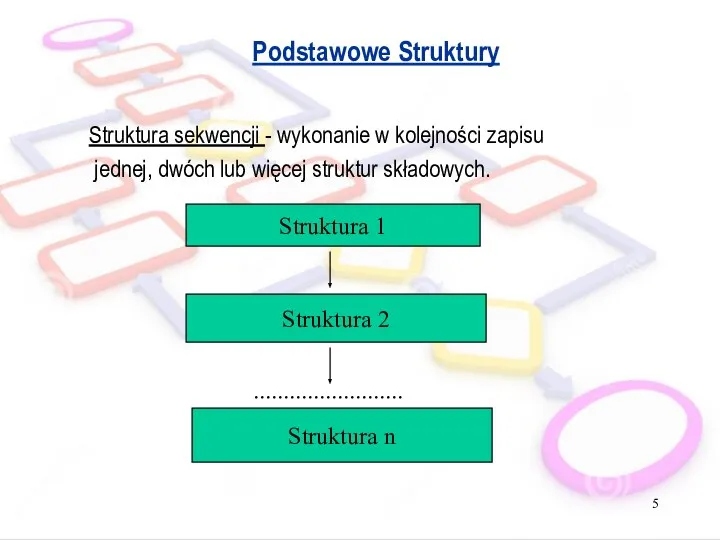
- 5. Podstawowe Struktury Struktura sekwencji - wykonanie w kolejności zapisu jednej, dwóch lub więcej struktur składowych. Struktura
- 6. Algorytmy szeregowe Algorytm nazywamy szeregowym, jeśli spełniona jest zależność gdzie n+1 ilość operacji w algorytmie oi
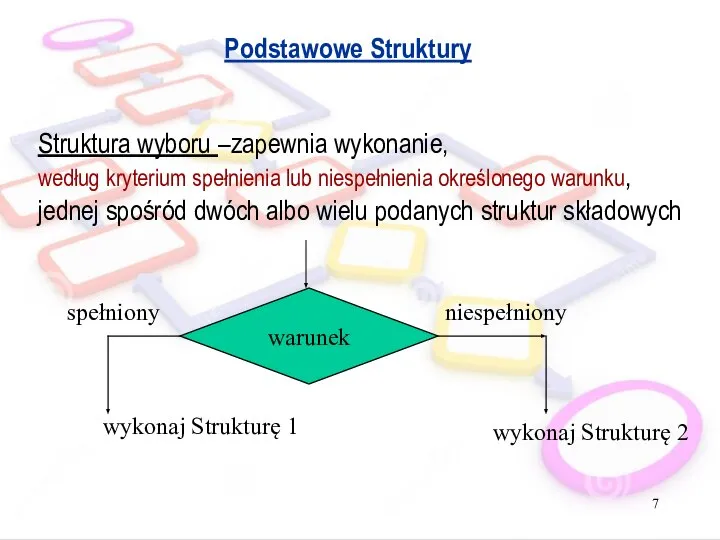
- 7. Podstawowe Struktury warunek Struktura wyboru –zapewnia wykonanie, według kryterium spełnienia lub niespełnienia określonego warunku, jednej spośród
- 8. Przykład poszukiwania rozwiązań problemu Wyznaczanie NWD Szukany jest NWD (m,n) - największy wspólny podzielnik liczb naturalnych
- 9. Wyznaczania wspólnego podzielnika dwóch liczb naturalnych – algorytm Euklidesa Metoda 2 Przyjmijmy, że n>m, wtedy n=q*m+r
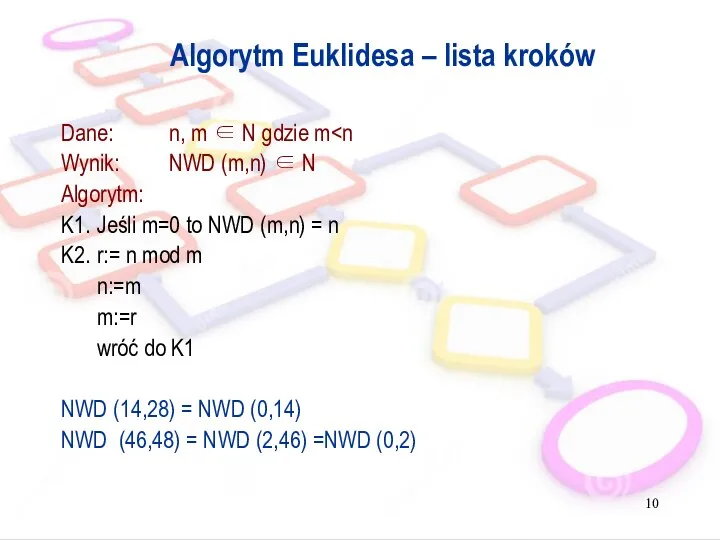
- 10. Algorytm Euklidesa – lista kroków Dane: n, m ∈ N gdzie m Wynik: NWD (m,n) ∈
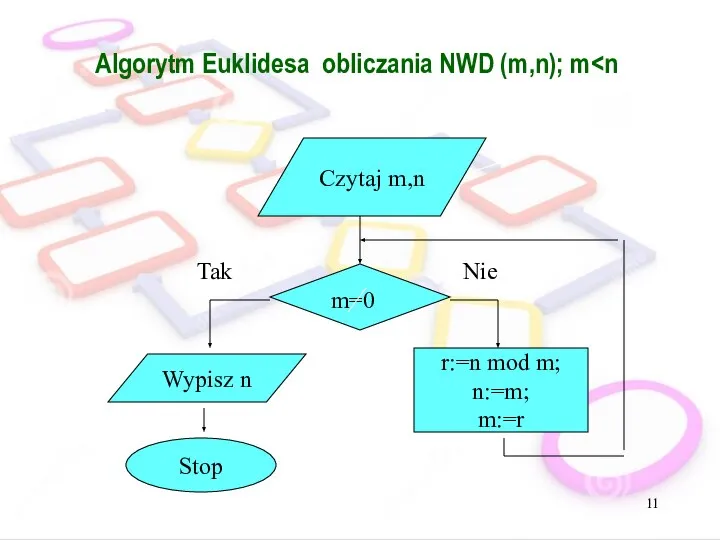
- 11. Algorytm Euklidesa obliczania NWD (m,n); m m=0 Stop Tak r:=n mod m; n:=m; m:=r Nie Czytaj
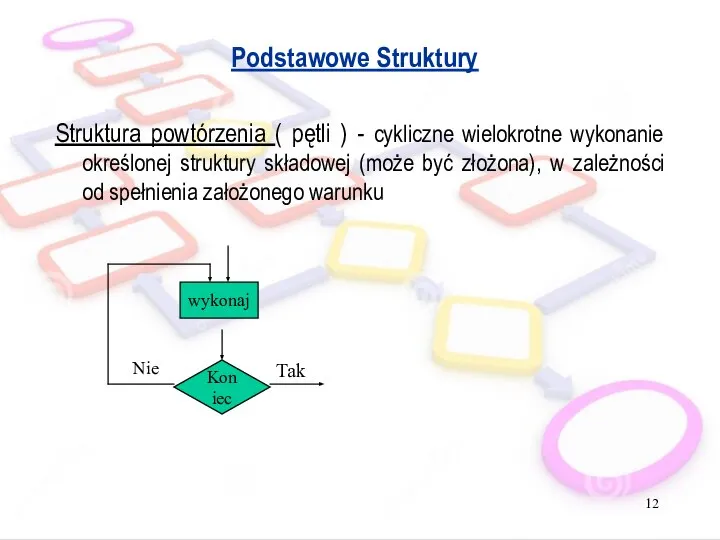
- 12. Podstawowe Struktury Struktura powtórzenia ( pętli ) - cykliczne wielokrotne wykonanie określonej struktury składowej (może być
- 13. Iteracja Iteracja – powtarzanie określonego ciągu operacji na pewnych elementach zbioru danych; Rodzaje iteracji ( pętli)
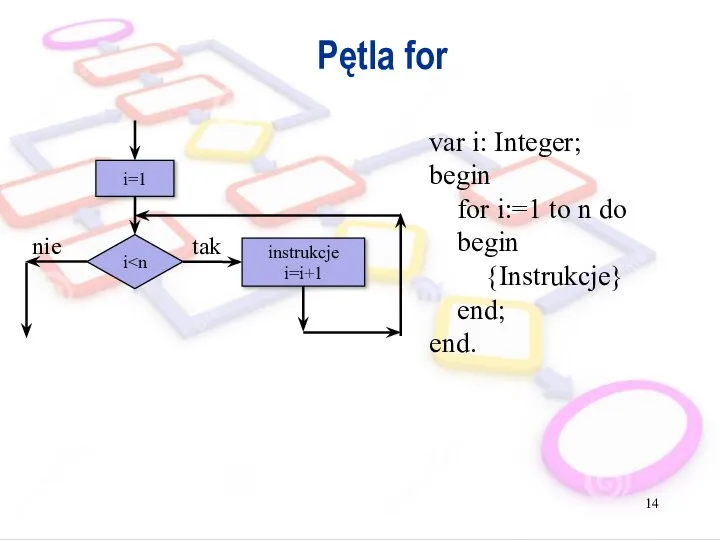
- 14. Pętla for i i=1 tak instrukcje i=i+1 nie var i: Integer; begin for i:=1 to n
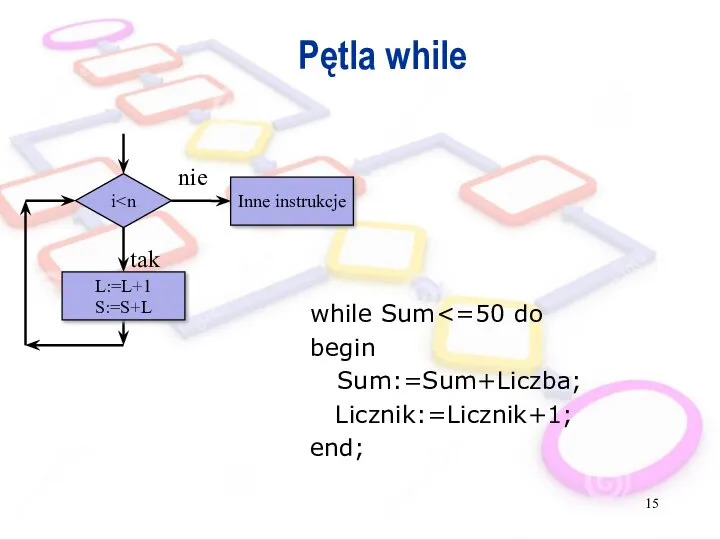
- 15. Pętla while while Sum begin Sum:=Sum+Liczba; Licznik:=Licznik+1; end; i tak Inne instrukcje nie L:=L+1 S:=S+L
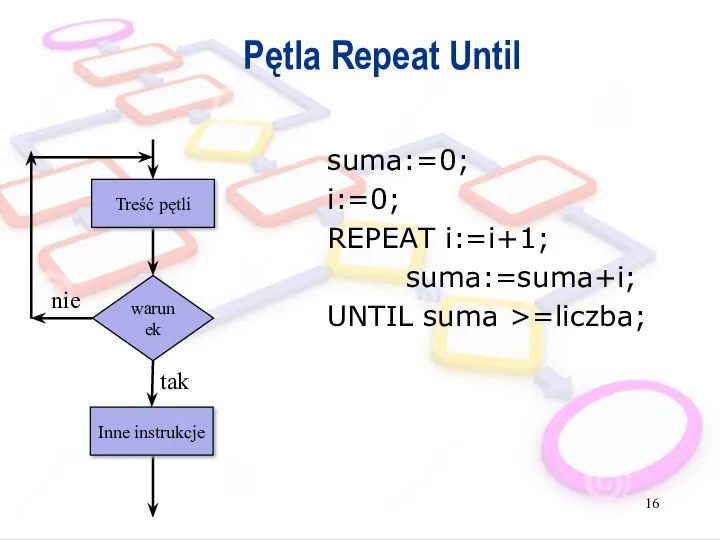
- 16. Pętla Repeat Until suma:=0; i:=0; REPEAT i:=i+1; suma:=suma+i; UNTIL suma >=liczba; warunek tak Inne instrukcje nie
- 17. Przykłady problemów Przeszukiwanie, filtrowanie, sortowanie zbiorów danych; Statystyczna analiza danych; obliczanie parametrów statystycznych : średnich (arytmetycznej,
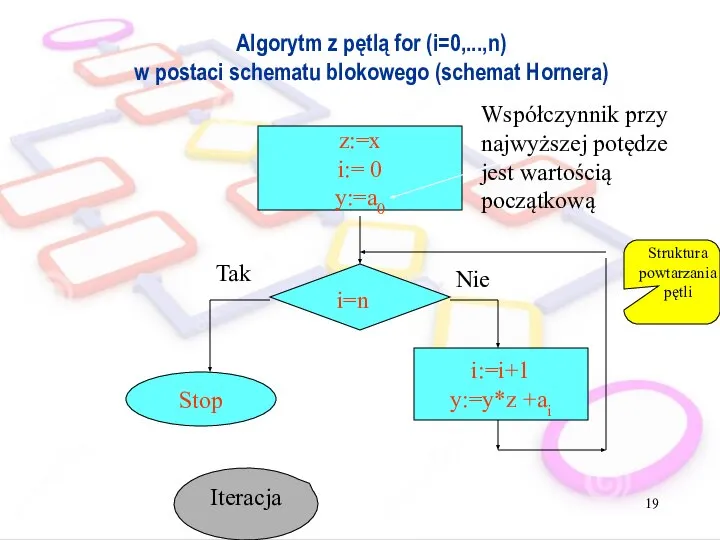
- 18. Obliczanie wartości wielomianu Wn (x) dla określonej wartości wg schematu Hornera Tradycyjny zapis wielomianu Wn(x) =
- 19. Algorytm z pętlą for (i=0,...,n) w postaci schematu blokowego (schemat Hornera) i=n z:=x i:= 0 y:=a0
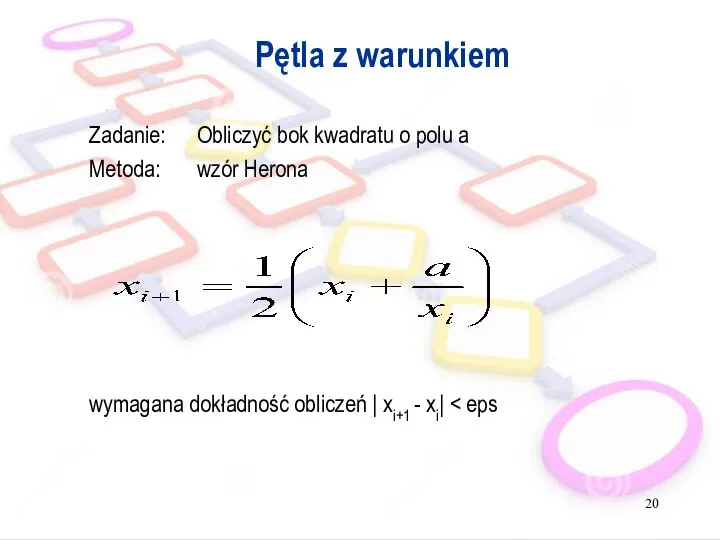
- 20. Pętla z warunkiem Zadanie: Obliczyć bok kwadratu o polu a Metoda: wzór Herona wymagana dokładność obliczeń
- 21. Algorytm obliczania pierwiastka kwadratowego z danej liczby wg wzoru Herona Dane: Liczba pierwiastkowana: a Pierwsze przybliżenie
- 22. Algorytm Newtona Raphsona Dane: Liczba pierwiastkowana: a Pierwsze przybliżenie pierwiastka kwadratowego z danej liczby: p dokładność
- 23. Iteracja kończąca się i iteracja nieskończona Kryteria zakończenia obliczeń (działań) w algorytmie iteracyjnym: wykonanie podanej liczby
- 24. Zadania Opracować algorytmy na : obliczanie sumy i wartości średniej n danych liczb obliczanie iloczynu n
- 25. Rekurencja Przykłady definicji rekurencyjnych w matematyce Rekurencja jest szczególnie silnym narzędziem w matematyce, przykłady: Liczby naturalne:
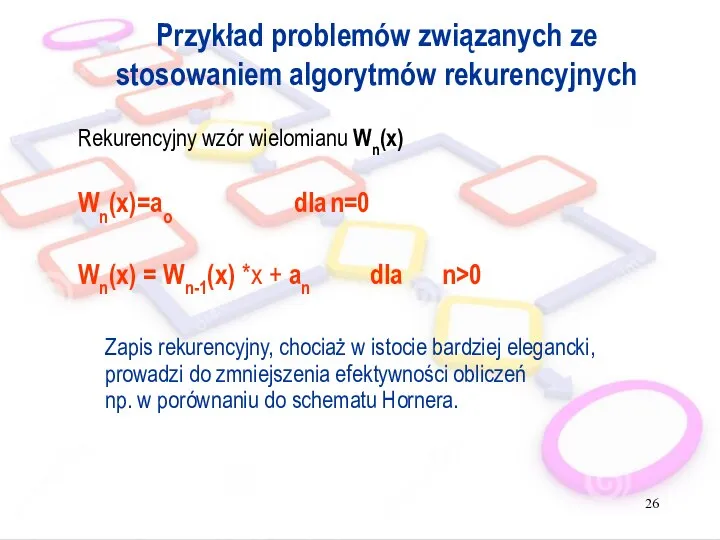
- 26. Przykład problemów związanych ze stosowaniem algorytmów rekurencyjnych Rekurencyjny wzór wielomianu Wn(x) Wn(x)=ao dla n=0 Wn(x) =
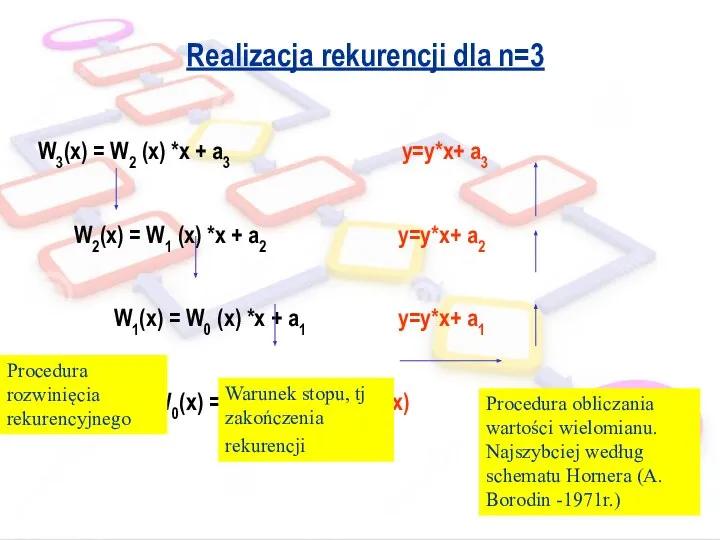
- 27. Realizacja rekurencji dla n=3 W3(x) = W2 (x) *x + a3 y=y*x+ a3 W2(x) = W1
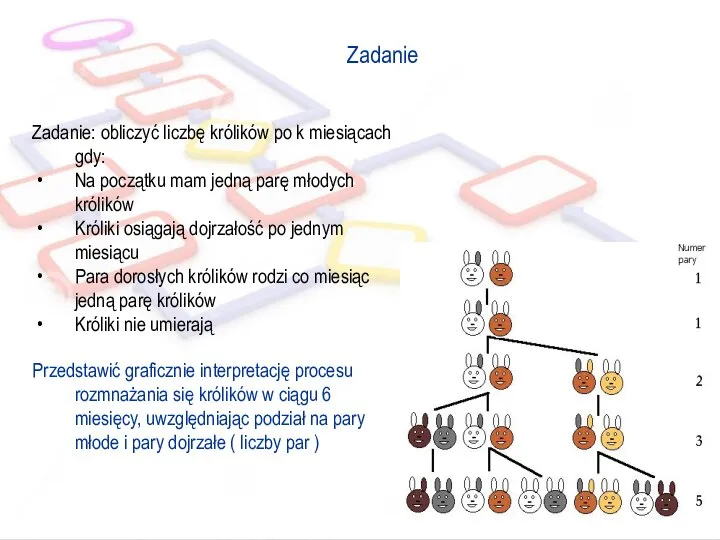
- 28. Zadanie Zadanie: obliczyć liczbę królików po k miesiącach gdy: Na początku mam jedną parę młodych królików
- 29. Ciąg Fibonacciego W 1202 roku Leonard z Pizy zwany Fibonaccim (synem Bonacciego) w dziele Liber abaci
- 30. Problemy z rekurencją: występowanie dublujących się obliczeń Obliczanie parametrów ciągu rekurencyjnego wykonane bezpośrednio na podstawie wzoru
- 31. Jawna postać liczb Fibonacciego Jawny wzór na n - ty wyraz ciągu Fibonacciego, zwany wzorem Bineta,
- 32. Ciekawostki zamiast podsumowania Zastosowania liczb Fibonacciego – złota liczba Złota liczba granica ciągu F(n+1)/F(n) czyli ilorazów
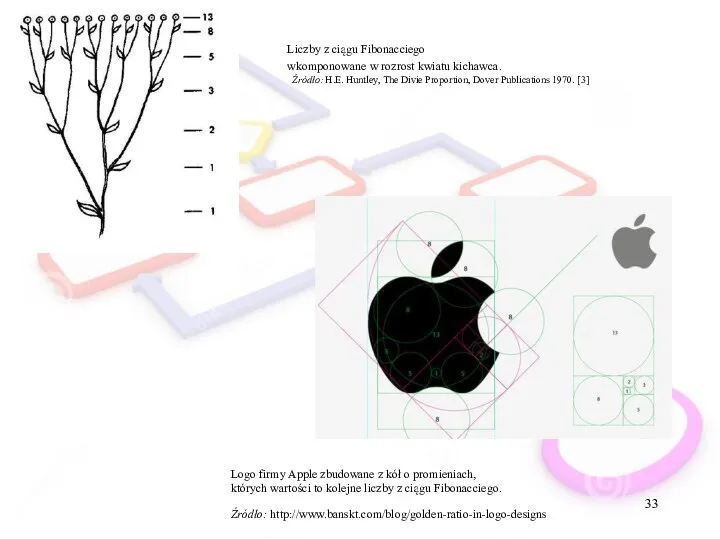
- 33. Liczby z ciągu Fibonacciego wkomponowane w rozrost kwiatu kichawca. Źródło: H.E. Huntley, The Divie Proportion, Dover
- 34. Złoty podział i liczby Fibonacciego Złoty podział - podział harmoniczny, dla liczby a, jest to przedstawienie
- 35. Schemat złotego podziału prostokąta Złota spirala Zdjęcie rentgenowskie muszli łodzika. Źródło: H.E. Huntley, The Divine Proportion,
- 37. Скачать презентацию




















 ПономаренкоГалль4.06
ПономаренкоГалль4.06 Технология машиностроения
Технология машиностроения Презентація
Презентація 20151216_urok_no15_formirovanie_srednevekovyh_gorodov
20151216_urok_no15_formirovanie_srednevekovyh_gorodov Газета №6. I love english
Газета №6. I love english диагностика 4-5 лет
диагностика 4-5 лет Машинные швы
Машинные швы Инструкция по диагностике проблем мотора вентилятора отопителя
Инструкция по диагностике проблем мотора вентилятора отопителя Реализация приоритетного проекта Формирование комфортной городской среды на территории МО Уемское на 2018 год
Реализация приоритетного проекта Формирование комфортной городской среды на территории МО Уемское на 2018 год Доклад директора ГБУ Жилищник района Котловка
Доклад директора ГБУ Жилищник района Котловка Архитектура
Архитектура Работы нулевого цикла
Работы нулевого цикла Конструирование и моделирование швейных изделий (7 класс)
Конструирование и моделирование швейных изделий (7 класс) Управление денежными потоками организации
Управление денежными потоками организации BAE Systems, Inc. Sectors at a Glance
BAE Systems, Inc. Sectors at a Glance “Discovery Investigation Agency ”
“Discovery Investigation Agency ” Электрические приборы в доме
Электрические приборы в доме Проф. требования. Методы конструирования
Проф. требования. Методы конструирования Колаж книжкові виставки
Колаж книжкові виставки Первые работы Фобс
Первые работы Фобс 20180109_orlovskaya_oblast-80_let
20180109_orlovskaya_oblast-80_let 220722 Маркетинг ивент_фотозона
220722 Маркетинг ивент_фотозона Стали и серые чугуны
Стали и серые чугуны Понятие о резьбе
Понятие о резьбе Знакообразование
Знакообразование Светлая память всем, кого с нами нет
Светлая память всем, кого с нами нет Вопросы для обсуждения комедии А.В.Сухово-Кобылина Свадьба Кречинского в постановке Театра им. Моссовета
Вопросы для обсуждения комедии А.В.Сухово-Кобылина Свадьба Кречинского в постановке Театра им. Моссовета Аналоговые перемножетели напряжений
Аналоговые перемножетели напряжений