Содержание
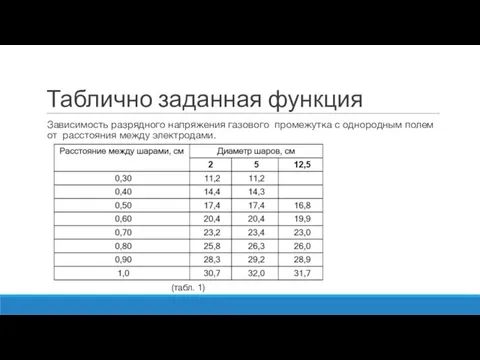
- 2. Таблично заданная функция Зависимость разрядного напряжения газового промежутка с однородным полем от расстояния между электродами. (табл.
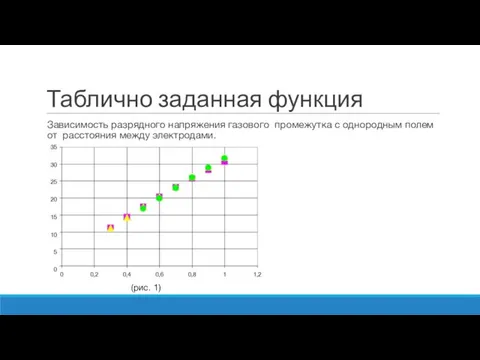
- 3. Таблично заданная функция Зависимость разрядного напряжения газового промежутка с однородным полем от расстояния между электродами. (рис.
- 4. Таблично заданная функция Зависимость разрядного напряжения газового промежутка с однородным полем от расстояния между электродами. (табл.
- 5. Аппроксимация таблично заданных функций (приближение функций, заданных таблично) Таблица - дискретное множество значений аргумента (xi) поставленое
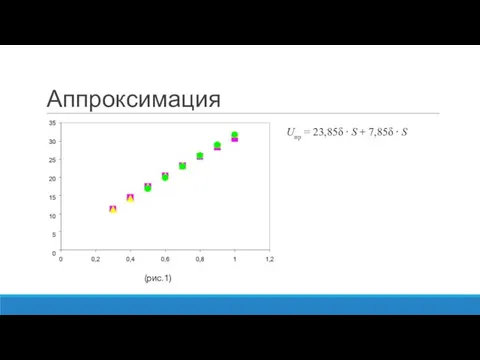
- 6. Аппроксимация Uпр = 23,85δ ⋅ S + 7,85δ ⋅ S (рис.1)
- 7. Критерии аппроксимации Метод наименьших квадратов. Мерой близости аппроксимирующей функции f(x) к табличной является величина:00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 Наилучшее приближение
- 8. Сглаживание функций - сглаживающий сплайн. Сглаживающий сплайн - это метод сглаживания аппроксимации кривой набора зашумлённых исходных
- 9. Примечания: параметр сглаживания, контролирующий соотношение между точностью воспроизведения данных и «неровностью» аппроксимирующей функции. Интеграл вычисляется по
- 10. Метод наименьших квадратов Это один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений,
- 11. Основной принцип метода наименьших квадратов При замене точного (неизвестного) параметра модели приблизительным значением необходимо минимизировать разницу
- 12. Приближение МНК Так же с помощью МНК из экспериментальных данных сделать приблизительный расчет (рисунок 2): (рис.
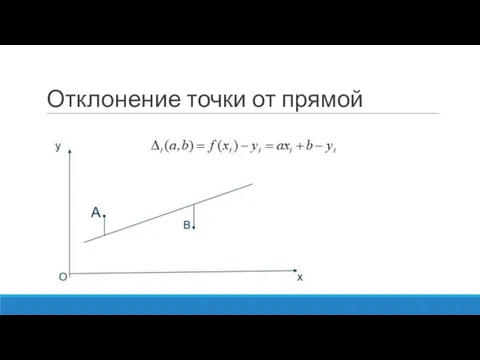
- 13. Отклонение точки от прямой
- 14. Как учесть отклонение всех точек? В рамках метода наименьших квадратов минимизируется величина: Суммарное отклонение всех точек
- 15. Метод наименьших квадратов Пусть нам известно оптимальное значение a. Тогда S зависит только от b. Для
- 16. Суть метода наименьших квадратов Рассмотрим применение МНК в случае применения линейного полинома: φ(х) = y =
- 17. Суть метода наименьших квадратов Из уравнения (1) следует, что (2) Чем меньше числа δi по абсолютной
- 18. Суть метода наименьших квадратов Условия минимума SS будут: (5) (6) Уравнения (6) и (7) можно записать
- 19. Пример Пример. В результате эксперимента получены значения x и y, сведенные в таблицу 2: Найти аппроксимирующую
- 21. Скачать презентацию














 клуб бардовской песни
клуб бардовской песни 20110527_Interaktivnyy_plakat_Sinkveyn
20110527_Interaktivnyy_plakat_Sinkveyn Гарнизонная церковь в честь Покрова Богородицы в г. Орле
Гарнизонная церковь в честь Покрова Богородицы в г. Орле Предприятие по добыче, обогащению и переработке руд Тырныаузского вольфрамо-молибденового месторождения. Гидрометаллургический
Предприятие по добыче, обогащению и переработке руд Тырныаузского вольфрамо-молибденового месторождения. Гидрометаллургический Бейджики 1-Б
Бейджики 1-Б Сервис буровых растворов
Сервис буровых растворов 2 Kap2
2 Kap2 outlook
outlook Проектирование изделий из тканей, содержащих искусственные волокна, из искусственных кож, замши, тканей с пленочным покрытием
Проектирование изделий из тканей, содержащих искусственные волокна, из искусственных кож, замши, тканей с пленочным покрытием Программируемые логические контроллеры
Программируемые логические контроллеры 20140123_agressiya_1_u_detey_kak_sledstvie_uvlecheniya_kompyuternymi_-_kopiya_0
20140123_agressiya_1_u_detey_kak_sledstvie_uvlecheniya_kompyuternymi_-_kopiya_0 БОШКА
БОШКА Работа с фрагментами в Paint
Работа с фрагментами в Paint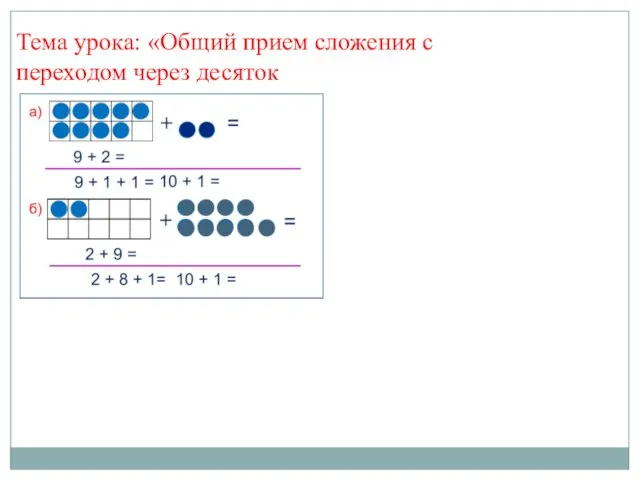 Общий прием сложения с переходом через десяток
Общий прием сложения с переходом через десяток kiber
kiber Портфолио Арсенұлы Әлнұр Арсен
Портфолио Арсенұлы Әлнұр Арсен Асинхронные машины. Конструкция и принцип действия
Асинхронные машины. Конструкция и принцип действия педсовет авг 20
педсовет авг 20 ФГОС ОО формирование компетенций ср-ми ДО
ФГОС ОО формирование компетенций ср-ми ДО Резюме2 (2)
Резюме2 (2) Угловые соединения
Угловые соединения Смена владельца сим-карты, МТС
Смена владельца сим-карты, МТС 28 листы рекомендаций
28 листы рекомендаций Ребенок с ограниченными возможностями здоровья в современном российском обществе
Ребенок с ограниченными возможностями здоровья в современном российском обществе Переробка та утилізація відходів нафтопереробної галузі
Переробка та утилізація відходів нафтопереробної галузі Очистные сооружения хозяйственно-бытовых стоков
Очистные сооружения хозяйственно-бытовых стоков Результаты работы с механизированным фондом скважин ЦДНГ №8 за 1 кв. 2015 г
Результаты работы с механизированным фондом скважин ЦДНГ №8 за 1 кв. 2015 г Мультимедийное оборудование в профессиональной деятельности
Мультимедийное оборудование в профессиональной деятельности