Содержание
- 3. Литература 1. Васильев А.Н. MATLAB. Самоучитель. Практический подход. – СПб.: Наука и техника, 2012. – 448
- 4. Цифровая и аналоговая обработка сигналов
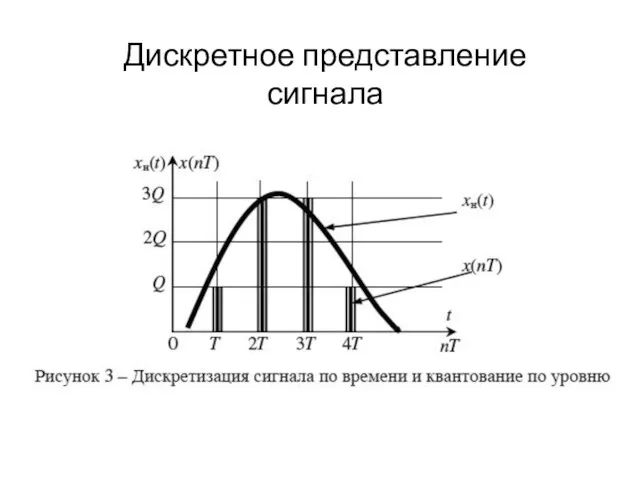
- 5. Дискретное представление сигнала
- 6. Достоинства дискретных систем 1. Возможность реализации сколь угодно сложных алгоритмов обработки сигналов. 2. Простота перестройки алгоритмов.
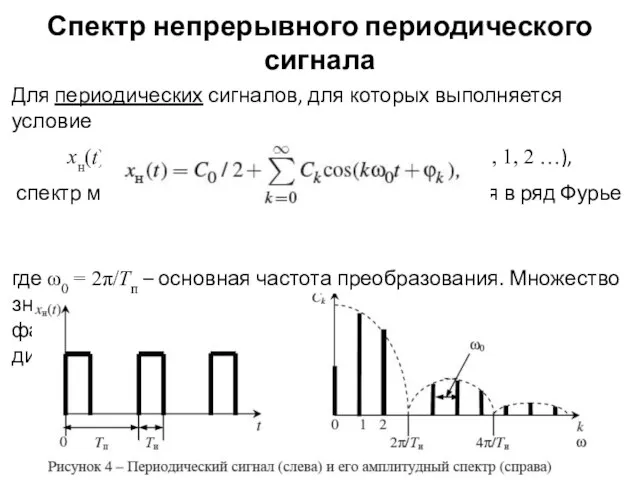
- 7. Спектр непрерывного периодического сигнала Для периодических сигналов, для которых выполняется условие xн(t) = xн(t + kТп)
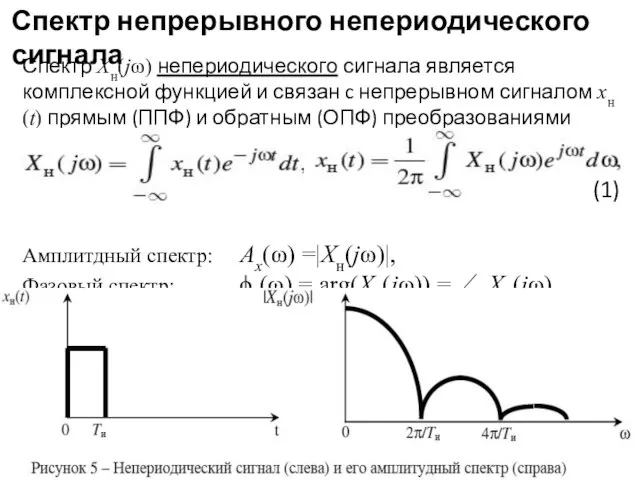
- 8. Спектр Xн(jω) непериодического сигнала является комплексной функцией и связан c непрерывном сигналом xн(t) прямым (ППФ) и
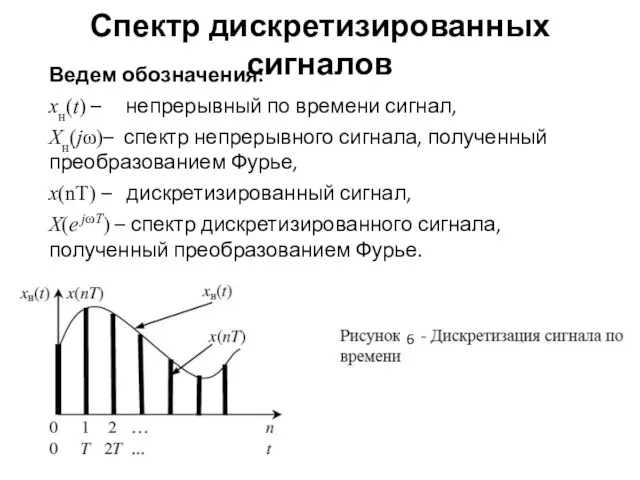
- 9. Спектр дискретизированных сигналов Ведем обозначения: xн(t) – непрерывный по времени сигнал, Xн(jω)– спектр непрерывного сигнала, полученный
- 10. Спектры дискретизированных и непрерывных сигналов, теорема отсчетов
- 11. Прямое и обратное преобразования Фурье для дискретизированного сигнала записываются в виде: (2) Преобразование Фурье дискретизированного сигнала
- 12. Из формул (1) и (3) следует: Разобьем ось частот ω на отрезки размером ωд: x(nT) =
- 13. Из сравнения (4) и (2) следует, что Спектр дискретизированного сигнала состоит с точностью до множителя 1/Т
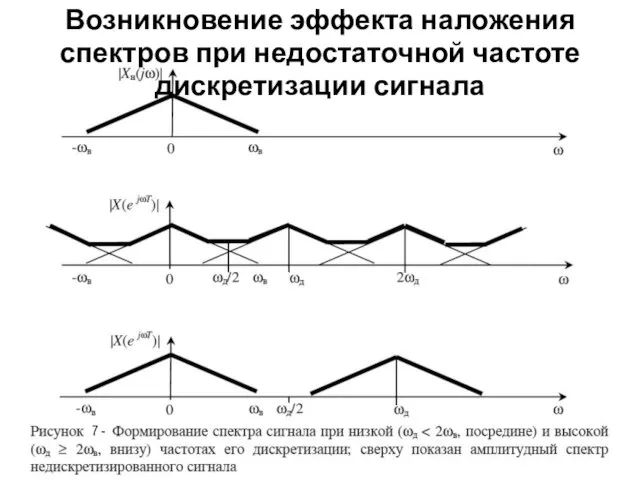
- 14. Возникновение эффекта наложения спектров при недостаточной частоте дискретизации сигнала 7 -
- 15. Восстановление непрерывного сигнала по его дискретным отсчетам
- 16. Если Xн(jω) = 0 при |ω| > ωв, и ωд ≥ 2ωв, эффект наложения спектров отсутствует,
- 17. Непрерывный сигнал xн(t) получается суммированием функций ϕn(t) с весами, определяемыми значениями отсчетов дискретного сигнала x(nT). Рассмотрим
- 18. Рассмотрим некоторые характерные точки функции ϕn(t). При n = 0 ϕ0(t) = 0 при ⇒ ϕ0(t)
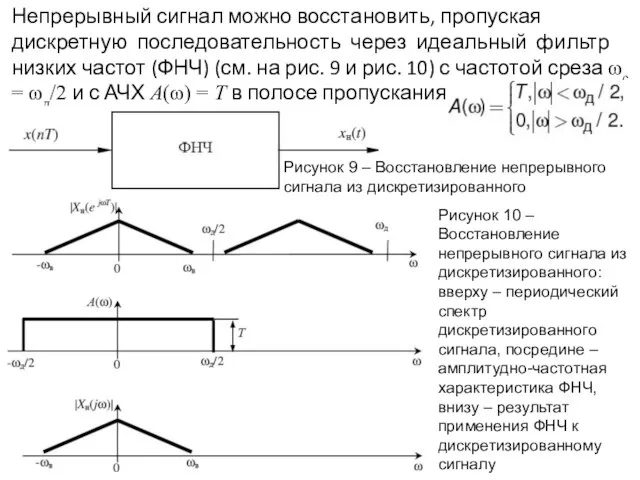
- 19. Непрерывный сигнал можно восстановить, пропуская дискретную последовательность через идеальный фильтр низких частот (ФНЧ) (см. на рис.
- 20. Линейные дискретные системы
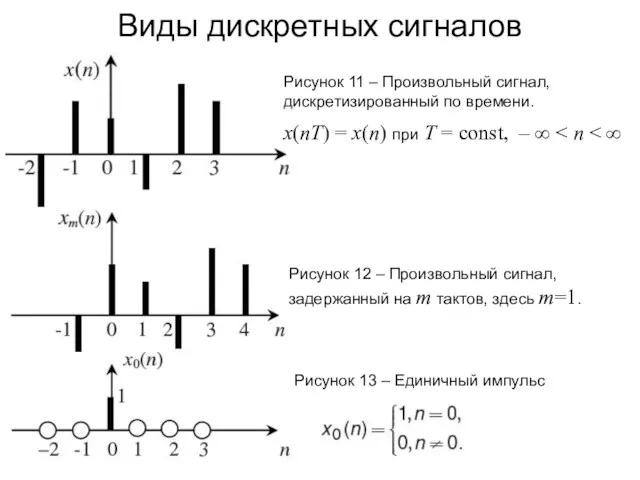
- 21. Рисунок 11 – Произвольный сигнал, дискретизированный по времени. x(nT) = x(n) при Т = const, –
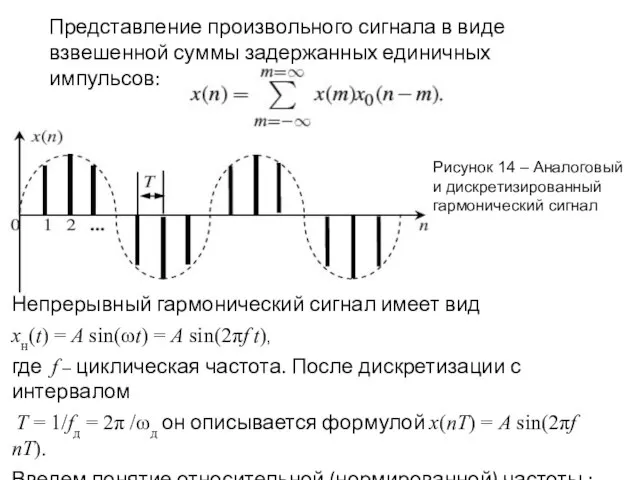
- 22. Представление произвольного сигнала в виде взвешенной суммы задержанных единичных импульсов: Рисунок 14 – Аналоговый и дискретизированный
- 23. Рисунок 15 – Графические обозначения операций над дискретными сигналами Операции над дискретными сигналами В комплексной форме
- 24. Свойства и параметры дискретных систем
- 25. Линейность Линейная сумма сигналов на входе системы вызывает на выходе сигнал в виде линейной суммы соответствующих
- 26. Описание работы системы с помощью формулы свертки Было показано, что любой сигнал можно представить в виде
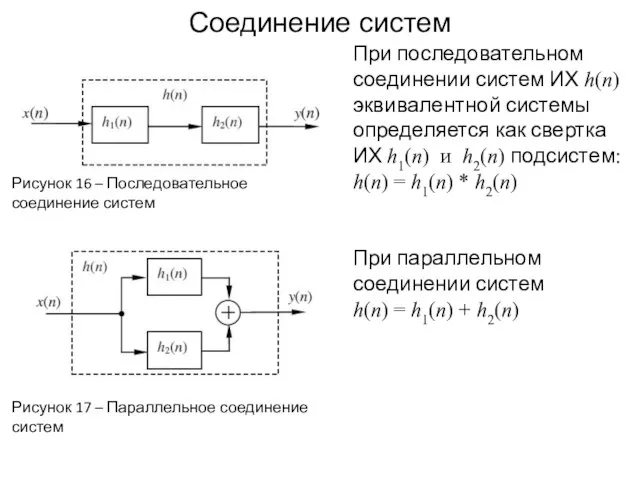
- 27. Соединение систем Рисунок 16 – Последовательное соединение систем Рисунок 17 – Параллельное соединение систем При последовательном
- 28. Устойчивость системы Система называется устойчивой, если ограниченный по величине сигнал на входе вызывает ограниченный по величине
- 29. Устойчивость системы Докажем достаточность выполнения условия Предположим, что это условие выполняется. Ограничим величину входного сигнала |x(n)|
- 30. Частотная характеристика системы Частотная характеристика (ЧХ) определяет реакцию системы на входной гармонический сигнал. Пусть на входе
- 31. Частотная характеристика системы Частотная характеристика H(e jωT) = yω(nT) / xω(nT) = [Ay(ω) / Ax(ω)] e
- 32. Методы вычисления частотной характеристики Сформируем на входе системы комплексную синусоиду следующего вида: x(nT) = e jωnT
- 33. Методы вычисления частотной характеристики Вычислим входной сигнал x(nT) и выходной сигнал y(nT) через их Фурье-спектры X(e
- 34. Свойства частотной характеристики ЧХ есть непрерывная функция частоты ω. ЧХ – периодическая функция с периодом, равным
- 35. Преобразование Лапласа Z-преобразование Прямое и обратное преобразования Лапласа соответственно описываются формулами где s – переменная Лапласа,
- 36. Свойства Z-преобразования 1. Свойство линейности Если Z[x1(n)] = X1(z) и Z[x2(n)] = X2(z), то Z[а1x1(n) +
- 37. Связь передаточной функции с частотной характеристикой ЧХ H(e jω) может быть получена из передаточной функции H(z)
- 38. Цифровые фильтры
- 39. Разностные уравнения Система фильтрации сигнала как и системы вообще могут быть описаны дифференциальными уравнениями связывающим входной
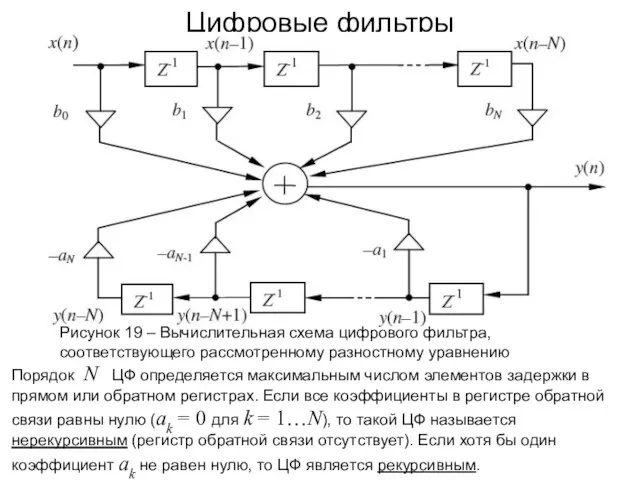
- 40. Цифровые фильтры Рисунок 19 – Вычислительная схема цифрового фильтра, соответствующего рассмотренному разностному уравнению Порядок N ЦФ
- 41. Пример цифрового фильтра Рассмотрим рекурсивный фильтр 1-го порядка (см. рис. 20), описываемый разностным уравнением y(n) =
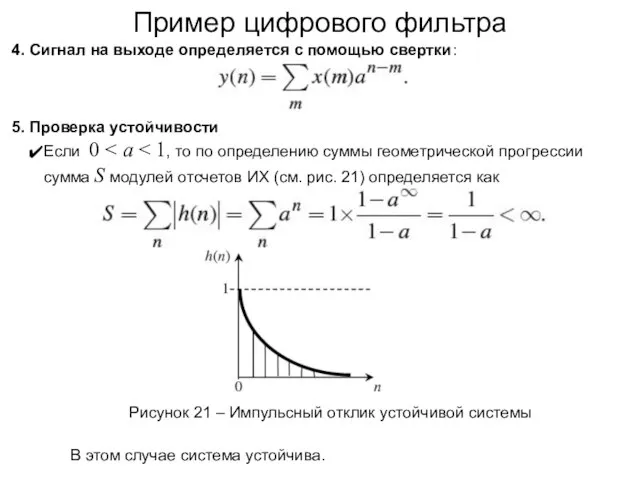
- 42. Пример цифрового фильтра 4. Сигнал на выходе определяется с помощью свертки: 5. Проверка устойчивости Если 0
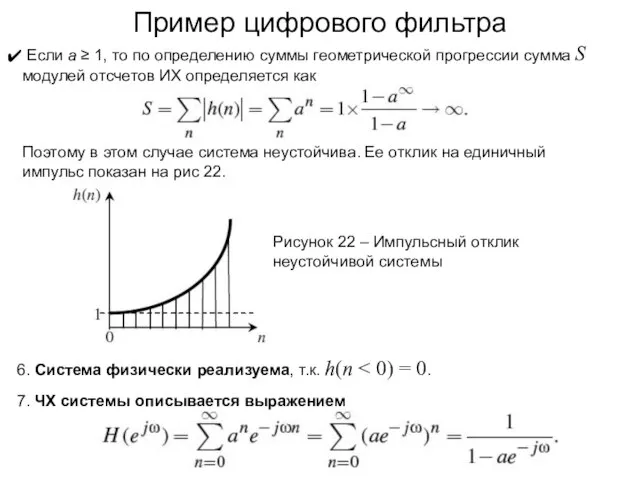
- 43. Пример цифрового фильтра Если a ≥ 1, то по определению суммы геометрической прогрессии сумма S модулей
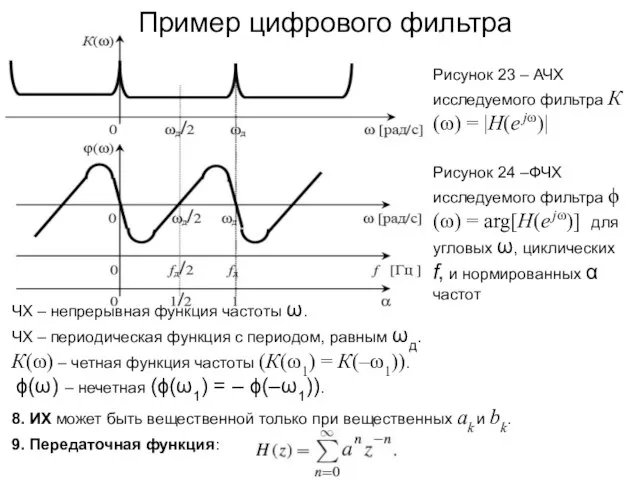
- 44. Рисунок 23 – АЧХ исследуемого фильтра К(ω) = |H(e jω)| Рисунок 24 –ФЧХ исследуемого фильтра ϕ(ω)
- 45. Передаточная функция может быть вычислена через коэффициенты разностного уравнения a0 = 1 ⇒ . Выполнив Z-преобразование
- 46. Полюса и нули передаточной функции Разложим числитель и знаменатель передаточной функции H(z) на множители: Передаточная функция
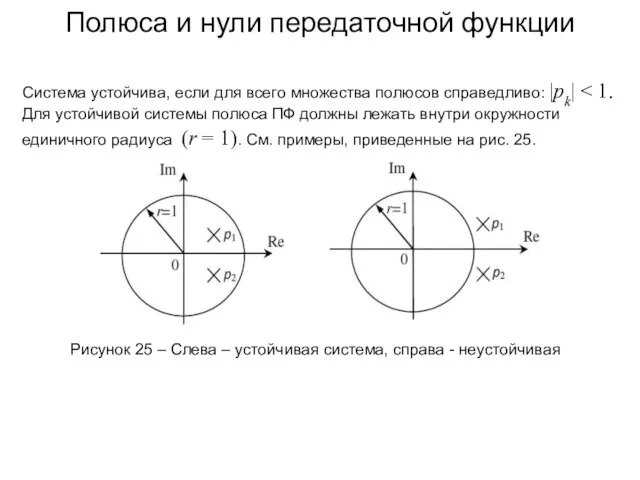
- 47. Полюса и нули передаточной функции Система устойчива, если для всего множества полюсов справедливо: |pk| Рисунок 25
- 48. Полюса и нули передаточной функции Проанализируем устойчивость системы, описанной разностным уравнением y(n) = x(n) + a
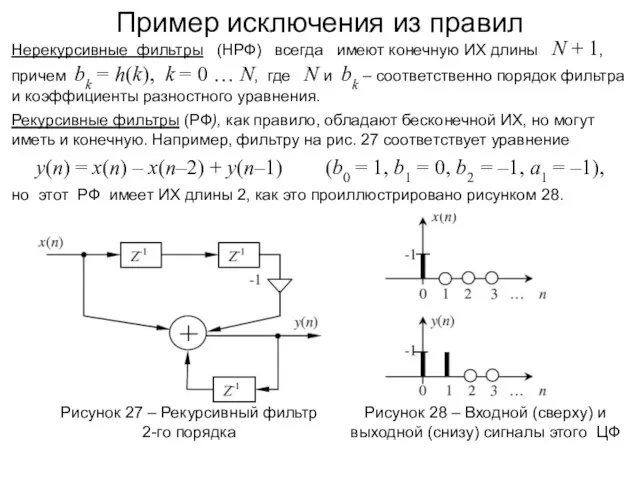
- 49. Пример исключения из правил Нерекурсивные фильтры (НРФ) всегда имеют конечную ИХ длины N + 1, причем
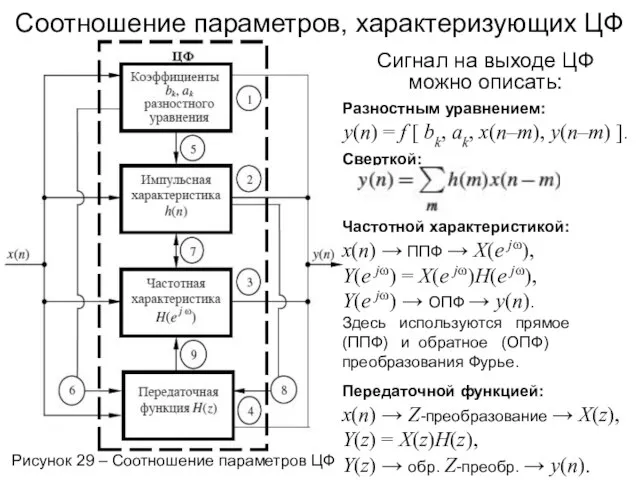
- 50. Соотношение параметров, характеризующих ЦФ Рисунок 29 – Соотношение параметров ЦФ Сигнал на выходе ЦФ можно описать:
- 51. Связь характеристик ЦФ: 5. Разностного уравнения и импульсной характеристики: подаем на вход единичный импульс: x(n) =
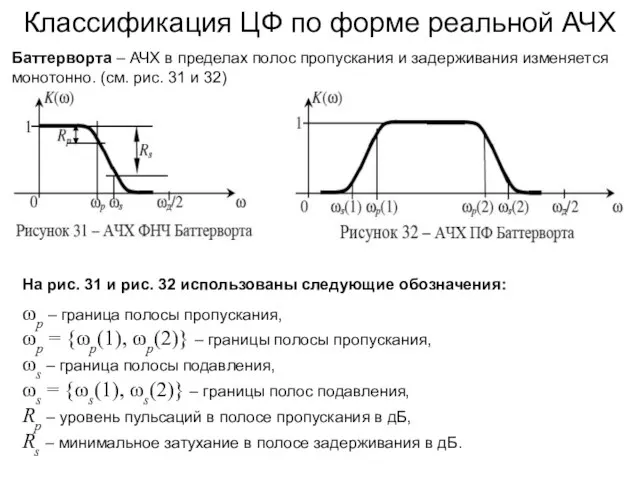
- 52. Классификация ЦФ по форме АЧХ Рисунок 30 – Классификация ЦФ по параметрам полосы пропускания: а –
- 53. Классификация ЦФ по форме реальной АЧХ Баттерворта – АЧХ в пределах полос пропускания и задерживания изменяется
- 54. Классификация ЦФ по форме АЧХ Чебышева 1 рода – имеются пульсации в полосе пропускания, крутизна АЧХ
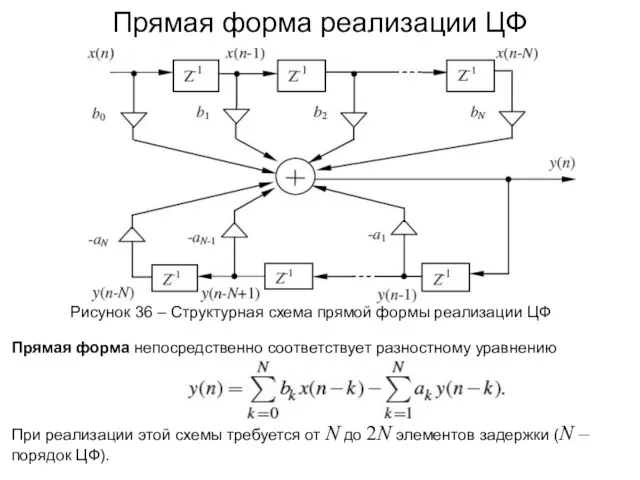
- 55. Прямая форма реализации ЦФ Рисунок 36 – Структурная схема прямой формы реализации ЦФ Прямая форма непосредственно
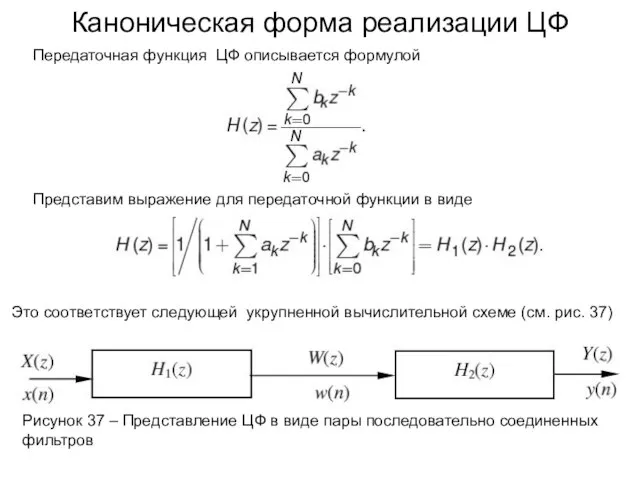
- 56. Каноническая форма реализации ЦФ Передаточная функция ЦФ описывается формулой Представим выражение для передаточной функции в виде
- 57. Каноническая форма реализации ЦФ Выполним прямое а затем обратное Z-преобразование входного x(n), выходного y(n) и «промежуточного»
- 58. Каноническая форма реализации ЦФ Рисунок 38 – Преобразованная форма ЦФ Этим формулам соответствует схема, представленная на
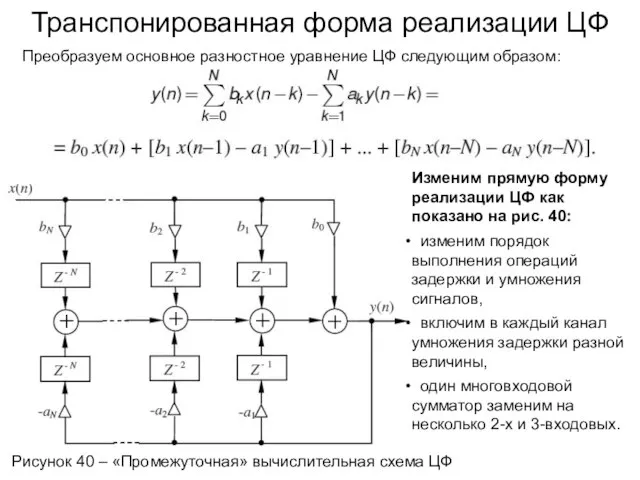
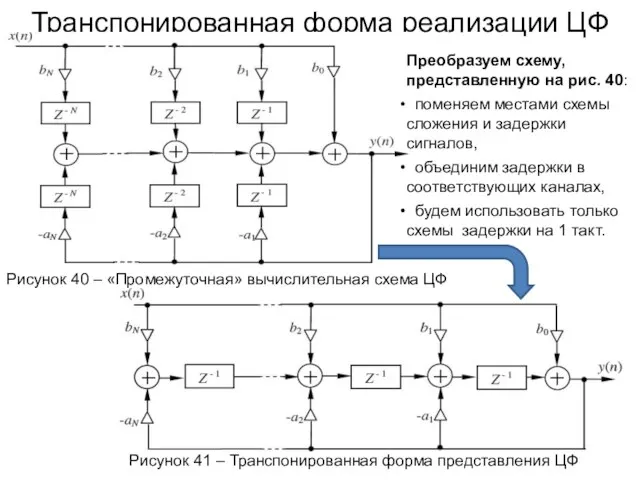
- 59. Транспонированная форма реализации ЦФ Преобразуем основное разностное уравнение ЦФ следующим образом: Изменим прямую форму реализации ЦФ
- 60. Транспонированная форма реализации ЦФ Рисунок 41 – Транспонированная форма представления ЦФ Рисунок 40 – «Промежуточная» вычислительная
- 61. Дискретные преобразования
- 62. Переход к дискретному преобразованию Фурье Выше анализировалась обработка дискретизированных во времени сигналов, имеющих непрерывный по частоте
- 63. Дискретное преобразование Фурье Для таких функций существуют прямое и обратное дискретные преобразования Фурье (ПДПФ и ОДПФ):
- 64. Дискретное преобразование Фурье Введем в этих формулах обозначение: . Тогда получим следующие формы записи для прямого
- 65. Свойства дискретного преобразования Фурье ДПФ – решетчатая функция, отсчеты которой совпадают с соответствующими значениями преобразования Фурье
- 66. 6. Связь с Z-преобразованием: По определению Подстановка дает Так можно вычислить __преобразование Фурье по результатам вычисления
- 67. Вычисление дискретного преобразования Фурье действительных последовательностей Можно вычислить ДПФ двух действительных последовательностей, применив ДПФ один раз.
- 68. Вычисление дискретного преобразования Фурье действительных последовательностей V(k)=Re[X(k)]+jIm[X(k)]+jRe[Y(k)]-Im[Y(k)] ⇒ Re [V(k)] = Re [X(k)] – Im [Y(k)],
- 69. Вычисление обратного ДПФ (ОДПФ) с помощью операции прямого ДПФ (ПДПФ) Пусть известно ДПФ X(k) последовательности x(n)
- 70. Быстрое преобразование Фурье с прореживанием во времени (алгоритм Кули-Тьюки) Дана последовательность x(n), n = 0, …,
- 71. Быстрое преобразование Фурье с прореживанием во времени Определим ДПФ от x(n): Выполнение преобразования: и подставим результат
- 72. Быстрое преобразование Фурье с прореживанием во времени X(k) определено для k = 0, …, N–1, но
- 73. Быстрое преобразование Фурье с прореживанием во времени Конечные результаты ДПФ попарно образуются из одних и тех
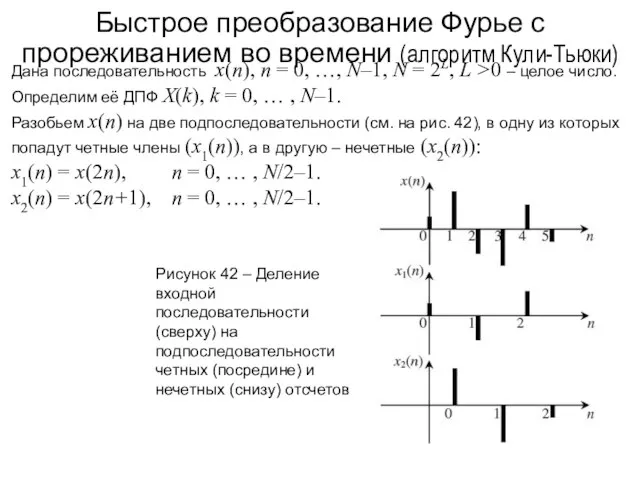
- 74. Быстрое преобразование Фурье с прореживанием во времени Дальнейшего ускорения вычислений можно достичь, осуществив аналогичное разбиение подпоследовательностей
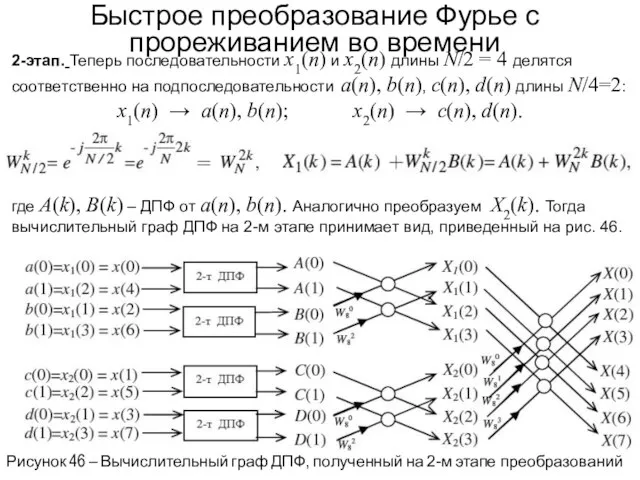
- 75. Быстрое преобразование Фурье с прореживанием во времени 2-этап. Теперь последовательности x1(n) и x2(n) длины N/2 =
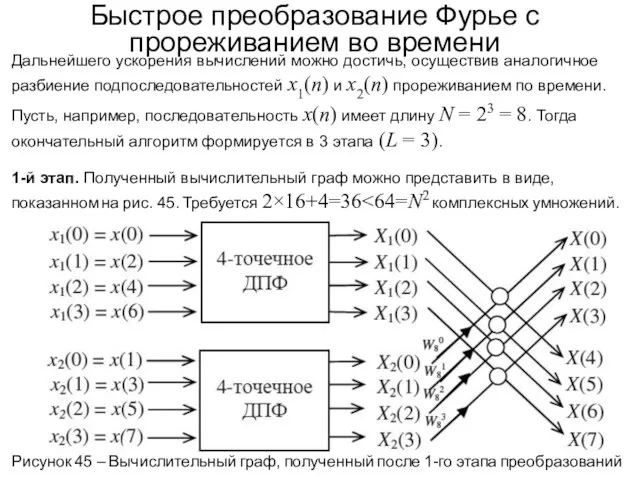
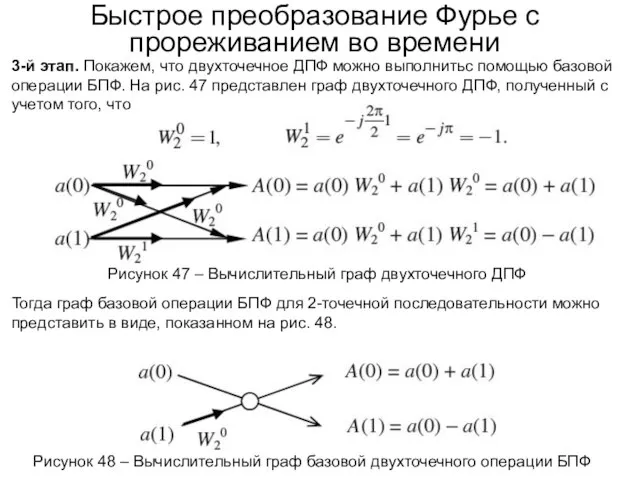
- 76. Быстрое преобразование Фурье с прореживанием во времени 3-й этап. Покажем, что двухточечное ДПФ можно выполнитьс помощью
- 77. Быстрое преобразование Фурье с прореживанием во времени Рисунок 49 – Вычислительный граф 8-точечного БПФ с прореживанием
- 78. Быстрое преобразование Фурье с прореживанием по частоте (алгоритм Кули-Тьюки) Дана последовательность x(n), n = 0, …,
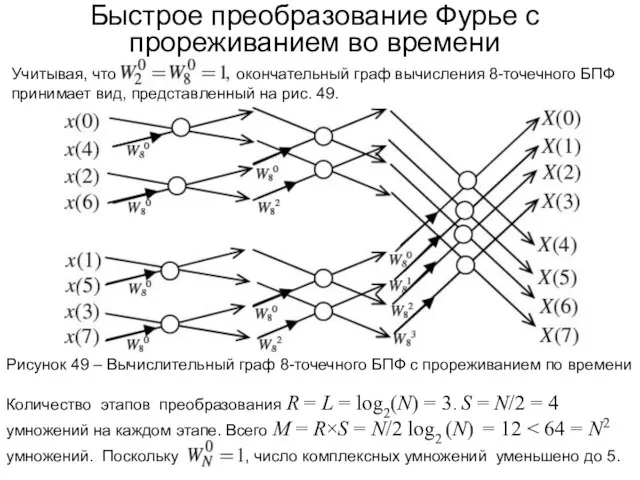
- 79. Быстрое преобразование Фурье с прореживанием по частоте По определению ДПФ от x(n) имеет вид: Далее выполняются
- 80. Быстрое преобразование Фурье с прореживанием по частоте Рисунок 52 – Вычислительный граф 8-точечного БПФ с прореживанием
- 81. Быстрое преобразование Фурье (БПФ) Для обоих алгоритмов БПФ количество комплексных умножений можно еще уменьшить, принимая во
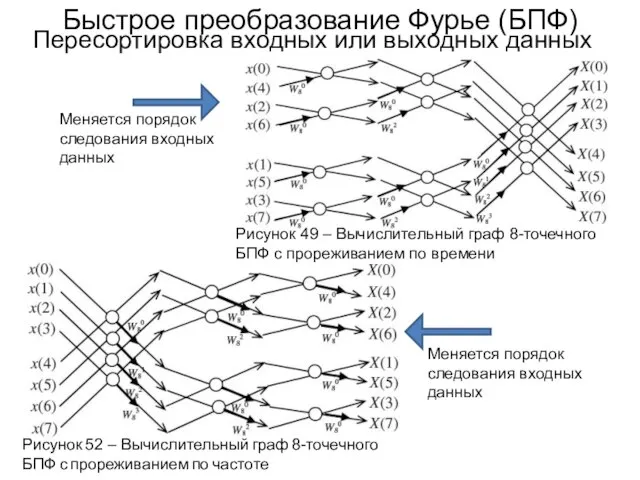
- 82. Быстрое преобразование Фурье (БПФ) Пересортировка входных или выходных данных Рисунок 52 – Вычислительный граф 8-точечного БПФ
- 83. Быстрое преобразование Фурье (БПФ) Пересортировка входных или выходных данных Пересортировка данных может быть выполнена с помощью
- 84. Единый подход к алгоритмам БПФ При вычислении БПФ мы считали длину преобразуемой последовательности N=2L, где L
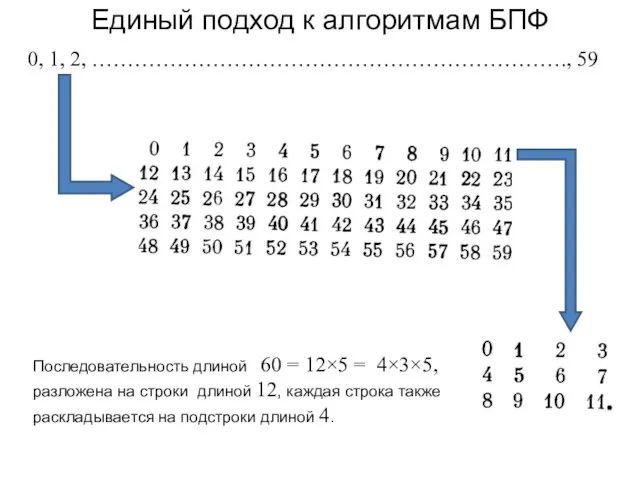
- 85. Единый подход к алгоритмам БПФ 0, 1, 2, …………………………………………………………., 59 Последовательность длиной 60 = 12×5 =
- 86. Единый подход к алгоритмам БПФ Пусть после выполнения ДПФ двумерной последовательности получим также двумерную последовательность, строки
- 87. Единый подход к алгоритмам БПФ Перемножим содержимое скобок в показателе степени в формуле (2) и учтем
- 88. Таким образом ДПФ (1) размерности N = М×L (вычислительная сложность пропорциональна N2 = М2×L2 ) было
- 89. Единый подход к алгоритмам БПФ . (3) . В формуле (3) можно изменить порядок суммирования. (4)
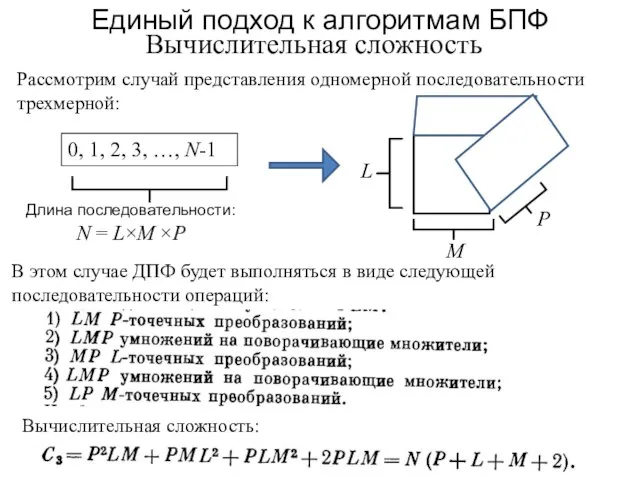
- 90. Единый подход к алгоритмам БПФ Вычислительная сложность 0, 1, 2, 3, …, N-1 Длина последовательности: N
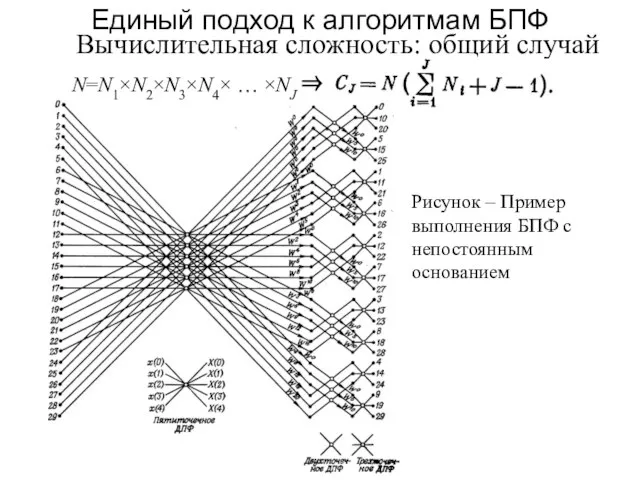
- 91. Единый подход к алгоритмам БПФ Вычислительная сложность: общий случай N=N1×N2×N3×N4× … ×NJ ⇒ Рисунок – Пример
- 92. Быстрая круговая свертка Обозначим через xp(n) и hp(n) дискретные периодические последовательности с одинаковыми периодами, равными N.
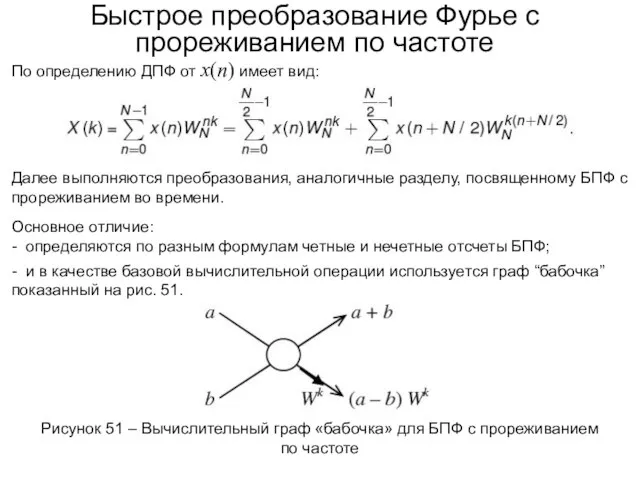
- 93. Теорема Бореля Для аналоговых сигналов теорема, сходная с теоремой о свертке была доказана с применением преобразования
- 94. Быстрая линейная (апериодическая) свертка Пусть x(n) – входной сигнал (n = 0, …, Nx–1), h(n) –
- 95. Плюсы и минусы быстрой свертки При вычислении быстрой линейной свертки операндов x длиной Nx и h
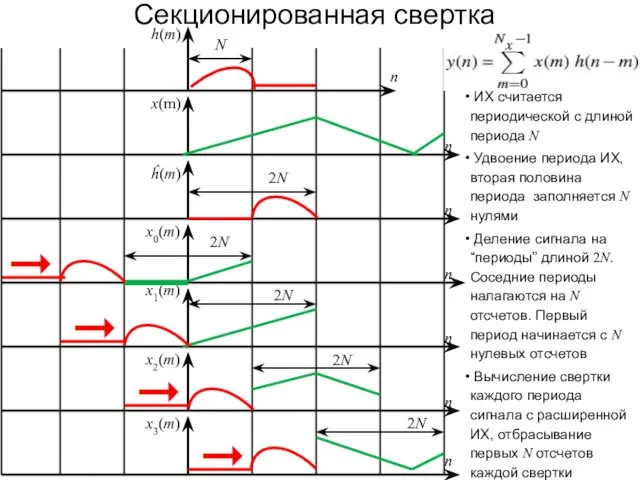
- 96. Секционированная свертка n n n n n n n x3(m) x2(m) x1(m) x0(m) ĥ(m) x(m) h(m)
- 97. Ошибки квантования
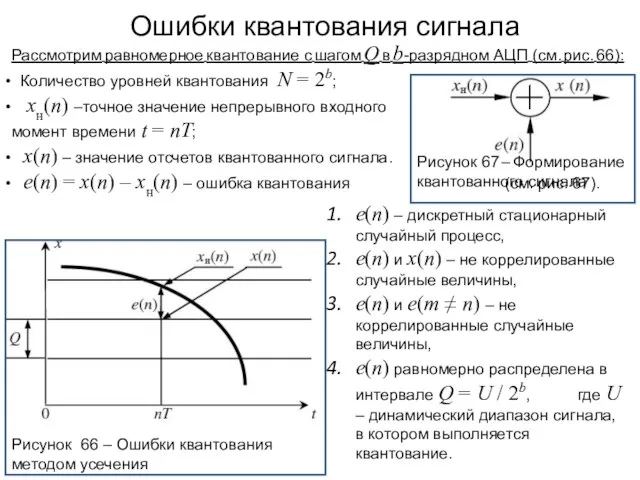
- 98. Источники и форма проявления ошибок квантования Квантование – это процесс представления чисел ограниченным числом разрядов. Рисунок
- 99. Ошибки квантования сигнала Рисунок 66 – Ошибки квантования методом усечения Рассмотрим равномерное квантование с шагом Q
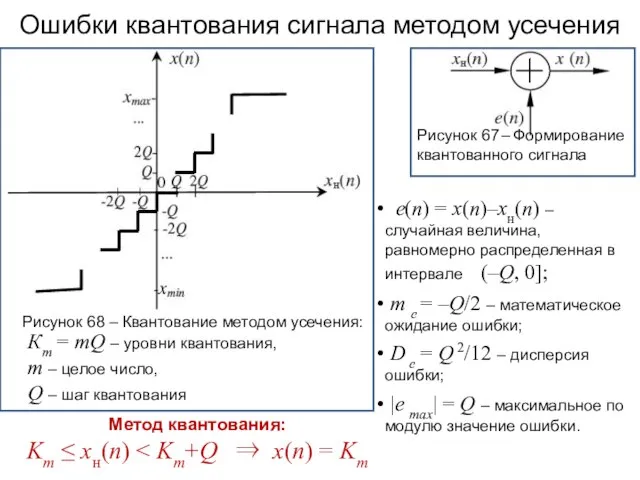
- 100. Ошибки квантования сигнала методом усечения Рисунок 68 – Квантование методом усечения: Рисунок 67 – Формирование квантованного
- 101. Ошибки квантования сигнала методом округления Рисунок 69 – Квантование методом округления Кm = mQ – уровни
- 102. Отношение сигнал/шум при квантовании Пусть гармонический сигнал с амплитудой Us квантуется b-разрядным квантователем по методу округления
- 103. Шумы квантования, приведенные к выходу ЦФ Пусть квантованный сигнал на выходе ЦФ x(n) = xн(n)+e(n), где
- 104. Пример расчета параметров шумов квантования на выходе ЦФ Определим дисперсию шумов квантования на выходе цифрового рекурсивного
- 105. Шумы квантования при выполнении арифметических операций в ЦФ Рисунок 71 – Модель ошибки квантования произведения Рассмотрим
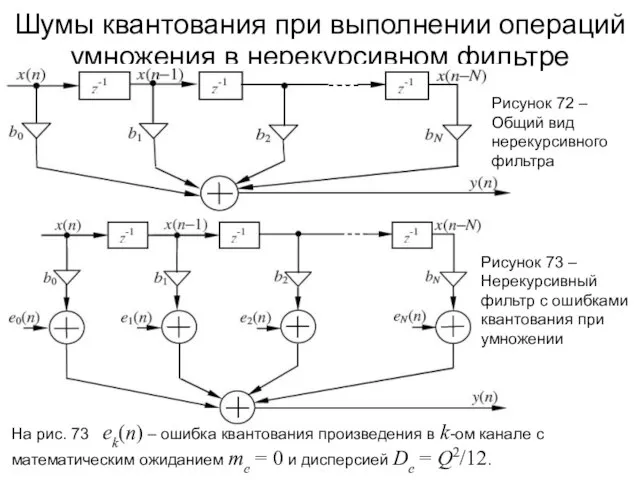
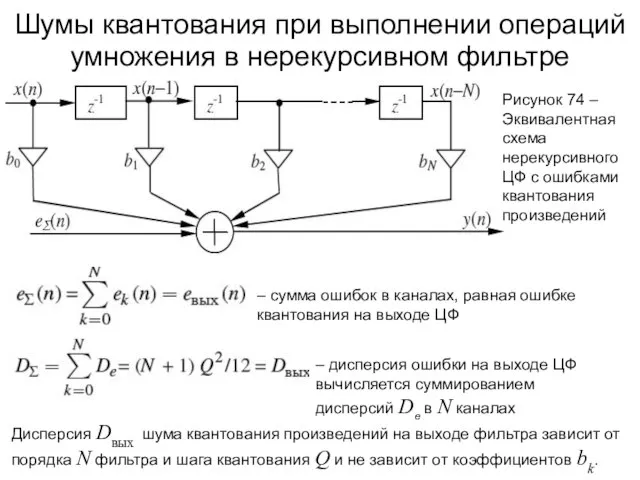
- 106. Шумы квантования при выполнении операций умножения в нерекурсивном фильтре Рисунок 72 – Общий вид нерекурсивного фильтра
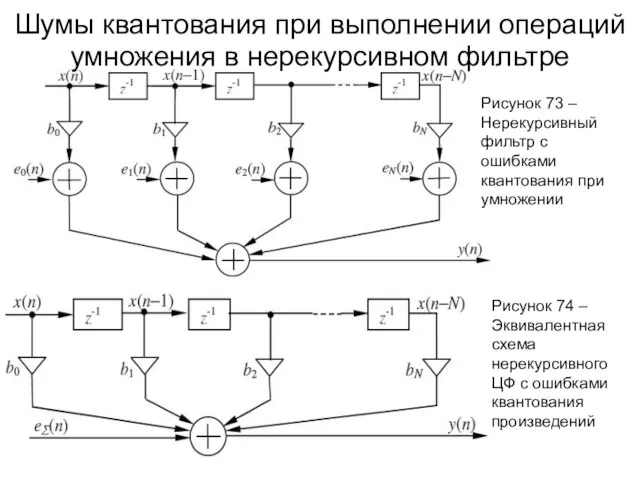
- 107. Шумы квантования при выполнении операций умножения в нерекурсивном фильтре Рисунок 73 – Нерекурсивный фильтр с ошибками
- 108. Шумы квантования при выполнении операций умножения в нерекурсивном фильтре Рисунок 74 – Эквивалентная схема нерекурсивного ЦФ
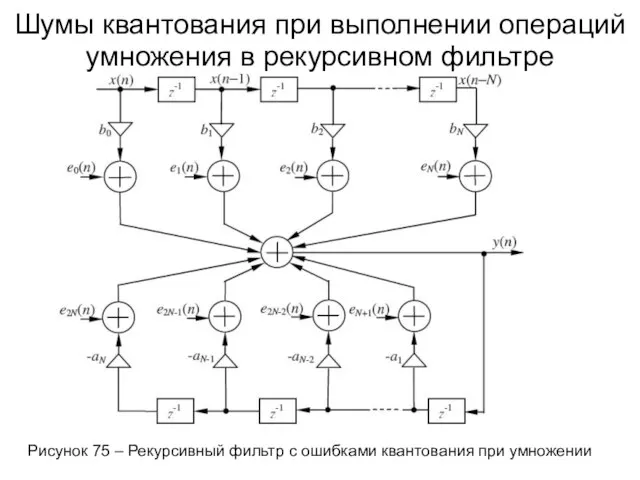
- 109. Шумы квантования при выполнении операций умножения в рекурсивном фильтре Рисунок 75 – Рекурсивный фильтр с ошибками
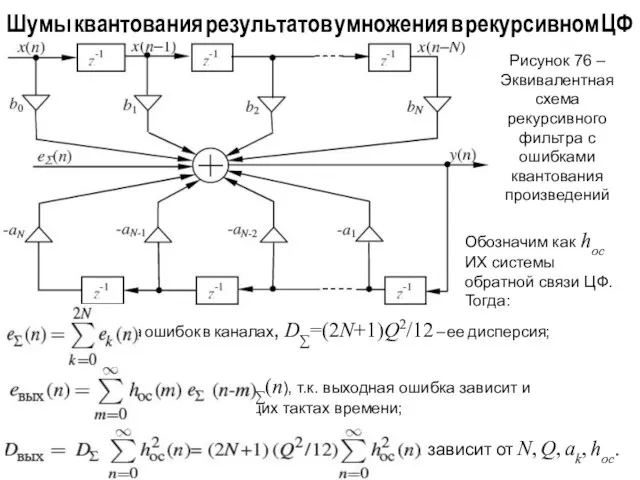
- 110. Шумы квантования результатов умножения в рекурсивном ЦФ – сумма ошибок в каналах, D∑=(2N+1)Q2/12 – ее дисперсия;
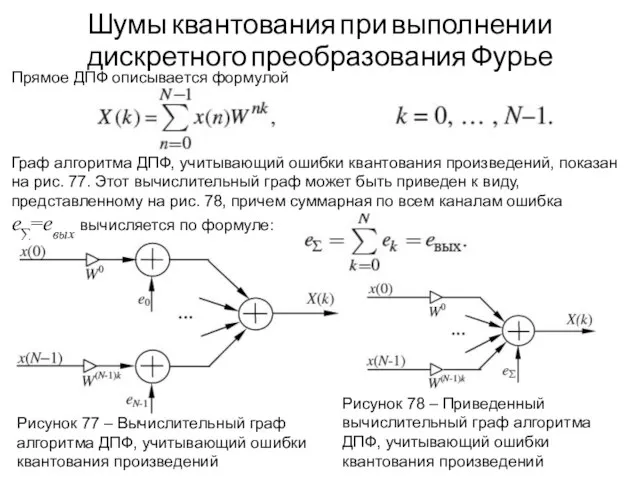
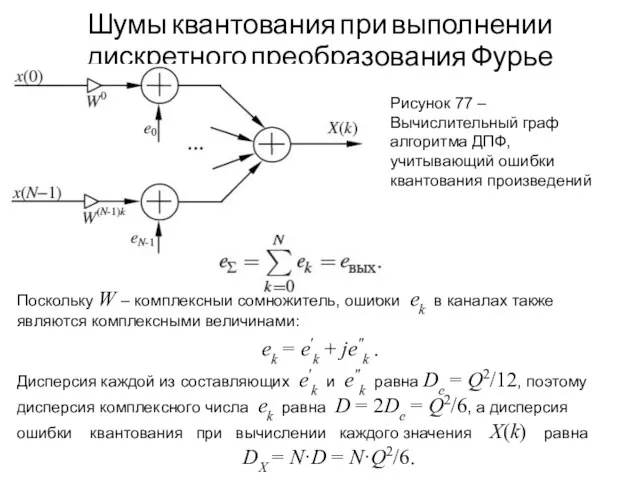
- 111. Шумы квантования при выполнении дискретного преобразования Фурье Прямое ДПФ описывается формулой Граф алгоритма ДПФ, учитывающий ошибки
- 112. Шумы квантования при выполнении дискретного преобразования Фурье Поскольку W – комплексный сомножитель, ошибки ek в каналах
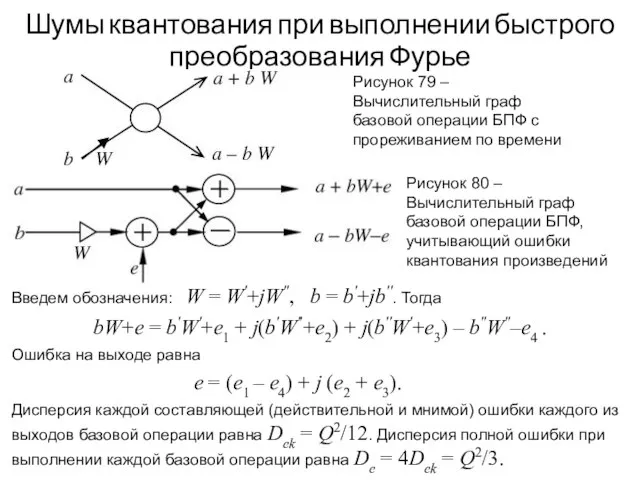
- 113. Шумы квантования при выполнении быстрого преобразования Фурье Рисунок 79 – Вычислительный граф базовой операции БПФ с
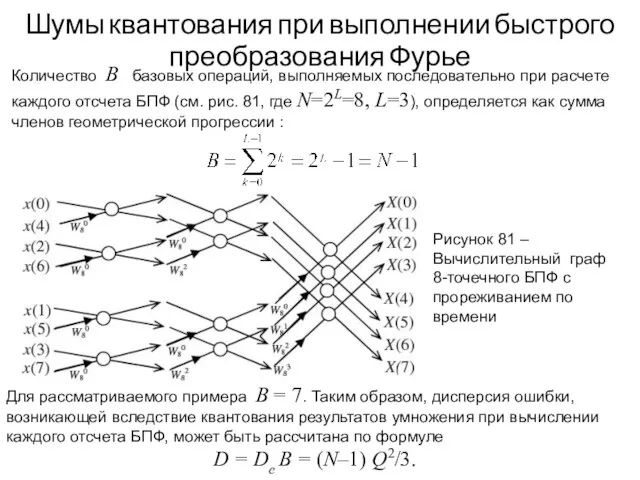
- 114. Шумы квантования при выполнении быстрого преобразования Фурье Рисунок 81 – Вычислительный граф 8-точечного БПФ с прореживанием
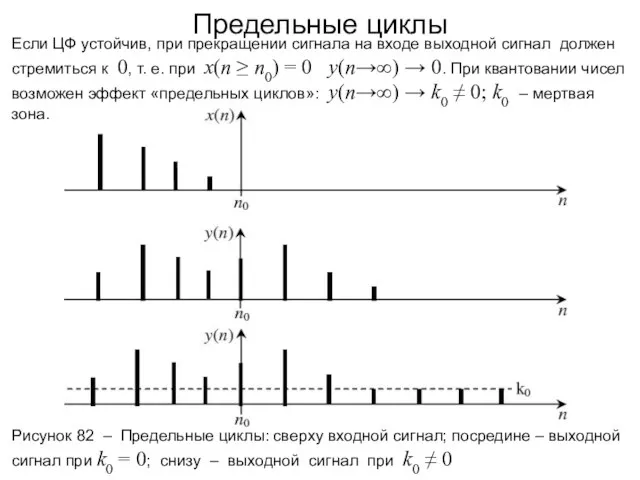
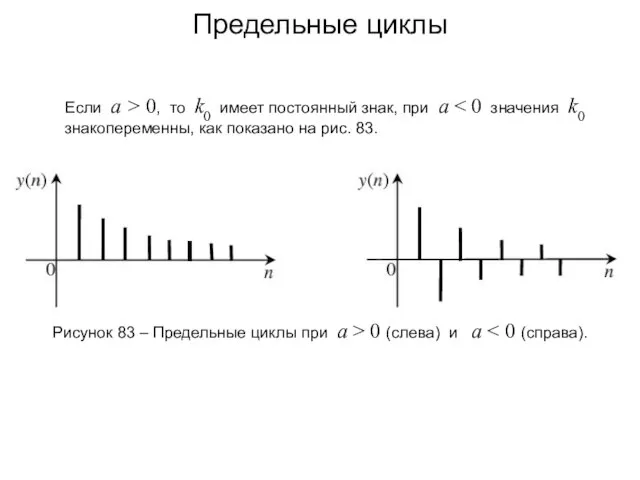
- 115. Предельные циклы Рисунок 82 – Предельные циклы: сверху входной сигнал; посредине – выходной сигнал при k0
- 116. Предельные циклы Рассмотрим пример рекурсивного фильтра 1-го порядка, описываемого разностным уравнением y(n) = x(n)+a·y(n–1), а =
- 117. Предельные циклы Если а > 0, то k0 имеет постоянный знак, при а Рисунок 83 –
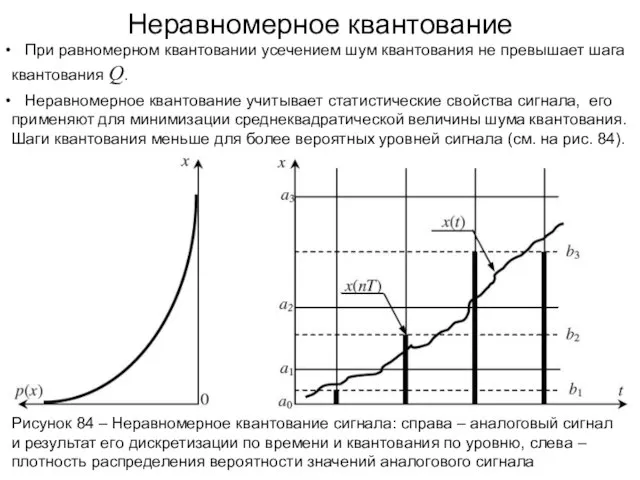
- 118. Неравномерное квантование Рисунок 84 – Неравномерное квантование сигнала: справа – аналоговый сигнал и результат его дискретизации
- 119. Неравномерное квантование В телефонии наиболее вероятны малые значения речевого сигнала, поэтому равномерное квантование потребует 12 двоичных
- 120. Спектральный анализ В контексте цифровой обработки сигналов с помощью спектрального анализа будем обнаруживать на фоне шумов
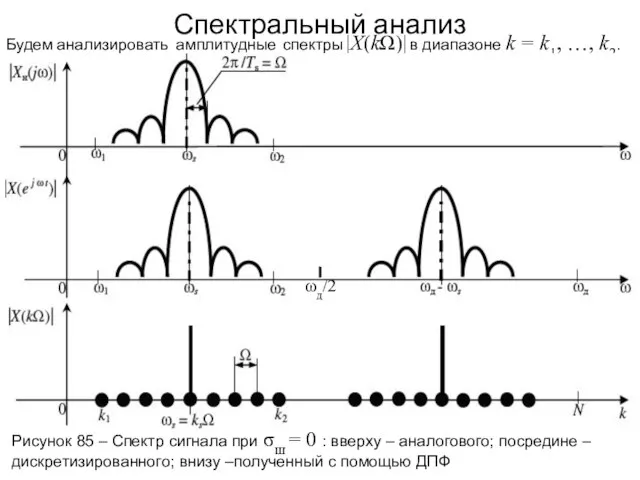
- 121. Введем следующие обозначения для спектров сигналов: Xн(jω) – спектр непрерывного сигнала xн(t), полученный преобразованием Фурье; X(e
- 122. Спектральный анализ Будем анализировать амплитудные спектры |X(kΩ)| в диапазоне k = k1, …, k2. Рисунок 85
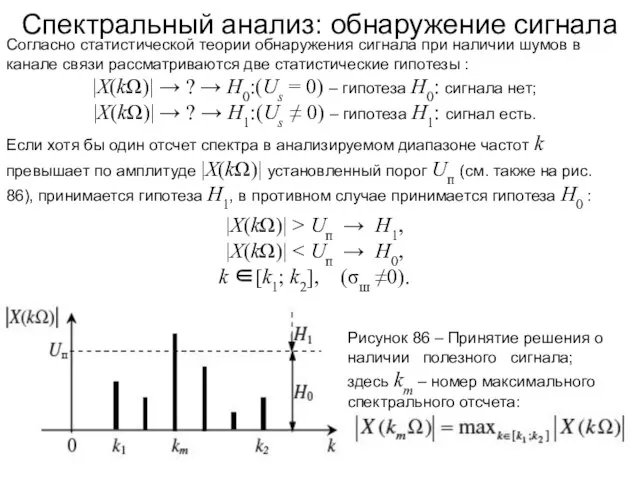
- 123. Спектральный анализ: обнаружение сигнала Согласно статистической теории обнаружения сигнала при наличии шумов в канале связи рассматриваются
- 124. Спектральный анализ: обнаружение сигнала Статистическими характеристиками обнаружителя являются: вероятность F ложной тревоги – вероятность принятия гипотезы
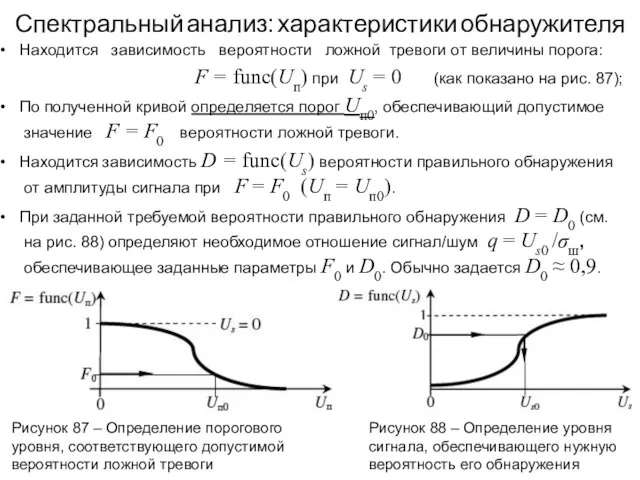
- 125. Спектральный анализ: характеристики обнаружителя Находится зависимость вероятности ложной тревоги от величины порога: F = func(Uп) при
- 126. Спектральный анализ: измерение параметров обнаруженного сигнала Измерение амплитуды Us и частоты ωs сигнала производится, только если
- 127. Ошибка измерения частоты δωs = ωs – ωs* – случайная величина, равномерно __распределенная в интервале [–Ω/2,
- 128. Расчет статистических характеристик обнаружения сигнала и измерения его параметров Для расчета статистических характеристик обнаружения и измерений
- 129. Расчет статистических характеристик обнаружения сигнала и измерения его параметров Для каждого i-того испытания, в котором обнаружен
- 130. Двумерные унитарные преобразования
- 131. Двумерные унитарные преобразования Двумерные унитарные преобразования используются для работы с двумерными массивами данных (будем рассматривать изображения)
- 132. Двумерные унитарные преобразования В результате прямого унитарного преобразования матрица изображения F(n1,n2) размерами N1×N2 преобразуется в матрицу
- 133. Двумерные унитарные преобразования Результат выполнения оператора разделимого двумерного унитарного преобразования можно находить в два этапа: Сначала
- 134. Преобразование Фурье изображения Прямое и обратное разделимые унитарные преобразования двумерных матриц Заменяем номера {n1, n2} строк
- 135. Преобразование Фурье изображения Рисунок – Частный вид ядра двумерного преобразования Фурье для пространственной частоты 2 по
- 136. Преобразование Фурье изображения Представим по формулам Эйлера комплексные экспоненты в виде сумм косинусов и синусов. Получаем
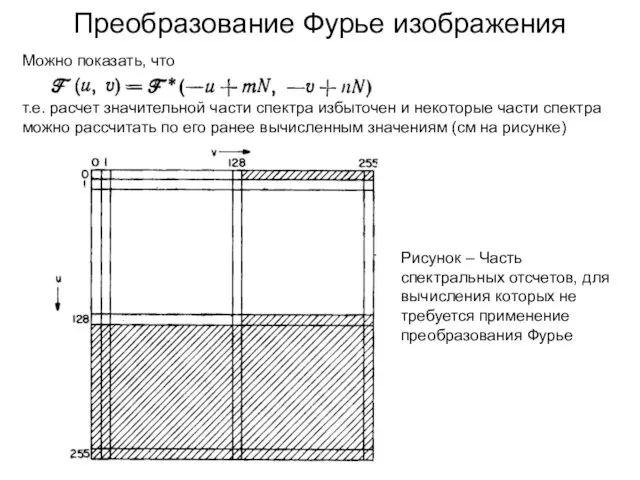
- 137. Преобразование Фурье изображения Подставив u=u+mN и v=v+nN, где m и n – постоянные, получим т.е. вычисленный
- 138. Можно показать, что , т.е. расчет значительной части спектра избыточен и некоторые части спектра можно рассчитать
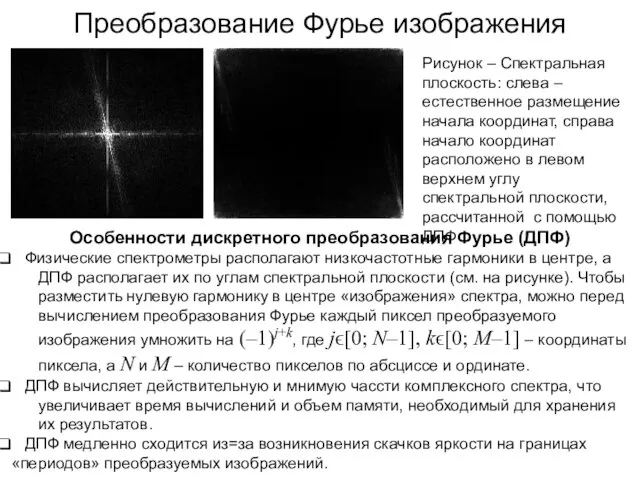
- 139. Особенности дискретного преобразования Фурье (ДПФ) Физические спектрометры располагают низкочастотные гармоники в центре, а ___ДПФ располагает их
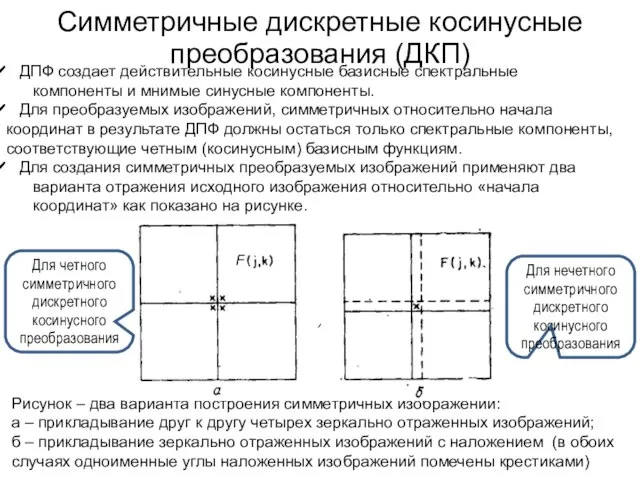
- 140. Симметричные дискретные косинусные преобразования (ДКП) ДПФ создает действительные косинусные базисные спектральные ___компоненты и мнимые синусные компоненты.
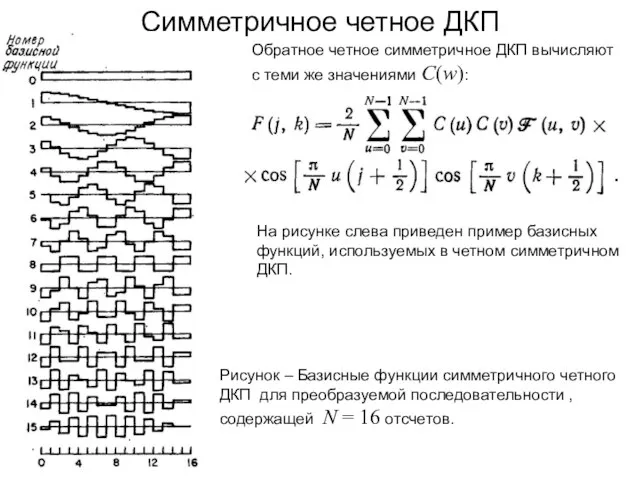
- 141. Симметричное четное ДКП Рисунок – Формирование изображения для четного ДКП где в F (j, k) номера
- 142. Симметричное четное ДКП Массив Fs(j, k) симметричен относительно начала координат и состоит из действительных чисел, следовательно,
- 143. Симметричное четное ДКП Обратное четное симметричное ДКП вычисляют с теми же значениями C(w): На рисунке слева
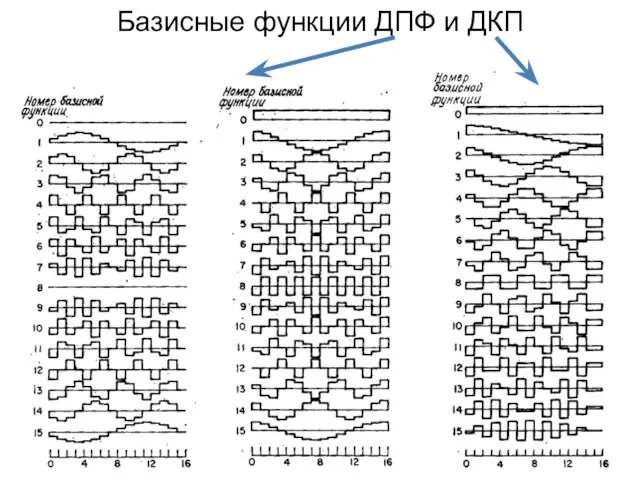
- 144. Базисные функции ДПФ и ДКП
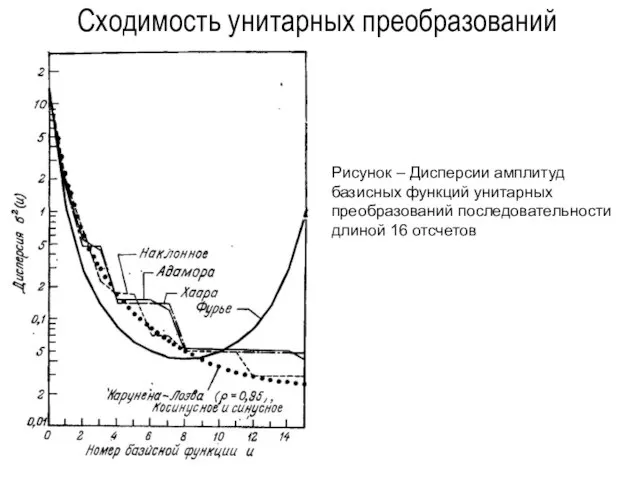
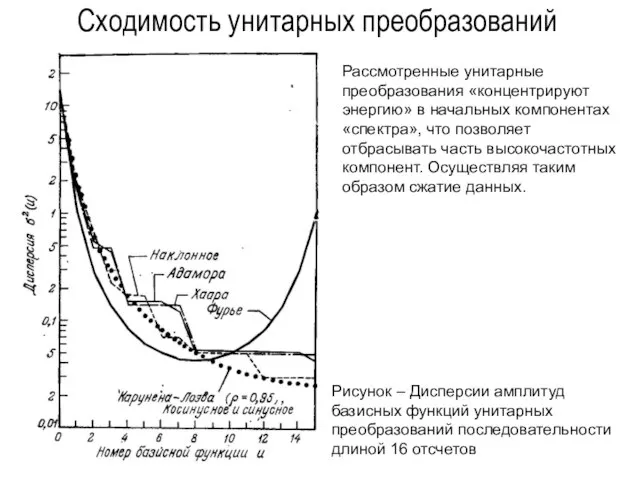
- 145. Сходимость унитарных преобразований Рисунок – Дисперсии амплитуд базисных функций унитарных преобразований последовательности длиной 16 отсчетов
- 146. Симметричное нечетное ДКП Рисунок – Формирование изображения для нечетного ДКП В соответствии с рисунком пикселы симметричного
- 147. Симметричное нечетное ДКП Поскольку преобразование Фурье обладает свойством симметрии относительно комплексного сопряжения, то для реальных изображений
- 148. Симметричное нечетное ДКП Чтобы базисные функции нечетного симметричного ДКП стали ортонормированными, вычисление производится по следующим формулам:
- 149. Симметричное нечетное ДКП Обратное преобразование Базисные функции нечетного ДКП разделимы, поэтому двумерное преобразование можно выполнить в
- 150. Дискретное синусное преобразование где j=0, …, N–1 – номера строк пикселов, а k=0, …, N–1 –
- 151. Дискретное синусное преобразование Рисунок – Базисные функции дискретного синусного преобразования для последовательности длиной 16 отсчетов
- 152. Преобразование Карунена-Лоэва C – ковариационная матрица E – математическое ожидание xk – k-тый компонент вектора mk
- 153. Преобразование Карунена-Лоэва Пусть имеется множество векторов x, заданных в N-мерном пространстве признаков. Рассчитаем для них ковариационную
- 154. Дискретное синусное преобразование Преобразование Карунена-Лоэва «поворачивает» исходный базис {x1, x2, …, xN} представления векторов так, чтобы
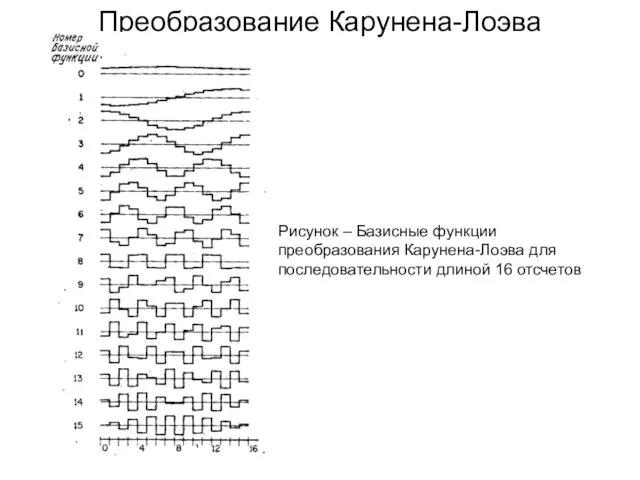
- 155. Преобразование Карунена-Лоэва Рисунок – Базисные функции преобразования Карунена-Лоэва для последовательности длиной 16 отсчетов
- 156. Разложение по негармоническим функциям
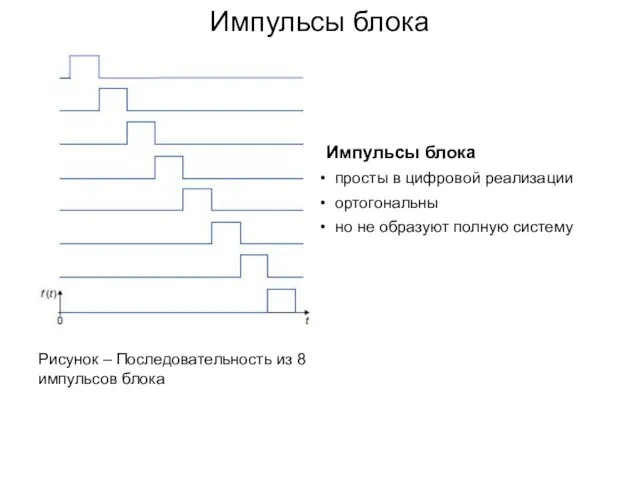
- 157. Импульсы блока Рисунок – Последовательность из 8 импульсов блока Импульсы блока просты в цифровой реализации ортогональны
- 158. Функции Уолша Рисунок – Функции Уолша для последовательности длиной 16 отсчетов Функции Уолша ортогональны образуют полную
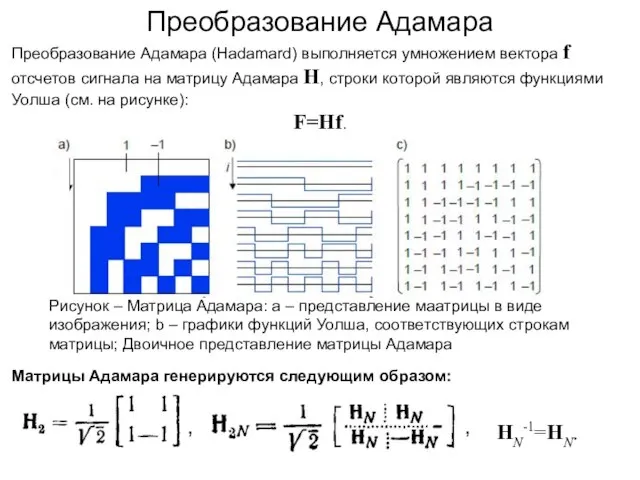
- 159. Преобразование Адамара Преобразование Адамара (Hadamard) выполняется умножением вектора f отсчетов сигнала на матрицу Адамара H, строки
- 160. Двумерное преобразование Адамара Для расчета двумерного преобразования Адамара можно сначала выполнить одномерное преобразование Адамара DWT по
- 161. Двумерное преобразование Адамара Для расчета двумерного преобразования Адамара можно сначала выполнить одномерное преобразование Адамара DWT по
- 162. Преобразование Хаара Рисунок – Базисные функции преобразования Хаара для последовательности длиной 16 отсчетов Вычисление одномерного преобразования
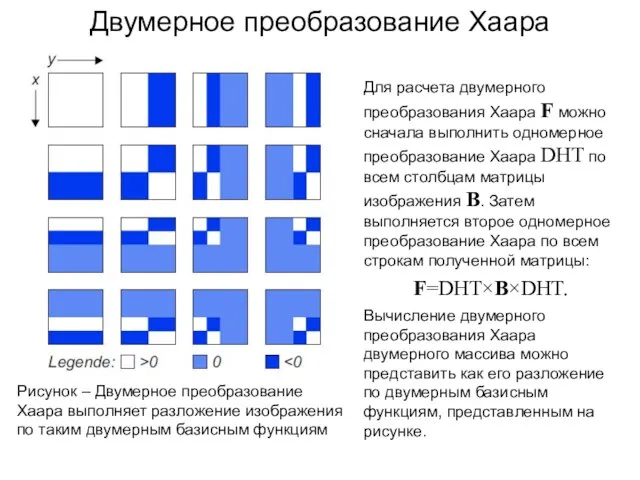
- 163. Двумерное преобразование Хаара Для расчета двумерного преобразования Хаара F можно сначала выполнить одномерное преобразование Хаара DHT
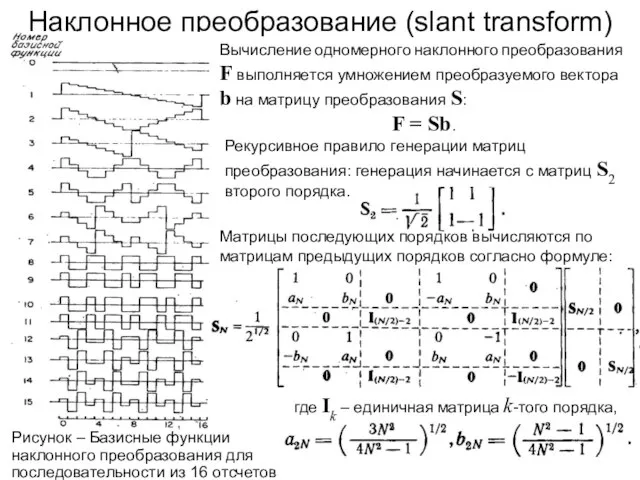
- 164. Наклонное преобразование (slant transform) Рисунок – Базисные функции наклонного преобразования для последовательности из 16 отсчетов Вычисление
- 165. Сходимость унитарных преобразований Рисунок – Дисперсии амплитуд базисных функций унитарных преобразований последовательности длиной 16 отсчетов Рассмотренные
- 166. Сингулярное преобразование
- 167. Симметричное нечетное ДКП
- 168. Симметричное нечетное ДКП
- 169. Симметричное нечетное ДКП
- 170. Симметричное нечетное ДКП
- 171. Симметричное нечетное ДКП
- 173. Скачать презентацию

























![Свойства Z-преобразования 1. Свойство линейности Если Z[x1(n)] = X1(z) и Z[x2(n)]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/524321/slide-35.jpg)



















![Вычисление дискретного преобразования Фурье действительных последовательностей V(k)=Re[X(k)]+jIm[X(k)]+jRe[Y(k)]-Im[Y(k)] ⇒ Re [V(k)] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/524321/slide-67.jpg)































































 Знакомьтесь, наш новый сотрудник
Знакомьтесь, наш новый сотрудник 20131110_prezentatsiya22
20131110_prezentatsiya22 Литье в песчаные формы
Литье в песчаные формы Система зажигания
Система зажигания Архитектор
Архитектор Modern mobile phones addiction: reasons and consequences
Modern mobile phones addiction: reasons and consequences Исследовательская работа. Роботы в нашей жизни
Исследовательская работа. Роботы в нашей жизни Наша история любви
Наша история любви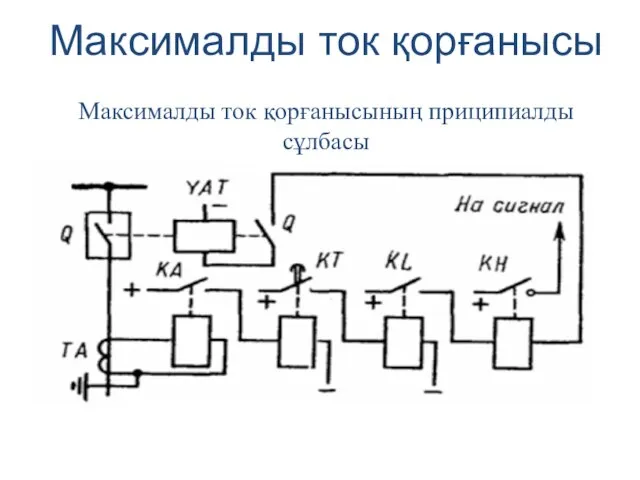 Максималды ток қорғанысы
Максималды ток қорғанысы Православные праздники
Православные праздники Экспресс-доставка грузов по России
Экспресс-доставка грузов по России Учителя первых классов на 2015-2016 учебный год
Учителя первых классов на 2015-2016 учебный год Дорожная карта
Дорожная карта Опасная ловушка
Опасная ловушка Взвейтесь кострами
Взвейтесь кострами Технологическая документация для изготовления изделий на станках
Технологическая документация для изготовления изделий на станках ЗиОБЖ_Режим питания. Ужин. Обобщение
ЗиОБЖ_Режим питания. Ужин. Обобщение Red Hot Chili Peppers
Red Hot Chili Peppers Рекомендации по подбору индивидуального стиля
Рекомендации по подбору индивидуального стиля Параллельное соединение элементов в цепи синусоидального тока
Параллельное соединение элементов в цепи синусоидального тока Македония - 2015
Македония - 2015 Моя школа вчера, сегодня, завтра
Моя школа вчера, сегодня, завтра Металургія сталі. Виробництво сталі в мартенівських печах
Металургія сталі. Виробництво сталі в мартенівських печах Основы литейного производства
Основы литейного производства Сюжетно-ролевая игра Путешествие на самолете группа Звездочка
Сюжетно-ролевая игра Путешествие на самолете группа Звездочка 20120427_urok_muzyki_3_klass
20120427_urok_muzyki_3_klass Поиск по картинке вариант 3 (3)_0_1649428572
Поиск по картинке вариант 3 (3)_0_1649428572 Упрощение выражений (подготовка к к/р)
Упрощение выражений (подготовка к к/р)