Содержание
- 4. Реализация ЦОС
- 6. 1 ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ 1.1 АНАЛОГОВЫЕ И ДИСКРЕТНЫЕ СИГНАЛЫ Сигналом называют физический процесс, несущий в себе
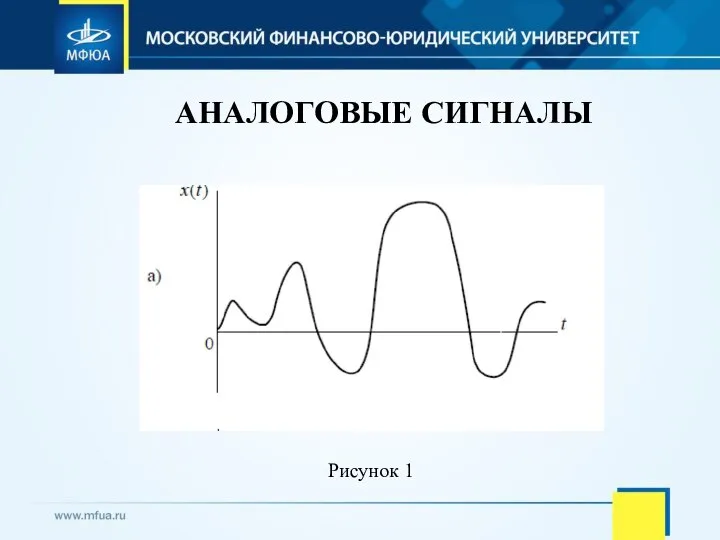
- 7. АНАЛОГОВЫЕ СИГНАЛЫ Рисунок 1
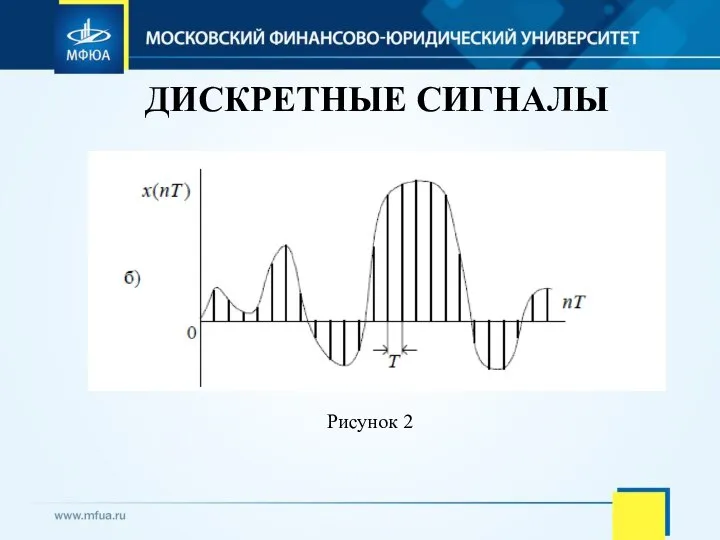
- 8. ДИСКРЕТНЫЕ СИГНАЛЫ Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию (рис. 2). Он описывается
- 9. ДИСКРЕТНЫЕ СИГНАЛЫ Рисунок 2
- 10. ЦИФРОВЫЕ СИГНАЛЫ Цифровым называют сигнал, дискретный по времени и квантованный по состоянию. Такой сигнал описывается квантованной
- 11. ЦИФРОВЫЕ СИГНАЛЫ При анализе дискретных сигналов удобно пользоваться нормированным временем (2) Таким образом, номер n отсчета
- 12. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДИСКРЕТНЫХ СИГНАЛОВ Под дискретными понимают сигналы или функции, существующие при дискретных, как правило, равноотстоящих
- 13. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДИСКРЕТНЫХ СИГНАЛОВ 2) функцией номера выборки n: x(n) = x(nTд)|Tд=1 , (5) в общем
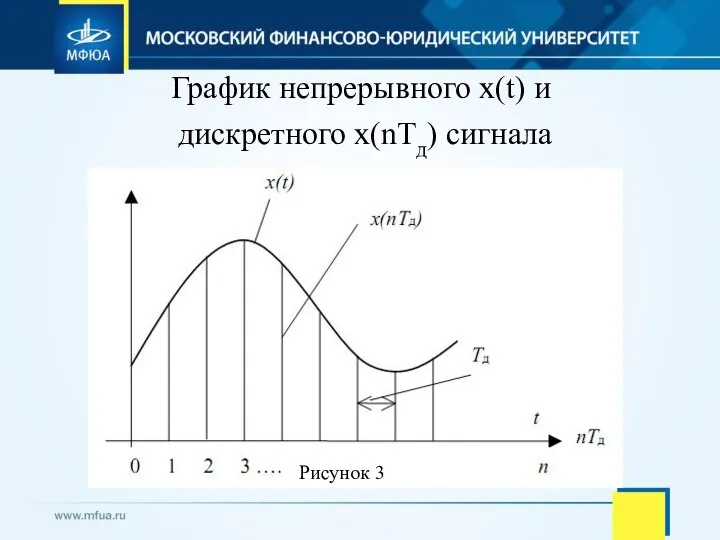
- 14. График непрерывного х(t) и дискретного х(nTд) сигнала Рисунок 3
- 15. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДИСКРЕТНЫХ СИГНАЛОВ Сигналы хд(t) и х(nТд) связаны линейным соотношением и имеют одинаковые свойства (но
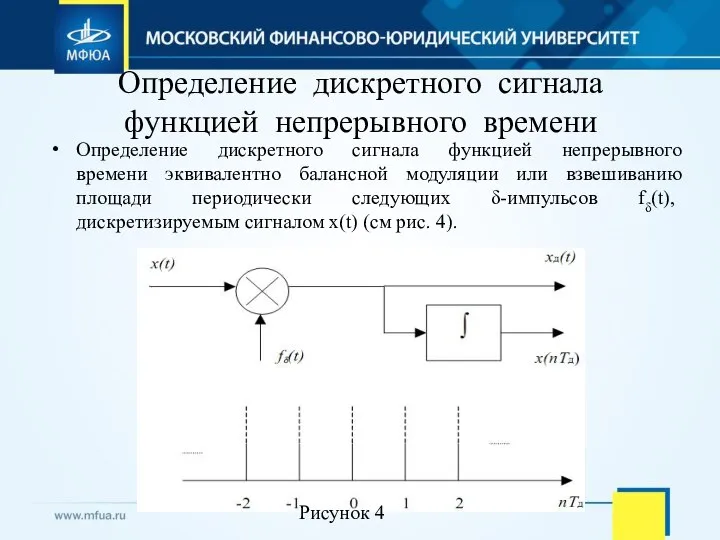
- 16. Определение дискретного сигнала функцией непрерывного времени Определение дискретного сигнала функцией непрерывного времени эквивалентно балансной модуляции или
- 17. СПЕКТР ДИСКРЕТНОГО СИГНАЛА Спектральную плотность дискретного сигнала X(jω), для упрощения называемую в дальнейшем спектром, можно найти,
- 18. СПЕКТР ДИСКРЕТНОГО СИГНАЛА С другой стороны, спектр может быть найден и прямым преобразованием Фурье дискретного сигнала,
- 19. СПЕКТР ДИСКРЕТНОГО СИГНАЛА В силу периодичности комплексной экспоненты спектр дискретного сигнала в отличие от аналогового периодичен
- 20. СВЯЗЬ МЕЖДУ СПЕКТРАМИ ДИСКРЕТНОГО И АНАЛОГОВОГО СИГНАЛОВ Связь между спектрами дискретного и аналогового сигналов получается на
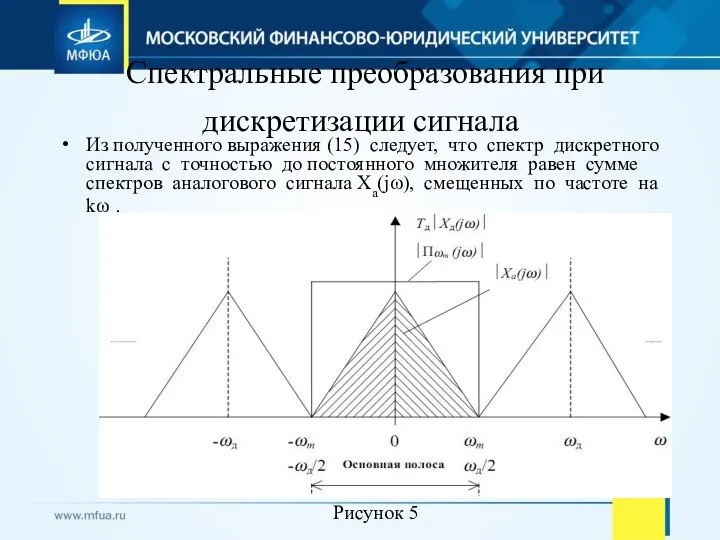
- 21. Спектральные преобразования при дискретизации сигнала Из полученного выражения (15) следует, что спектр дискретного сигнала с точностью
- 22. Теорема Котельникова Теоре́ма Коте́льникова (в англоязычной литературе — теорема Найквиста — Шеннона или теорема отсчётов) гласит:
- 23. Теорема Котельникова Сигнал на выходе ФНЧ соответствует обратному преобразованию Фурье депериодизированного спектра дискретного сигнала Выражение (18)
- 24. Наложение спектров при дискретизации Частота, определяемая как ωд/2 = ωm, носит известное по зарубежной литературе название
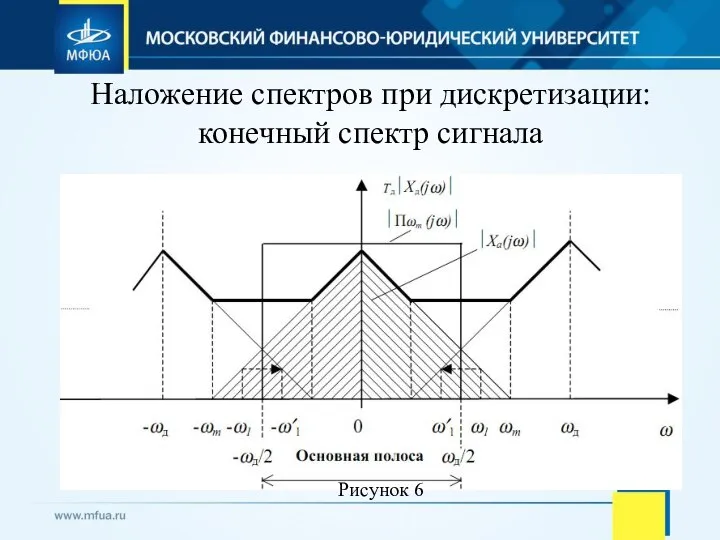
- 25. Наложение спектров при дискретизации: конечный спектр сигнала Рисунок 6
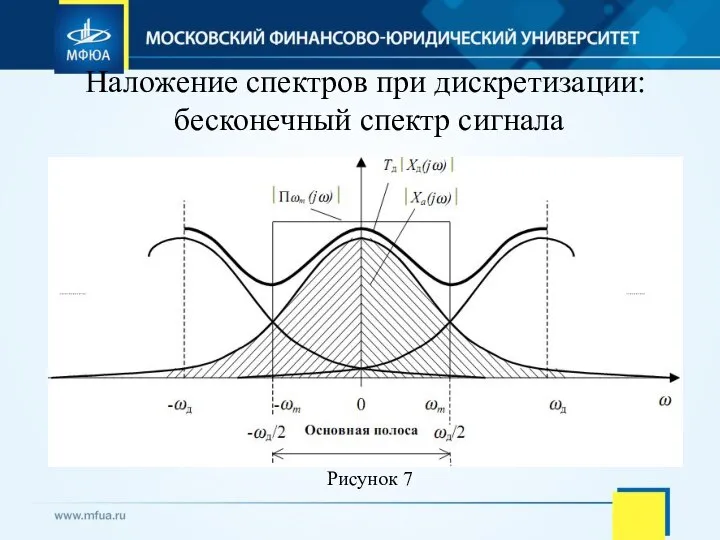
- 26. Наложение спектров при дискретизации: бесконечный спектр сигнала Рисунок 7
- 27. Подмена частот С наложением спектров при дискретизации реальных сигналов связано также явление подмены или маскирования частот,
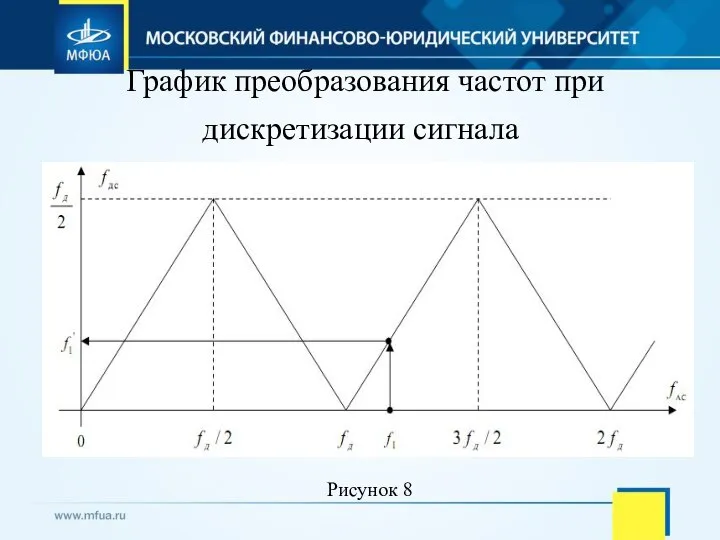
- 28. График преобразования частот при дискретизации сигнала Рисунок 8
- 30. Скачать презентацию



















 Методики испытаний высоковольтных выключателей
Методики испытаний высоковольтных выключателей Угадай мелодию по смайлам
Угадай мелодию по смайлам Filozofe středověku 1. -15. století
Filozofe středověku 1. -15. století Арки. Общая характеристика. Схемы арок, конструкция и расчет
Арки. Общая характеристика. Схемы арок, конструкция и расчет Тарифное регулирование гарантирующего поставщика: формирование и составляющие тарифа на электрическую энергию для населения
Тарифное регулирование гарантирующего поставщика: формирование и составляющие тарифа на электрическую энергию для населения Сюжетно-ролевая игра Путешествие на самолете группа Звездочка
Сюжетно-ролевая игра Путешествие на самолете группа Звездочка 肯德基
肯德基 Принципы организации каналов связи для управления БЛА
Принципы организации каналов связи для управления БЛА Строение ткани: ткацкие переплетения
Строение ткани: ткацкие переплетения Материалы для дистанционной поддержки учащихся по дополнительной программе Юный художник
Материалы для дистанционной поддержки учащихся по дополнительной программе Юный художник презентация Блокада Ленинграда
презентация Блокада Ленинграда المَرافِق العامّة1
المَرافِق العامّة1 Слайды пропусков последняя версия.pptx
Слайды пропусков последняя версия.pptx Дипломная работа для семинара итоговый вариант
Дипломная работа для семинара итоговый вариант История компании Самсунг
История компании Самсунг Документы, сопровождающие процесс Внутреннего аудита. Регламентирующие документы
Документы, сопровождающие процесс Внутреннего аудита. Регламентирующие документы Илья Жаворонков
Илья Жаворонков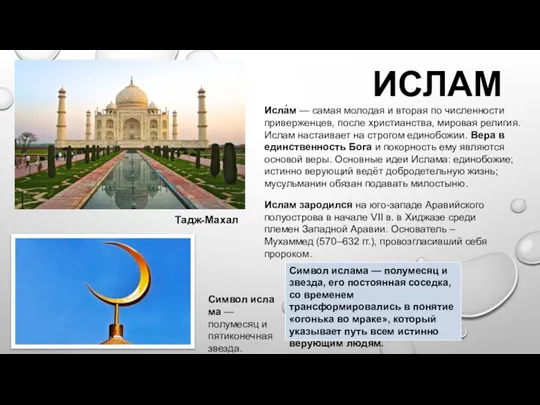 Ислам. Тадж-Махал
Ислам. Тадж-Махал Речной вокзал
Речной вокзал Обучение РТП
Обучение РТП Типовые схемы автоматических сборочных агрегатов для автоматической и полуавтоматической сборки цилиндрических соединений
Типовые схемы автоматических сборочных агрегатов для автоматической и полуавтоматической сборки цилиндрических соединений АНАГРАММЫ
АНАГРАММЫ 100 к 1
100 к 1 20141222_den_konstitutsii
20141222_den_konstitutsii 20150402_9_maja2
20150402_9_maja2 ООО_Завод_среднего_машиностоения_презентация_2
ООО_Завод_среднего_машиностоения_презентация_2 Lavy
Lavy Конкурс фотографий Памятные места родного края
Конкурс фотографий Памятные места родного края