Содержание
- 2. Турчак Л.Е. Основы численных методов. Учебное пособие. – М.:Наука. – 2003. – 320 с. Тарасевич. Основы
- 3. Область применения численных методов – решение тех задач математического анализа, для которых аналитическое (точное) решение затруднено
- 4. Аналитические Теоретические рассуждения и выводы. Рассматриваются в курсе математики, физики и др. наук. Конечный результат: Формулы,
- 5. Графические Построение графиков, диаграмм, запись измерений с помощью датчиков. Конечный результат: Графики и точки на графиках.
- 6. Численные Решение задачи сводится к вычислению в определенной последовательности. Конечный результат: Число или числа. Преимущества: Решение
- 7. Численные методы позволяют свести решение задачи к выполнению конечного числа арифметических действий над числами, при этом
- 8. 1. Вычисления с помощью ручки и бумаги можно проводить с любой степенью точности 2. В компьютере
- 9. Постановка задачи (исходные данные и определение конечного результата исследования). Построение модели (модель должна адекватно описывать законы
- 10. Опр. Нелинейным называется уравнение, которое содержит неизвестное Xn (n≠1) или переменная X входит под знак функции.
- 11. 1. Локализация корня X0, т.е. нахождение интервала (a,b), где X0∈(a,b), в котором содержится корень уравнения. 2.
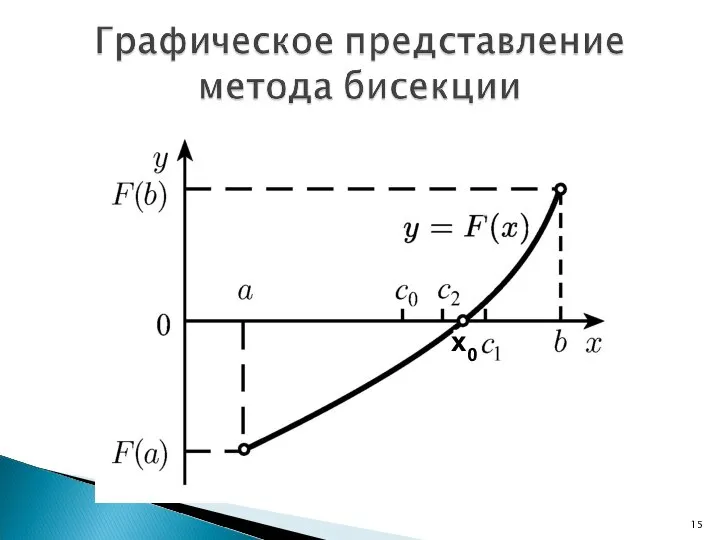
- 12. Постановка задачи: Решить уравнение f(x)=0. Пусть на интервале [a,b] содержится один корень уравнения x0. На данном
- 13. Тогда, чтобы найти корень уравнения X0 необходимо сделать следующее: 1. Найти середину отрезка [a,b], точку c=(a+b)/2.
- 14. 5. Переопределить интервал: новый интервал поиска снова назвать как [a,b]. 6. Проверить, достигнута ли заданная точность
- 16. 1. Локализация корня. Составим таблицу значений функции f(x)=-x4+5: Из таблицы видно, что корень находится на интервале
- 17. 1 итерация a:= 1 b:= 2 c:=(a+b)/2 c=1.5 f(b)*f(c) = 0.688 > 0 поэтому b:=c |b-a|=0.5
- 18. 1. Метод бисекции (деление отрезка пополам); 2. Метод хорд (метод касательных); 3. Метод итераций (метод последовательных
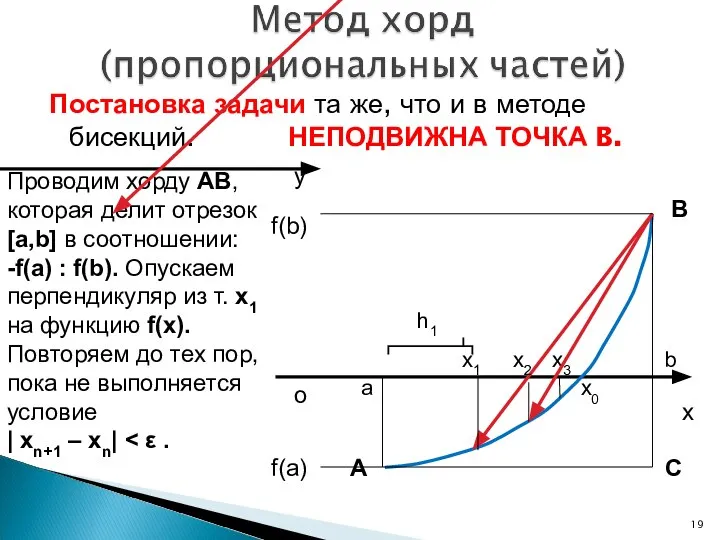
- 19. Постановка задачи та же, что и в методе бисекций. НЕПОДВИЖНА ТОЧКА B. Проводим хорду AB, которая
- 20. Неподвижна та граница интервала, для которой знак функции f(x) совпадает со знаком ее второй производной f
- 21. Из подобия треугольников ΔAax1 и ΔABC следует: Тогда длина отрезка h1 равна: ? Случай используется, если
- 22. Найдем значение в т. x1: Тогда последовательно находим следующие точки: и т.д. Окончательно получаем: (*)
- 23. НЕПОДВИЖНА ТОЧКА А. Проводим хорду AB, которая делит отрезок [a,b] в соотношении: f(b) : -f(a). Опускаем
- 24. Из подобия треугольников ΔBbx1 и ΔABC следует: Тогда длина отрезка h1 равна: ? Случай используется, если
- 25. Найдем значение в т. x1: Тогда последовательно находим следующие точки: и т.д. Окончательно получаем: (**)
- 26. Метод хорд заключается в том, что на отрезке [a,b] функция f(x) заменяется стягивающей её хордой. В
- 27. В матричном виде система уравнений записывается в виде: Здесь aij – матрица коэффициентов при неизвестных; Bj
- 29. Скачать презентацию










![Постановка задачи: Решить уравнение f(x)=0. Пусть на интервале [a,b] содержится один](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1303140/slide-11.jpg)

![5. Переопределить интервал: новый интервал поиска снова назвать как [a,b]. 6.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1303140/slide-13.jpg)






![НЕПОДВИЖНА ТОЧКА А. Проводим хорду AB, которая делит отрезок [a,b] в](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1303140/slide-22.jpg)


![Метод хорд заключается в том, что на отрезке [a,b] функция f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1303140/slide-25.jpg)

 Начертательная геометрия. Точка и линия на поверхности. Пересечение поверхностей. Сфера. Тор. Конус
Начертательная геометрия. Точка и линия на поверхности. Пересечение поверхностей. Сфера. Тор. Конус Ip - домофония от компании Дом.ru
Ip - домофония от компании Дом.ru Лютеранство (евангелическое христианство)
Лютеранство (евангелическое христианство) Рассказ в экскурсии
Рассказ в экскурсии Система стандартов разработки и постановки продукции на производство (СРПП)
Система стандартов разработки и постановки продукции на производство (СРПП) Принципы международного права
Принципы международного права Гражданское право. Тема 8
Гражданское право. Тема 8 Современные политические системы; сущность и особенности Выполнили Белова А Майданюк Е
Современные политические системы; сущность и особенности Выполнили Белова А Майданюк Е Пословицы и поговорки мира
Пословицы и поговорки мира Типы и виды тестирования по доступу к исходному коду
Типы и виды тестирования по доступу к исходному коду Big picture. Persistence
Big picture. Persistence Циклы в Паскале
Циклы в Паскале Фонд Социального Страхования
Фонд Социального Страхования Бруцеллез
Бруцеллез ТестТП2сем_закл2вопр
ТестТП2сем_закл2вопр  ПРИЧИНЫ РАЗВИТИЯ СНИЖАЮЩЕГОСЯ ПРИКУСА
ПРИЧИНЫ РАЗВИТИЯ СНИЖАЮЩЕГОСЯ ПРИКУСА  Рокотов Фёдор Степанович (1735 — 1808)
Рокотов Фёдор Степанович (1735 — 1808) Романовская игрушка
Романовская игрушка Тема 2. Социально – экономические предпосылки возникновения новой социальной группы – предпринимателей.
Тема 2. Социально – экономические предпосылки возникновения новой социальной группы – предпринимателей.  Город Чайковский. Удивительная рыба ООО «Акела»
Город Чайковский. Удивительная рыба ООО «Акела» Пристрої введення і виведення інформації
Пристрої введення і виведення інформації Германо- скадинавская мифология
Германо- скадинавская мифология Микроэкономика Основные вопросы темы: Основы теории потребительского поведения 1. Полезность: общая и предельная 2.  
Микроэкономика Основные вопросы темы: Основы теории потребительского поведения 1. Полезность: общая и предельная 2.   Инженерная и компьютерная графика
Инженерная и компьютерная графика Паровая и газовая турбины
Паровая и газовая турбины Урок-по-духовному-краеведению-Что-такое-религиозная-культура
Урок-по-духовному-краеведению-Что-такое-религиозная-культура Презентация на тему "Динамічні групи" - скачать презентации по Педагогике
Презентация на тему "Динамічні групи" - скачать презентации по Педагогике Искусство первобытного человека
Искусство первобытного человека