Содержание
- 2. Повторение материала
- 3. Универсальным называется множество U, состоящее из всех возможных элементов, обладающих данным признаком. Если множество не содержит
- 4. Множество, элементами которого являются подмножества множества М, называется семейством множества М или булеаном этого множества и
- 5. Множество считается заданным, если перечислены все его элементы, или указано свойство, которым обладают те и только
- 6. Примеры задания множества Множество всех чисел, являющихся неотрицательными степенями числа 2 можно задать: а) перечислением элементов:
- 7. 1.2. Основные операции над множествами Суммой или объединением двух множеств Х и Y называется множество, состоящее
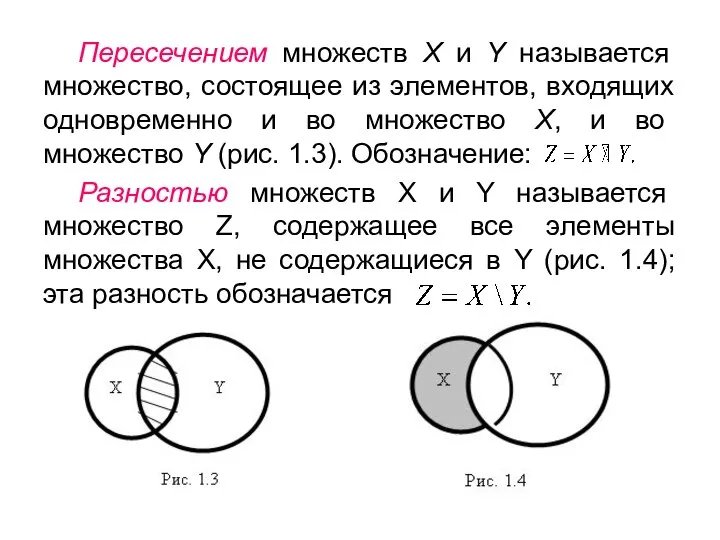
- 8. Пересечением множеств Х и Y называется множество, состоящее из элементов, входящих одновременно и во множество Х,
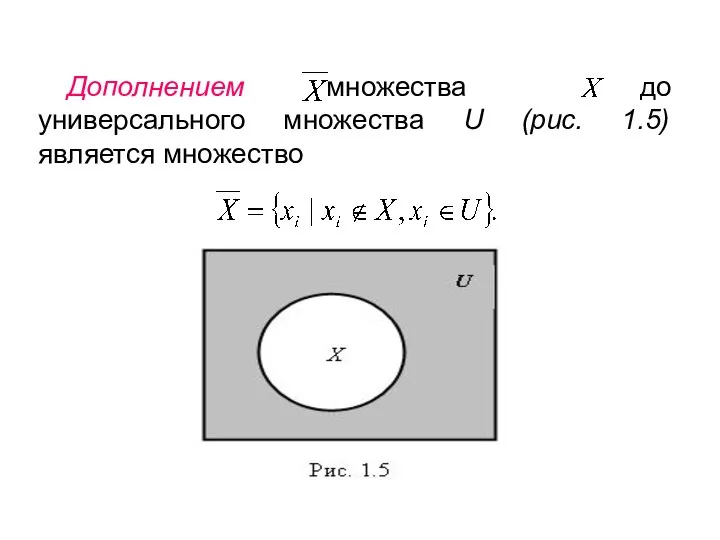
- 9. Дополнением множества до универсального множества U (рис. 1.5) является множество
- 10. Симметрической разностью множеств X и Y называется множество Z, содержащее либо элементы множества X, либо элементы
- 11. Вместо выражения «любое х из множества Х» можно писать , где перевёрнутая латинская буква А взята
- 12. Множество A можно разбить на классы (непересекающиеся подмножества) Ai, если: объединение всех подмножеств совпадает с множеством
- 13. Для операций над множествами справедливы следующие тождества: законы коммутативности объединения и пересечения законы ассоциативности объединения и
- 14. законы дистрибутивности пересечения относительно объединения и объединения относительно пересечения законы поглощения законы склеивания законы Порецкого Операция
- 15. законы идемпотентности объединения и пересечения законы действия с универсальным (U) и пустым ( ∅ ) множествами
- 16. План Декартово произведение множеств. Отношения. Бинарные отношения и их свойства. Соответствие между множествами.
- 17. В начальных классах ученики решают задачу: используя цифры 1, 2, 3 образовать всевозможные двузначные числа. Путем
- 18. Запись каждого числа состоит из двух цифр, причем существенен порядок их следования. Например, из цифр 1,
- 19. Рассмотрим другой пример. Пусть А={1, 2, 3}, B={4, 5}. Образуем всевозможные пары (а;b) Получим некоторое новое
- 20. Декартовым произведением множеств А и В называется множество пар, первые элементы которых принадлежат множеству А, вторые
- 21. Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.
- 22. Рассмотрим следующий пример. Известно, что АXВ={(2, 3), (2, 5), (2, 6), (3, 3), (3, 5), (3,
- 23. Количество пар в декартовом произведении АXВ будет равно произведению числа элементов множества А и числа элементов
- 24. В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов.
- 25. Декартовым произведением множеств А1, А2, …, Аn называют множество кортежей длины n, образованных так, что первый
- 26. 2. Понятие соответствия АхВ: Соответствие — это множество всех пар, в котором первый элемент принадлежит А,
- 27. Проекция: AxBxCx...xM Если число сомножеств равно n, то это множество векторов длины n, в котором 1-й
- 28. Соответствие Соответствием называется некое подмножество прямого произведения АхВ
- 29. Пары задают соответствие между множествами A и B, если указано правило R, по которому для элемента
- 30. Образ множества A при соответствии R называется множеством значений этого соответствия и обозначается , если состоит
- 31. Для описания соответствий между множествами используют понятие отображения. Для задания отображения f необходимо указать: множество, которое
- 32. При записи подразумевается, что отображение f определено всюду на A, т.е. A – полный прообраз отображения
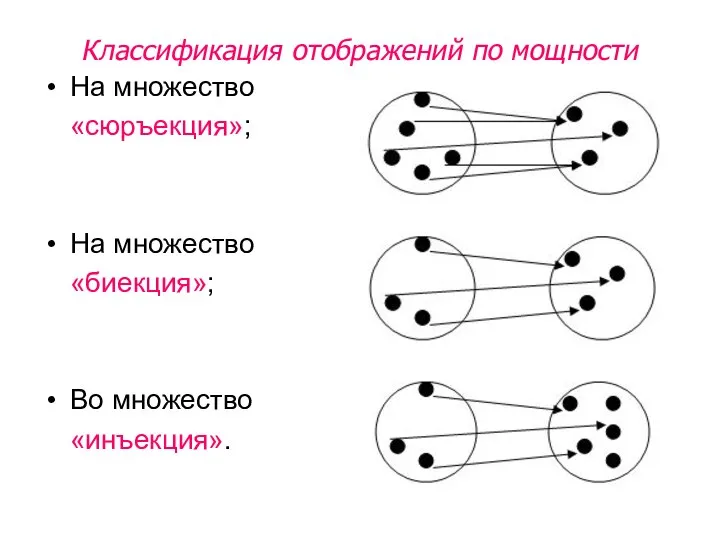
- 33. Классификация отображений по мощности На множество «сюръекция»; На множество «биекция»; Во множество «инъекция».
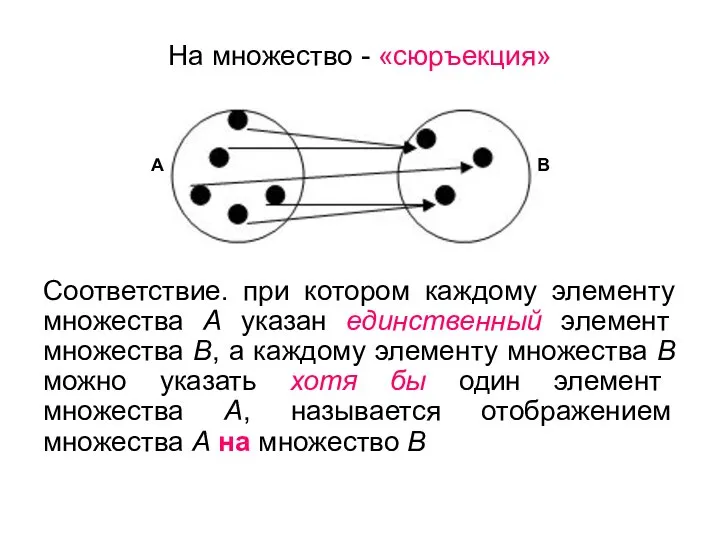
- 34. На множество - «сюръекция» Соответствие. при котором каждому элементу множества А указан единственный элемент множества В,
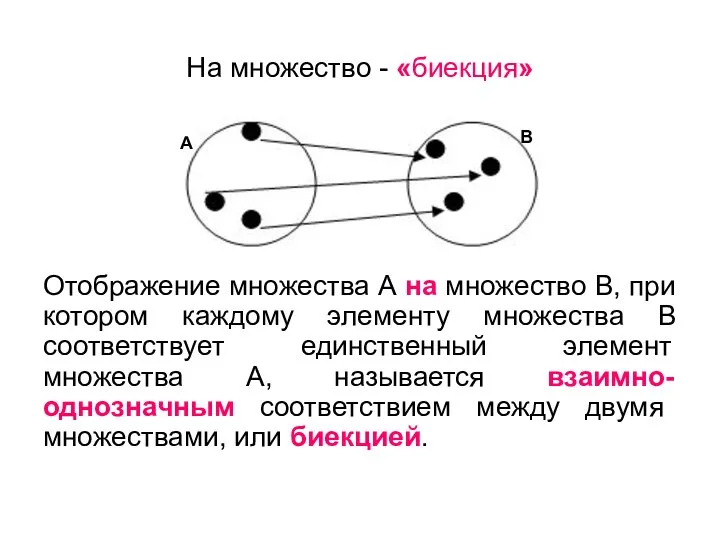
- 35. На множество - «биекция» Отображение множества А на множество В, при котором каждому элементу множества В
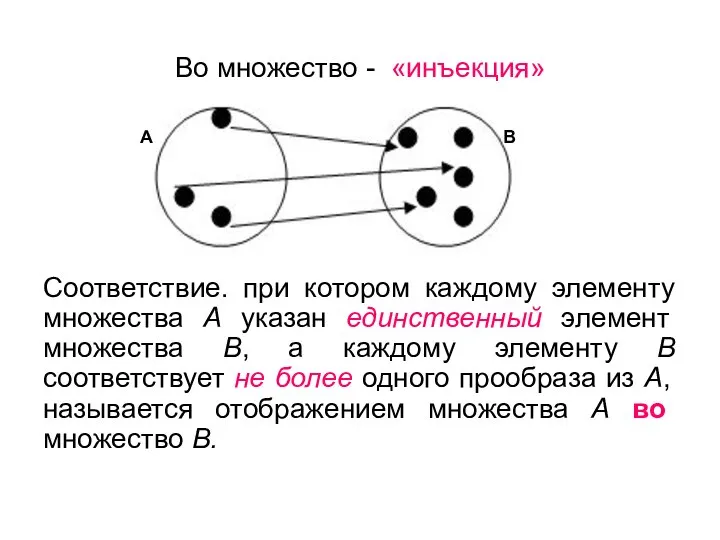
- 36. Во множество - «инъекция» Соответствие. при котором каждому элементу множества А указан единственный элемент множества В,
- 37. Пусть множество А отображается взаимно-однозначно на множество В, т.е. . Тогда отображение , при котором каждому
- 38. Кортежем длины n из элементов множества А называется упорядоченная последовательность элементов этого множества. Кортежи и называются
- 39. В отличие от элементов множества элементы кортежа могут совпадать. Например, в прямоугольной системе координат координаты точек
- 40. Существуют кортежи, элементы которых являются только нулями или единицами. Кортеж из нулей и единиц можно рассматривать
- 41. Декартовым (прямым) произведением множеств называется множество , состоящее из всех кортежей длины n, в которых ,
- 42. Отношения. Бинарные отношения и их свойства Подмножество называется n-местным отношением R на непустом множестве М. При
- 43. симметричность: антисимметричность: асимметричность:
- 44. транзитивность: антитранзитивность: связность: или
- 45. Каждое конкретное отношение может обладать или не обладать указанным свойством. Примеры рефлексивных отношений: «быть не больше»;
- 46. Примеры антисимметричных отношений: «быть меньше или равным»; «быть делителем»; «быть подмножеством»; Примеры асимметричных отношений; «быть больше»;
- 47. Примеры отношений связности: «быть больше», «быть меньше» на множестве N, R; «быть больше или равным», «быть
- 48. Непересекающиеся подмножества, на которые разбивается множество М отношением эквивалентности, называются классами эквивалентности. На множестве обыкновенных дробей
- 49. Отношение эквивалентности – частный случай отношения толерантности. Отношения «быть другом», «быть знакомым», - отношения толерантности, так
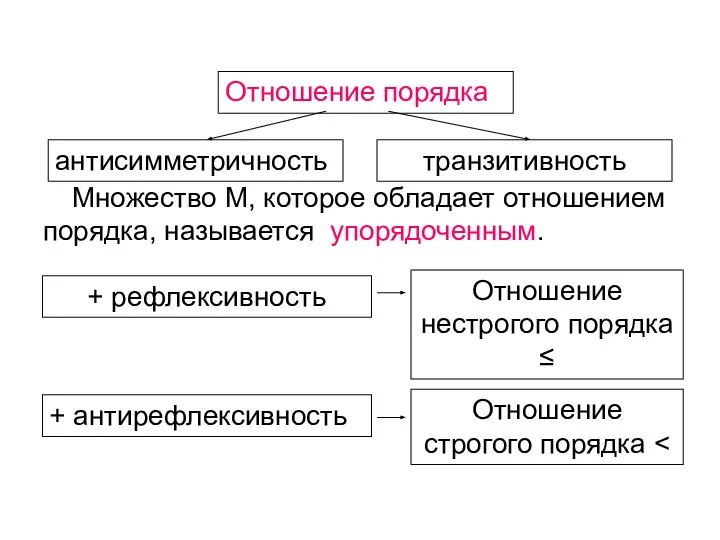
- 50. Множество М, которое обладает отношением порядка, называется упорядоченным. Отношение порядка антисимметричность транзитивность + рефлексивность + антирефлексивность
- 52. Скачать презентацию



































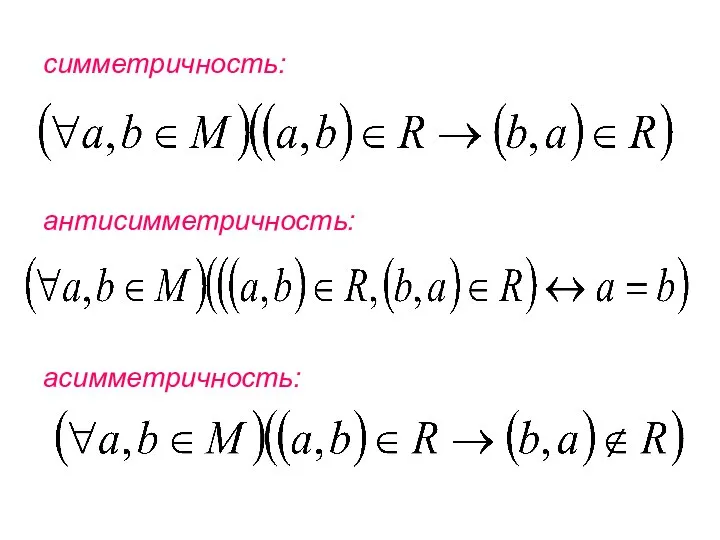
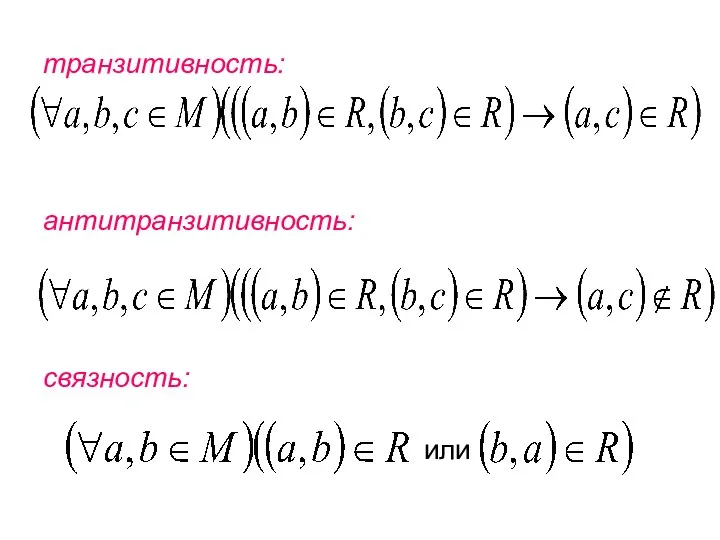





 Связи с общественностью в условиях кризиса
Связи с общественностью в условиях кризиса ГУ-ВШЭ кафедра финансового учета и финансовой отчетности Лукьянов Павел Андреевич plukyanov@hotmail.com
ГУ-ВШЭ кафедра финансового учета и финансовой отчетности Лукьянов Павел Андреевич plukyanov@hotmail.com  Техники тест-дизайна. Планирование, оценка трудозатрат. Отчетность. Лекция 5
Техники тест-дизайна. Планирование, оценка трудозатрат. Отчетность. Лекция 5 Дисциплина профессионального цикла для студентов, обучающихся по магистерским программам
Дисциплина профессионального цикла для студентов, обучающихся по магистерским программам  Месопотамия
Месопотамия Кинжал в Египте (5 класс)
Кинжал в Египте (5 класс) Сцепление автомобиля Камаз-4310
Сцепление автомобиля Камаз-4310 Хвойные ростения
Хвойные ростения Геохронология
Геохронология Политическая элита и политическое лидерство
Политическая элита и политическое лидерство Один текст- разные заголовки - презентация для начальной школы
Один текст- разные заголовки - презентация для начальной школы Презентация на тему "Базы данных 14" - скачать презентации по Медицине
Презентация на тему "Базы данных 14" - скачать презентации по Медицине Методы и приемы агитационной работы
Методы и приемы агитационной работы Презентация "Наука и хозяйство" - скачать презентации по Экономике
Презентация "Наука и хозяйство" - скачать презентации по Экономике буква ш - презентация для начальной школы
буква ш - презентация для начальной школы Коран и Сунна - священные книги мусульман
Коран и Сунна - священные книги мусульман Полицейские города Череповца, погибшие при исполнении воинского долга
Полицейские города Череповца, погибшие при исполнении воинского долга Дом мечты
Дом мечты Горицкий воскресенский женский монастырь
Горицкий воскресенский женский монастырь Презентация на тему "Домашние задания. Как научить ребёнка стать самостоятельным?" - скачать презентации по Педагогике
Презентация на тему "Домашние задания. Как научить ребёнка стать самостоятельным?" - скачать презентации по Педагогике Формы и содержание взаимодействия инструктора по физической культуре с семьями воспитанников ДОО
Формы и содержание взаимодействия инструктора по физической культуре с семьями воспитанников ДОО Органы государственной власти
Органы государственной власти Создание системы защиты ИСПДн «Работники» ООО «Металлобаза»
Создание системы защиты ИСПДн «Работники» ООО «Металлобаза» Эйвон. Инструкция по отправке заказа
Эйвон. Инструкция по отправке заказа Моделирование работы электромагнитного акустического преобразователя
Моделирование работы электромагнитного акустического преобразователя Использование ультразвукового дальномера на Arduino для нахождения роботом пути выхода из лабиринта
Использование ультразвукового дальномера на Arduino для нахождения роботом пути выхода из лабиринта Международные экологические конференции и организации
Международные экологические конференции и организации Спортивный клуб КНИТУ-КАИ им. Туполева
Спортивный клуб КНИТУ-КАИ им. Туполева