Содержание
- 2. Замена переменных в двойном интеграле Заменим переменные x и y : Если функции x и y
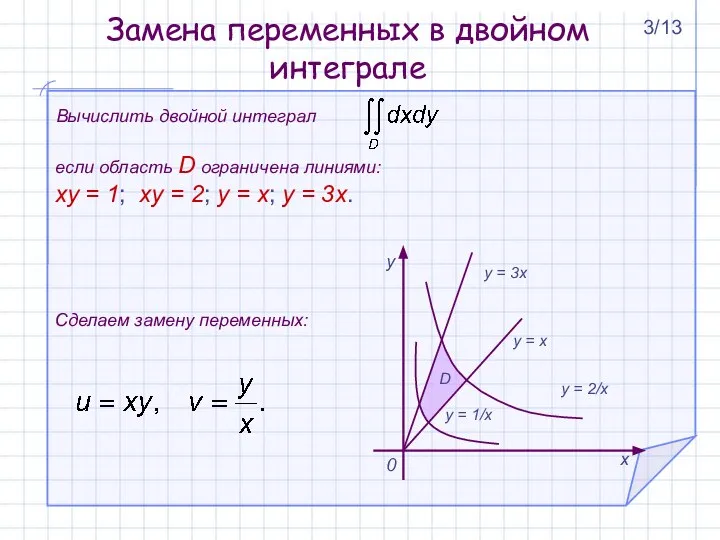
- 3. Замена переменных в двойном интеграле Вычислить двойной интеграл если область D ограничена линиями: xy = 1;
- 4. Найдем уравнения линий, ограничивающих область D* Замена переменных в двойном интеграле 4/13
- 5. Выразим переменные x и y через u и v. Найдем частные производные от получившихся функций: Замена
- 6. Найдем якобиан преобразования: Замена переменных в двойном интеграле 6/13
- 7. D* Построим область D*. Расставим пределы интегрирования, пользуясь формулой (1): Вычислим двукратный интеграл: Замена переменных в
- 8. Двойной интеграл в полярных координатах Рассмотрим частный случай замены переменных: замену декартовых координат x и y
- 9. Формула замены переменных принимает вид: Двойной интеграл в полярных координатах Область в полярной системе координат, соответствующая
- 10. Расставим пределы интегрирования: Внутренний интеграл здесь берется при постоянном φ. Двойной интеграл в полярных координатах D*
- 11. Замечания 1 2 Переход к полярным координатам целесообразен, когда подынтегральная функция имеет вид f(x2+y2) ; область
- 12. Вычислить Перейдем к полярным координатам: Двойной интеграл в полярных координатах Изобразим область D в декартовой системе
- 14. Скачать презентацию










 Директивы в Angular
Директивы в Angular מבוא לג'אווהסקריפט
מבוא לג'אווהסקריפט Социально-политические взгляды Томаса Гоббса, Джона Локка, Луи Монтескье, Вольтера, Дени Дидро
Социально-политические взгляды Томаса Гоббса, Джона Локка, Луи Монтескье, Вольтера, Дени Дидро Азаматтық құқығы
Азаматтық құқығы Презентация на тему "САХАРНЫЙ ДИАБЕТ И ПРИЧИНЫ ЕГО РАЗВИТИЯ" - скачать презентации по Медицине
Презентация на тему "САХАРНЫЙ ДИАБЕТ И ПРИЧИНЫ ЕГО РАЗВИТИЯ" - скачать презентации по Медицине Классификация и виды моделей систем Статистическое моделирование
Классификация и виды моделей систем Статистическое моделирование Обычаи, обряды и традиции русского народа
Обычаи, обряды и традиции русского народа Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании "Северодвинск&quo
Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании "Северодвинск&quo Патофизиология воспаления
Патофизиология воспаления Белорусы - восточнославянский народ
Белорусы - восточнославянский народ Организация психолого-медико-педагогического сопровождения воспитанников с особыми образовательными потребностями в условиях Д
Организация психолого-медико-педагогического сопровождения воспитанников с особыми образовательными потребностями в условиях Д Thanksgiving day
Thanksgiving day Инфекционный мононуклеоз
Инфекционный мононуклеоз Свобода совести. Религиозное верование
Свобода совести. Религиозное верование Метро. История метро
Метро. История метро Учитель МБОУ «Средняя общеобразовательная школа №2» г. Мензелинска Республики Татарстан Петрова С.С. Технологический профиль
Учитель МБОУ «Средняя общеобразовательная школа №2» г. Мензелинска Республики Татарстан Петрова С.С. Технологический профиль Корпоративные сети
Корпоративные сети Сколько весит мой ранец? Работу выполнила: Щербакова Наталья,
Сколько весит мой ранец? Работу выполнила: Щербакова Наталья,  Аппараты вспомогательной цепи
Аппараты вспомогательной цепи Становление философских систем в эпоху античности
Становление философских систем в эпоху античности Марушка Надія Іванівна
Марушка Надія Іванівна Начертательная геометрия. Инженерная графика
Начертательная геометрия. Инженерная графика Понятие и виды юридической ответственности
Понятие и виды юридической ответственности Сертификация авиационной техники. Понятия и принципы технического регулирования
Сертификация авиационной техники. Понятия и принципы технического регулирования Специялен проект представен от елина ангелова НАДЯВАМ СЕ ДА ВИ ХАРЕСА ТОВА Е ЗА ВСИЧКИ ХОРА КОИТО СИ ТЪРСЯТ ПОДХОДЯЩИЯТ ТИП КУХН
Специялен проект представен от елина ангелова НАДЯВАМ СЕ ДА ВИ ХАРЕСА ТОВА Е ЗА ВСИЧКИ ХОРА КОИТО СИ ТЪРСЯТ ПОДХОДЯЩИЯТ ТИП КУХН Теорема о пополнении. Лебеговы пространства.
Теорема о пополнении. Лебеговы пространства. 3,4анатомия.ткани
3,4анатомия.ткани Методы пропаганды и способы ее разоблачения
Методы пропаганды и способы ее разоблачения