Содержание
- 2. 1. Уравнения Максвелла и волновое уравнение. Рассмотрим однородную и изотропную, электрически нейтральную, непроводящую среду. Электромагнитное поле
- 3. 1. Уравнения Максвелла и волновое уравнение. Вычислим ротор от правой и левой части уравнения (1). В
- 4. 1. Уравнения Максвелла и волновое уравнение. После вычисления ротора от левой части уравнения (1) получаем: Согласно
- 5. 1. Уравнения Максвелла и волновое уравнение. После вычисления ротора от правой и левой части уравнения (1)
- 6. 1. Уравнения Максвелла и волновое уравнение. Сравним полученное уравнение с общим видом дифференциального волнового уравнения: где
- 7. 1. Уравнения Максвелла и волновое уравнение. Решениями волнового уравнения для вектора напряжённости электрического поля также являются
- 8. 1. Уравнения Максвелла и волновое уравнение. Вычислим ротор от правой и левой части уравнения (3). Аналогично
- 9. 1. Уравнения Максвелла и волновое уравнение. Это уравнение можно переписать так: где - фазовая скорость волны.
- 10. 1. Уравнения Максвелла и волновое уравнение. Фазовая скорость электромагнитной волны В вакууме, когда ε = 1
- 11. 1. Уравнения Максвелла и волновое уравнение. Основные выводы: 1. Уравнения Максвелла допускают волновые решения. 2. Электромагнитная
- 12. Экспериментальное открытие электромагнитных волн. 2.
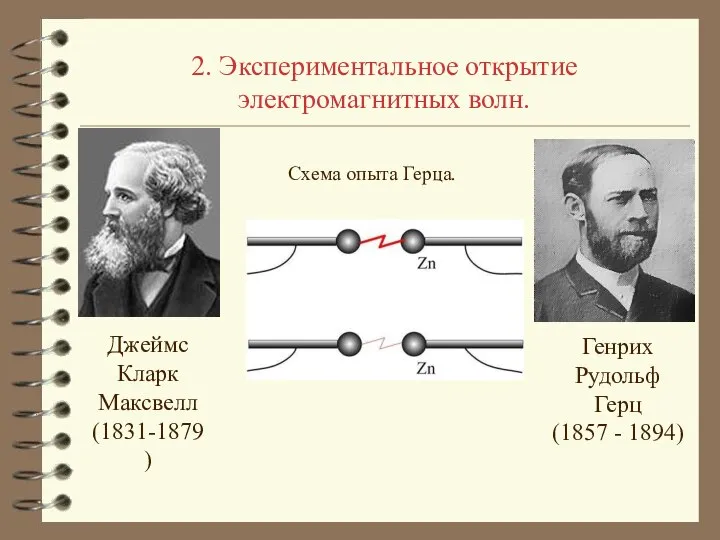
- 13. 2. Экспериментальное открытие электромагнитных волн. Схема опыта Герца. Джеймс Кларк Максвелл (1831-1879)
- 14. Поперечность электромагнитных волн. 3.
- 15. 3. Поперечность ЭМВ. 1. Скорость распространения ЭМВ в вакууме 2. Скорость распространения ЭМВ в любой диэлектрической
- 16. 3. Поперечность ЭМВ. Если плоская ЭМВ распространяется вдоль оси OX выбранной нами системы отсчёта, то её
- 17. 3. Поперечность ЭМВ. ЭМВ распространяется вдоль оси OX, изменение векторов E и H описывается уравнениями Каждая
- 18. 3. Поперечность ЭМВ. Рассмотрим уравнение, описывающее распространение ЭМВ: В левой части этого уравнения То же по
- 19. 3. Поперечность ЭМВ.
- 20. 3. Поперечность ЭМВ. Величина Ex, Ey, Ez зависит только от координаты x, поэтому
- 21. 3. Поперечность ЭМВ. В направлениях, перпендикулярных направлению распространения волны, производные по времен от H нулю не
- 22. 3. Поперечность ЭМВ. Если рассмотреть уравнение, описывающее распространение ЭМВ и, как и в предыдущем случае, переписать
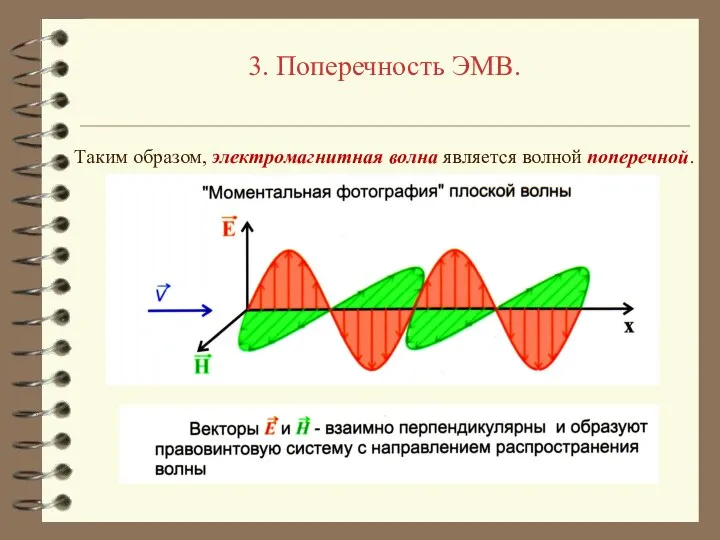
- 23. 3. Поперечность ЭМВ. Таким образом, электромагнитная волна является волной поперечной.
- 24. Поляризация электромагнитных волн. 4.
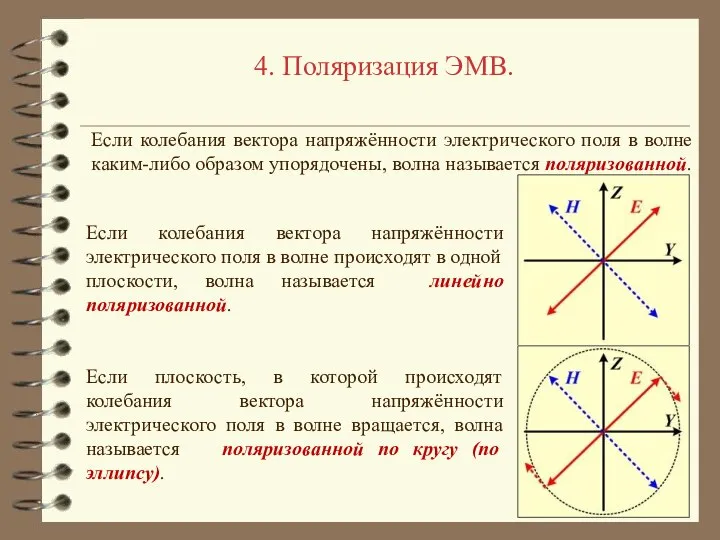
- 25. 4. Поляризация ЭМВ. Если колебания вектора напряжённости электрического поля в волне каким-либо образом упорядочены, волна называется
- 26. Соотношение между величинами E и H в электромагнитной волне. 5.
- 27. 5. Соотношение между E и H в ЭМВ. Рассмотрим уравнение, описывающее распространение ЭМВ: В левой части
- 28. 5. Соотношение между E и H в ЭМВ. Учтём, что вектор E зависит только от координаты
- 29. 5. Соотношение между E и H в ЭМВ. Учтём, что вектор H зависит только от координаты
- 30. 5. Соотношение между E и H в ЭМВ. Как мы установили ранее, Подставим в это уравнение
- 31. 5. Соотношение между E и H в ЭМВ. Волновое число k связано с циклической частотой ω
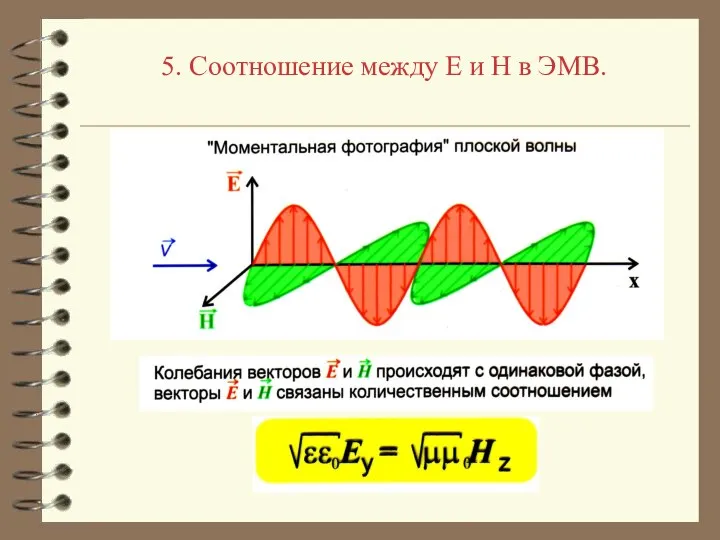
- 32. 5. Соотношение между E и H в ЭМВ.
- 33. Вектор Умова-Пойнтинга. 6.
- 34. 6. Вектор Умова-Пойнтинга. Известно, что плотность энергии электрического поля Эти выражения можно получить из уравнений Максвелла.
- 35. 6. Вектор Умова-Пойнтинга. Если магнитная проницаемость постоянна,
- 36. 6. Вектор Умова-Пойнтинга. Аналогично преобразуем второе уравнение: Мы рассматриваем непроводящую среду, поэтому j = 0. Итого,
- 37. 6. Вектор Умова-Пойнтинга. Из векторного анализа известно тождество: Применив это тождество, получим:
- 38. 6. Вектор Умова-Пойнтинга. Выясним физический смысл полученного выражения. Обозначим Преобразуем левую часть уравнения: - плотность энергии
- 39. 6. Вектор Умова-Пойнтинга. Применим к левой части уравнения теорему Остроградского-Гаусса: Здесь Ω - поверхность, окружающая объём
- 40. 6. Вектор Умова-Пойнтинга. Таким образом, поток вектора Умова-Пойнтинга через некоторую замкнутую поверхность равен убыли энергии электромагнитного
- 41. Энергия, переносимая электромагнитной волной. 7.
- 42. 7. Энергия, переносимая электромагнитной волной. Известно, что плотность энергии электромагнитного поля Если в пространстве распространяется электромагнитная
- 43. 7. Энергия, переносимая электромагнитной волной. Здесь v – скорость электромагнитной волны в данной среде. В вакууме,
- 44. 7. Энергия, переносимая электромагнитной волной. Введём новую величину, S, и назовём её модулем плотности потока энергии.
- 46. Скачать презентацию







































 Только школа способна спасти современную цивилизацию…
Только школа способна спасти современную цивилизацию… авс- свот
авс- свот Мобильные сотовые сети
Мобильные сотовые сети Реформирование местного государственного управления
Реформирование местного государственного управления Пневмонии и гнойные заболевания лёгких. Этиология. Клиника. Диагностика. Осложнения. Основные принципы лечения Доцент Т.Ю.Че
Пневмонии и гнойные заболевания лёгких. Этиология. Клиника. Диагностика. Осложнения. Основные принципы лечения Доцент Т.Ю.Че Классификация природных ресурсов Выполнили студенты 1-ого курса Экономического факультета, Э-122б Иванова Екатерина Родионова А
Классификация природных ресурсов Выполнили студенты 1-ого курса Экономического факультета, Э-122б Иванова Екатерина Родионова А Символ веры
Символ веры Великие художники Холин Е. ПО-21
Великие художники Холин Е. ПО-21 МОУ СОШ № 256 г.Фокино Каратанова Марина Николаевна.
МОУ СОШ № 256 г.Фокино Каратанова Марина Николаевна.  Маркетинг в системе управления предприятиями АПК
Маркетинг в системе управления предприятиями АПК Конвейер. Типы конфликтов
Конвейер. Типы конфликтов Организационно-штатная структура подразделений разведывательного батальона, их состав и предназначение
Организационно-штатная структура подразделений разведывательного батальона, их состав и предназначение Проектирование цифровой системы телевещания
Проектирование цифровой системы телевещания  Модельные характеристики спорта высших достижений. Лекция 2
Модельные характеристики спорта высших достижений. Лекция 2 Презентация Кредитная политика России на современном этапе: оценка ее эффективности
Презентация Кредитная политика России на современном этапе: оценка ее эффективности Построение разрезов
Построение разрезов Інформація та інформаційні процеси Заняття 5 Засоби зберігання та опрацювання інформації
Інформація та інформаційні процеси Заняття 5 Засоби зберігання та опрацювання інформації Исследование роста сосновых насаждений ГКУ КО «Куйбышевское лесничество» и мероприятия по повышению их продуктивности
Исследование роста сосновых насаждений ГКУ КО «Куйбышевское лесничество» и мероприятия по повышению их продуктивности САМОРИМ – Производственная фирма Краткая справка
САМОРИМ – Производственная фирма Краткая справка Droga krzyżowa z Bł. M. Marią Karłowską
Droga krzyżowa z Bł. M. Marią Karłowską Профессиональные навыки и умения политолога
Профессиональные навыки и умения политолога Развитие психических процессов у учащихся на учебном материале по биологии Учитель биологии МОУ СОШ №3 г.Конаково Бубнова Ирина
Развитие психических процессов у учащихся на учебном материале по биологии Учитель биологии МОУ СОШ №3 г.Конаково Бубнова Ирина  Бизнес-план проекта
Бизнес-план проекта Летние Олимпийские игры XVI - ХХ
Летние Олимпийские игры XVI - ХХ Понятие и принципы таможенного права. Выполнили студентки первого курса ФТД группа Т 1205 Жукова Алёна и Зверева Мария.
Понятие и принципы таможенного права. Выполнили студентки первого курса ФТД группа Т 1205 Жукова Алёна и Зверева Мария. Искусство Батика
Искусство Батика Основы теории государства и права Тесты для итогового контроля знаний по всему курсу
Основы теории государства и права Тесты для итогового контроля знаний по всему курсу  Совершенствование системы оплаты труда персонала организации
Совершенствование системы оплаты труда персонала организации