Содержание
- 2. Квадратичная функция Определение График Свойства функции График и свойства функции у = ах2 Сдвиг графика у
- 3. Квадратичная функция Квадратичной функцией называют функцию, которую можно задать формулой вида y = ax2 + bx
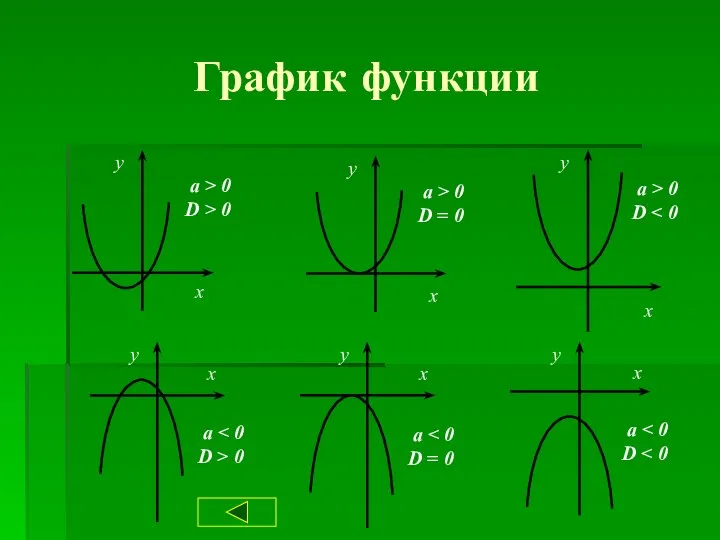
- 4. График функции
- 5. График y = ax2 + bx + c, D = b2 – 4ac - дискриминант M(x0,y0)
- 6. Свойства функции 1. Нули функции: y=0 (пересечения с осью Ох) 2.Точки пересечения с осью Оy 3.Возрастание
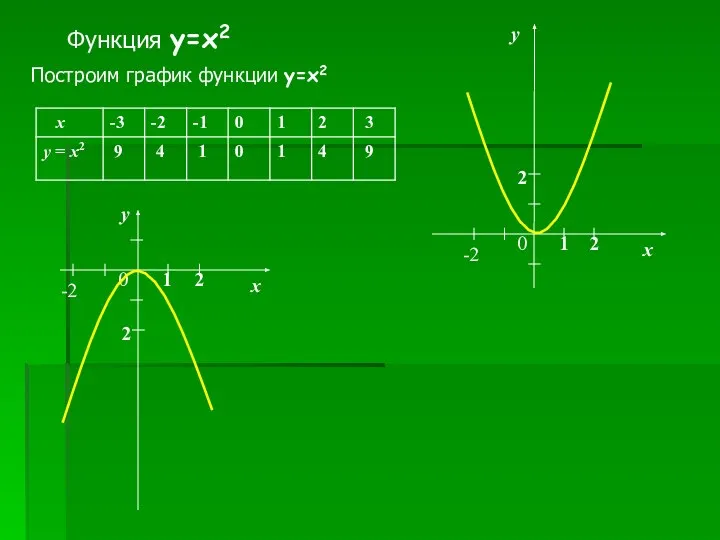
- 7. Функция y=x2 Построим график функции y=x2
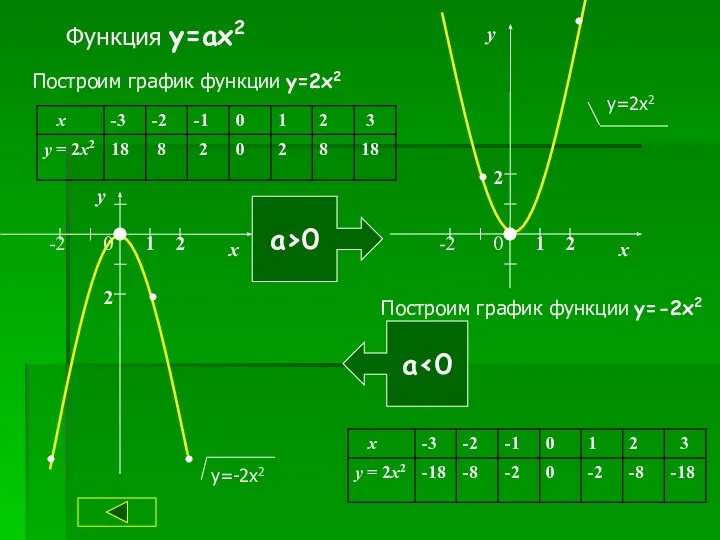
- 8. Функция y=ax2 Построим график функции y=2x2 а>0 а‹0 Построим график функции y=-2x2 у=-2х2 у 0 -2
- 9. График и свойства функции y=ax2 Графиком функции y=ax2, где a≠0, является парабола с вершиной в начале
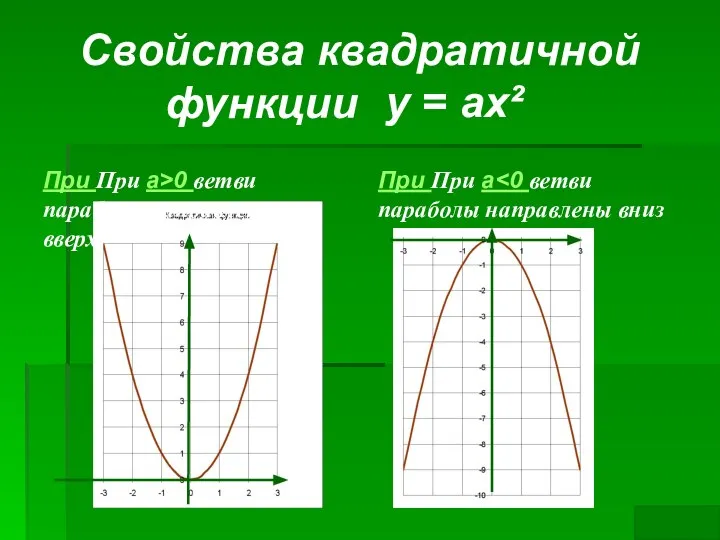
- 10. Свойства квадратичной функции При При a>0 ветви параболы направлены вверх При При a у = ах²
- 11. Свойства у = ах2 при а > 0 y = x2 y = 2x2 y =
- 12. Свойства у = ах2 при а y = - x2 y = - 2x2 y =
- 13. Сдвиг графика функции y = ax2 вдоль осей координат 1. Чтобы построить график функции y =
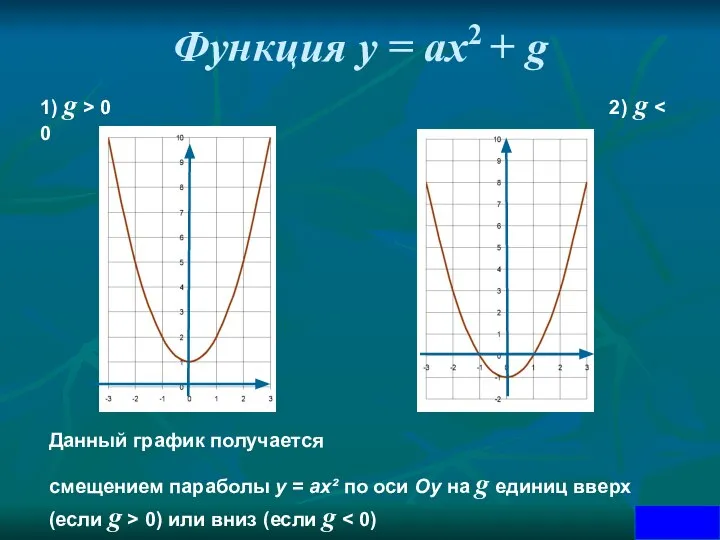
- 14. Функция у = ах2 + g 1) g > 0 2) g Данный график получается смещением
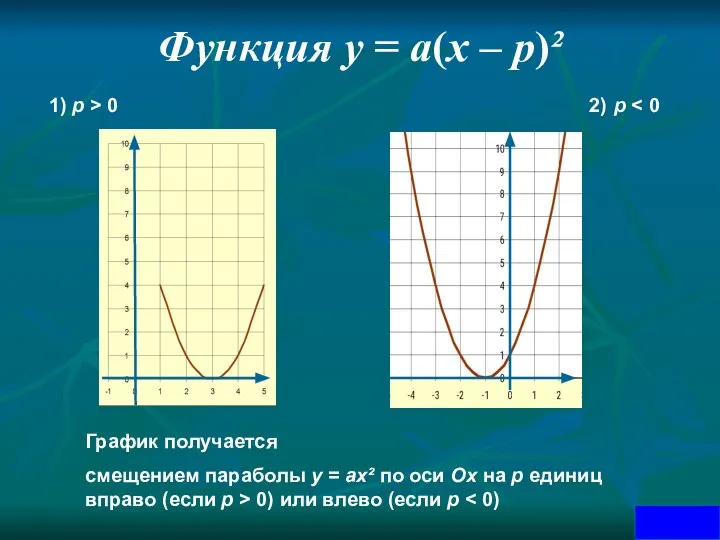
- 15. Функция у = а(х – р)² 1) р > 0 2) р График получается смещением параболы
- 16. Способы построения графика квадратичной функции 1 СПОСОБ 2 СПОСОБ 3 СПОСОБ Пример №1 Пример №2 Пример
- 17. 1 СПОСОБ. Схема построения графика квадратичной функции y=ax2-bx+c: Построить вершину параболы. Провести через вершину параболы прямую,
- 18. 2 СПОСОБ. Построение параболы по точкам с ординатой, равной свободному члену квадратного трёхчлена ax2-bx+c.
- 19. 3 СПОСОБ. y=a(x-m)2 + n График функции y=a(x-m)2+n получается сдвигом графика функции y=ax2 на m единичных
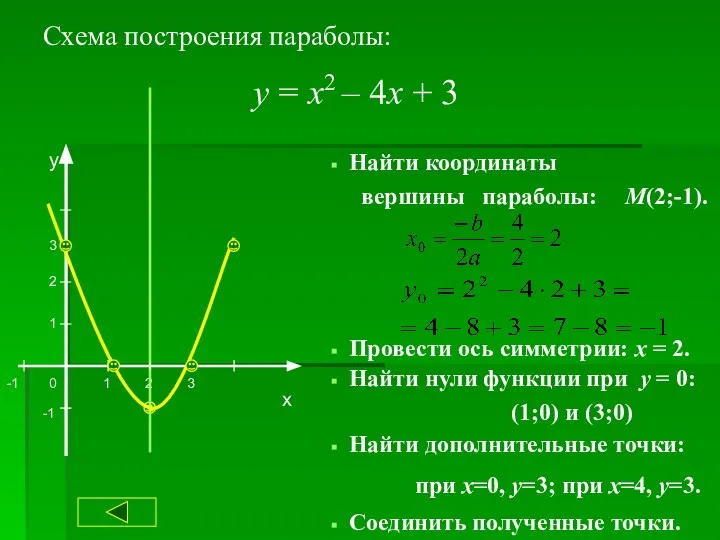
- 20. Схема построения параболы: х у 1 2 -1 -1 1 2 3 0 3 у =
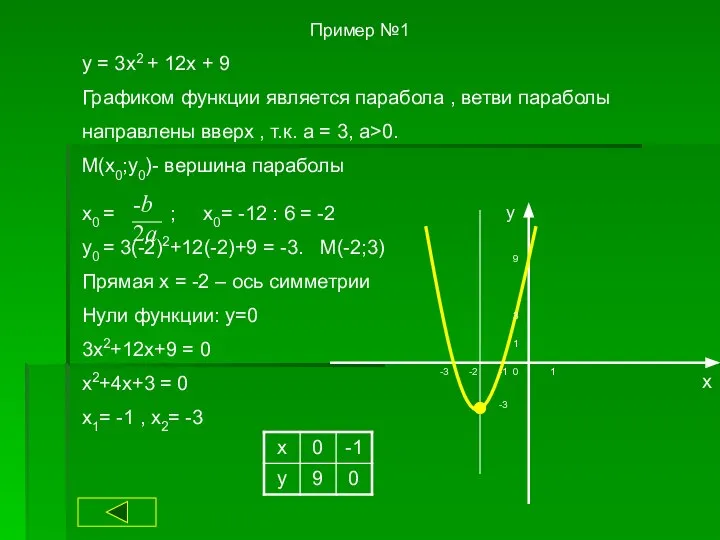
- 21. Пример №1 y = 3x2 + 12x + 9 Графиком функции является парабола , ветви параболы
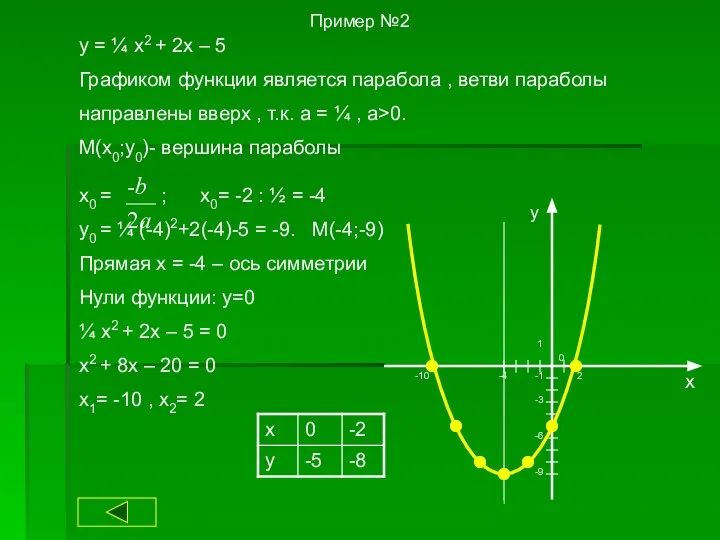
- 22. Пример №2 y = ¼ x2 + 2x – 5 Графиком функции является парабола , ветви
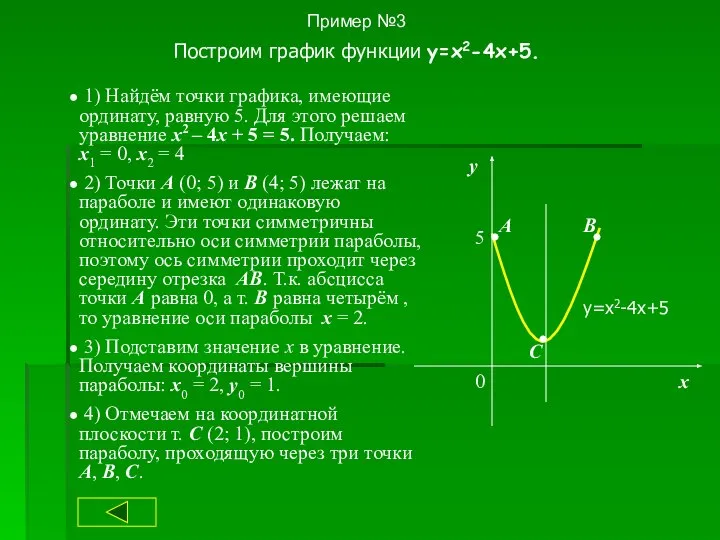
- 23. Пример №3 Построим график функции y=x2-4x+5. 1) Найдём точки графика, имеющие ординату, равную 5. Для этого
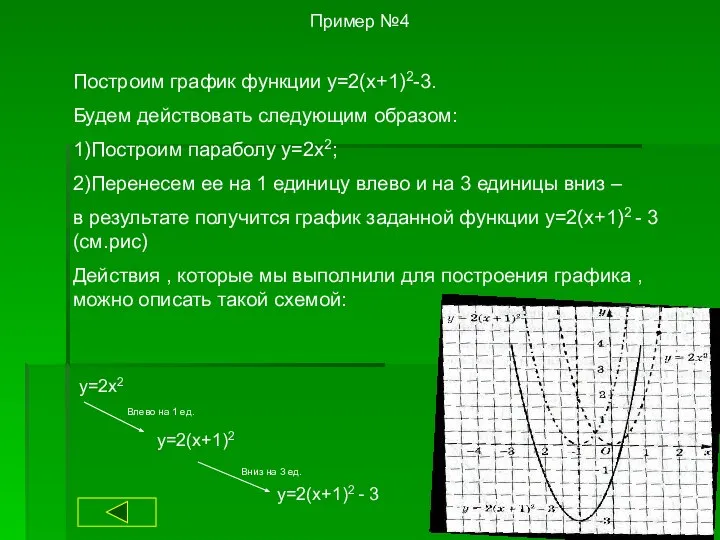
- 24. Пример №4 Построим график функции y=2(x+1)2-3. Будем действовать следующим образом: 1)Построим параболу y=2x2; 2)Перенесем ее на
- 26. Скачать презентацию











 Тема урока АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Тема урока АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ Питание и пища Выполнили: Петрова, Другова Проверила: Трифонова О.Ю
Питание и пища Выполнили: Петрова, Другова Проверила: Трифонова О.Ю Автоматические поточные линии
Автоматические поточные линии ОПЕРАЦИИ ЦЕНТРАЛЬНОГО БАНКА НА ОТКРЫТОМ РЫНКЕ Комаров П. Паркина М. МЭ081
ОПЕРАЦИИ ЦЕНТРАЛЬНОГО БАНКА НА ОТКРЫТОМ РЫНКЕ Комаров П. Паркина М. МЭ081 Разработка модели подсистемы управления освещением
Разработка модели подсистемы управления освещением Сортировка-Пузырёк Выборочная QuickSort
Сортировка-Пузырёк Выборочная QuickSort Презентация "Задачи и организация учета" - скачать презентации по Экономике
Презентация "Задачи и организация учета" - скачать презентации по Экономике Кроссворд по «Истории таможенного дела и таможенной политике» Выполнила студентка 1-ого курса
Кроссворд по «Истории таможенного дела и таможенной политике» Выполнила студентка 1-ого курса  Культура России XVII века
Культура России XVII века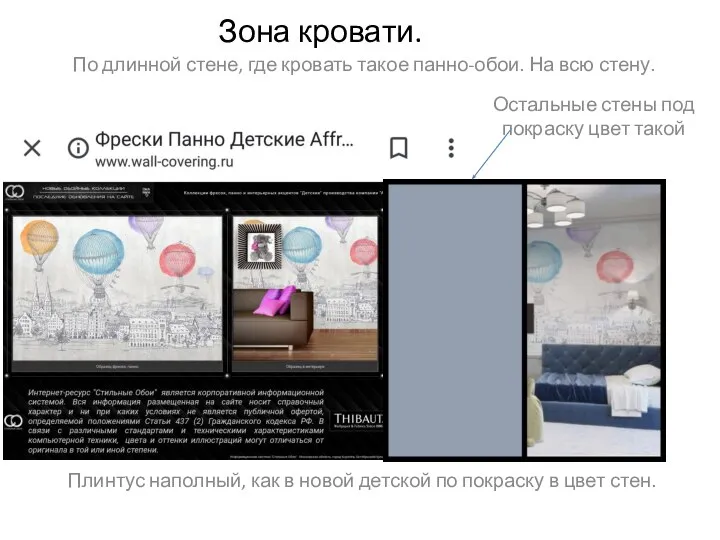 Детская сына
Детская сына Все подвиги Геракл совершил на службе А) у Зевса Б) у Эврисфея В) у Алкмены
Все подвиги Геракл совершил на службе А) у Зевса Б) у Эврисфея В) у Алкмены Государственный контроль и надзор в дизайнерской деятельности
Государственный контроль и надзор в дизайнерской деятельности Вода и здоровье.Методы улучшения качества воды.( 2 курс)
Вода и здоровье.Методы улучшения качества воды.( 2 курс)  Ведение буровзрывных работ на горизонте Южной залежи
Ведение буровзрывных работ на горизонте Южной залежи Модуль «ОСНОВЫ СВЕТСКОЙ ЭТИКИ» УРОК 45. РОД И СЕМЬЯ – ИСТОК НРАВСТВЕННЫХ ОТНОШЕНИЙ В ИСТОРИИ ЧЕЛОВЕЧЕСТВА
Модуль «ОСНОВЫ СВЕТСКОЙ ЭТИКИ» УРОК 45. РОД И СЕМЬЯ – ИСТОК НРАВСТВЕННЫХ ОТНОШЕНИЙ В ИСТОРИИ ЧЕЛОВЕЧЕСТВА Серебряный век русской культуры
Серебряный век русской культуры Идентификация контролируемых товаров и технологий Статья 24. Идентификация контролируемых товаров и технологий  
Идентификация контролируемых товаров и технологий Статья 24. Идентификация контролируемых товаров и технологий   Мультиэлектродные массивы (лекция 4)
Мультиэлектродные массивы (лекция 4) Топологическое проектирование ПП
Топологическое проектирование ПП «ДИФФЕРЕНЦИАЛЬНАЯ ДИАГНОСТИКА АНГИН»
«ДИФФЕРЕНЦИАЛЬНАЯ ДИАГНОСТИКА АНГИН» Транспортная безопасность США
Транспортная безопасность США Преимущества и трудности управления персоналом в холдинговых компаниях «Дао не делает ничего, однако ничего не остается не сдела
Преимущества и трудности управления персоналом в холдинговых компаниях «Дао не делает ничего, однако ничего не остается не сдела Презентация Договор ренты
Презентация Договор ренты Интернет-магазин экологически чистых товаров EcoFutureShop
Интернет-магазин экологически чистых товаров EcoFutureShop Р/р ИЗЛОЖЕНИЕ
Р/р ИЗЛОЖЕНИЕ Культура и религия
Культура и религия ГЕРБЫ И ЭМБЛЕМЫ Изобразительное искусство 5 класс
ГЕРБЫ И ЭМБЛЕМЫ Изобразительное искусство 5 класс Обучение технике ударов по мячу в футболе. _
Обучение технике ударов по мячу в футболе. _