ЛЕКЦИЯ 2. Мысленное математическое моделирование простейшего непрерывного процесса – движения «сосредоточенных
масс»
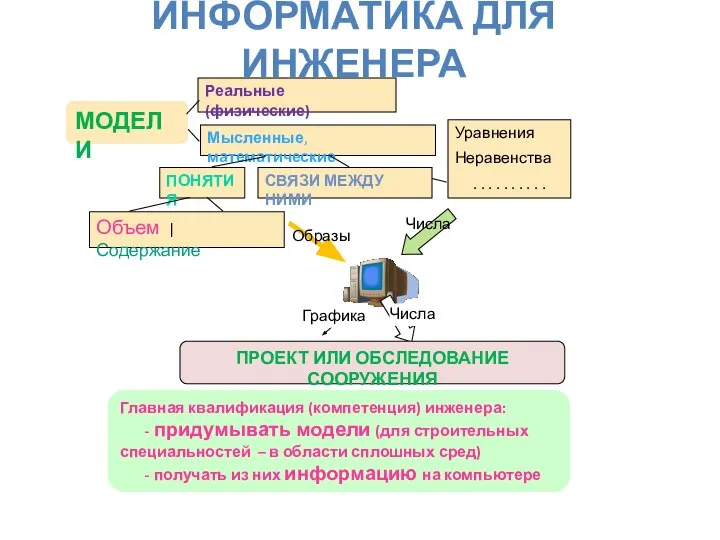
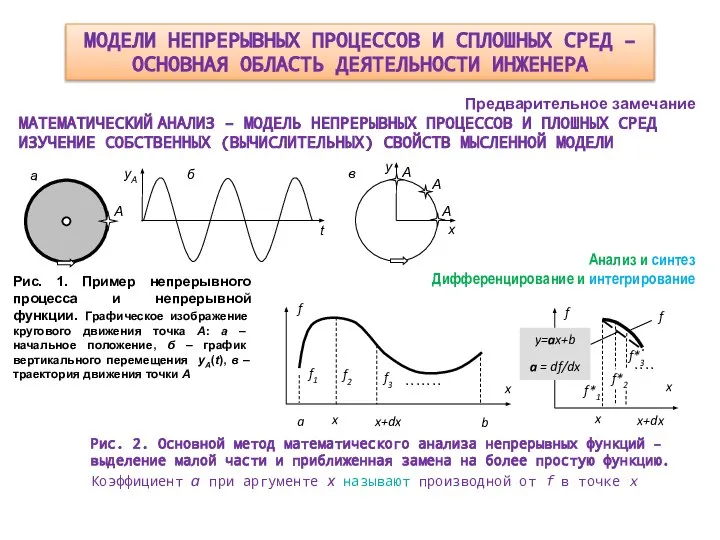
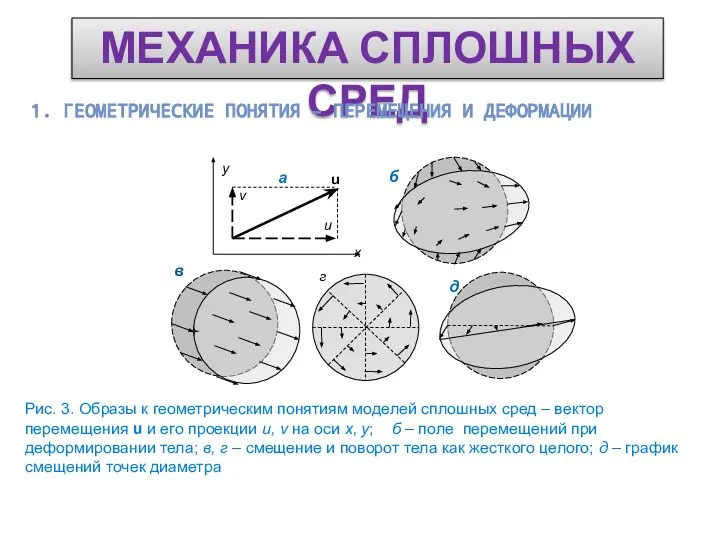
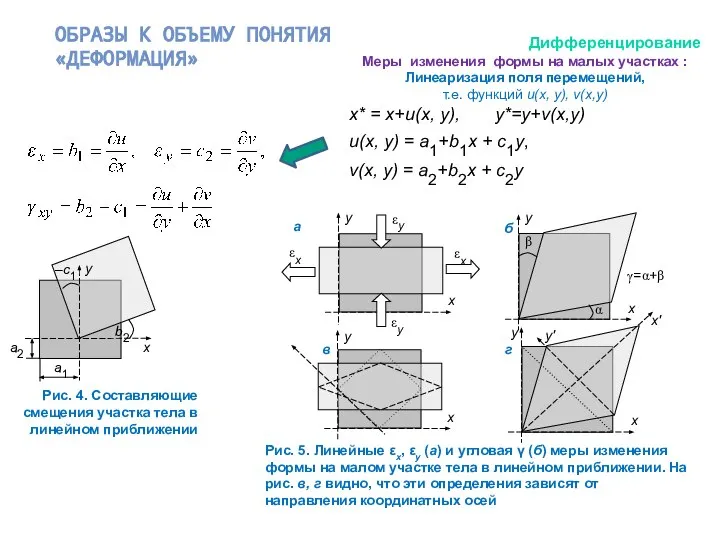
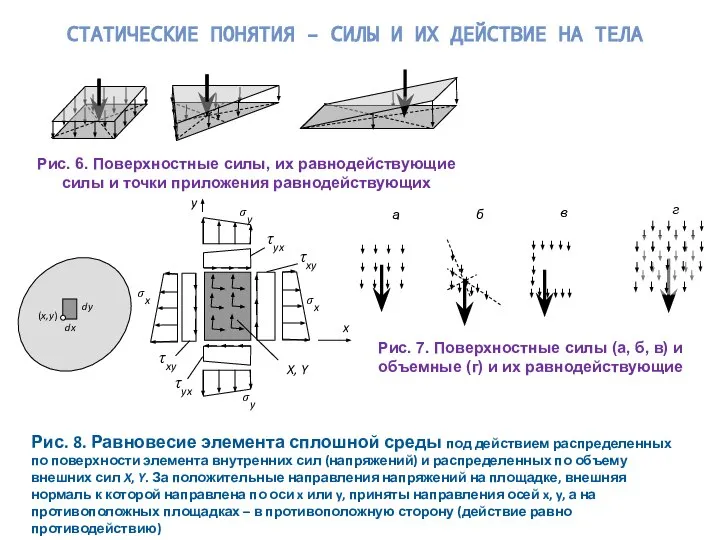
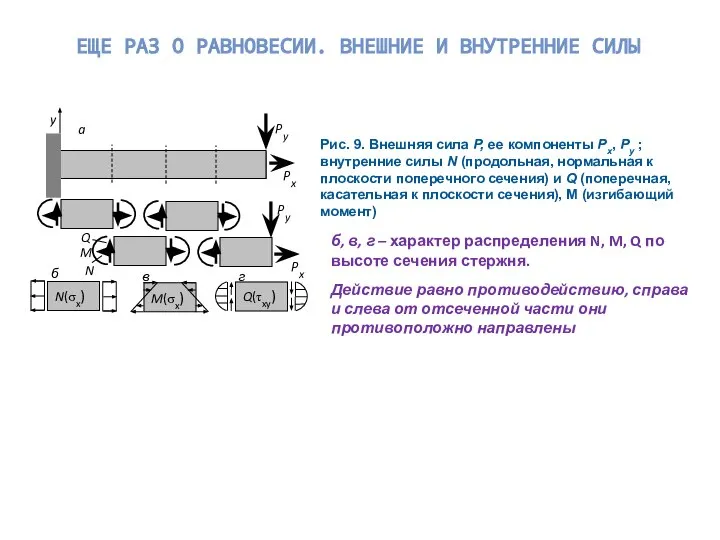
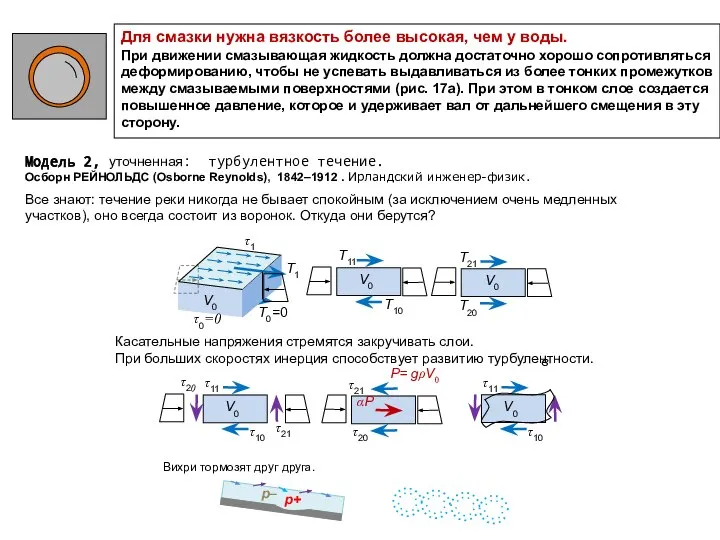
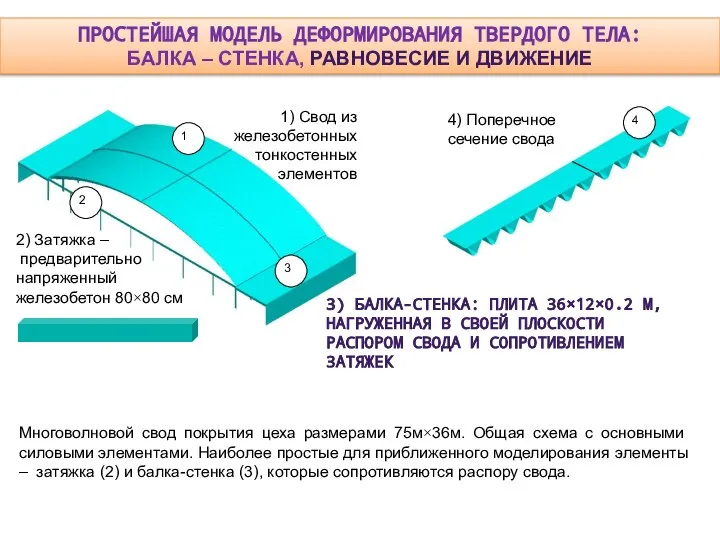
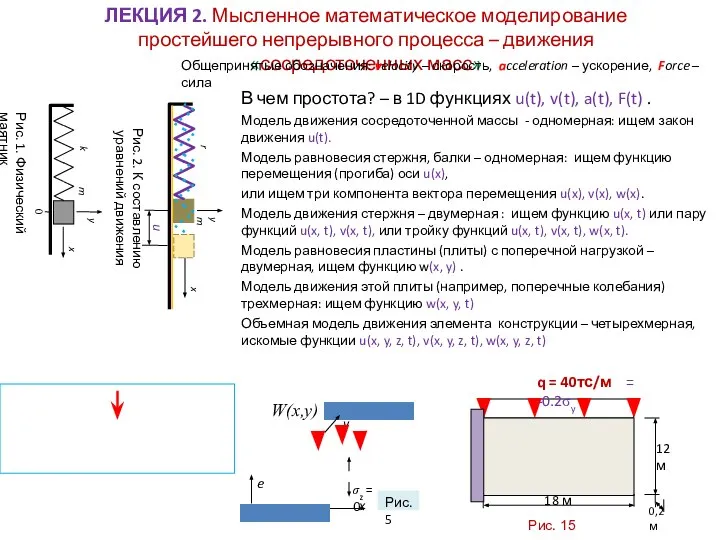
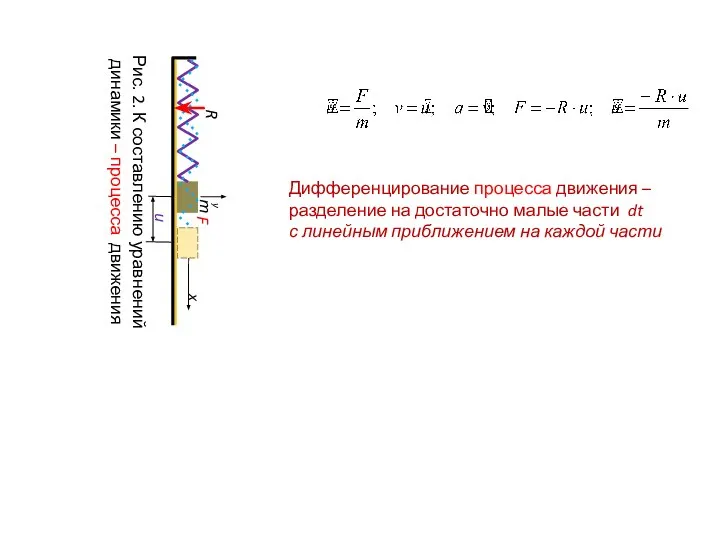
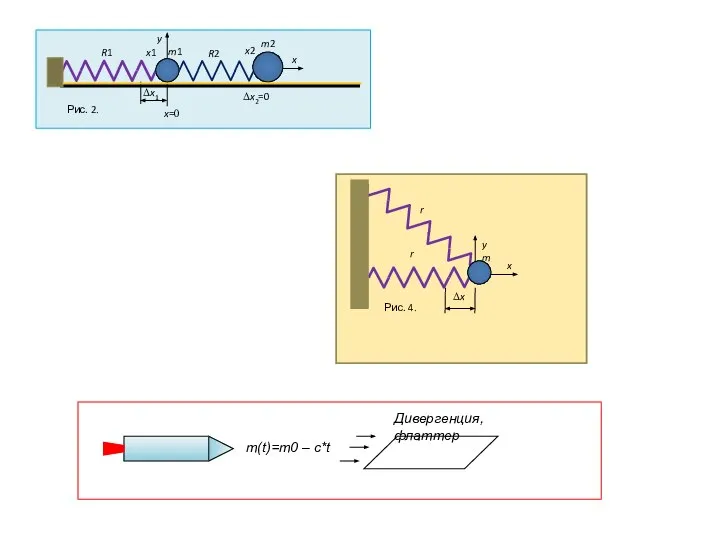
В чем простота? – в 1D функциях u(t), v(t), a(t), F(t) .
Модель движения сосредоточенной массы - одномерная: ищем закон движения u(t).
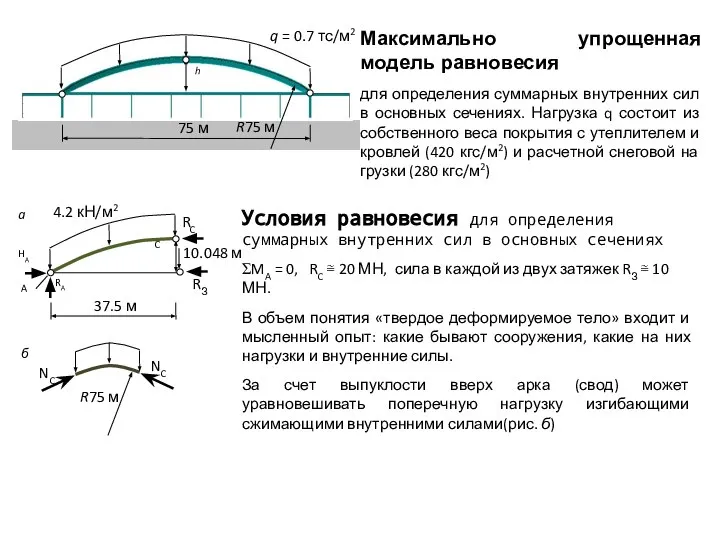
Модель равновесия стержня, балки – одномерная: ищем функцию перемещения (прогиба) оси u(x),
или ищем три компонента вектора перемещения u(x), v(x), w(x).
Модель движения стержня – двумерная : ищем функцию u(x, t) или пару функций u(x, t), v(x, t), или тройку функций u(x, t), v(x, t), w(x, t).
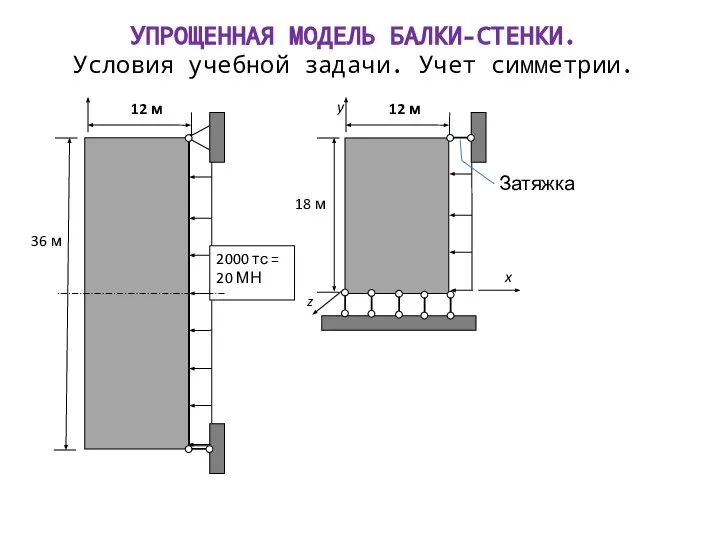
Модель равновесия пластины (плиты) с поперечной нагрузкой – двумерная, ищем функцию w(x, y) .
Модель движения этой плиты (например, поперечные колебания) трехмерная: ищем функцию w(x, y, t)
Объемная модель движения элемента конструкции – четырехмерная, искомые функции u(x, y, z, t), v(x, y, z, t), w(x, y, z, t)
Общепринятые обозначения: velocity – скорость, acceleration – ускорение, Force – сила




 Управление проектами. Лекция 2
Управление проектами. Лекция 2 Концепция стратегического управления Arthur d.little. Модель ADL/LC Дисциплина: Международный маркетинг
Концепция стратегического управления Arthur d.little. Модель ADL/LC Дисциплина: Международный маркетинг  Полное построение алгоритма. Часть 2. Задача коммивояжера
Полное построение алгоритма. Часть 2. Задача коммивояжера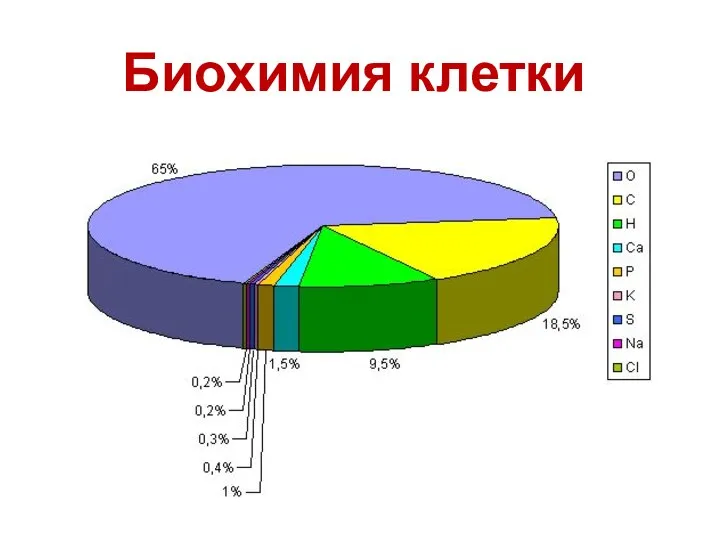 Элементарный состав
Элементарный состав Презентация "Особенности реализации проектов аутсорсинга в российских и зарубежных компаниях" - скачать презентации по Экон
Презентация "Особенности реализации проектов аутсорсинга в российских и зарубежных компаниях" - скачать презентации по Экон Основы радиоэлектроники
Основы радиоэлектроники Деление войск смешариков
Деление войск смешариков Поздравления к 8 Марта
Поздравления к 8 Марта Программа поездки в Казань
Программа поездки в Казань Святитель Николай. Слайдфильм
Святитель Николай. Слайдфильм Программирование на языке MATLAB. Программирование разветвляющих алгоритмов
Программирование на языке MATLAB. Программирование разветвляющих алгоритмов Классицизм (от латинского- «образцовый»)
Классицизм (от латинского- «образцовый») Генеалогическое древо
Генеалогическое древо Спорт, индивидуальный выбор спорта
Спорт, индивидуальный выбор спорта Внутрибольничная инфекция
Внутрибольничная инфекция Стихи Г Виеру - презентация для начальной школы
Стихи Г Виеру - презентация для начальной школы Політичний конфлікт як предмет дослідження геоконфліктології
Політичний конфлікт як предмет дослідження геоконфліктології Разряды прилагательных
Разряды прилагательных Презентация Задача по контрактам
Презентация Задача по контрактам АРХИТЕКТУРА Архитектура г. Омска Приложение к хрестоматии «Музыка, театр, изобразительное искусство Омского Прииртышья»
АРХИТЕКТУРА Архитектура г. Омска Приложение к хрестоматии «Музыка, театр, изобразительное искусство Омского Прииртышья» Контактная задача
Контактная задача Презентация на тему "Профілактика синдрому емоційного вигорання" - скачать презентации по Педагогике
Презентация на тему "Профілактика синдрому емоційного вигорання" - скачать презентации по Педагогике Презентация на тему "Моя профессия - фармацевт" - скачать презентации по Педагогике
Презентация на тему "Моя профессия - фармацевт" - скачать презентации по Педагогике High School Cheerleaders. Комплексная школа черлидеров
High School Cheerleaders. Комплексная школа черлидеров Найти памятники архитектуры XVIII-XIX вв. Найти памятники архитектуры XVIII-XIX вв.
Найти памятники архитектуры XVIII-XIX вв. Найти памятники архитектуры XVIII-XIX вв. Разработка отдельных фаз компиляции для заданного входного языка
Разработка отдельных фаз компиляции для заданного входного языка Презентация на тему "Мышцы" - скачать презентации по Медицине
Презентация на тему "Мышцы" - скачать презентации по Медицине сент
сент