Содержание
- 2. Условия однозначности процесса задаются в виде: – физических параметров – коэффициента теплопроводности, удельной теплоемкости, плотности, формы
- 3. Охлаждение неограниченной пластины Рассмотрим неограниченную пластину (толщина пластины значительно меньше ее длины и ширины) толщиной Примем
- 4. При начальных условиях Поскольку на обеих сторонах пластины отвод теплоты одинаковый, то задача становится симметричной и
- 5. Постоянную выбираем из граничных условий, а знак «-» выбираем из физических соображений, т.к. это очевидно для
- 6. Учитывая граничные условия, имеем: При Или Это возможно только при , т.е. при Таким образом, частное
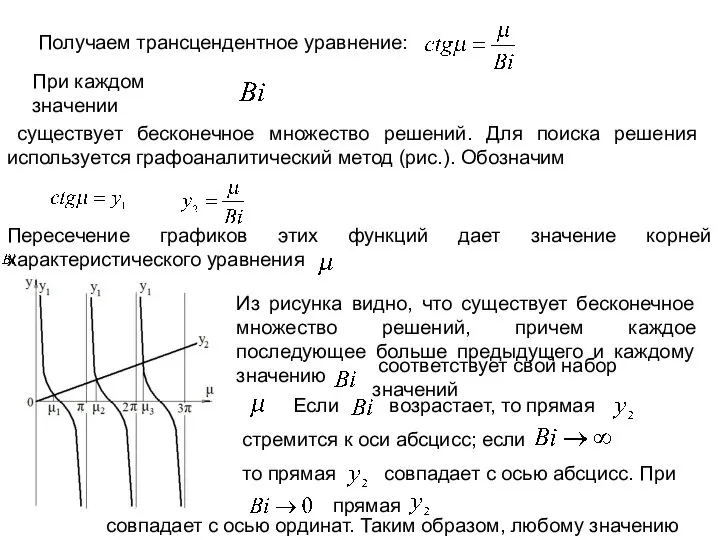
- 7. Получаем трансцендентное уравнение: При каждом значении существует бесконечное множество решений. Для поиска решения используется графоаналитический метод
- 8. будет соответствовать свое распределение температуры: . . . . . . . . . . .
- 9. Откуда определим начальное распределение температуры, учитывая начальные условия Уравнение есть не что иное, как разложение четной
- 10. Тогда выражение для примет вид: После преобразований: Уравнение определяет температурное поле для любого момента времени при
- 11. Отсюда Распределение температуры может быть записано: Переходя к безразмерным координатам (критерий или число Фурье – безразмерное
- 12. тем быстрее убывают члены ряда. При ряд становится быстросходящимся и с достаточной степенью точности распределение температуры
- 13. Зависимость распределения температуры от При малых (рис.б) температура пластины незначительно отличается от температуры на оси, т.е.
- 15. Скачать презентацию











 Ходовые части пассажирских вагонов
Ходовые части пассажирских вагонов Бажанова Анастасия
Бажанова Анастасия Допинг и антидопинговый контроль
Допинг и антидопинговый контроль МІСЦЕ КОНФЛІКТІВ У ЛЮДСЬКОМУ СПІЛКУВАННІ Презентацію зробив: Гарасимів Віктор Вчитель: Осінчук Наталя Василівна
МІСЦЕ КОНФЛІКТІВ У ЛЮДСЬКОМУ СПІЛКУВАННІ Презентацію зробив: Гарасимів Віктор Вчитель: Осінчук Наталя Василівна Культура Японии
Культура Японии Звонкова Мира Михайловна - старейший житель деревни Клещёво
Звонкова Мира Михайловна - старейший житель деревни Клещёво Внешние запоминающиеся устройства
Внешние запоминающиеся устройства Платформа разроботки электронных устройств - Arduino
Платформа разроботки электронных устройств - Arduino Презентация Вычисление производной
Презентация Вычисление производной Современные направления проверки правильности программ (лекция 9 )
Современные направления проверки правильности программ (лекция 9 ) Das osterei ist symbol neues lebens
Das osterei ist symbol neues lebens Тридцатое апреля. Классная работа. Слово о здоровье. Повторяем лексику. Ушанфа Ольга Тимофеевна, учи
Тридцатое апреля. Классная работа. Слово о здоровье. Повторяем лексику. Ушанфа Ольга Тимофеевна, учи Золотое кольцо Руси
Золотое кольцо Руси Дома в древности
Дома в древности Культура детско-родительских отношений в роду
Культура детско-родительских отношений в роду Геополитическое положение и внешняя политика России
Геополитическое положение и внешняя политика России Опоры временных мостов
Опоры временных мостов Политическое лидерство
Политическое лидерство История создания и работы клуба «Азимут»
История создания и работы клуба «Азимут» Physical abilities
Physical abilities Морфология культуры
Морфология культуры Фрикционные передачи
Фрикционные передачи Культура России в XVII веке
Культура России в XVII веке Масленица
Масленица Основные подходы к организации бизнес-планирования в организациях
Основные подходы к организации бизнес-планирования в организациях  Индивидуальный проект по дисциплине "Основы программирования". Отгадай слово у компьютера
Индивидуальный проект по дисциплине "Основы программирования". Отгадай слово у компьютера Одномерные массивы целых чисел. Алгоритмизация и программирование. (9 класс)
Одномерные массивы целых чисел. Алгоритмизация и программирование. (9 класс) Правочки
Правочки