Содержание
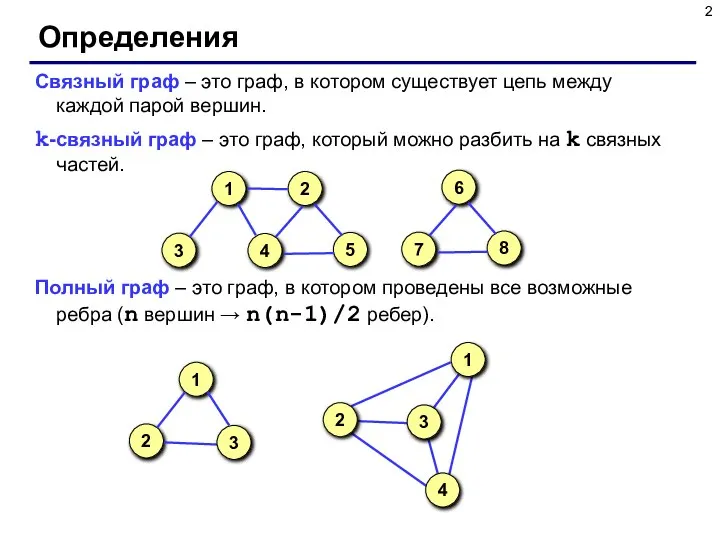
- 2. Определения Связный граф – это граф, в котором существует цепь между каждой парой вершин. k-cвязный граф
- 3. Описание графа Матрица смежности – это матрица, элемент M[i][j] которой равен 1, если существует ребро из
- 4. Весовая матрица Весовая матрица – это матрица, элемент W[i,j] которой равен весу ребра из вершины i
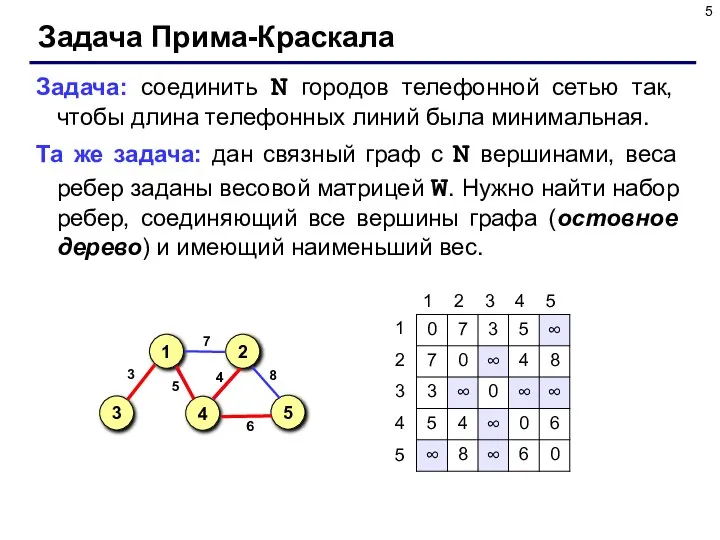
- 5. Задача Прима-Краскала Задача: соединить N городов телефонной сетью так, чтобы длина телефонных линий была минимальная. Та
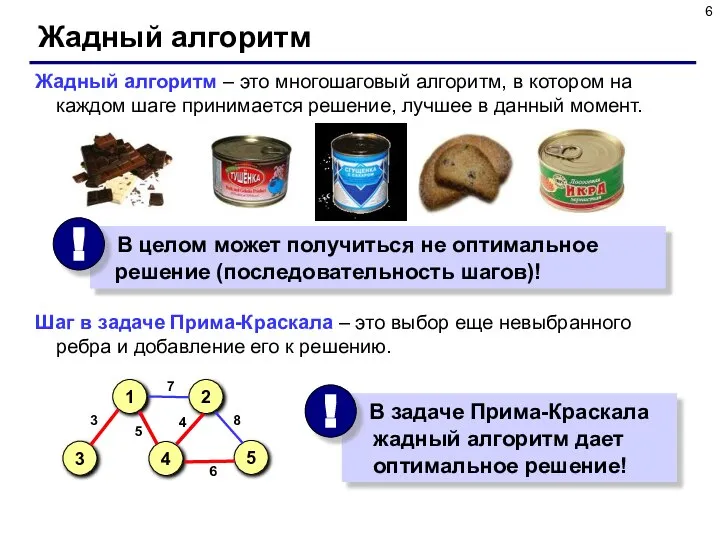
- 6. Жадный алгоритм Жадный алгоритм – это многошаговый алгоритм, в котором на каждом шаге принимается решение, лучшее
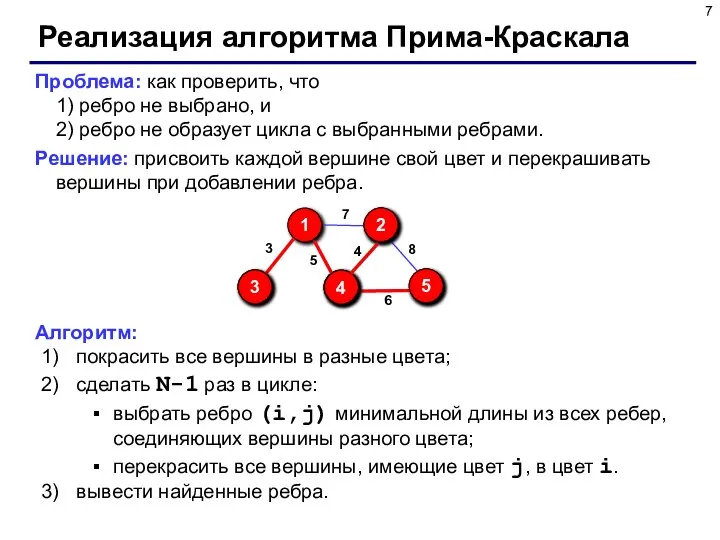
- 7. Реализация алгоритма Прима-Краскала Проблема: как проверить, что 1) ребро не выбрано, и 2) ребро не образует
- 8. Реализация алгоритма Прима-Краскала Структура «ребро»: type rebro = record i, j: integer; { номера вершин }
- 9. Реализация алгоритма Прима-Краскала for k:=1 to N-1 do begin min := MaxInt; for i:=1 to N
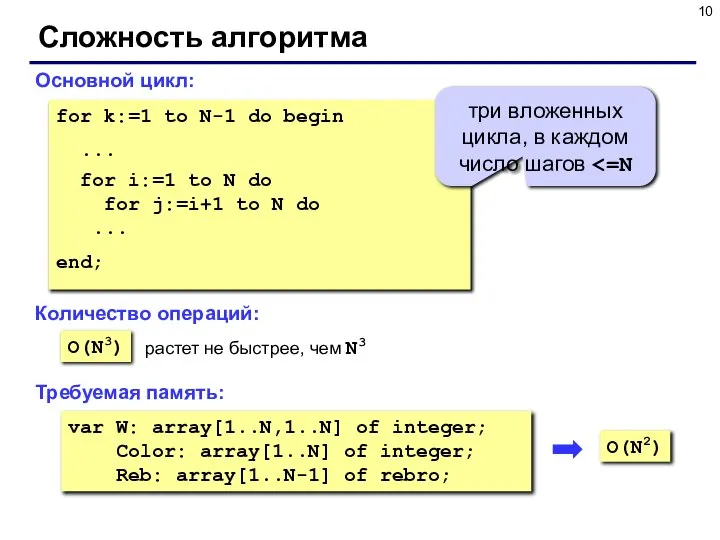
- 10. Сложность алгоритма Основной цикл: O(N3) for k:=1 to N-1 do begin ... for i:=1 to N
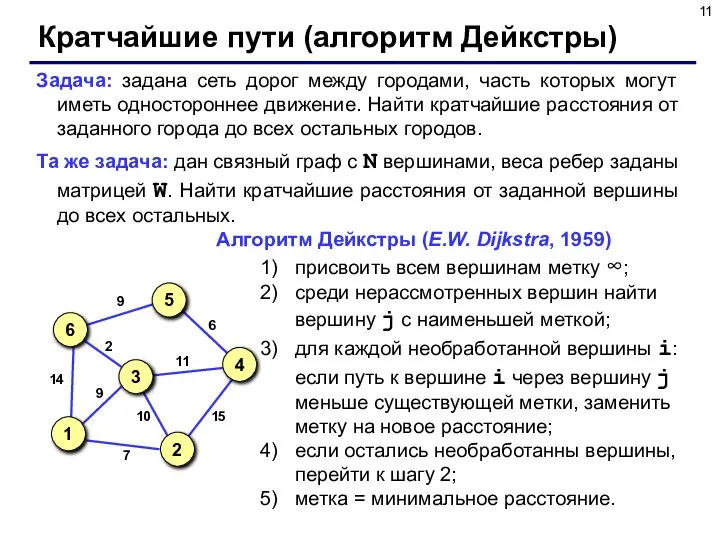
- 11. Кратчайшие пути (алгоритм Дейкстры) Задача: задана сеть дорог между городами, часть которых могут иметь одностороннее движение.
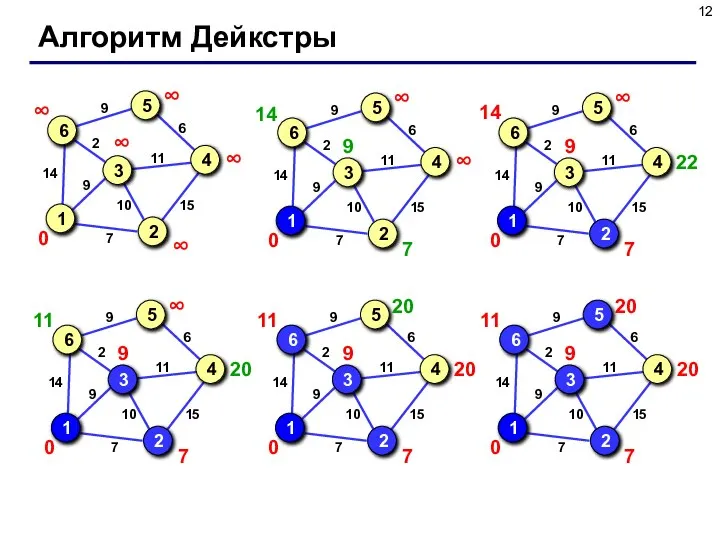
- 12. Алгоритм Дейкстры
- 13. Реализация алгоритма Дейкстры Массивы: массив a, такой что a[i]=1, если вершина уже рассмотрена, и a[i]=0, если
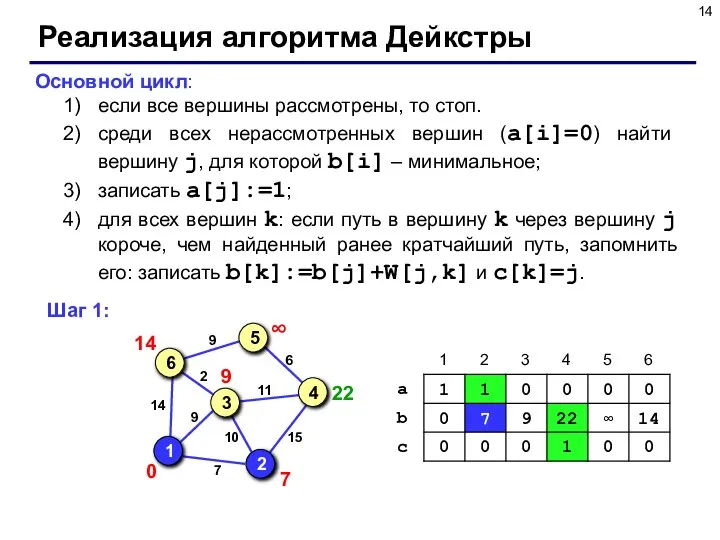
- 14. Реализация алгоритма Дейкстры Основной цикл: если все вершины рассмотрены, то стоп. среди всех нерассмотренных вершин (a[i]=0)
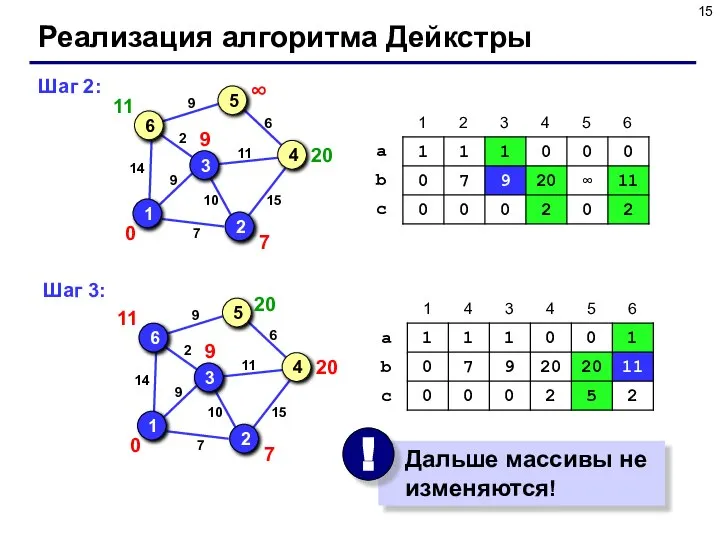
- 15. Реализация алгоритма Дейкстры Шаг 2: Шаг 3:
- 16. Как вывести маршрут? Результат работа алгоритма Дейкстры: длины путей Маршрут из вершины 0 в вершину 4:
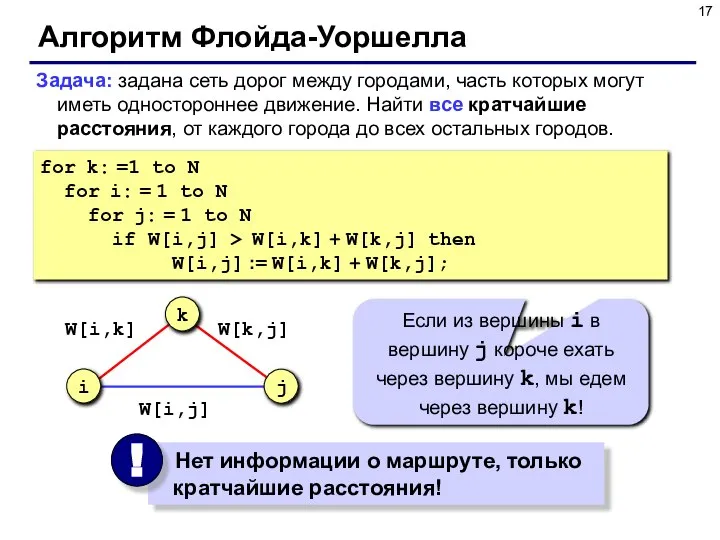
- 17. Алгоритм Флойда-Уоршелла Задача: задана сеть дорог между городами, часть которых могут иметь одностороннее движение. Найти все
- 18. Алгоритм Флойда-Уоршелла Версия с запоминанием маршрута: for i:= 1 to N for j := 1 to
- 19. Задача коммивояжера Задача коммивояжера. Коммивояжер (бродячий торговец) должен выйти из первого города и, посетив по разу
- 21. Скачать презентацию
![Описание графа Матрица смежности – это матрица, элемент M[i][j] которой равен](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1368434/slide-2.jpg)
![Весовая матрица Весовая матрица – это матрица, элемент W[i,j] которой равен](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1368434/slide-3.jpg)


![Реализация алгоритма Дейкстры Массивы: массив a, такой что a[i]=1, если вершина](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1368434/slide-12.jpg)



 Обзор системы. Передача и распределение электроэнергии Copyright © Siemens AG
Обзор системы. Передача и распределение электроэнергии Copyright © Siemens AG мониторы
мониторы Соленое тесто
Соленое тесто Математика в архитектуре Древней Греции и средних веков. Ученик 9 а Рыбалкин Илья Руководитель: Рог
Математика в архитектуре Древней Греции и средних веков. Ученик 9 а Рыбалкин Илья Руководитель: Рог Определение линейной функции - презентация по Алгебре_
Определение линейной функции - презентация по Алгебре_ Первая Медицинская Помощь
Первая Медицинская Помощь  Требования, предъявляемые к управленческим решениям. Лекция 2
Требования, предъявляемые к управленческим решениям. Лекция 2 Упражнения на развитие навыка осознанного чтения Первая группа Логические упражнения
Упражнения на развитие навыка осознанного чтения Первая группа Логические упражнения Религия кельтов
Религия кельтов Профессия психолога Работу выполнила студентка гр.713 факультета иностранных языков ПГПУ Данилова Анастасия
Профессия психолога Работу выполнила студентка гр.713 факультета иностранных языков ПГПУ Данилова Анастасия Симплекс-метод решения задач линейного программирования
Симплекс-метод решения задач линейного программирования ОРГАНИЗАЦИЯ САНИТАРНО-ГИГИЕНИЧЕСКИХ И ПРОТИВОЭПИ-ДЕМИЧЕСКИХ МЕРОПРИЯТИЙ СРЕДИ НАСЕЛЕНИЯ В ВОЕННОЕ ВРЕМЯ
ОРГАНИЗАЦИЯ САНИТАРНО-ГИГИЕНИЧЕСКИХ И ПРОТИВОЭПИ-ДЕМИЧЕСКИХ МЕРОПРИЯТИЙ СРЕДИ НАСЕЛЕНИЯ В ВОЕННОЕ ВРЕМЯ Изображение и обозначение резьбы. Основные параметры резьбы
Изображение и обозначение резьбы. Основные параметры резьбы Буддизм
Буддизм Развитие скоростно-силовых качеств у юношей 16-17 лет на уроках физической культуры
Развитие скоростно-силовых качеств у юношей 16-17 лет на уроках физической культуры Павел Степанович Нахимов
Павел Степанович Нахимов ТОРГОВЛЯ «УНИВЕРСАМЫ,СУПЕРМАРКЕТЫ» 5 класс ГБС(К)ОУ школа –интернат VIIIвида станицы Медведовской Учитель социально-бытовой ор
ТОРГОВЛЯ «УНИВЕРСАМЫ,СУПЕРМАРКЕТЫ» 5 класс ГБС(К)ОУ школа –интернат VIIIвида станицы Медведовской Учитель социально-бытовой ор Подсудность и подготовка судебного заседания
Подсудность и подготовка судебного заседания Родителям о наркотиках «Гаси искру до пожара, беду отводи до удара» (народная пословица)
Родителям о наркотиках «Гаси искру до пожара, беду отводи до удара» (народная пословица) Образ матери в скульптуре 10 класс 2011 – 2012 уч.год
Образ матери в скульптуре 10 класс 2011 – 2012 уч.год оригами кувшинка - презентация для начальной школы
оригами кувшинка - презентация для начальной школы Совершенствование правового статуса государственных учреждений
Совершенствование правового статуса государственных учреждений La cocina española
La cocina española ТЕНГЕ
ТЕНГЕ ФОРМЫ И МЕТОДЫ РАБОТЫ С РОДИТЕЛЯМИ Формы и методы работы с родителями должны быть направлены на повышение педагогической культур
ФОРМЫ И МЕТОДЫ РАБОТЫ С РОДИТЕЛЯМИ Формы и методы работы с родителями должны быть направлены на повышение педагогической культур Презентация машин went-car
Презентация машин went-car Детали мехатронных модулей, роботов и их конструирование направляющие
Детали мехатронных модулей, роботов и их конструирование направляющие Запомнить твёрдо нужно нам – пожар не возникает сам! Владимир Маяковский
Запомнить твёрдо нужно нам – пожар не возникает сам! Владимир Маяковский