Содержание
- 2. Содержание 6. Определение ускорения точки плоской фигуры 1. Уравнения и характеристики плоскопараллельного движения тела 2. Определение
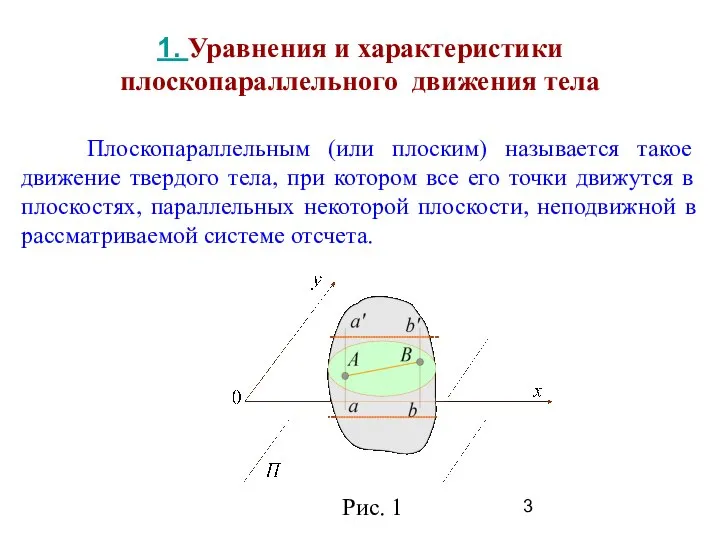
- 3. 1. Уравнения и характеристики плоскопараллельного движения тела Плоскопараллельным (или плоским) называется такое движение твердого тела, при
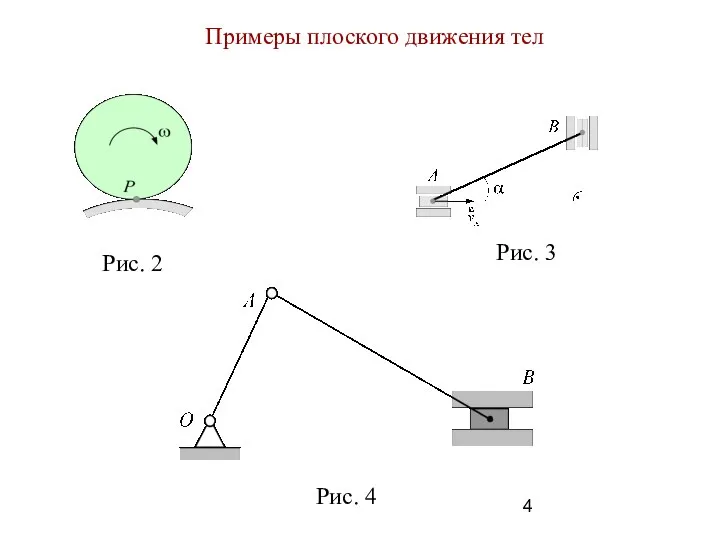
- 4. Примеры плоского движения тел
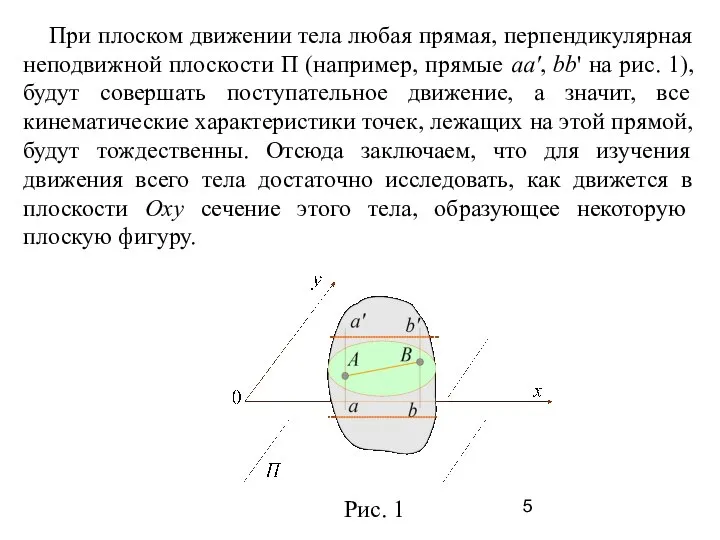
- 5. При плоском движении тела любая прямая, перпендикулярная неподвижной плоскости П (например, прямые аа', bb' на рис.
- 6. Положение плоской фигуры в плоскости Оху определяется положением какого-либо проведенного на этой фигуре отрезка АВ (рис.
- 7. Таким образом, движение плоской фигуры в её плоскости, а следовательно, и плоскопараллельного движения твердого тела относительно
- 8. можно заключить, что движение плоской фигуры в ее плоскости представляет собой совокупность двух движений: поступатель-ного движения,
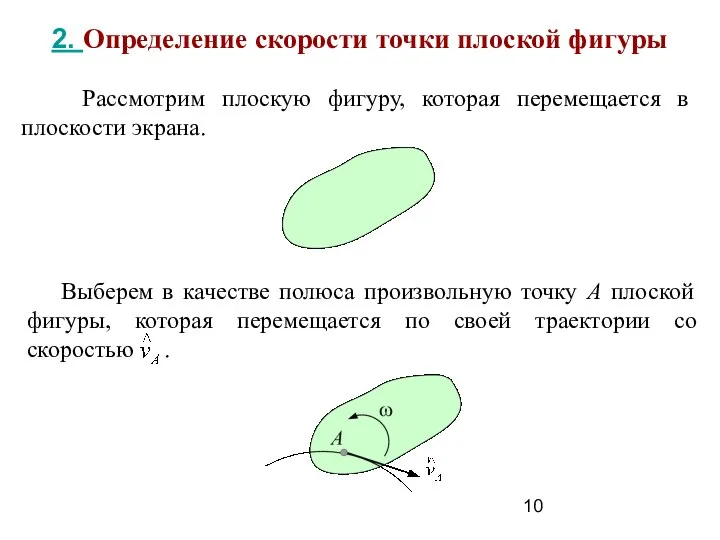
- 10. 2. Определение скорости точки плоской фигуры Рассмотрим плоскую фигуру, которая перемещается в плоскости экрана.
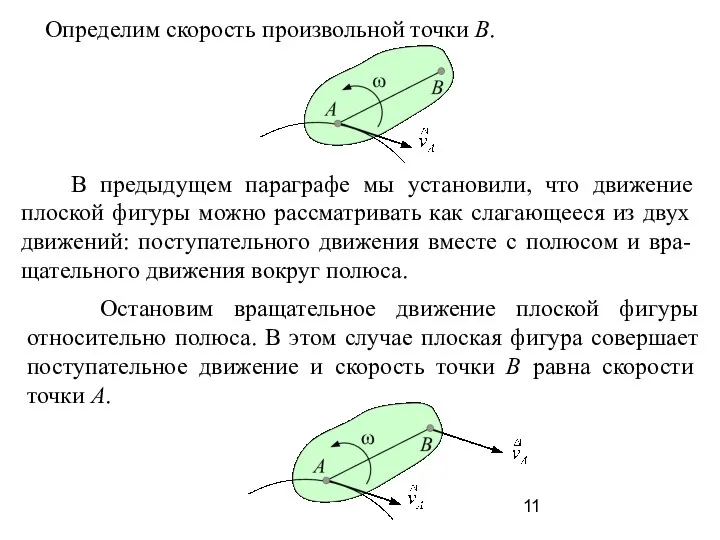
- 11. В предыдущем параграфе мы установили, что движение плоской фигуры можно рассматривать как слагающееся из двух движений:
- 12. Остановим поступательное движение плоской фигуры. Точка В во вращательном движении вокруг полюс А будет иметь скорость,
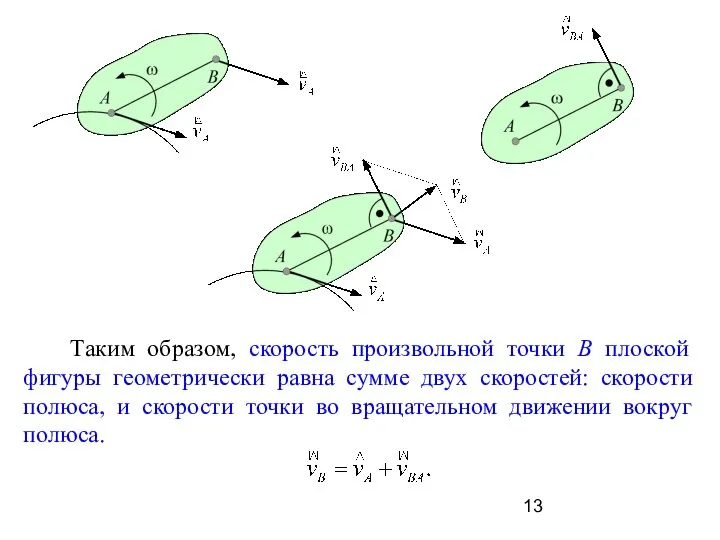
- 13. Таким образом, скорость произвольной точки В плоской фигуры геометрически равна сумме двух скоростей: скорости полюса, и
- 14. Приведенное векторное равенство получило название формулы Эйлера. В соответствии с правилами векторной алгебры модуль скорости точки
- 15. 3. Теорема о проекциях скоростей двух точек плоской фигуры Для двух произвольных точек плоской фигуры А
- 16. Проведём через точки АВ ось x и спроецируем на неё векторное выражение формулы Эйлера:
- 17. Таким образом мы доказали теорему: проекции скоростей двух произвольных точек плоской фигуры на ось, проведённую через
- 18. 4. Мгновенный центр скоростей Из точки А построим перпендикуляр к вектору скорости точки и отложим на
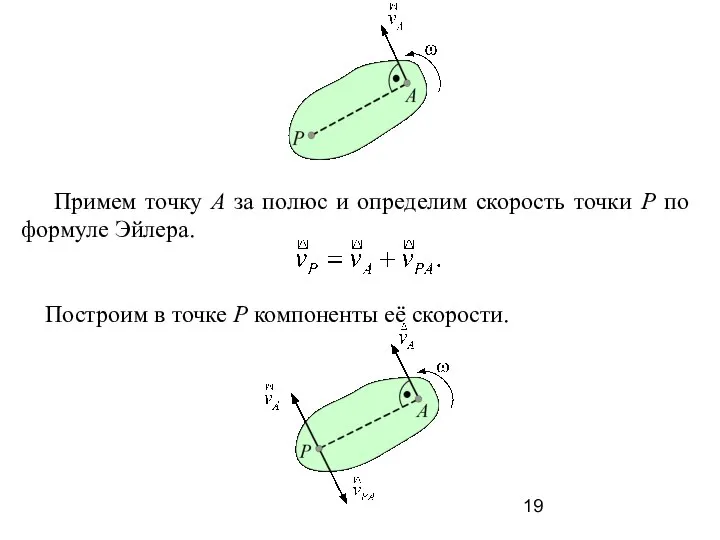
- 19. Примем точку А за полюс и определим скорость точки Р по формуле Эйлера. Построим в точке
- 20. Как видим, эти векторы имеют противоположное направ-ление. Точка плоской фигуры, скорость которой в данный момент времени
- 21. Мгновенный центр скоростей находится на перпендикуляре к вектору скорости любой точки плоской фигуры и может быть
- 22. 5. Определение положения мгновенного центра скоростей Скорости точек равны:
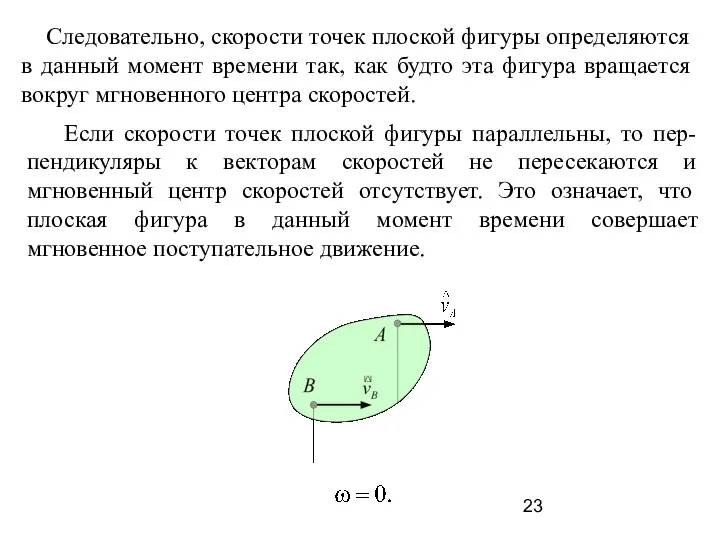
- 23. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как будто эта фигура вращается
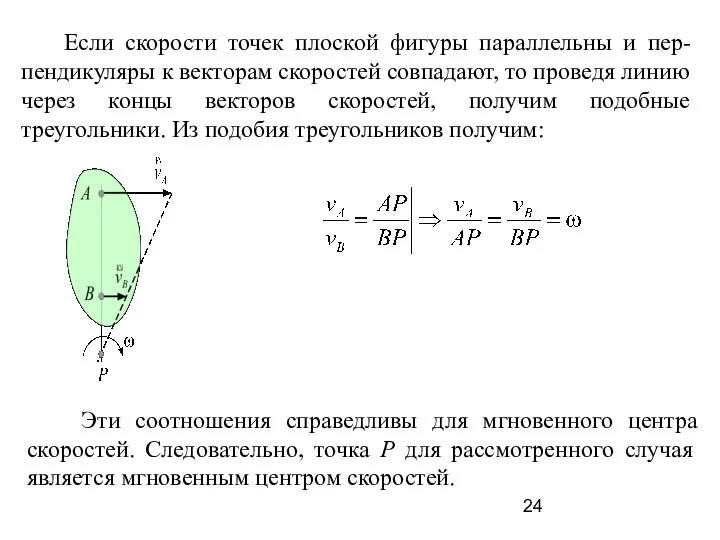
- 24. Если скорости точек плоской фигуры параллельны и пер-пендикуляры к векторам скоростей совпадают, то проведя линию через
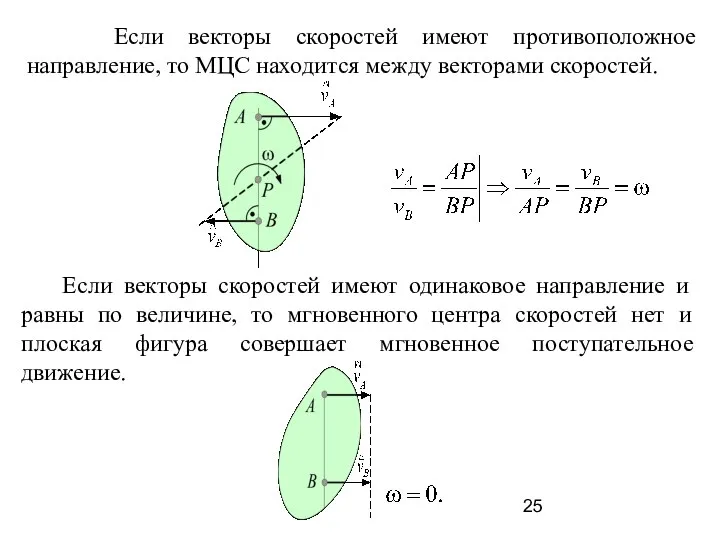
- 25. Если векторы скоростей имеют противоположное направление, то МЦС находится между векторами скоростей. Если векторы скоростей имеют
- 26. 6. Определение ускорения точки плоской фигуры Рассмотрим плоскую фигуру. Примем точку А за полюс и определим
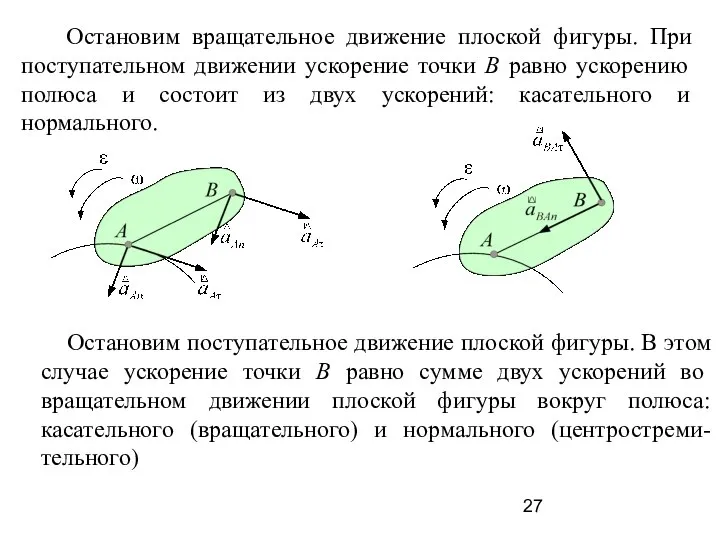
- 27. Остановим вращательное движение плоской фигуры. При поступательном движении ускорение точки В равно ускорению полюса и состоит
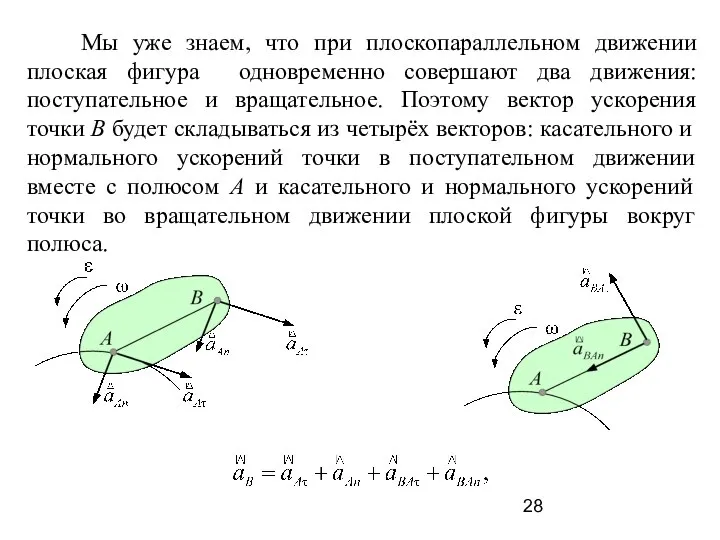
- 28. Мы уже знаем, что при плоскопараллельном движении плоская фигура одновременно совершают два движения: поступательное и вращательное.
- 29. Складывая векторы ускорений точки В в поступательном и вращательном движениях плоской фигуры, получим: Таким образом, ускорение
- 30. На практике при решении задач ускорение точки плоской фигуры раскладывают на компоненты а затем это векторное
- 32. Скачать презентацию

















 аппарат движения
аппарат движения Когда и чем нанолекарства лучше традиционных
Когда и чем нанолекарства лучше традиционных ЛЕКЦИЯ №4 ДЫХАТЕЛЬНАЯ ГИМНАСТИКА ДЛЯ БЕРЕМЕННЫХ Др. Нагаева С.Я.
ЛЕКЦИЯ №4 ДЫХАТЕЛЬНАЯ ГИМНАСТИКА ДЛЯ БЕРЕМЕННЫХ Др. Нагаева С.Я.  Аудиторская выборка и другие процедуры выборочной проверки
Аудиторская выборка и другие процедуры выборочной проверки Республика Ирак
Республика Ирак Презентация «РОЗНИЧНАЯ КУПЛЯ-ПРОДАЖА»
Презентация «РОЗНИЧНАЯ КУПЛЯ-ПРОДАЖА» КОМПЬЮТЕРНАЯ ГРАФИКА 08.11.14
КОМПЬЮТЕРНАЯ ГРАФИКА 08.11.14 Регулирование частоты вращения электроприводов постоянного и переменного тока
Регулирование частоты вращения электроприводов постоянного и переменного тока Poryadok_vypolneniya_zadaniya_KR
Poryadok_vypolneniya_zadaniya_KR Методы сортировки данных
Методы сортировки данных Нарушения белкового обмена
Нарушения белкового обмена Веб-сторінки. ВеБ-сайти. Етапи створення веб-сайтів
Веб-сторінки. ВеБ-сайти. Етапи створення веб-сайтів Дисциплина профессионального цикла для студентов, обучающихся по магистерским программам
Дисциплина профессионального цикла для студентов, обучающихся по магистерским программам  спрос и предложение
спрос и предложение  Перегрузка методов. Объектно - ориентированное программирование
Перегрузка методов. Объектно - ориентированное программирование Самое дорогое - презентация для начальной школы
Самое дорогое - презентация для начальной школы Глава 1 Принципы экономики 3. Рыночная система экономики
Глава 1 Принципы экономики 3. Рыночная система экономики  ОБМЕН ФОСФОЛИПИДОВ И СТЕРОИДОВ
ОБМЕН ФОСФОЛИПИДОВ И СТЕРОИДОВ Разработка через тестирование
Разработка через тестирование Финансовая среда предпринимательства и предпринимательские риски
Финансовая среда предпринимательства и предпринимательские риски Годы жизни М.Ю. Лермонтова (1814 – 1841)
Годы жизни М.Ю. Лермонтова (1814 – 1841) Управление процессами. Взаимодействие процессов: синхронизация, тупики
Управление процессами. Взаимодействие процессов: синхронизация, тупики Тематический план учебной дисциплины «Автоматизированные системы управления и связь»
Тематический план учебной дисциплины «Автоматизированные системы управления и связь» Хлеб - всему голова Выполнил: обучающийся 4 а класса Касьянов Максим МОУ СОШ № 8
Хлеб - всему голова Выполнил: обучающийся 4 а класса Касьянов Максим МОУ СОШ № 8 Презентация Основные направления налогово-бюджетной политики России в современных условиях
Презентация Основные направления налогово-бюджетной политики России в современных условиях  The London Parliament building is known in history as the Palace of Westminster
The London Parliament building is known in history as the Palace of Westminster Презентация "Смоленск – древнейший город России" - скачать презентации по МХК
Презентация "Смоленск – древнейший город России" - скачать презентации по МХК СКУД_БИОМЕТРИЯ_2.ppt
СКУД_БИОМЕТРИЯ_2.ppt