Содержание
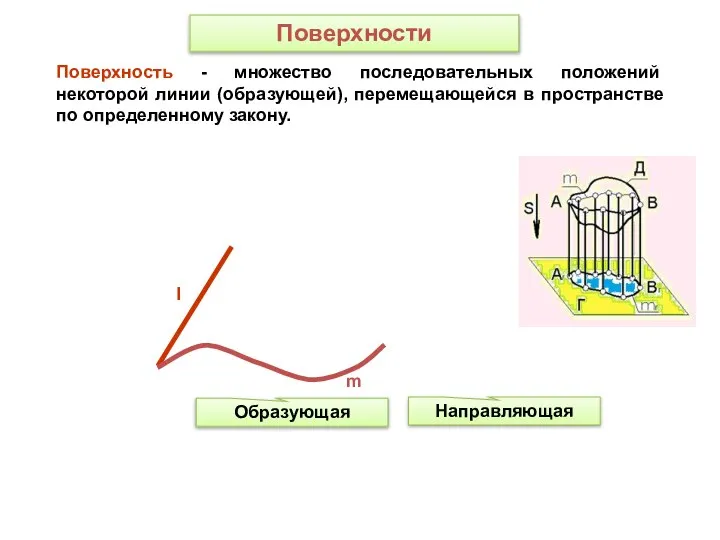
- 2. l Образующая Направляющая m Поверхность - множество последовательных положений некоторой линии (образующей), перемещающейся в пространстве по
- 3. Линия, которая при перемещении образует поверхность, называется образующей. Линии, которые остаются неподвижными и с которыми при
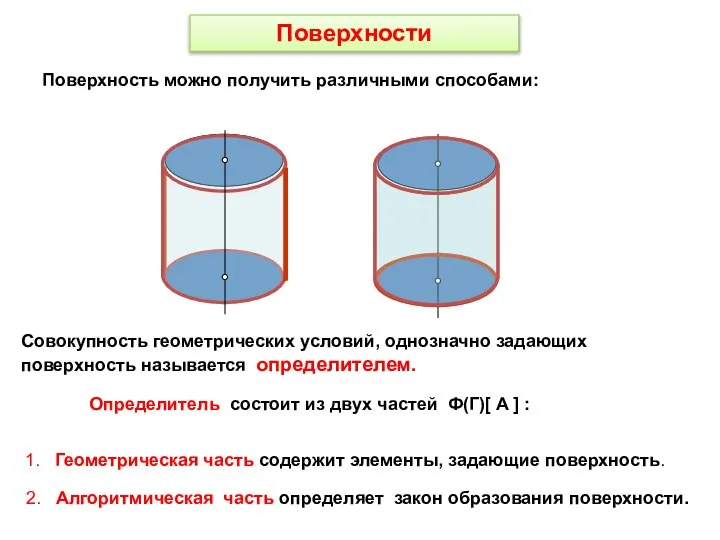
- 4. Поверхности Поверхность можно получить различными способами: Совокупность геометрических условий, однозначно задающих поверхность называется определителем. Определитель состоит
- 5. Классификация поверхностей
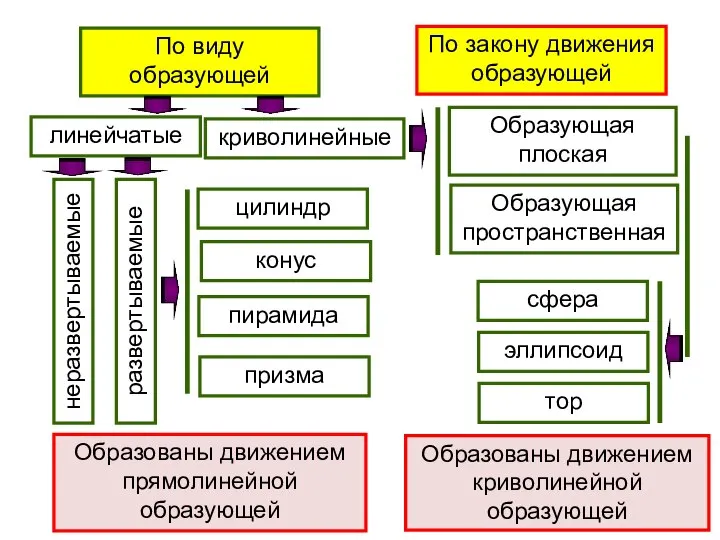
- 6. По виду образующей По закону движения образующей линейчатые криволинейные развертываемые неразвертываемые цилиндр конус пирамида призма Образующая
- 7. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ По виду образующей различают поверхности линейчатые и нелинейчатые. Линейчатые поверхности - поверхности, которые могут
- 8. ЗНАЧИТЕЛЬНЫЙ КЛАСС ПОВЕРХНОСТЕЙ ФОРМИРУЕТСЯ ДВИЖЕНИЕМ ОКРУЖНОСТИ ПОСТОЯННОГО ИЛИ ПЕРЕМЕННОГО РАДИУСА. ЭТО ТАК НАЗЫВАЕМЫЕ ЦИКЛИЧЕСКИЕ ПОВЕРХНОСТИ Циклическая
- 9. ЕСЛИ ЖЕ ГРУППИРОВАТЬ ПОВЕРХНОСТИ ПО ЗАКОНУ ДВИЖЕНИЯ ОБРАЗУЮЩЕЙ ЛИНИИ И ПРОИЗВОДЯЩЕЙ ПОВЕРХНОСТИ, ТО БОЛЬШИНСТВО ВСТРЕЧАЮЩИХСЯ В
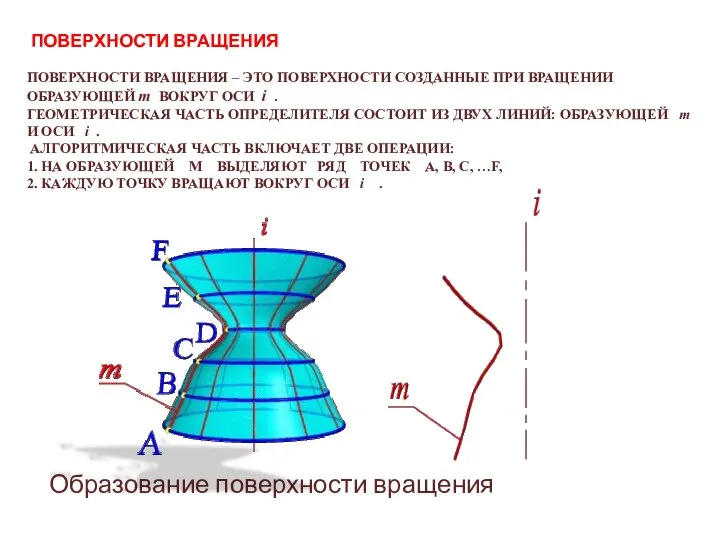
- 10. ПОВЕРХНОСТИ ВРАЩЕНИЯ ПОВЕРХНОСТИ ВРАЩЕНИЯ – ЭТО ПОВЕРХНОСТИ СОЗДАННЫЕ ПРИ ВРАЩЕНИИ ОБРАЗУЮЩЕЙ m ВОКРУГ ОСИ i .
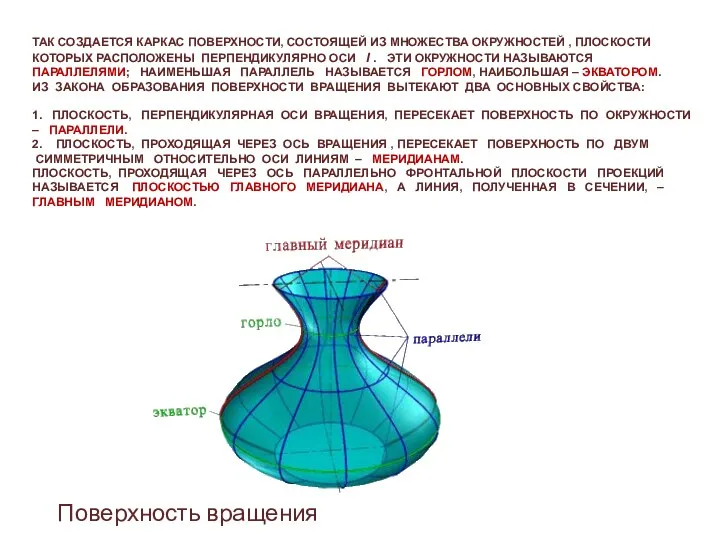
- 11. ТАК СОЗДАЕТСЯ КАРКАС ПОВЕРХНОСТИ, СОСТОЯЩЕЙ ИЗ МНОЖЕСТВА ОКРУЖНОСТЕЙ , ПЛОСКОСТИ КОТОРЫХ РАСПОЛОЖЕНЫ ПЕРПЕНДИКУЛЯРНО ОСИ I .
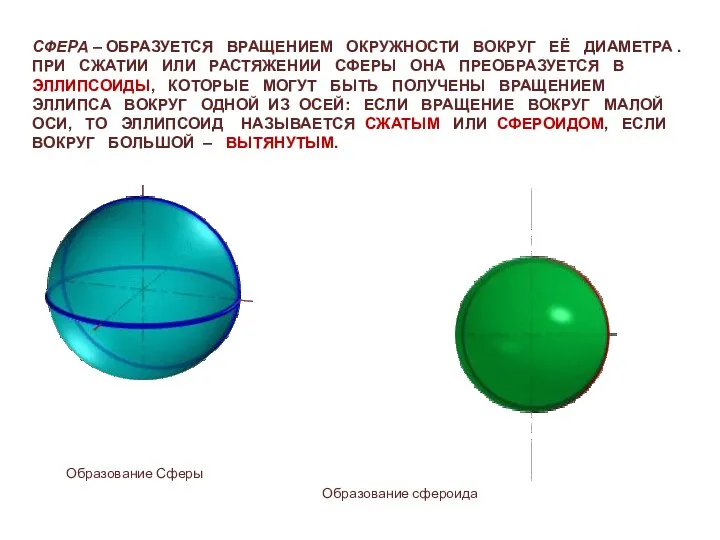
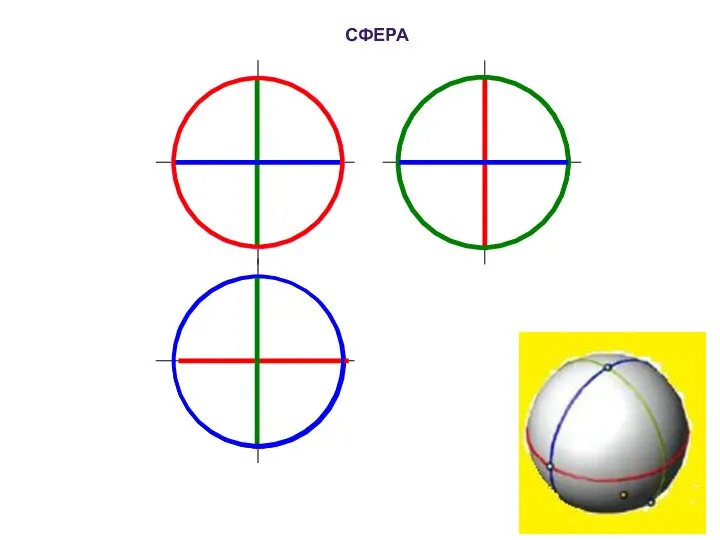
- 12. СФЕРА – ОБРАЗУЕТСЯ ВРАЩЕНИЕМ ОКРУЖНОСТИ ВОКРУГ ЕЁ ДИАМЕТРА . ПРИ СЖАТИИ ИЛИ РАСТЯЖЕНИИ СФЕРЫ ОНА ПРЕОБРАЗУЕТСЯ
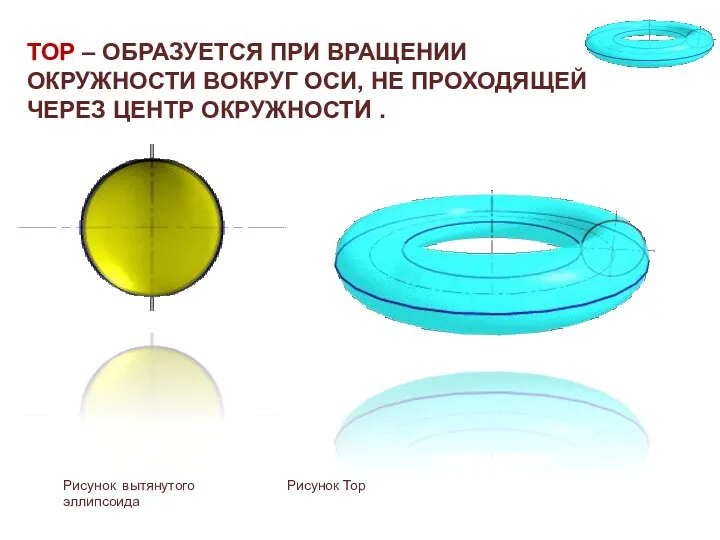
- 13. ТОР – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ОКРУЖНОСТИ ВОКРУГ ОСИ, НЕ ПРОХОДЯЩЕЙ ЧЕРЕЗ ЦЕНТР ОКРУЖНОСТИ . Рисунок вытянутого
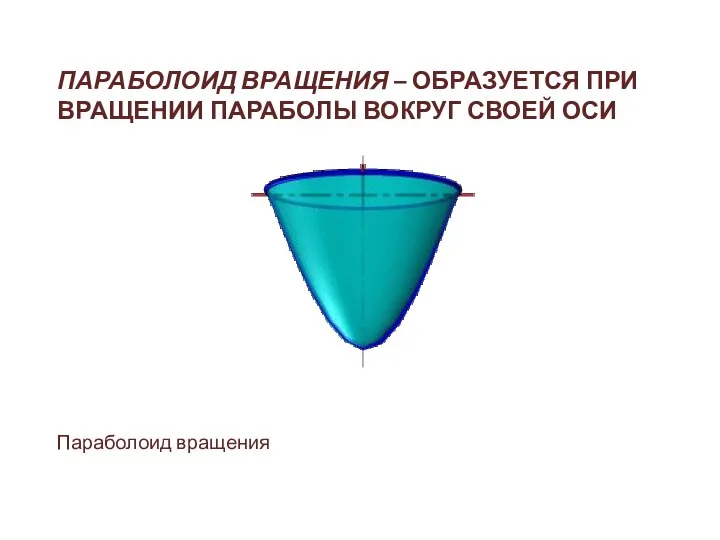
- 14. ПАРАБОЛОИД ВРАЩЕНИЯ – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ПАРАБОЛЫ ВОКРУГ СВОЕЙ ОСИ Параболоид вращения
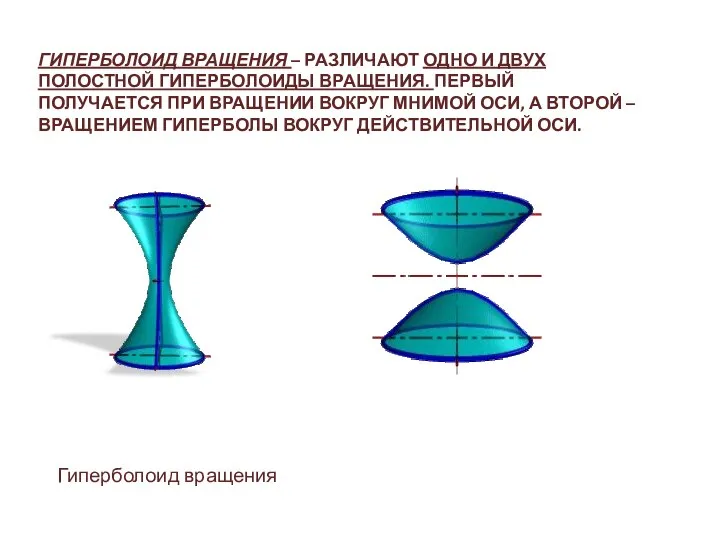
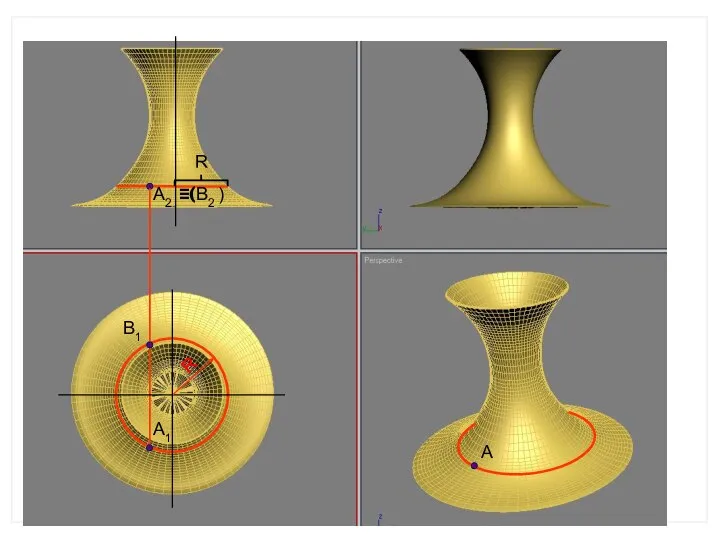
- 15. ГИПЕРБОЛОИД ВРАЩЕНИЯ – РАЗЛИЧАЮТ ОДНО И ДВУХ ПОЛОСТНОЙ ГИПЕРБОЛОИДЫ ВРАЩЕНИЯ. ПЕРВЫЙ ПОЛУЧАЕТСЯ ПРИ ВРАЩЕНИИ ВОКРУГ МНИМОЙ
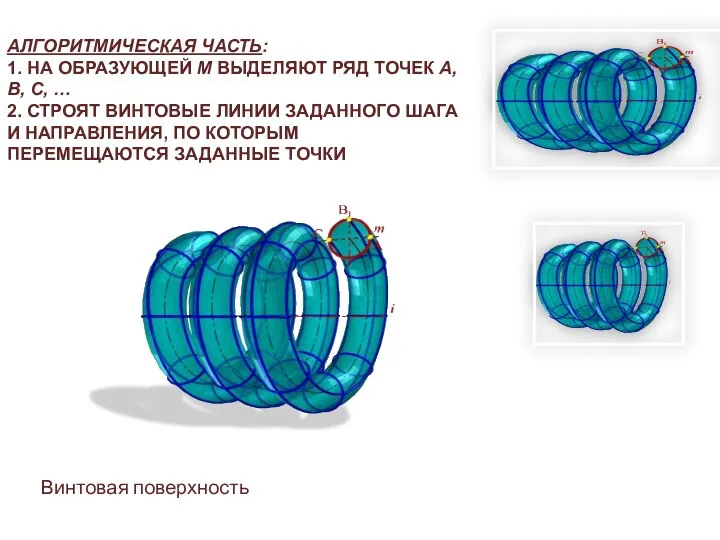
- 16. ВИНТОВЫЕ ПОВЕРХНОСТИ Винтовые поверхности образуются винтовым движением некоторой линии – образующей. Под винтовым движением понимается совокупность
- 17. АЛГОРИТМИЧЕСКАЯ ЧАСТЬ: 1. НА ОБРАЗУЮЩЕЙ M ВЫДЕЛЯЮТ РЯД ТОЧЕК А, В, С, … 2. СТРОЯТ ВИНТОВЫЕ
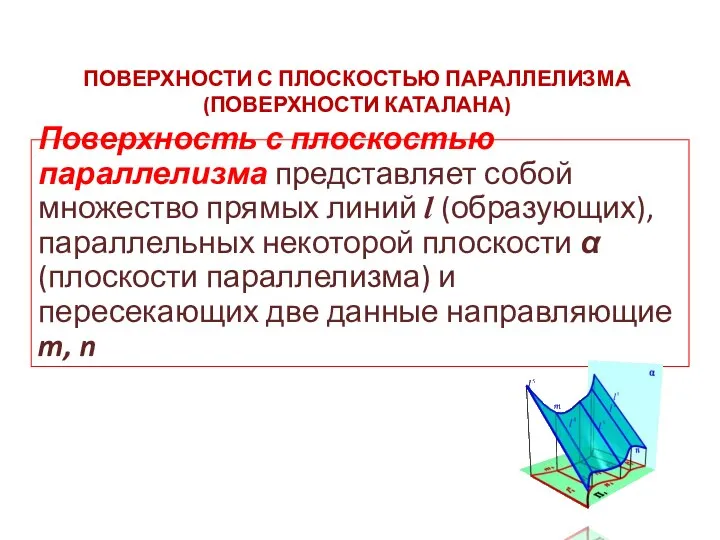
- 18. ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА (ПОВЕРХНОСТИ КАТАЛАНА) Поверхность с плоскостью параллелизма представляет собой множество прямых линий l
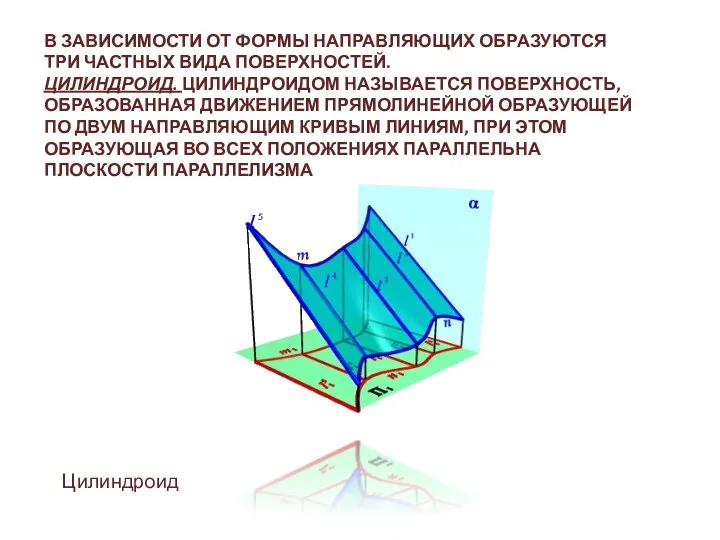
- 19. В ЗАВИСИМОСТИ ОТ ФОРМЫ НАПРАВЛЯЮЩИХ ОБРАЗУЮТСЯ ТРИ ЧАСТНЫХ ВИДА ПОВЕРХНОСТЕЙ. ЦИЛИНДРОИД. ЦИЛИНДРОИДОМ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ
- 20. КОНОИД. КОНОИДОМ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ ПО ДВУМ НАПРАВЛЯЮЩИМ, ОДНА ИЗ КОТОРЫХ КРИВАЯ ЛИНИЯ,
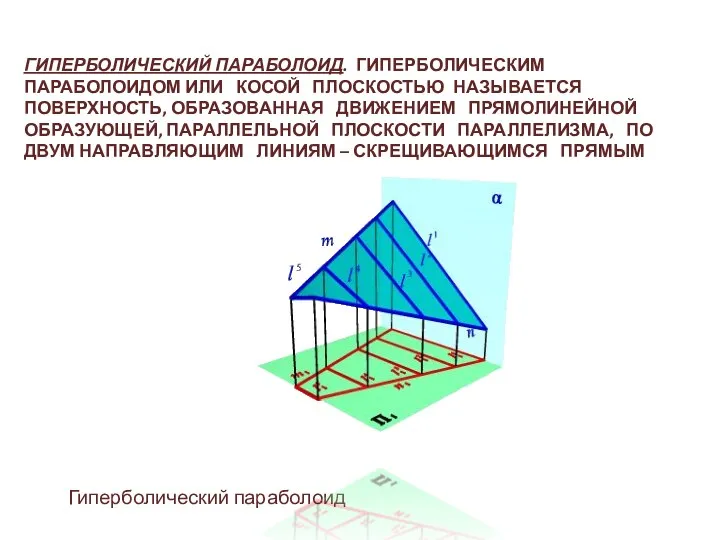
- 21. ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД. ГИПЕРБОЛИЧЕСКИМ ПАРАБОЛОИДОМ ИЛИ КОСОЙ ПЛОСКОСТЬЮ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ, ПАРАЛЛЕЛЬНОЙ ПЛОСКОСТИ ПАРАЛЛЕЛИЗМА,
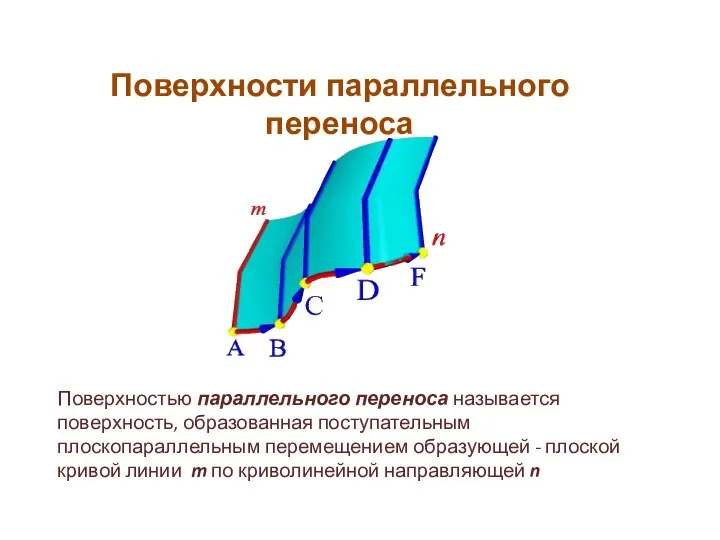
- 22. Поверхности параллельного переноса Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой
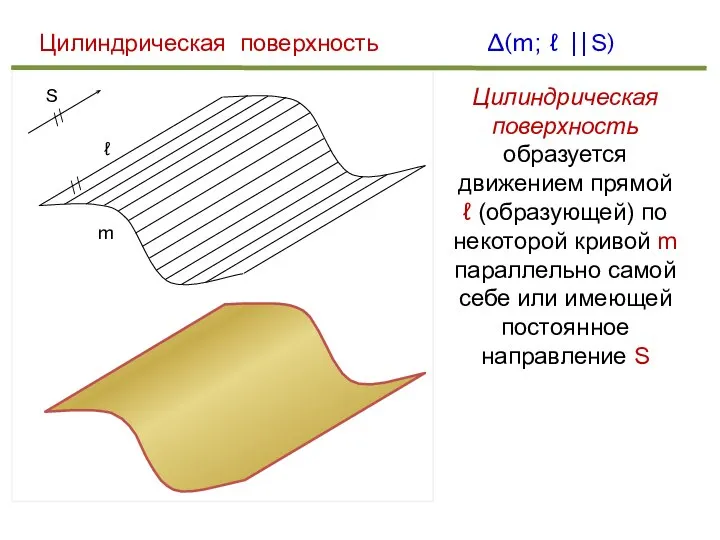
- 23. Цилиндрическая поверхность ℓ m ∆(m; ℓ ⎜⎜S) S // // Цилиндрическая поверхность образуется движением прямой ℓ
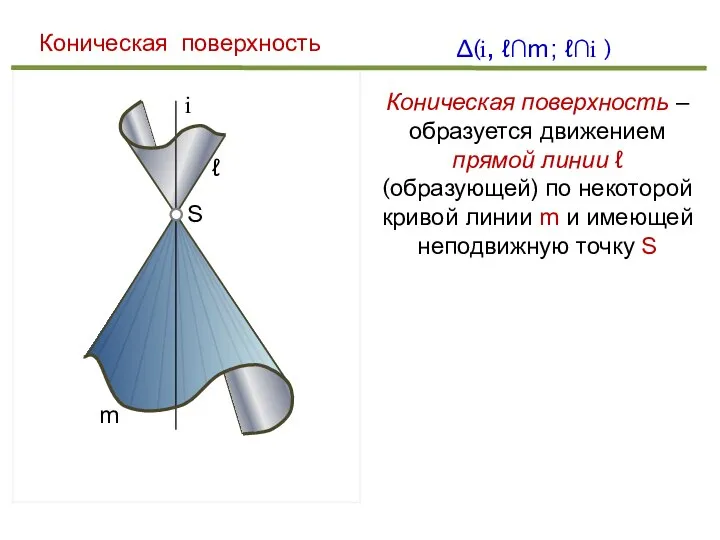
- 24. i m ℓ ∆(i, ℓ∩m; ℓ∩i ) Коническая поверхность Коническая поверхность – образуется движением прямой линии
- 25. Однополостный гиперболоид
- 26. Вогнутый тор (глобоид) Поверхность, образованная внутренней стороной вращающейся дуги радиусом R, называется глобоидом
- 27. R R А2 ≡(В2 ) А1 А В1
- 28. A2 (A1) Сфера
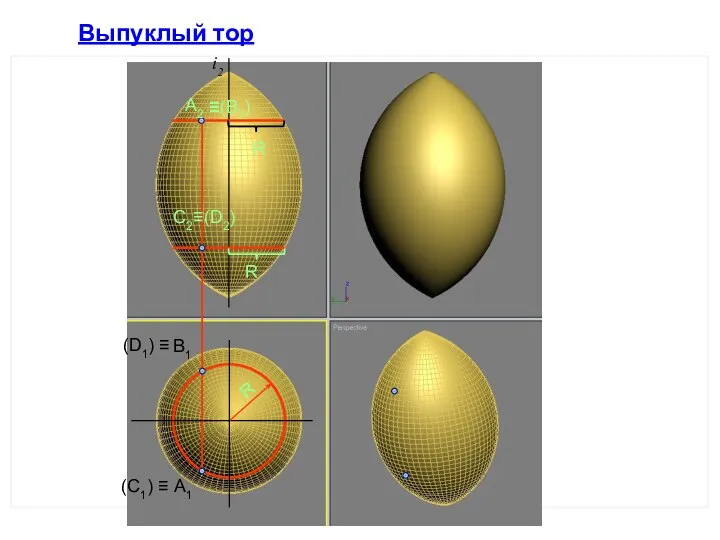
- 29. Выпуклый тор R R А2 А1 R В1 С2≡(D2) (C1) ≡ (D1) ≡ ≡(В2) i2
- 30. Эллипсоид
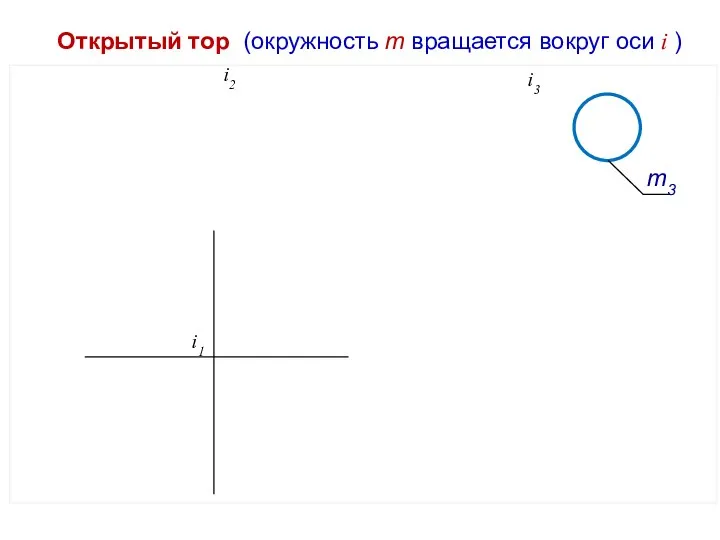
- 31. Открытый тор (окружность m вращается вокруг оси i ) i2 i1 i3 m3
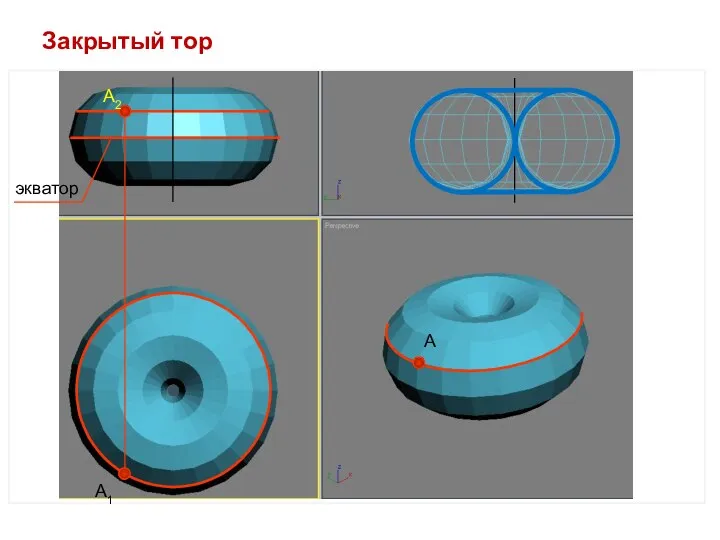
- 32. Закрытый тор А2 А1 А экватор
- 33. Закрытый кольцевой тор (самопересекающийся)
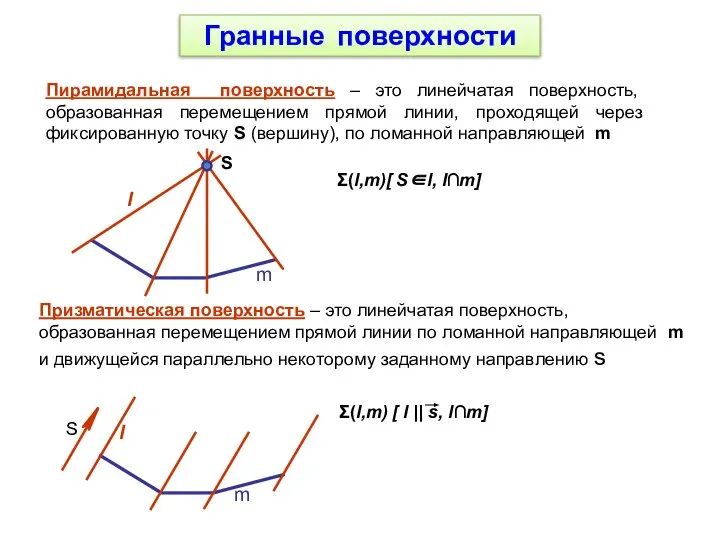
- 36. Гранные поверхности Пирамидальная поверхность – это линейчатая поверхность, образованная перемещением прямой линии, проходящей через фиксированную точку
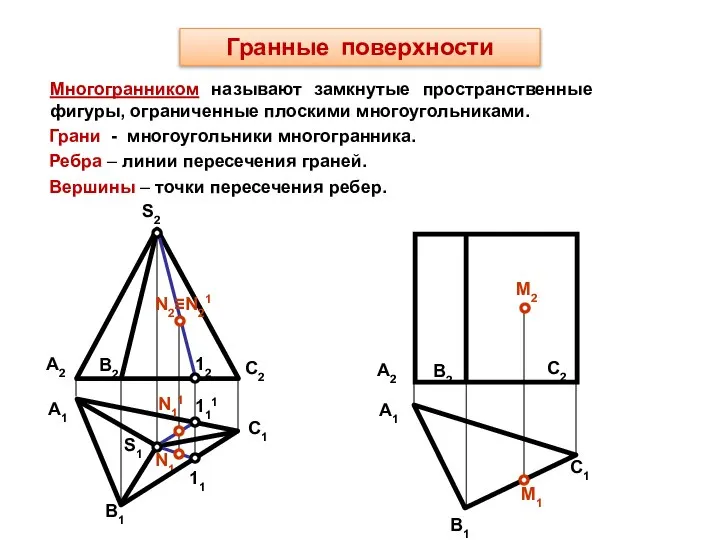
- 37. M1 А1 12 N1 S1 Гранные поверхности Многогранником называют замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. S2
- 38. Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей Многогранником называется тело, ограниченное многогранной поверхностью,
- 39. Построение проекций многогранника сводится к построению проекций его вершин и ребер.
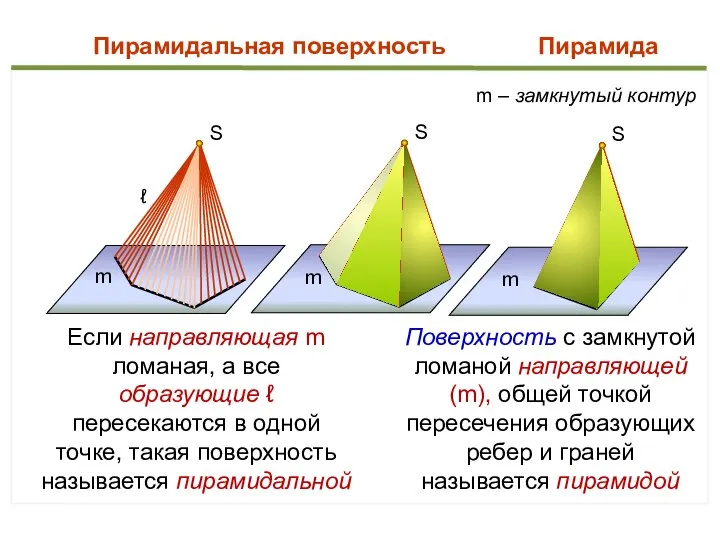
- 40. S ℓ m S m Пирамидальная поверхность S m Пирамида m – замкнутый контур Если направляющая
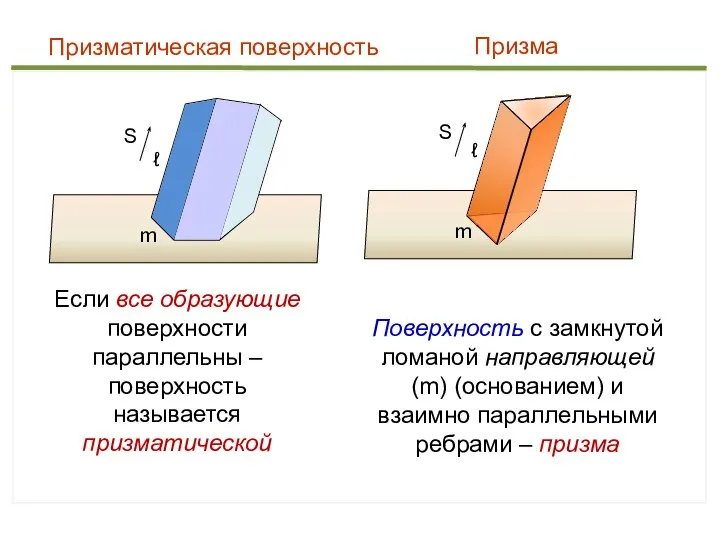
- 41. m S ℓ Призматическая поверхность m S ℓ Призма Если все образующие поверхности параллельны – поверхность
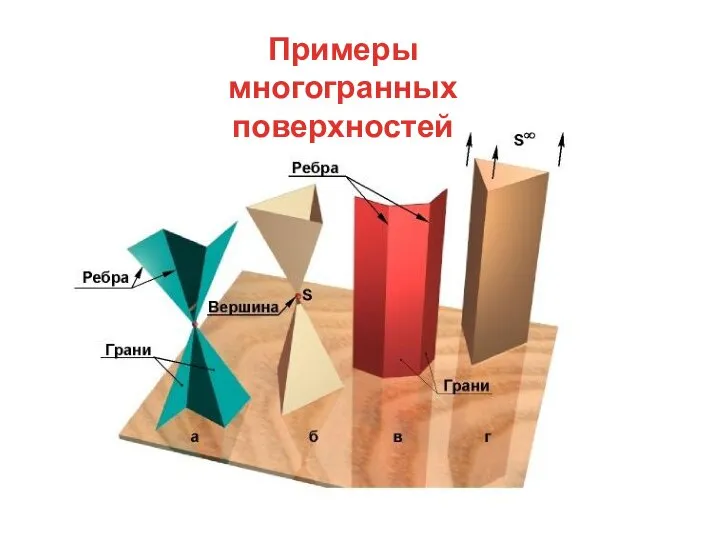
- 42. Примеры многогранных поверхностей
- 43. ПРАВИЛЬНЫЙ ШЕСТИГРАННИК (КУБ) ИЛИ ГЕКСАЭДР - ЧАСТНЫЙ СЛУЧАЙ ПРЯМОЙ ПРИЗМЫ, У КОТОРОЙ ОСНОВАНИЯ И БОКОВЫЕ ГРАНИ
- 44. ПРАВИЛЬНЫЙ ВОСЬМИГРАННИК ИЛИ ОКТАЭДР - МНОГОГРАННИК, СОСТОЯЩИЙ ИЗ ВОСЬМИ ГРАНЕЙ - ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ, СОЕДИНЕННЫХ ПО ЧЕТЫРЕ
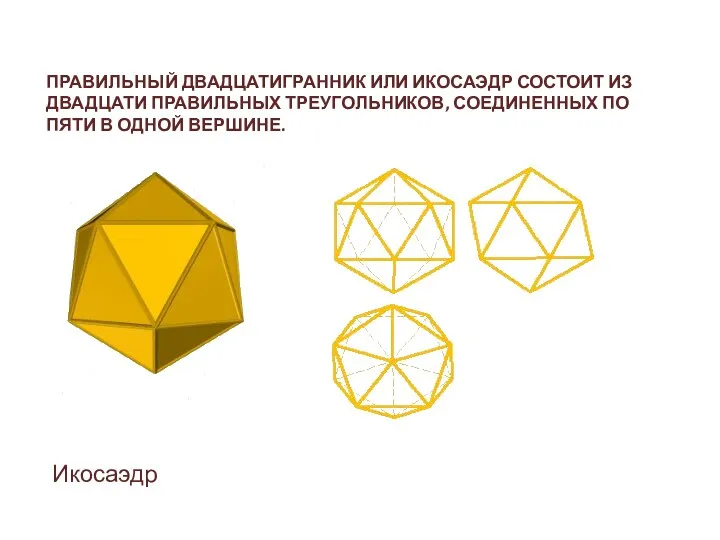
- 45. ПРАВИЛЬНЫЙ ДВАДЦАТИГРАННИК ИЛИ ИКОСАЭДР СОСТОИТ ИЗ ДВАДЦАТИ ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ, СОЕДИНЕННЫХ ПО ПЯТИ В ОДНОЙ ВЕРШИНЕ. Икосаэдр
- 46. Призматоид
- 47. Следует запомнить: Проекции точек , принадлежащих поверхности геометрического тела, располагаются на линиях очерка и внутри его,
- 48. Построение точки на поверхности многогранника: в плоскости грани проводят прямую и на этой прямой находят точку.
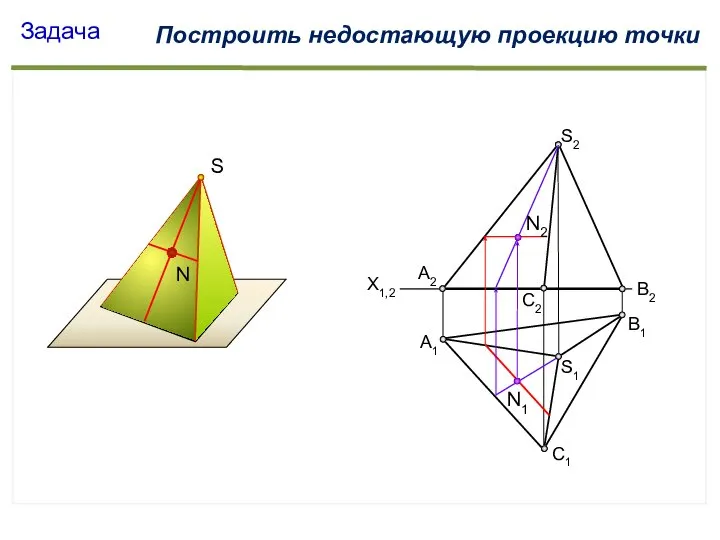
- 49. S А1 С1 В1 S2 X1,2 S1 А2 С2 В2 Задача Построить недостающую проекцию точки N
- 50. Поверхности вращения
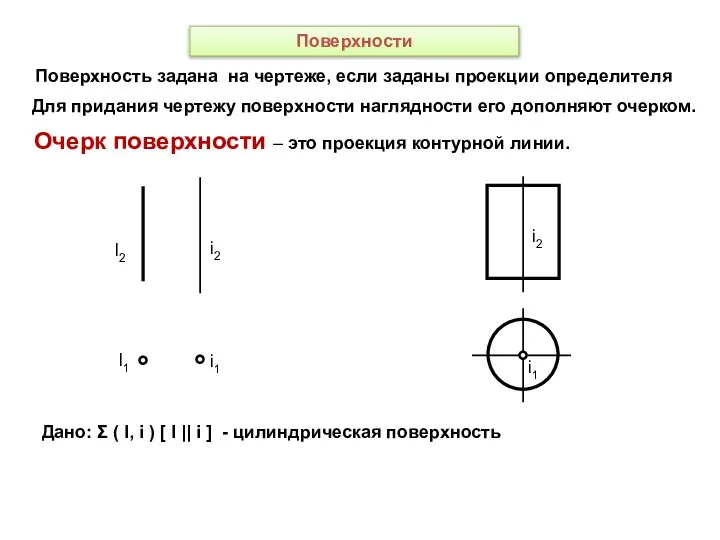
- 51. Поверхности Поверхность задана на чертеже, если заданы проекции определителя i2 i1 l2 l1 Для придания чертежу
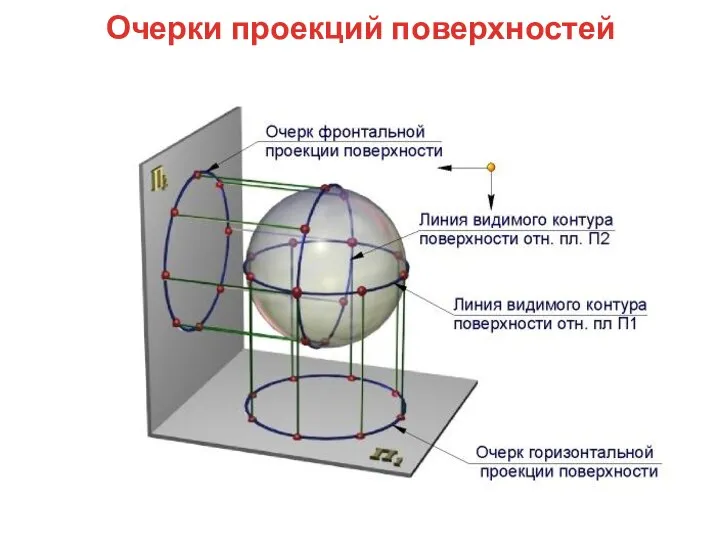
- 52. Очерки проекций поверхностей
- 53. Линии, образующие внешний контур геометрического тела, называют О Ч Е Р К О М . Различают
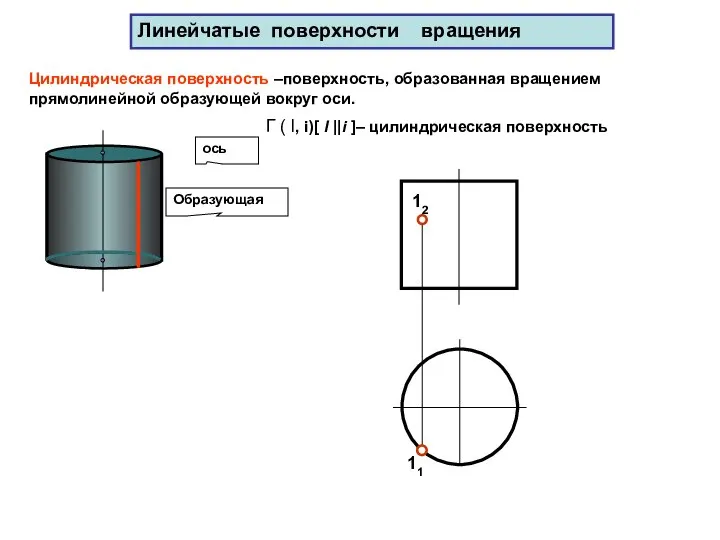
- 54. 12 11 Цилиндрическая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг оси. Г ( l, i)[ l
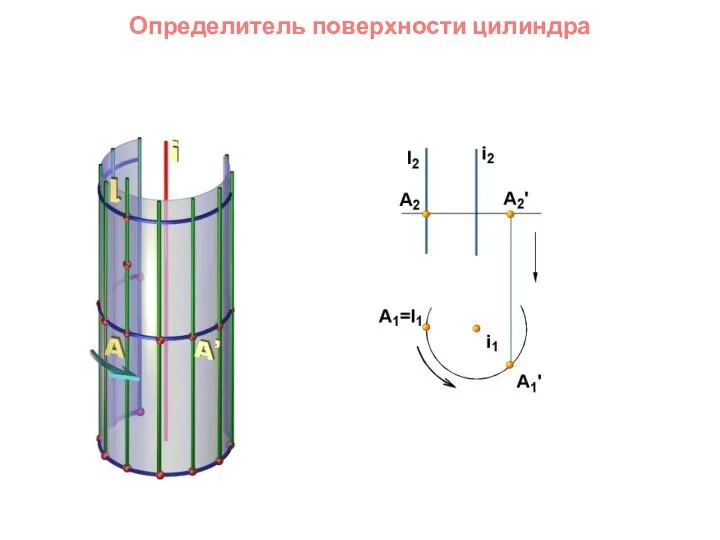
- 55. Определитель поверхности цилиндра
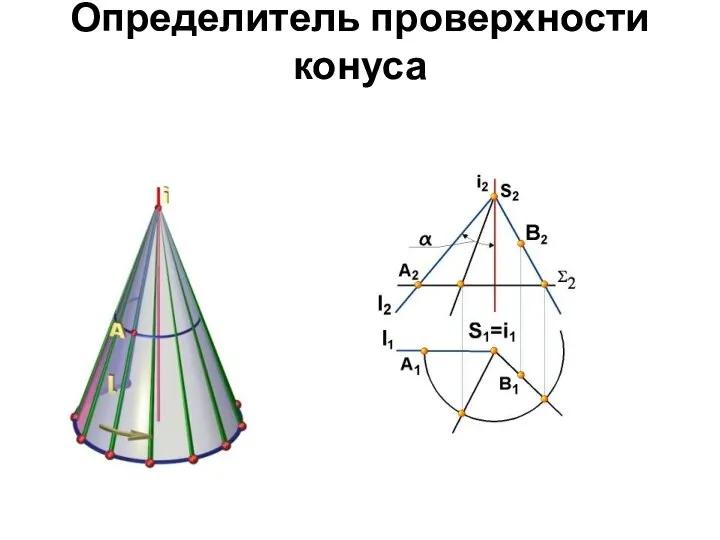
- 56. Определитель проверхности конуса
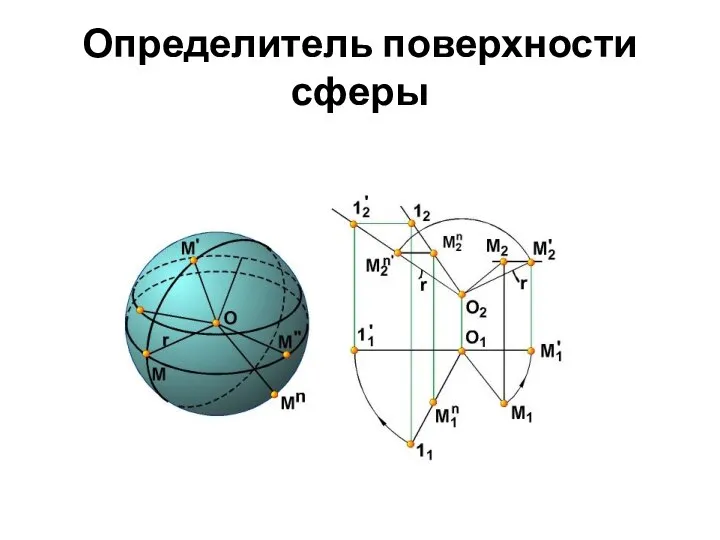
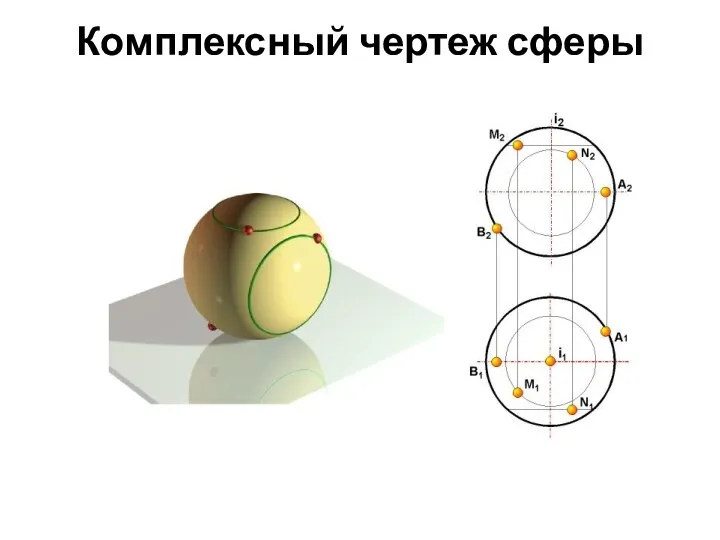
- 57. Определитель поверхности сферы
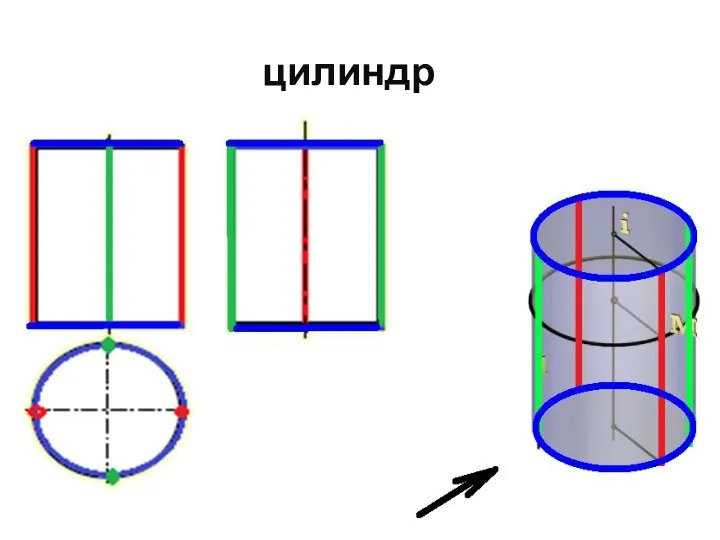
- 58. цилиндр
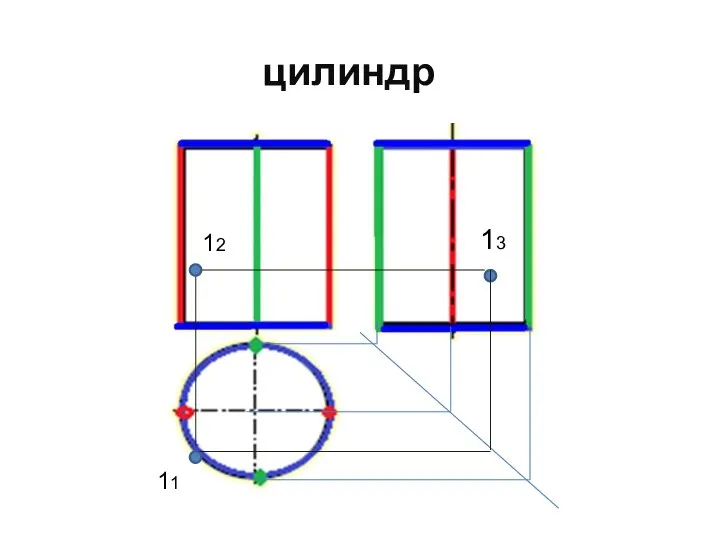
- 59. цилиндр 13 11 12
- 62. Точка принадлежит поверхности, если она принадлежит линии, расположенной на этой поверхности Линия принадлежит поверхности, если каждая
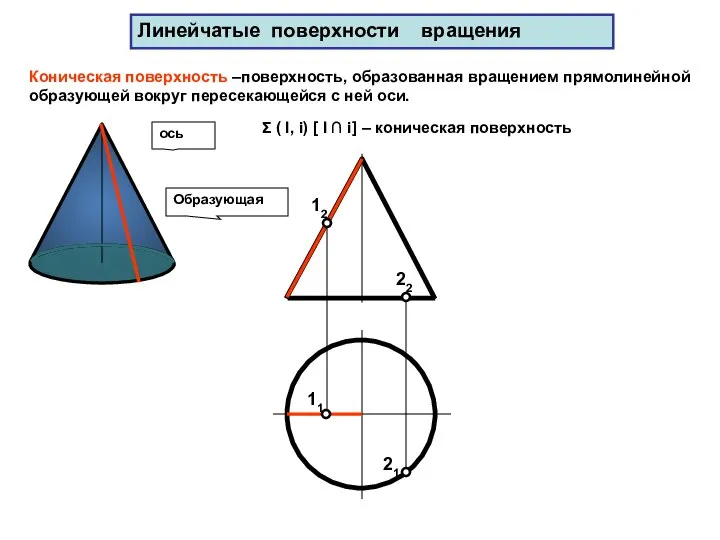
- 63. Линейчатые поверхности вращения Коническая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг пересекающейся с ней оси. Образующая
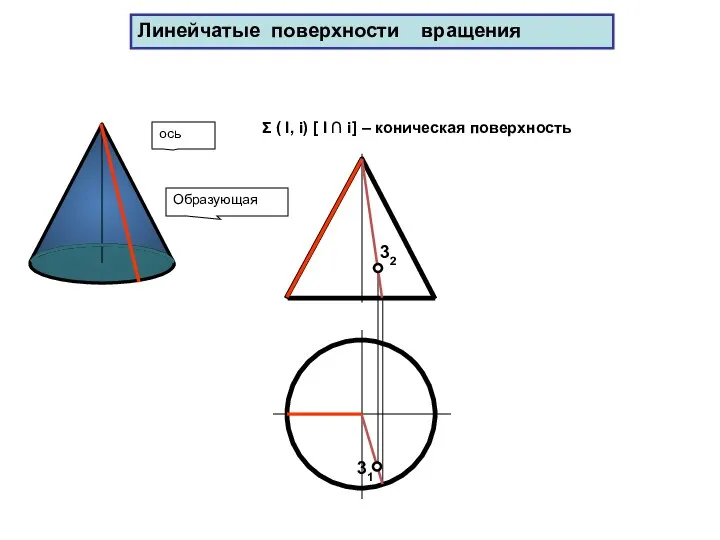
- 64. 31 Образующая ось 32 Σ ( l, i) [ l ∩ i] – коническая поверхность Линейчатые
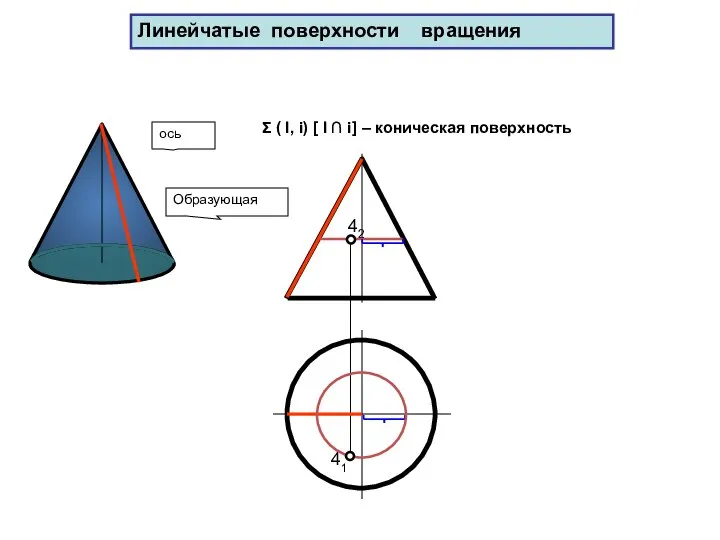
- 65. 41 Образующая ось 42 Σ ( l, i) [ l ∩ i] – коническая поверхность Линейчатые
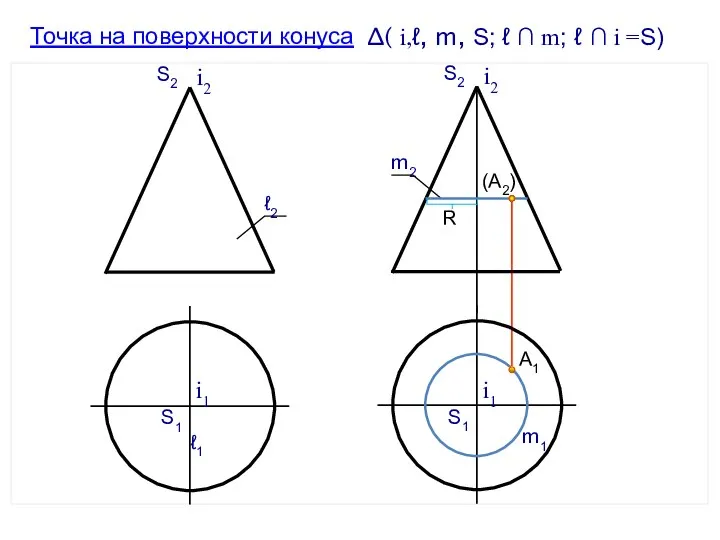
- 67. А2 А1 i2 S2 ∆( i,ℓ, m, S; ℓ ∩ m; ℓ ∩ i =S) ℓ2
- 68. СФЕРА
- 69. Комплексный чертеж сферы
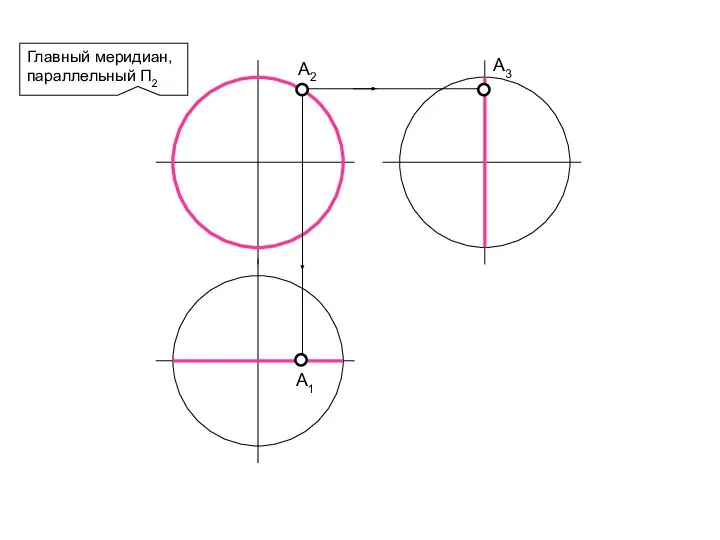
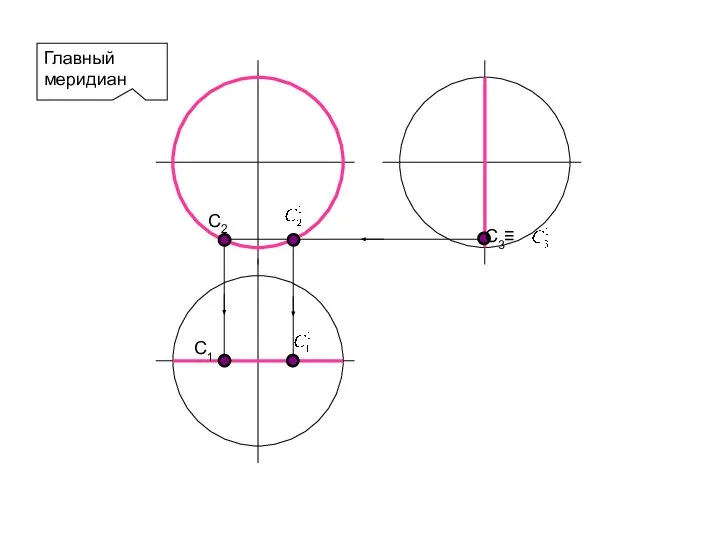
- 70. Главный меридиан, параллельный П2 А2 А1 А3
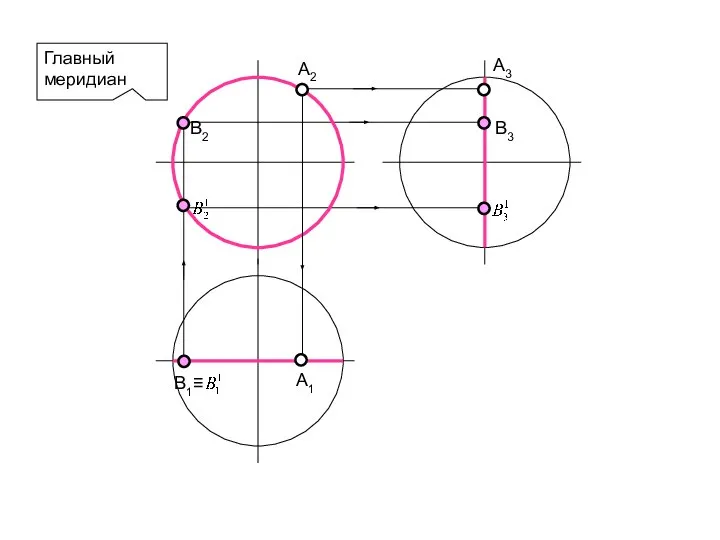
- 71. Главный меридиан В2 В3
- 72. Главный меридиан C1 C2
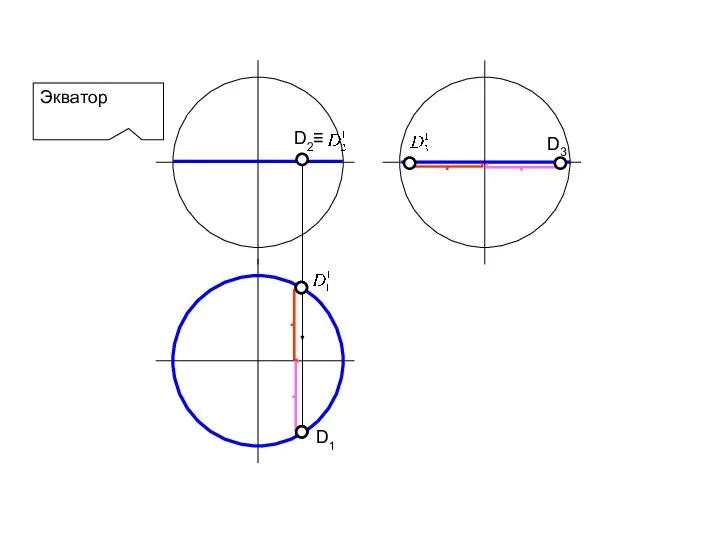
- 73. Экватор D1 D3
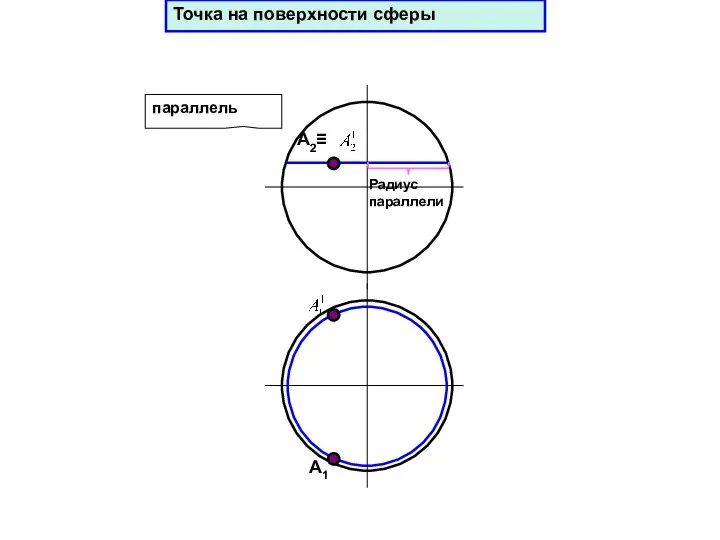
- 74. А1 параллель Радиус параллели Точка на поверхности сферы
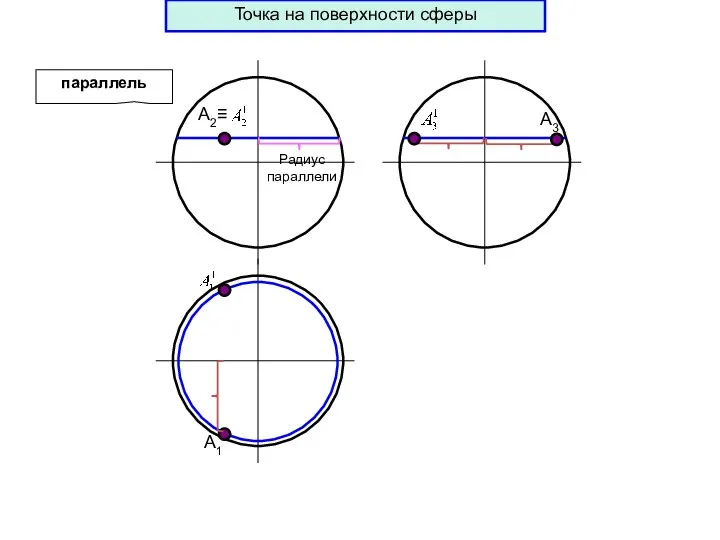
- 75. А1 параллель А3 Радиус параллели Точка на поверхности сферы
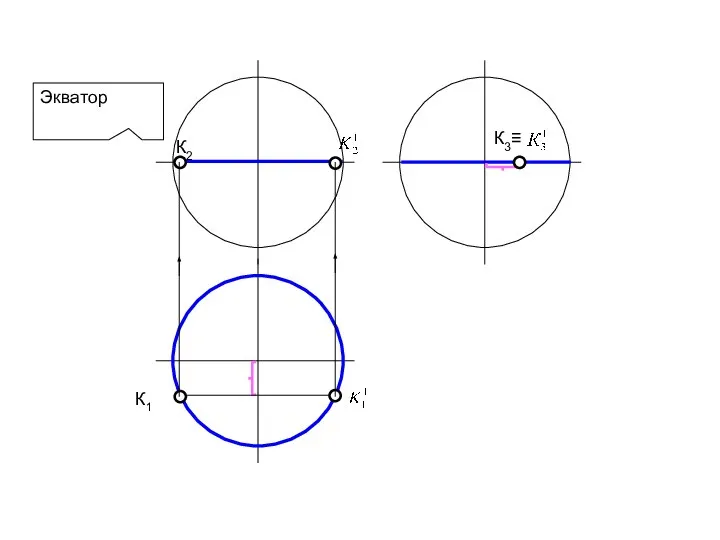
- 76. Экватор К1
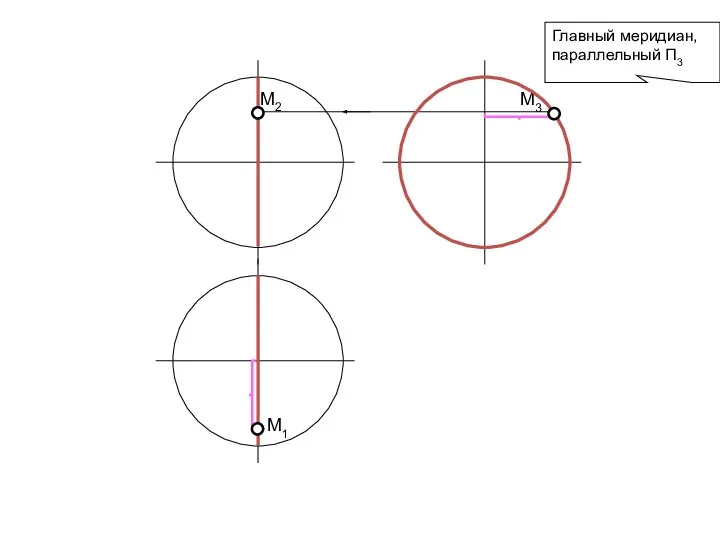
- 77. Главный меридиан, параллельный П3 М3 М2 М1
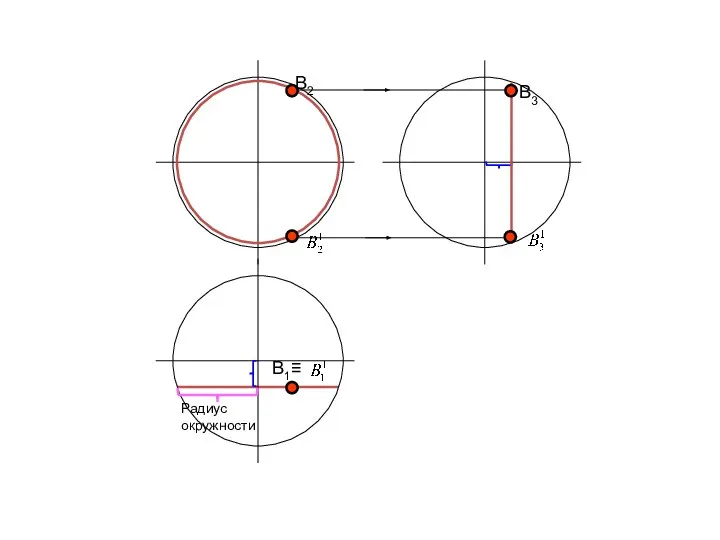
- 78. Радиус окружности
- 79. Радиус окружности
- 80. Обычно геометрические тела изображаются в их простейших положениях, наиболее выгодных для проецирования, когда оси, образующие, ребра
- 81. ***Построение комплексных чертежей начинают с тех плоскостей проекций, на которые их основания проецируются в натуральную величину.
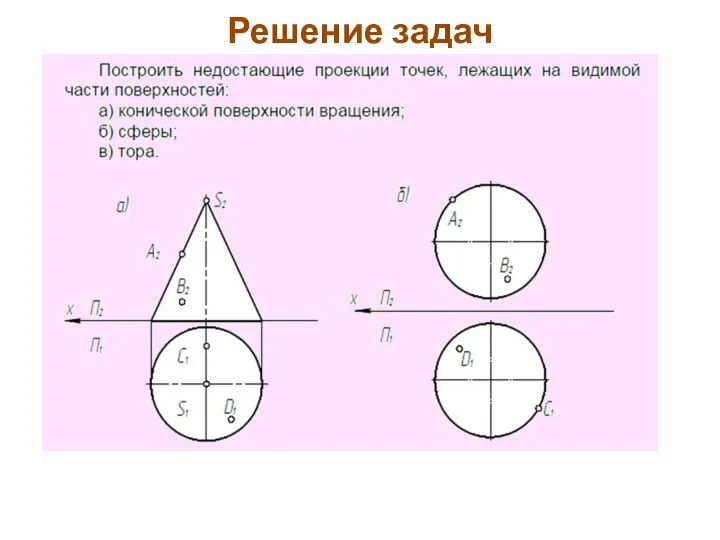
- 82. Решение задач
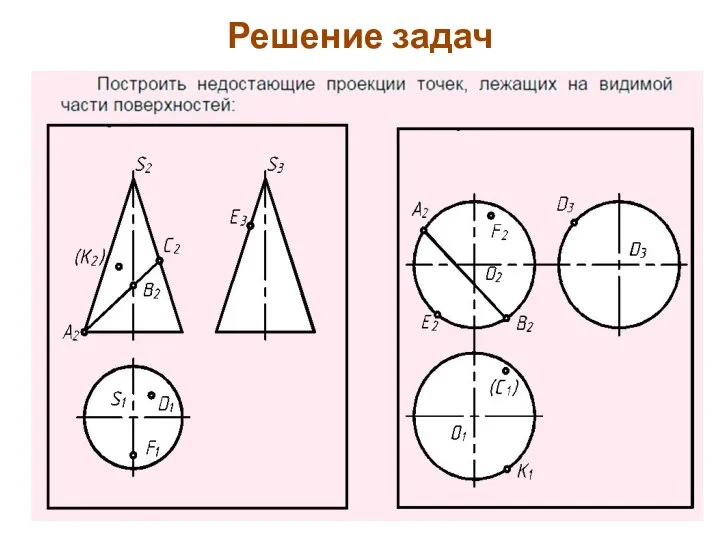
- 83. Решение задач
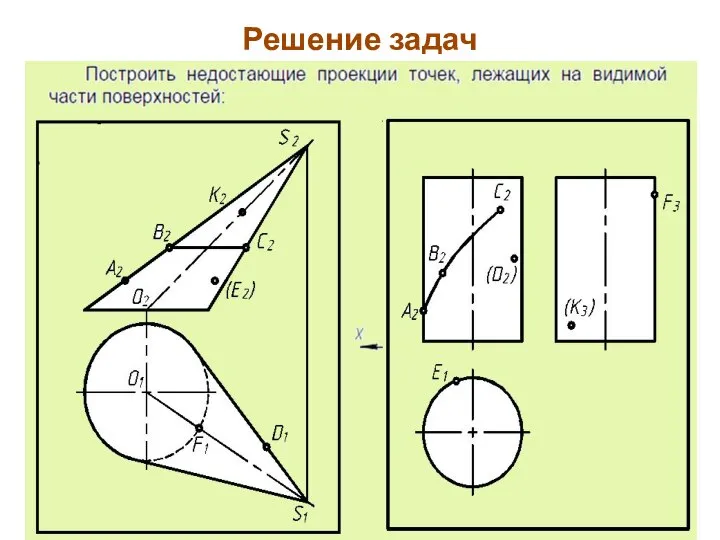
- 84. Решение задач
- 86. Скачать презентацию





























 Пневмонии и гнойные заболевания лёгких. Этиология. Клиника. Диагностика. Осложнения. Основные принципы лечения Доцент Т.Ю.Че
Пневмонии и гнойные заболевания лёгких. Этиология. Клиника. Диагностика. Осложнения. Основные принципы лечения Доцент Т.Ю.Че Презентация на тему "Лёгкие в лучевом изображении и лучевые синдромы заболеваний лёгких" - скачать презентации по Медицине
Презентация на тему "Лёгкие в лучевом изображении и лучевые синдромы заболеваний лёгких" - скачать презентации по Медицине Дозирование нагрузки при занятиях бегом. Легкоатлетическая гимнастика
Дозирование нагрузки при занятиях бегом. Легкоатлетическая гимнастика Облік розрахунків з дебіторами
Облік розрахунків з дебіторами Исследовательская работа «Кристаллы. Выращивание кристаллов». Выполнили ученицы 8 класса Печниковской средней школы Каргопольс
Исследовательская работа «Кристаллы. Выращивание кристаллов». Выполнили ученицы 8 класса Печниковской средней школы Каргопольс Процесс управления и управленческие решения
Процесс управления и управленческие решения Объектно-ориентированное проектирование ПС (часть 2)
Объектно-ориентированное проектирование ПС (часть 2) Лингвистические особенности речи политических лидеров (на примере предвыборных речей Барака Обамы и Дональда Трампа)
Лингвистические особенности речи политических лидеров (на примере предвыборных речей Барака Обамы и Дональда Трампа) Гаджеты в жизни ребёнка
Гаджеты в жизни ребёнка Планирование процесса исследования систем управления: основные понятия и организация работы
Планирование процесса исследования систем управления: основные понятия и организация работы Театр моды "Силуэт"
Театр моды "Силуэт" Eвропейский стандарт цифрового эфирного телевидения DVB-T2
Eвропейский стандарт цифрового эфирного телевидения DVB-T2 Реформы Петра І и судьбы российской и украинской художественной культуры
Реформы Петра І и судьбы российской и украинской художественной культуры Поверхности. Способы задания поверхности
Поверхности. Способы задания поверхности Основы аудита
Основы аудита  Шестипульсовая (трехфазная) мостовая схема управляемого выпрямителя
Шестипульсовая (трехфазная) мостовая схема управляемого выпрямителя Презентацию подготовил ученик 8 класса Ерошенко Григорий
Презентацию подготовил ученик 8 класса Ерошенко Григорий Аграрный календарь. Обычаи и обряды. Праздничность. Игра Часть 4
Аграрный календарь. Обычаи и обряды. Праздничность. Игра Часть 4 Общая патология клетки 2
Общая патология клетки 2 Политический конфликт
Политический конфликт Великобритания (Политическая система, образование, культура и традиции)
Великобритания (Политическая система, образование, культура и традиции) Презентация Академические звания
Презентация Академические звания Свойства операций
Свойства операций  Стандарты финансовой отчетности
Стандарты финансовой отчетности  Культура адыгских народов
Культура адыгских народов Творческие работы учащихся 4 класса Учитель Шутова Марина Викторовна
Творческие работы учащихся 4 класса Учитель Шутова Марина Викторовна Relational Algebra
Relational Algebra Маркетинговое исследование предпочтений потребителей печенья «Юбилейное» Юрлова Виктория, ДС.02
Маркетинговое исследование предпочтений потребителей печенья «Юбилейное» Юрлова Виктория, ДС.02