Содержание
- 2. Цель работы: Закрепление изученного материала по теме «Производная» и ознакомление с её прикладной частью.
- 3. План работы: 1.Исследование функции на монотонность 2.Касательная к графику. 3.Наибольшие, наименьшие значения функций. 4.Нахождение дифференциала для
- 4. Определение производной Производной данной функции в точке х называется предел отношения приращения этой функции к приращению
- 5. . Будем считать, что рассматриваемая функция y=f(x) определена и дифференцируема в каждой точке отрезка a ≤
- 6. Решение: Чтобы применить признаки возрастания и убывания функции, найдем производную данной функции и определим значения х,
- 7. Вообразим, что на кривой АВ точка М неограниченно приближается к неподвижной точке С, секущая СМ при
- 8. Определение. Прямая СТ, предельное положение секущей СМ, называется касательной к кривой в точке С. Точка С
- 9. ∙ Задача . Найдите площадь треугольника AMB, если A и B — точки пересечения с осью
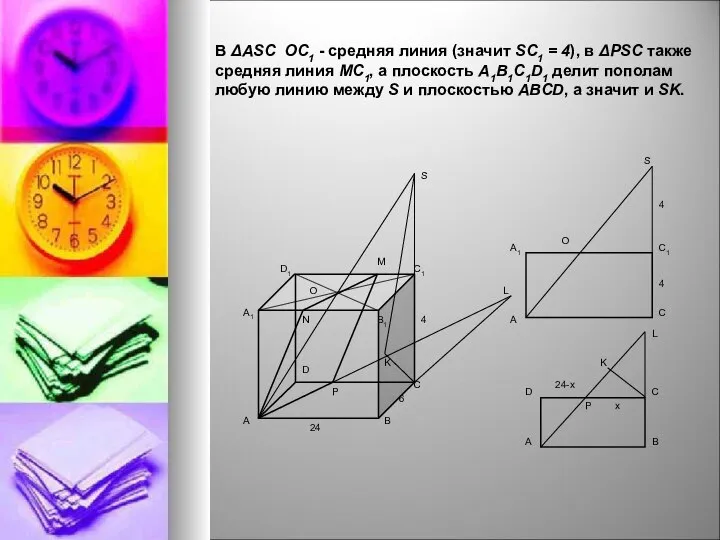
- 10. Задача . В прямоугольном параллелепипеде ABCDA1B1C1D1 с ребрами CD = 24, AD= 6 и DD1 =4
- 11. В ΔASC ОC1 - средняя линия (значит SC1 = 4), в ΔPSC также средняя линия МC1,
- 12. Пусть PC = x; ΔCLP подобен ΔDАР LC/AD = x/(24—x), LC = 6x/(24 – x). Из
- 13. 4.Нахождение дифференциала для приближенных вычислений. Определение. Дифференциалом (dy) функции y=f(x) называется произведение значения производной f '(х)
- 14. Пример: Вычислить приближенно с помощью дифференциала. . В нашем случае: , , . Вычисляем: ; ,
- 15. Если функция f имеет положительную (отрицательную) производную в каждой точке некоторого промежутка, то она возрастает (убывает)
- 17. Скачать презентацию













 Ремонт деталей машин с применением полимерных материалов
Ремонт деталей машин с применением полимерных материалов Презентация Налог на прибыль
Презентация Налог на прибыль СТИЛИСТИКА АНГЛИЙСКОГО ЯЗЫКА ENGLISH STYLISTICS
СТИЛИСТИКА АНГЛИЙСКОГО ЯЗЫКА ENGLISH STYLISTICS МФ РФ_ДПРБО_Саакян Т.В._НПР полномочий ФК
МФ РФ_ДПРБО_Саакян Т.В._НПР полномочий ФК Пантеизм и новая космология
Пантеизм и новая космология Презентация Восточный и западный типы культур
Презентация Восточный и западный типы культур Йоль. Символика Йоля
Йоль. Символика Йоля Математика 1 класс На что похожа цифра Презентацию выполнила учитель начальных классов МОУ СОШ с Урицкое Николаева Е.В.
Математика 1 класс На что похожа цифра Презентацию выполнила учитель начальных классов МОУ СОШ с Урицкое Николаева Е.В. ПРОСЛАВЛЕНИЕ 08.09.2019
ПРОСЛАВЛЕНИЕ 08.09.2019 Пневматическое оборудование трамвайных вагонов
Пневматическое оборудование трамвайных вагонов Масленица и её традиции
Масленица и её традиции Интерфейс
Интерфейс Introduction to Java Web
Introduction to Java Web Лоренцо Романо Амедео Карло Авогадро ді Кваренья е ді Черретто
Лоренцо Романо Амедео Карло Авогадро ді Кваренья е ді Черретто Долговечность бетона. Однородность бетона
Долговечность бетона. Однородность бетона Смета ремонта комнаты
Смета ремонта комнаты Маркетинг социальных услуг Автор: ученица 10 «а» класса Затинацкая Ксения Научный руководитель: социальный педагог, магист
Маркетинг социальных услуг Автор: ученица 10 «а» класса Затинацкая Ксения Научный руководитель: социальный педагог, магист Рекомендации для учителя ДО
Рекомендации для учителя ДО Противоправное деяние. Преступление
Противоправное деяние. Преступление Проект. Спортивный комплекс с батутным центром и скалодромом
Проект. Спортивный комплекс с батутным центром и скалодромом Образовательная программа: теория и технология конструирования
Образовательная программа: теория и технология конструирования Создание тендерного отдела
Создание тендерного отдела Биография Антуана де Сент-Экзюпери
Биография Антуана де Сент-Экзюпери  Натюрморт
Натюрморт Свойства операций
Свойства операций  ЗДОРОВОЕ ПИТАНИЕ
ЗДОРОВОЕ ПИТАНИЕ Гроші. Їх види
Гроші. Їх види Принципы физического воспитания. Условия здорового образа жизни
Принципы физического воспитания. Условия здорового образа жизни