Работу выполнили: Сидорова Анжела Соловьева Наталья Захарова Ольга Сафонова Виктория Пискунова Наталья Руководитель: Елоев
Содержание
- 2. ОГЛАВЛЕНИЕ Титульная страница Оглавление Вступление Предел переменной величины Основные свойства пределов Предел функции в точке Понятие
- 3. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ Предел – одно из основных понятий математического анализа. Понятие предела использовалось еще Ньютоном
- 4. 1. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ Пусть переменная величина x в процессе своего изменения неограниченно приближается к числу
- 5. 2. ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ 1. Предел алгебраической суммы конченного числа переменных величин равен алгебраической сумме пределов
- 6. 3.ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ Определение 2. Число b называется пределом* функции в точке a, если для
- 7. 4. ПОНЯТИЕ О НЕПРЕРЫВНОСТИ ФУНКЦИИ 2. Вычислить Решение. При x = 1 дробь определена, так как
- 8. 5. ПРЕДЕЛ ФУНКЦИИ НА БЕСКОНЕЧНОСТИ 3.Найти Решение. При x знаменатель х + 5 также стремится к
- 9. 6. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ Некоторые пределы невозможно найти теми способами, которые были изложены выше. Пусть например, требуется
- 10. 7. ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ 1. (x2 – 7x + 4) = 32 – 7·3 + 4 =
- 12. Скачать презентацию









 Развития русского театра в XIX-XX веках
Развития русского театра в XIX-XX веках Международная статистическая классификация болезней и проблем, связанных со здоровьем 10 пересмотра
Международная статистическая классификация болезней и проблем, связанных со здоровьем 10 пересмотра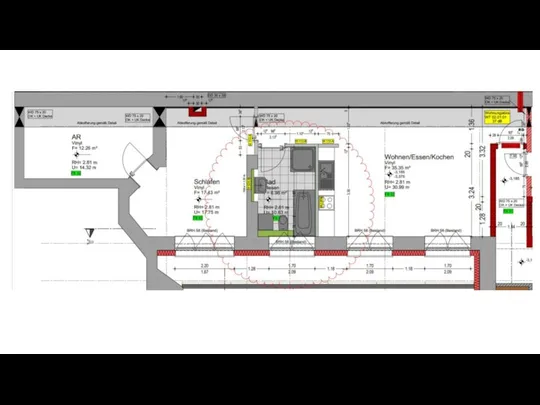 План первого этажа здания
План первого этажа здания Волшебная петриковская роспись Методист Колесникова Марина Леонидовна
Волшебная петриковская роспись Методист Колесникова Марина Леонидовна Вожо - зимний обряд бесермян
Вожо - зимний обряд бесермян Взаимосвязи систем и устройств стенда для исследования физико-механических свойств ядерного топлива
Взаимосвязи систем и устройств стенда для исследования физико-механических свойств ядерного топлива Терроризм. Из истории терроризма
Терроризм. Из истории терроризма Местная анестезия
Местная анестезия Костюмы Древнего Египта
Костюмы Древнего Египта Балки и прогоны цельного сечения. Составные балки на податливых связях
Балки и прогоны цельного сечения. Составные балки на податливых связях Чернильная система
Чернильная система Trend Hunter Цвет поиск деньги
Trend Hunter Цвет поиск деньги Резьба, её образование, параметры, классификация резьб
Резьба, её образование, параметры, классификация резьб Физкультурно-спортивный клуб «Норд» Варгашинский район село Верхнесуерское
Физкультурно-спортивный клуб «Норд» Варгашинский район село Верхнесуерское Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Сценарное планирование в современном стратегическом менеджменте
Сценарное планирование в современном стратегическом менеджменте Административные правонарушения, посягающие на нормальную деятельность таможенных органов
Административные правонарушения, посягающие на нормальную деятельность таможенных органов ПОЗИЦИОНИРОВАНИЕ HTML-элементов Web-страницы С ИСПОЛЬЗОВАНИЕМ CSS-СТИЛЕЙ
ПОЗИЦИОНИРОВАНИЕ HTML-элементов Web-страницы С ИСПОЛЬЗОВАНИЕМ CSS-СТИЛЕЙ Природа и сущность государственного и муниципального управления. (Тема 1)
Природа и сущность государственного и муниципального управления. (Тема 1) Второй цикл семинаров по медиаобразованию и духовно-нравственному воспитанию для преподавателей Тверского региона
Второй цикл семинаров по медиаобразованию и духовно-нравственному воспитанию для преподавателей Тверского региона Бершадська загальноосвітня школа І-ІІІ ступенів №3 Початкова школа
Бершадська загальноосвітня школа І-ІІІ ступенів №3 Початкова школа Методы изучения наследственности человека
Методы изучения наследственности человека  Методы минимизации рисков
Методы минимизации рисков Оқушылардың өзін-өзі басқару жүйесінің әдістемесі
Оқушылардың өзін-өзі басқару жүйесінің әдістемесі Пейзаж в литературе, музыке, живописи.
Пейзаж в литературе, музыке, живописи.  Гидроплазма Water For Life
Гидроплазма Water For Life Введение в язык программирования С++
Введение в язык программирования С++ Примерная основная образовательная программа начального общего образования: цель, назначение, структура
Примерная основная образовательная программа начального общего образования: цель, назначение, структура