Распределение напряжений в грунтовом массиве и принцип линейной деформируемости грунтов (задачи Буссинеска, Лява, Фламана)
Содержание
- 2. ФАКТОРЫ, ВЛИЯЮЩИЕ НА НАПРЯЖЕНИЯ В ГРУНТЕ: инженерно-геологические и гидрогеологические условия строительной площадки; физико-механические свойства грунтов; глубина
- 3. ОСНОВНЫЕ РЕАЛЬНЫЕ ОСОБЕННОСТИ ГРУНТА: является неупругим материалом; является несплошным телом; является анизотропным телом (с отличающимися напряжениями
- 6. Но… действующие нормативные документы рекомендуют использовать для решения задач механики грунтов законы теории упругости, которые применяют
- 7. При решении задач расчета и оценки напряженно-деформированного состояния грунт рассматривают как сплошную среду без учета промежутков
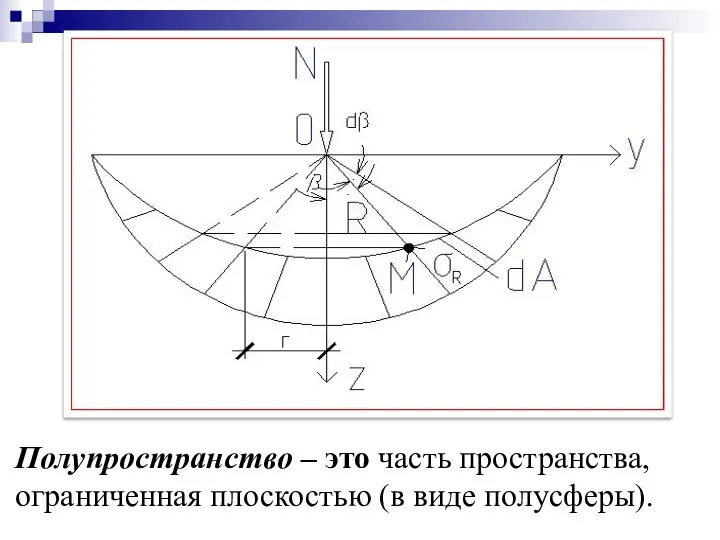
- 8. Полупространство – это часть пространства, ограниченная плоскостью (в виде полусферы).
- 10. ПРИНЦИП ЛИНЕЙНОЙ ДЕФОРМИРУЕМОСТИ заключается в допущении линейной связи между напряжениями и деформациями и формулируется так: при
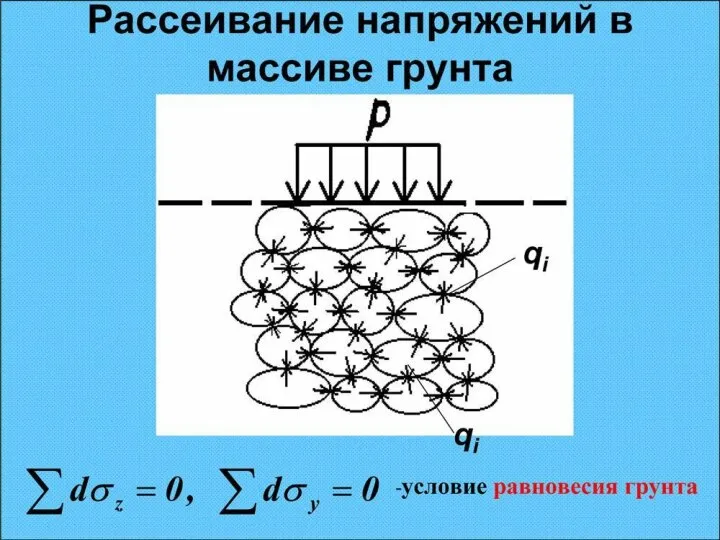
- 11. Определение напряжений в массиве грунта Грунт обладает зернистостью и анизотропностью, но условно принимается, что грунт является
- 12. Однако, если разгрузить штамп после уплотнения грунта основания нагрузкой N, еще не вызвавшей интенсивных местных сдвигов,
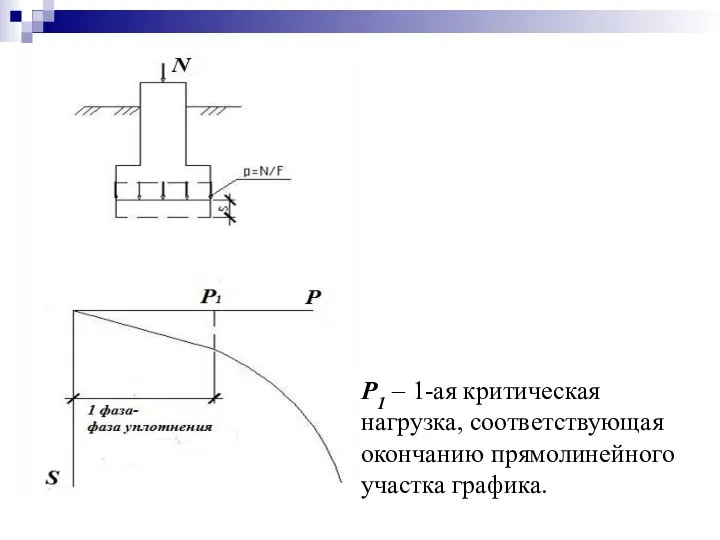
- 13. P1 – 1-ая критическая нагрузка, соответствующая окончанию прямолинейного участка графика.
- 14. Предполагаем, что между осадками и нагрузкой (давлением) существует линейная связь, т. е. p ≤ P1. Основываясь
- 15. Рис. Зависимость осадок от величины давления О давление Р, кН/м2 S, мм Ркр1 Ркр2 ∙ ∙
- 16. Задача Буссинеска - первая задача определения напряжения от действия сосредоточенной силы на линейно-деформируемое полупространство. Модель, предложенная
- 17. От действия силы N во всех точках полупространства возникает сложное напряженное состояние. В каждой точке полупространства,
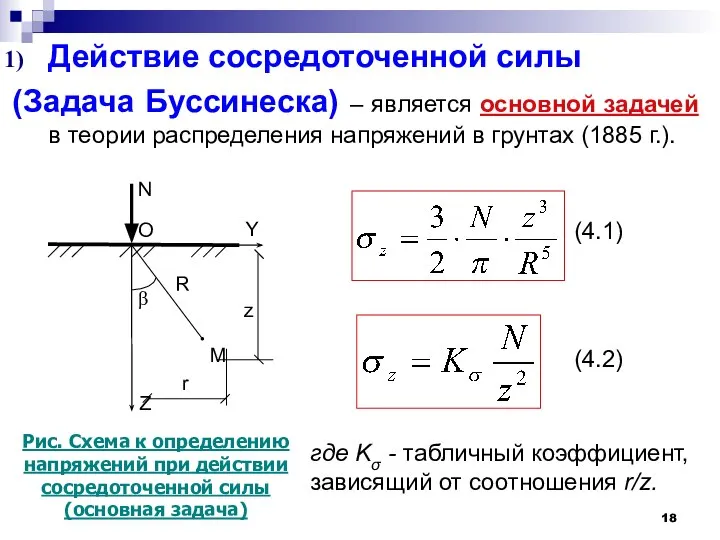
- 18. Действие сосредоточенной силы (Задача Буссинеска) – является основной задачей в теории распределения напряжений в грунтах (1885
- 19. Подставляя это значение в формулу выше, получим: Это общая формула векторного напряжения в любой точке пространства
- 20. Для упрощения вывода принимают как постулат, что напряжение σR пропорционально cos β и обратно пропорционально квадрату
- 21. Под действием силы N точка М переместится в направлении радиуса R на величину S. Чем дальше
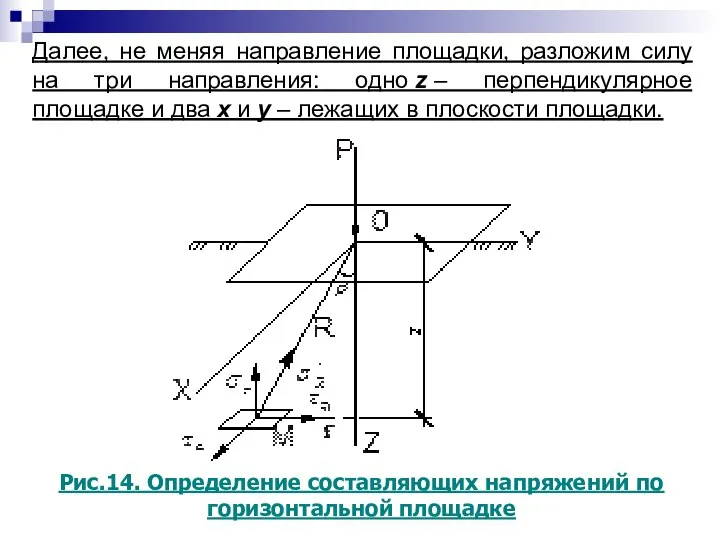
- 22. Далее, не меняя направление площадки, разложим силу на три направления: одно z – перпендикулярное площадке и
- 23. Напряженное состояние в грунтовом массиве в случае плоской задачи может также определяться через главные напряжения (Митчел,
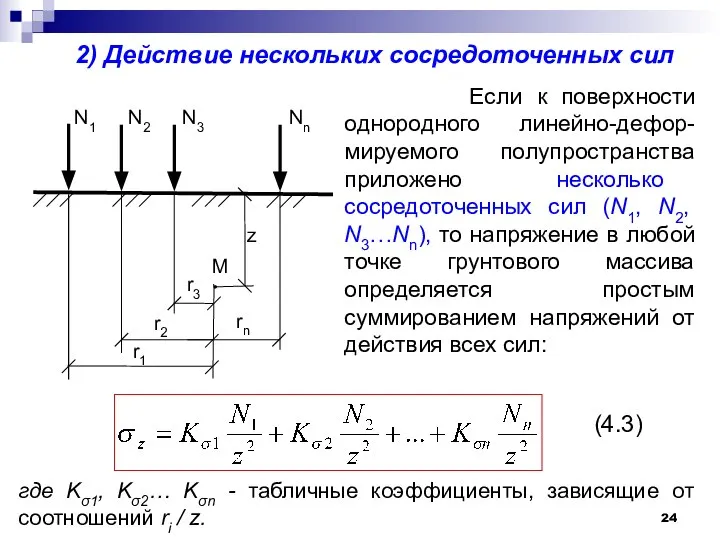
- 24. 2) Действие нескольких сосредоточенных сил Если к поверхности однородного линейно-дефор-мируемого полупространства приложено несколько сосредоточенных сил (N1,
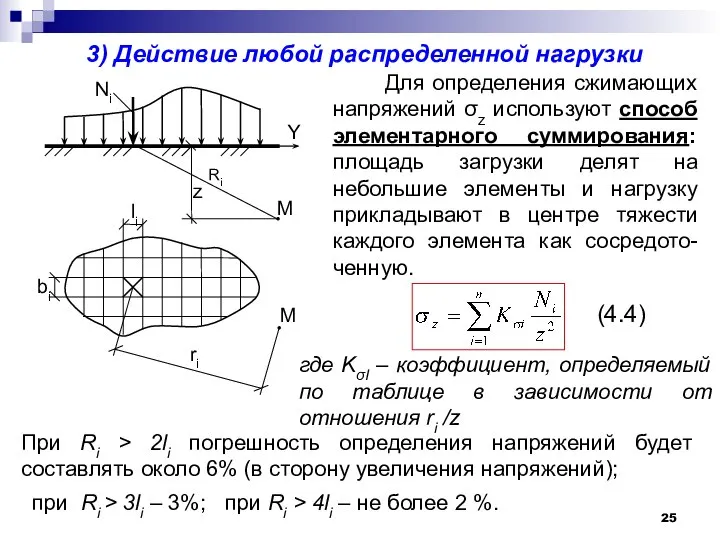
- 25. 3) Действие любой распределенной нагрузки Для определения сжимающих напряжений σz используют способ элементарного суммирования: площадь загрузки
- 26. 4) Действие равномерно распределенной нагрузки по круглым и прямоугольным площадкам z M Y X Впервые решение
- 27. Определение напряжений по методу угловых точек (задача Лява) Для точек, которые не лежат ни на центральной,
- 28. 4.5 Метод угловых точек Сущность метода заключается в том, что грузовая площадь разбивается на такие прямоугольники,
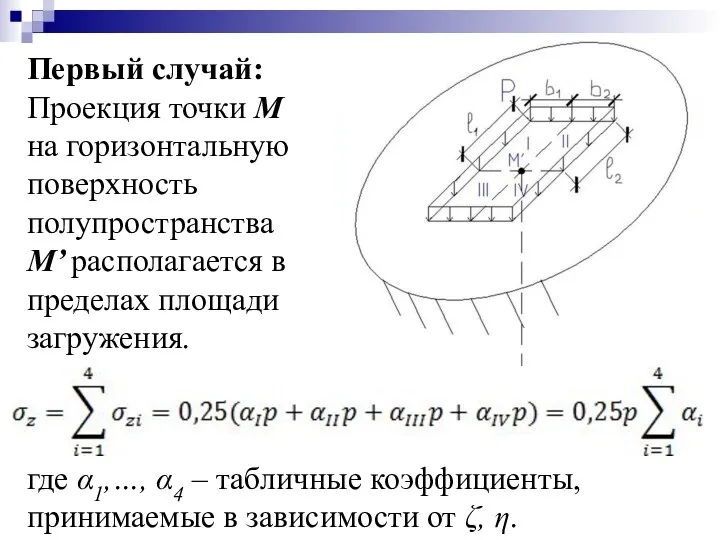
- 29. Первый случай: Проекция точки М на горизонтальную поверхность полупространства М’ располагается в пределах площади загружения. где
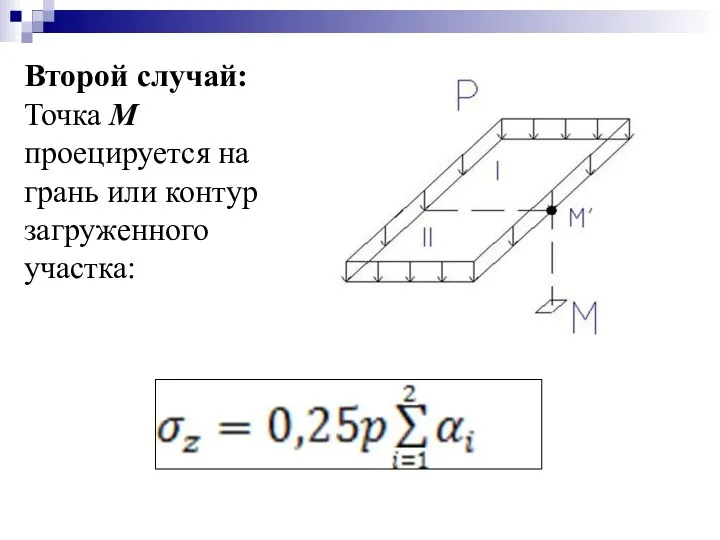
- 30. Второй случай: Точка М проецируется на грань или контур загруженного участка:
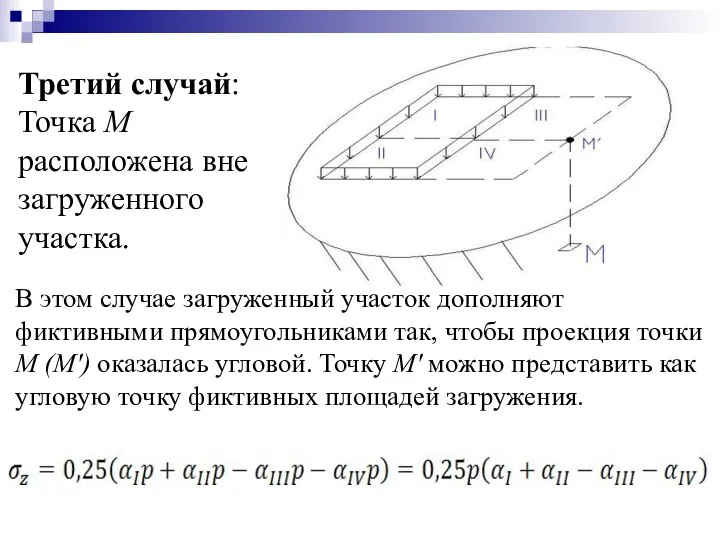
- 31. Третий случай: Точка М расположена вне загруженного участка. В этом случае загруженный участок дополняют фиктивными прямоугольниками
- 32. II Точка М находится внутри прямоугольника: I II M III IV (4.11) III Точка М находится
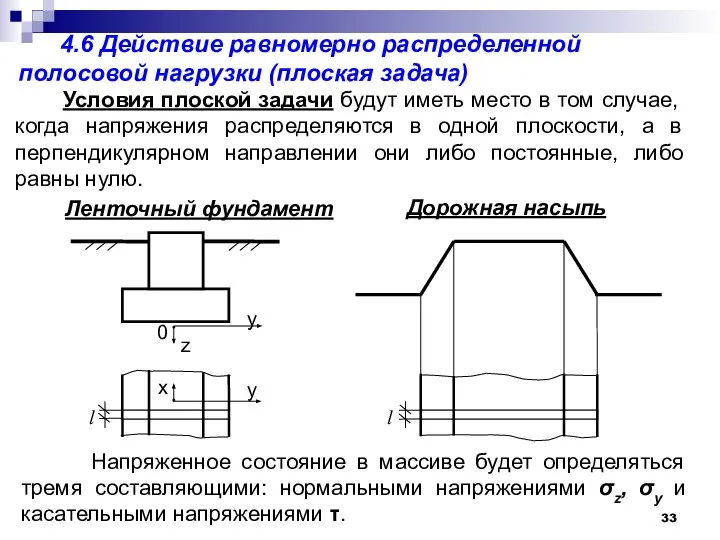
- 33. 4.6 Действие равномерно распределенной полосовой нагрузки (плоская задача) Условия плоской задачи будут иметь место в том
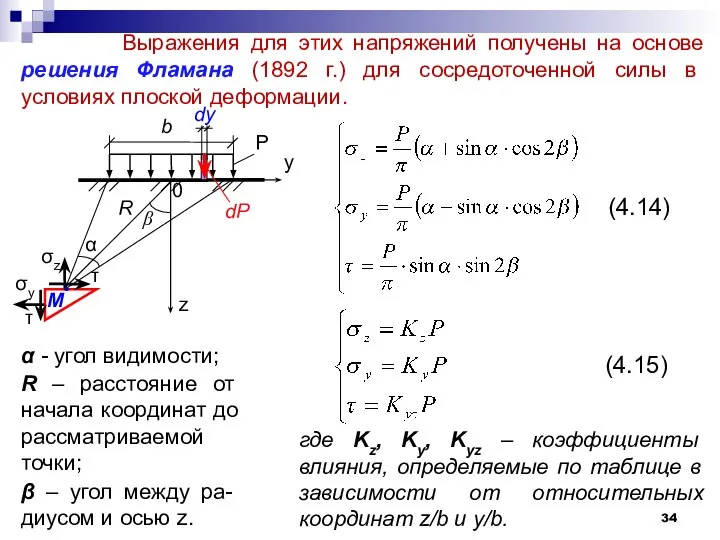
- 34. Выражения для этих напряжений получены на основе решения Фламана (1892 г.) для сосредоточенной силы в условиях
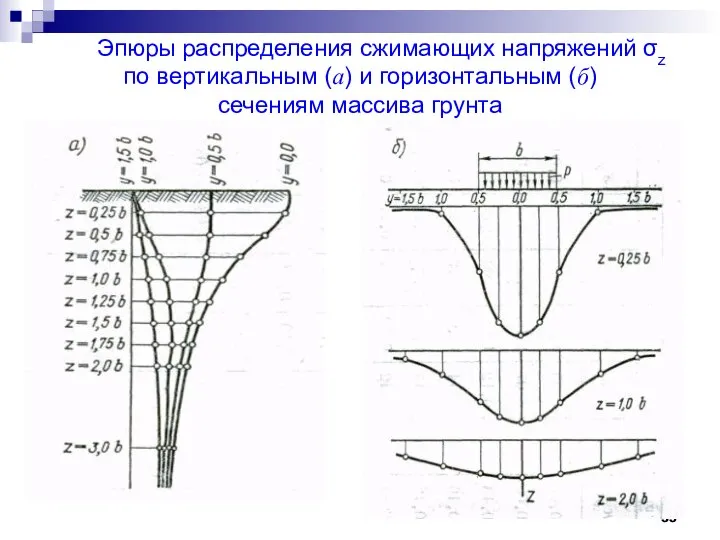
- 35. Эпюры распределения сжимающих напряжений σz по вертикальным (а) и горизонтальным (б) сечениям массива грунта
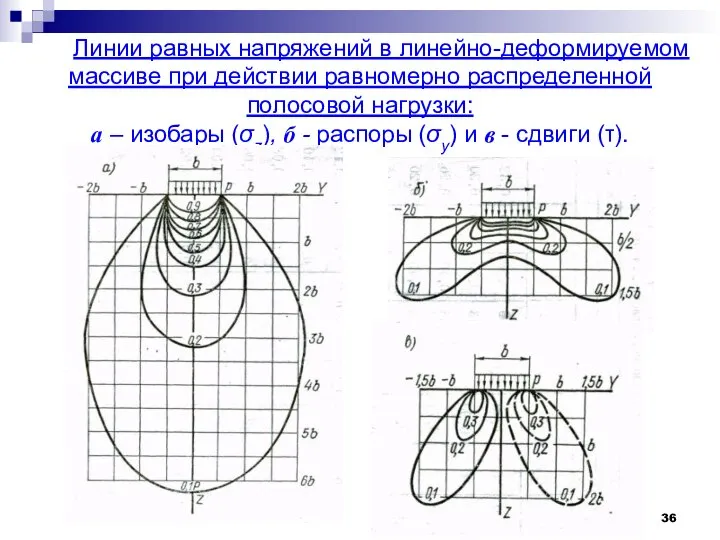
- 36. Линии равных напряжений в линейно-деформируемом массиве при действии равномерно распределенной полосовой нагрузки: а – изобары (σz),
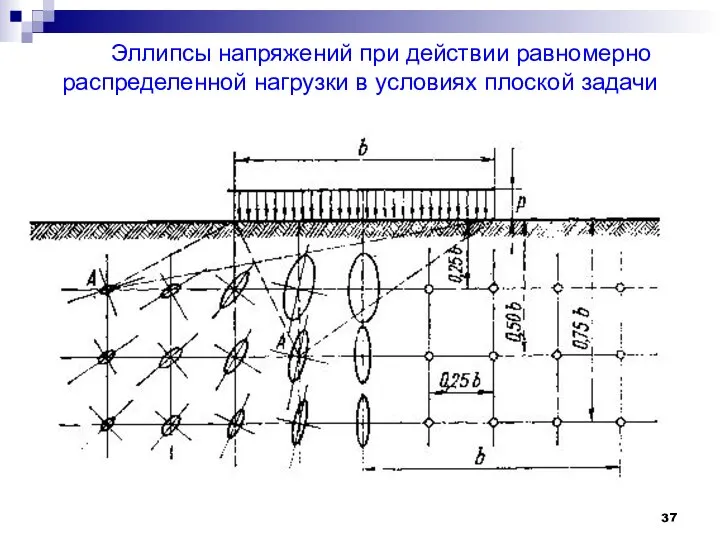
- 37. Эллипсы напряжений при действии равномерно распределенной нагрузки в условиях плоской задачи
- 38. 4.7 Распределение напряжений от действия собственного веса грунта Напряжения от собственного веса грунта увеличиваются с глубиной.
- 40. Скачать презентацию






















 Рациональное строительство с использованием б/у ж/б конструкций
Рациональное строительство с использованием б/у ж/б конструкций Подросток и закон. Интеллектуальная викторина
Подросток и закон. Интеллектуальная викторина Знатоки пословиц - презентация для начальной школы_
Знатоки пословиц - презентация для начальной школы_ Художні напрями та стилі
Художні напрями та стилі Т Е М А: «ОСНОВНЫЕ ПОЛОЖЕНИЯ О ЮРИДИЧЕСКИХ ЛИЦАХ»
Т Е М А: «ОСНОВНЫЕ ПОЛОЖЕНИЯ О ЮРИДИЧЕСКИХ ЛИЦАХ» Приметы на Ивана Купала
Приметы на Ивана Купала Звук. Ультразвук.
Звук. Ультразвук. Режим дня
Режим дня Der Hochschulwesen in Deutschland
Der Hochschulwesen in Deutschland Презентация Функциональная логистика
Презентация Функциональная логистика Презентация на тему "Информационные технологии в деятельности учителя-предметника" - скачать презентации по Педагогике
Презентация на тему "Информационные технологии в деятельности учителя-предметника" - скачать презентации по Педагогике Сторінка Штельмаха Володимипа Миколайовича смт Казанка 2015
Сторінка Штельмаха Володимипа Миколайовича смт Казанка 2015  Острые осложнения сахарного диабета
Острые осложнения сахарного диабета Ключевые задачи на проценты_6 кл_часть 1
Ключевые задачи на проценты_6 кл_часть 1 Социально-экономическая политика современной России
Социально-экономическая политика современной России Хирургическая инфекция . Автор текста д.м.н., профессор БАБАДЖАНОВ Б.Д Узбекистан
Хирургическая инфекция . Автор текста д.м.н., профессор БАБАДЖАНОВ Б.Д Узбекистан Прерыв Itanium
Прерыв Itanium  Домашняя утварь в крестьянском доме
Домашняя утварь в крестьянском доме Pääte - N
Pääte - N Программирование линейных алгоритмов
Программирование линейных алгоритмов Цветная металлургия
Цветная металлургия Современные проблемы архитектуры и градостроительства
Современные проблемы архитектуры и градостроительства Религия древних германцев
Религия древних германцев Қазіргі заман мәдениеті
Қазіргі заман мәдениеті Признаки и организационно правовые формы юридических лиц
Признаки и организационно правовые формы юридических лиц Оценочные обязательства, условные обязательства и условные активы
Оценочные обязательства, условные обязательства и условные активы Суицид ПРОФИЛАКТИКА СУИЦИДА СРЕДИ ДЕТЕЙ И ПОДРОСТКОВ
Суицид ПРОФИЛАКТИКА СУИЦИДА СРЕДИ ДЕТЕЙ И ПОДРОСТКОВ Артикуляционная гимнастика
Артикуляционная гимнастика