Содержание
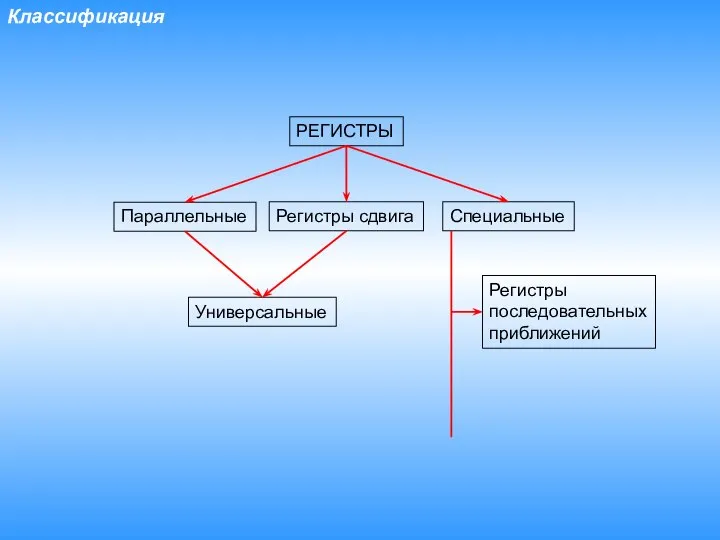
- 2. Классификация РЕГИСТРЫ Параллельные Регистры сдвига Специальные Регистры последовательных приближений Универсальные
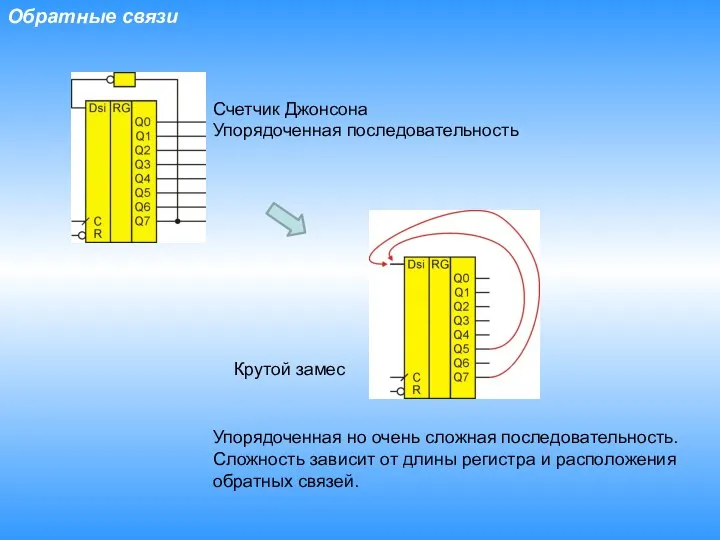
- 3. Обратные связи Счетчик Джонсона Упорядоченная последовательность Упорядоченная но очень сложная последовательность. Сложность зависит от длины регистра
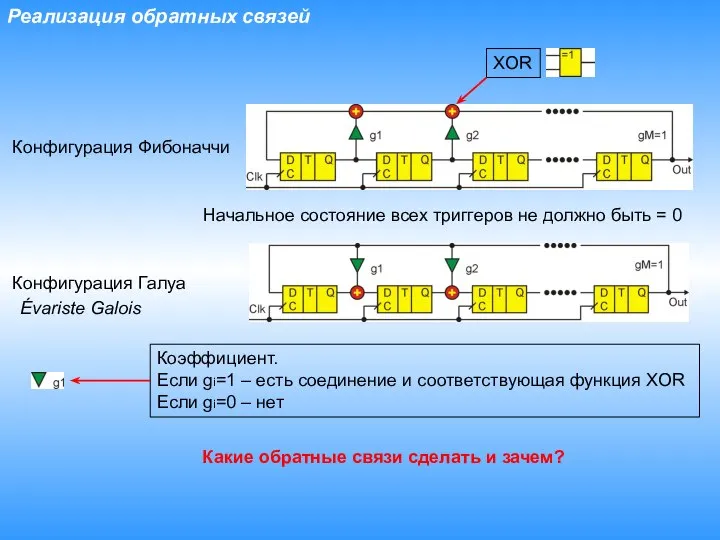
- 4. Реализация обратных связей Конфигурация Фибоначчи Конфигурация Галуа XOR Коэффициент. Если gi=1 – есть соединение и соответствующая
- 5. Последовательности максимальной длины М-последовательности Maximum length sequence Число состояний набора из M триггеров = 2M Для
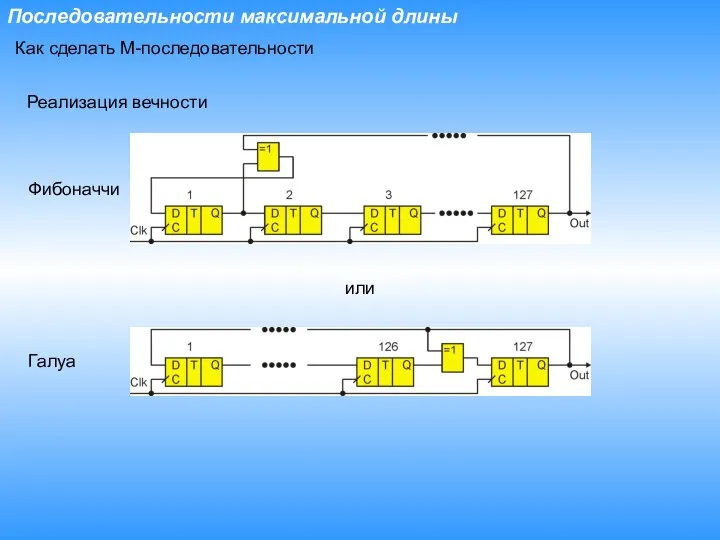
- 6. Последовательности максимальной длины Как сделать М-последовательности Реализация вечности Фибоначчи или Галуа
- 7. Последовательности максимальной длины Как сделать М-последовательности. Кусок таблицы для конфигурации Галуа Переход от номеров отводов Галуа
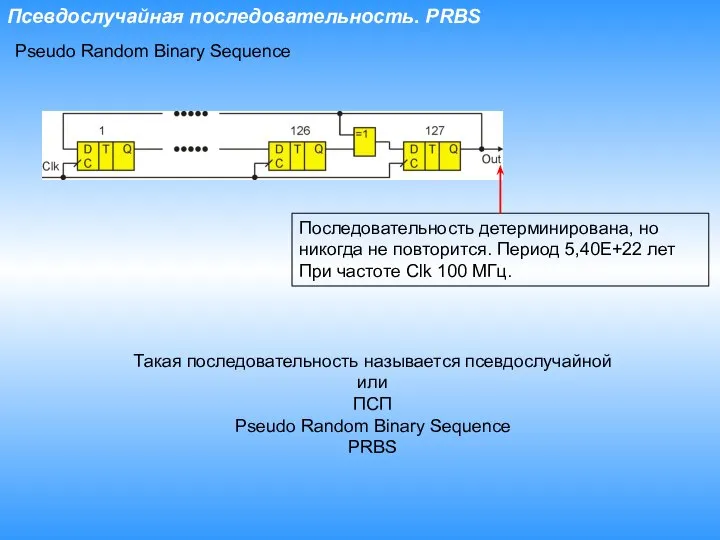
- 8. Псевдослучайная последовательность. PRBS Pseudo Random Binary Sequence Последовательность детерминирована, но никогда не повторится. Период 5,40E+22 лет
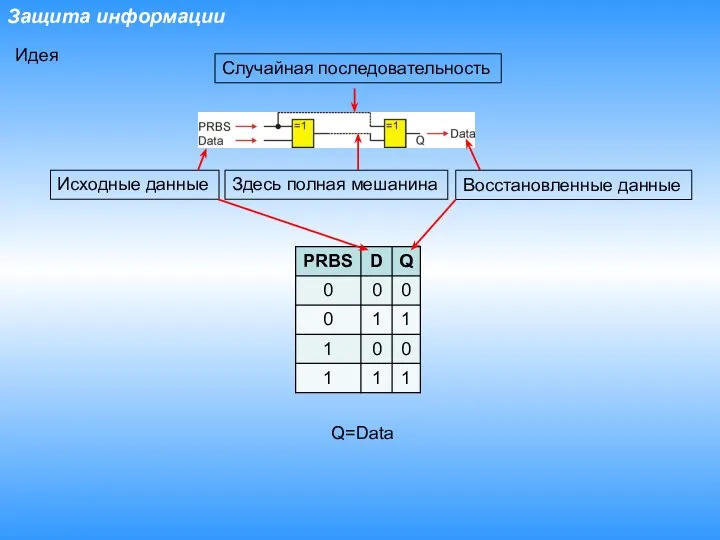
- 9. Защита информации Q=Data Идея Здесь полная мешанина Исходные данные Восстановленные данные Случайная последовательность
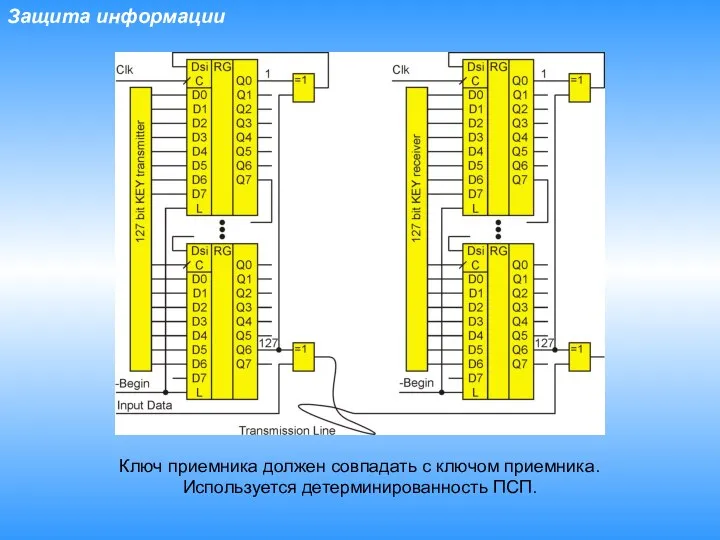
- 10. Защита информации Ключ приемника должен совпадать с ключом приемника. Используется детерминированность ПСП.
- 11. Проверка целостности информации Контрольная сумма или циклический избыточный код Cyclic Redundancy Code (CRC) ИДЕЯ МЕТОДА Допустим
- 12. Проверка целостности информации Двоичная информация Любая информация представляет собой набор 0 и 1. 10010001011110001010100100100101010010001111010 В соответствии
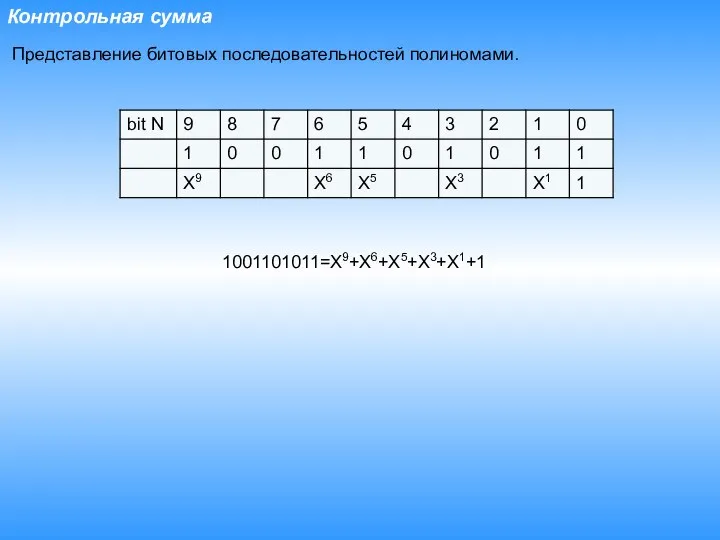
- 13. Контрольная сумма Представление битовых последовательностей полиномами. 1001101011=X9+X6+X5+X3+X1+1
- 14. Контрольная сумма Полиномиальная арифметика. Арифметика по модулю 2 (без переносов). XOR Суммирование = вычитанию A=X9+X6+X5+X3+X1+1 B=X6+X3+X2+1
- 15. Контрольная сумма Полиномиальная арифметика. Арифметика по модулю 2 A=X9+X6+X5+X3+X1+1 B=X6+X3+X2+1 Умножение AxB=(X9+X6+X5+X3+X1+1)x(X6+X3+X2+1)= X15+X12+X11+X9+X7+X6+ X12+X9+X8+X6+X4+X3+ X12+X8+X7+X5+X3+X2+ X9+X6+X5+X3+X1+1
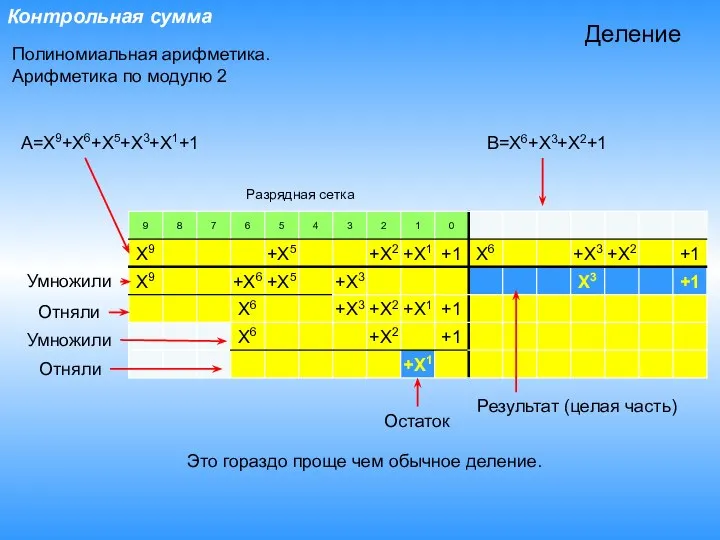
- 16. Контрольная сумма Полиномиальная арифметика. Арифметика по модулю 2 A=X9+X6+X5+X3+X1+1 B=X6+X3+X2+1 Деление Остаток Результат (целая часть) Это
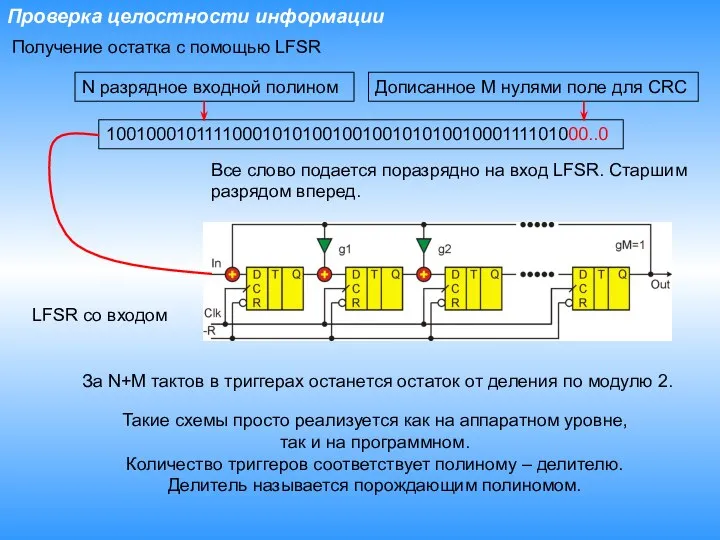
- 17. Проверка целостности информации Получение остатка с помощью LFSR Такие схемы просто реализуется как на аппаратном уровне,
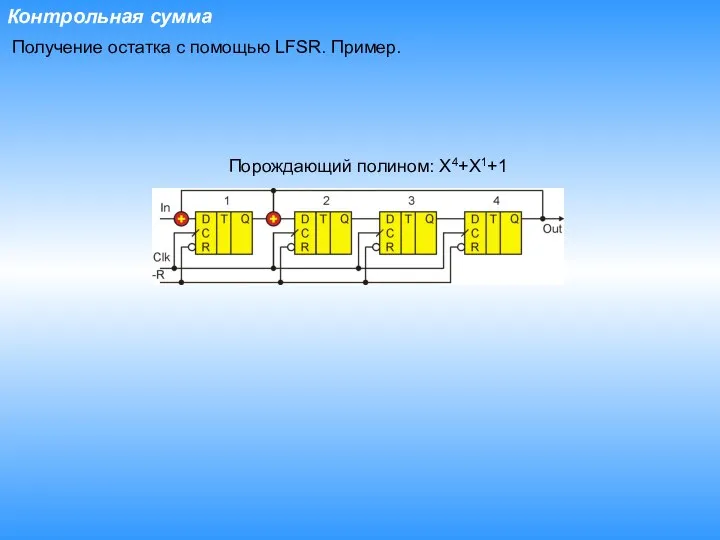
- 18. Контрольная сумма Порождающий полином: X4+X1+1 Получение остатка с помощью LFSR. Пример.
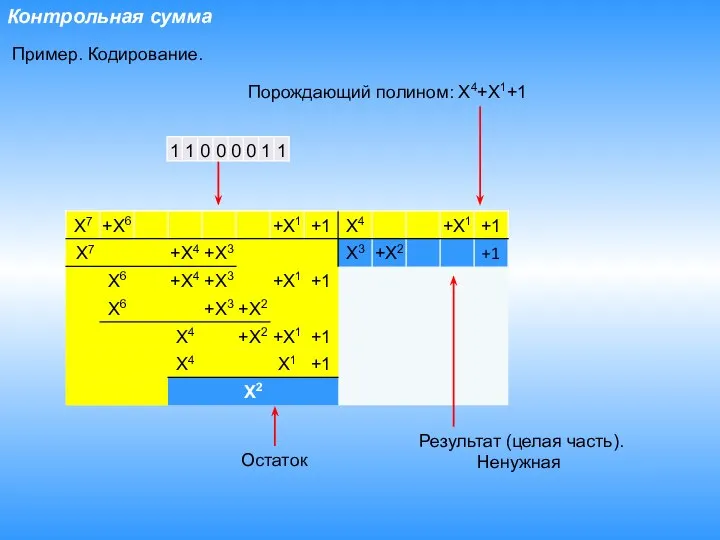
- 19. Контрольная сумма Пример. Кодирование. Порождающий полином: X4+X1+1 Остаток Результат (целая часть). Ненужная
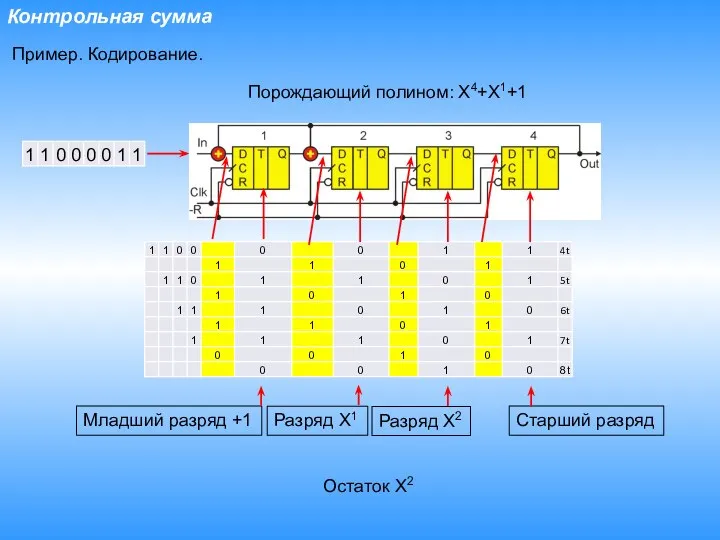
- 20. Контрольная сумма Пример. Кодирование. Остаток X2 Порождающий полином: X4+X1+1 Старший разряд Младший разряд +1 Разряд X1
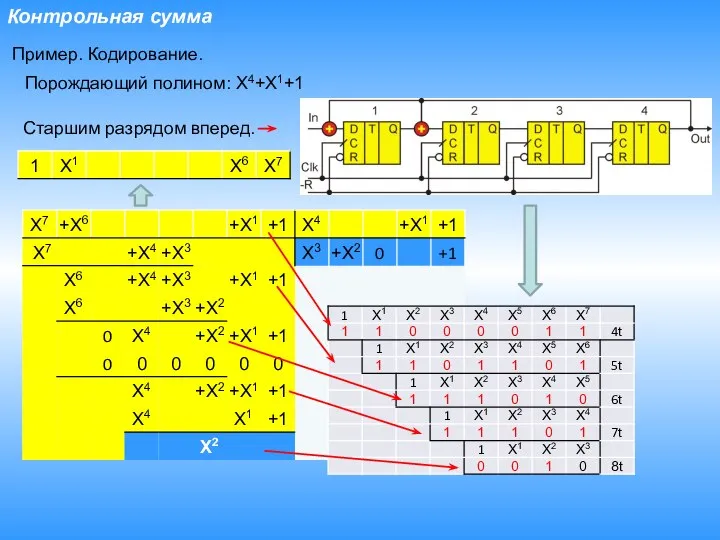
- 21. Контрольная сумма Пример. Кодирование. Порождающий полином: X4+X1+1 Старшим разрядом вперед.
- 22. CRC Cyclic Redundancy Code
- 23. Контрольная сумма
- 25. Скачать презентацию








 Презентацию подготовили: Маргарита Губанова
Презентацию подготовили: Маргарита Губанова Управление процессом обучения на промышленном предприятии На материале ОАО «Каустик» Докладчик – начальник учебного центра ОА
Управление процессом обучения на промышленном предприятии На материале ОАО «Каустик» Докладчик – начальник учебного центра ОА БЖД Лекция (Пораж. Факт.)
БЖД Лекция (Пораж. Факт.) Турниры по мини-футболу среди ветеранов
Турниры по мини-футболу среди ветеранов Стили речи в русском языке
Стили речи в русском языке Взаимосвязь между Р-Т, Т-Х и P-Х проекциями
Взаимосвязь между Р-Т, Т-Х и P-Х проекциями Указание на чертежах предельных отклонений формы и расположение поверхностей
Указание на чертежах предельных отклонений формы и расположение поверхностей Подготовлено Центром Активации Человека «СОТВОРЕНИЕ» 2011г. - презентация
Подготовлено Центром Активации Человека «СОТВОРЕНИЕ» 2011г. - презентация Знаменитые актёры на подмостках ростовской сцены
Знаменитые актёры на подмостках ростовской сцены Обмен нуклеопротеинов
Обмен нуклеопротеинов Храмы России
Храмы России Использование ИКТ на уроках и во внеурочной деятельности Заместитель директора по УВР Затолокина М.В.
Использование ИКТ на уроках и во внеурочной деятельности Заместитель директора по УВР Затолокина М.В. Урок литературного чтения во 2 классе
Урок литературного чтения во 2 классе Разработка часов-колонки
Разработка часов-колонки Русский театр романтизма XIX века Автор учитель МХК Страхова Нина Павлиновна
Русский театр романтизма XIX века Автор учитель МХК Страхова Нина Павлиновна Автомобильные средства заправки и транспортирования горючего и масел
Автомобильные средства заправки и транспортирования горючего и масел Анализ процесса становления и развития института рецидива
Анализ процесса становления и развития института рецидива Тема1. Организация и законодательная основа таможенного дела в РФ.
Тема1. Организация и законодательная основа таможенного дела в РФ. Основы палеонтологии
Основы палеонтологии  Акценты осеннего ухода за кожей лица
Акценты осеннего ухода за кожей лица  Геополитика США в конце ХХ - начале ХХI века
Геополитика США в конце ХХ - начале ХХI века Презентация ШКОЛА ЧЕЛОВЕЧЕСКИХ ОТНОШЕНИЙ
Презентация ШКОЛА ЧЕЛОВЕЧЕСКИХ ОТНОШЕНИЙ Законность и правопорядок
Законность и правопорядок Тоталитаризм. Харизматикалық басшы
Тоталитаризм. Харизматикалық басшы сущность менеджмента
сущность менеджмента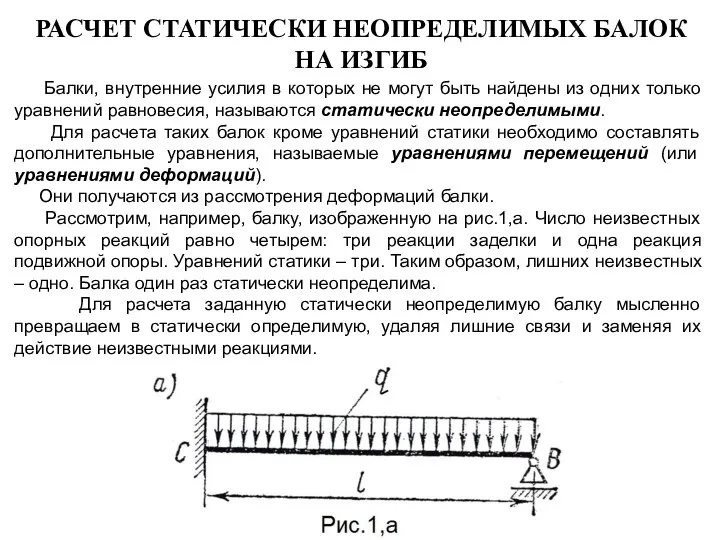 Расчет статически неопределимых балок на изгиб
Расчет статически неопределимых балок на изгиб Правовое государство и гражданское общество
Правовое государство и гражданское общество Работа с родителями. Программа «Спортивное ориентирование»
Работа с родителями. Программа «Спортивное ориентирование»