Содержание
- 2. Рекурсия и ее реализация Рекурсия реализуется на основе подпрограммы, вызывающей саму себя. Первый вызов рекурсивной подпрограммы
- 3. Этапы разработки рекурсивного алгоритма решения задачи 1) параметризация задачи, т.е. выявление различных элементов, от которых зависит
- 4. Рекурсивный алгоритм вычисления факториала Формула факториала: n! =n*(n – 1)*(n – 2)*...*1 управляющий параметр -текущее значение
- 5. Рекурсивная программа вычисления факториала #include "stdafx.h" #include long int fact(int i) { if (i==0) return 1;
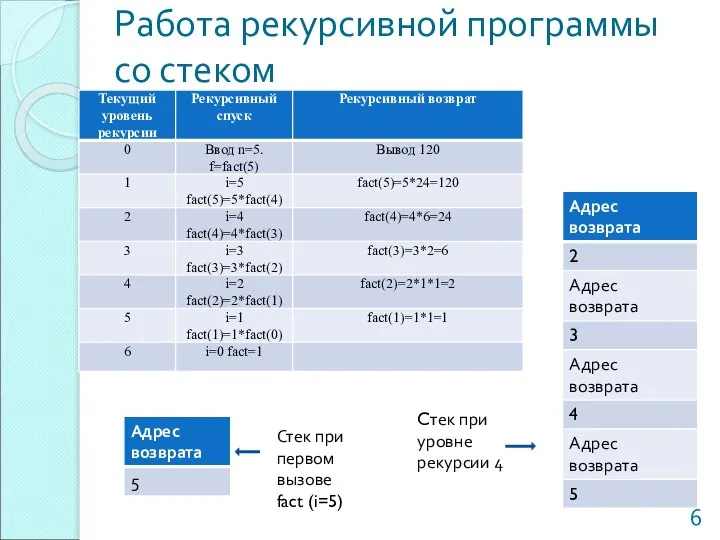
- 6. Работа рекурсивной программы со стеком Стек при первом вызове fact (i=5) Cтек при уровне рекурсии 4
- 7. Роль стека при вызове подпрограммы В из А 1. В вершину стека помещается фрагмент нужного размера.
- 8. Рекурсивное вычисление чисел Фибоначчи F(1)=1,F(2)=1,для любого n>2 F(n)=F(n-1)+F(n-2) #include "stdafx.h" #include long int fib(long int i)
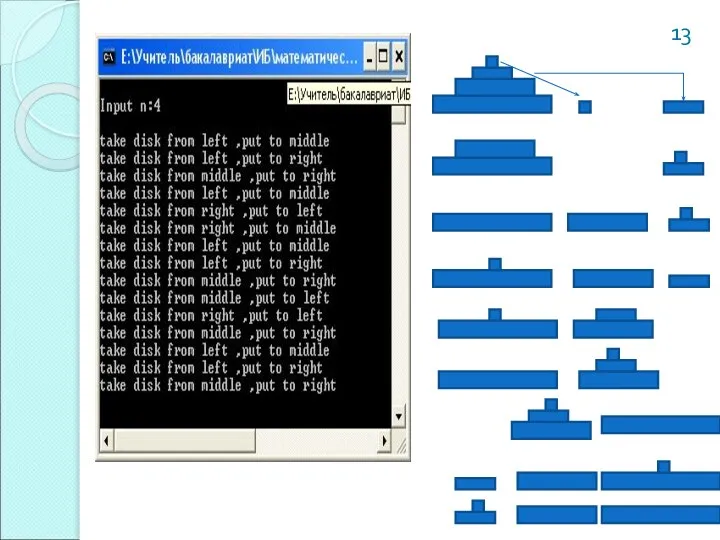
- 9. Задача «Ханойские башни» Существует легенда: «В храме Бендареса находится бронзовая плита с тремя алмазными стержнями. На
- 10. Алгоритм решения задачи «Ханойские башни» Назовем стержни левым (left), средним (middle) и правым (right). Задача состоит
- 11. Программа «Ханойские башни»: обозначения Обозначим тот стержень, с которого следует снять диски, через s1, на который
- 12. #include "stdafx.h" #include enum st {left,middle,right}; void name(st ster) { switch (ster){ case 0: printf(" left
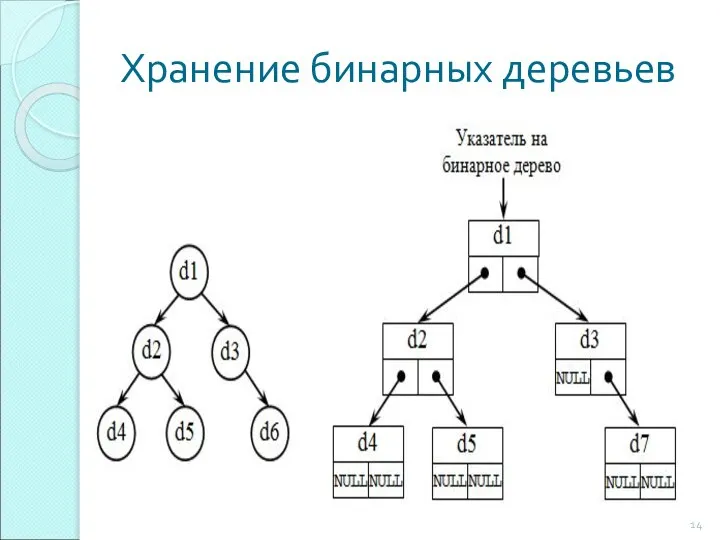
- 14. Хранение бинарных деревьев
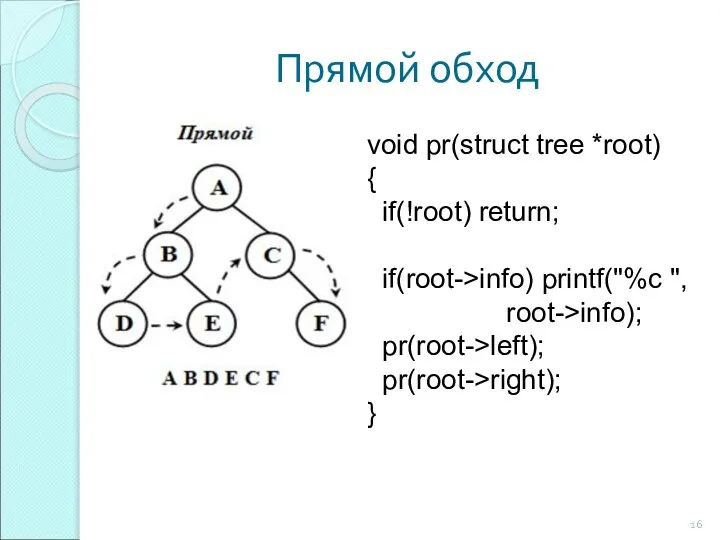
- 15. Обходы бинарных деревьев Прямой (корень – левое поддерево - правое поддерево); обратный (левое поддерево – правое
- 16. Прямой обход void pr(struct tree *root) { if(!root) return; if(root->info) printf("%c ", root->info); pr(root->left); pr(root->right); }
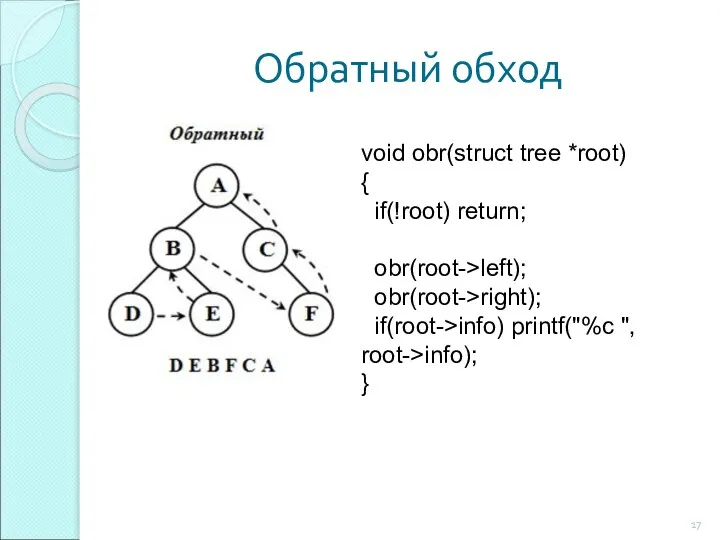
- 17. Обратный обход void obr(struct tree *root) { if(!root) return; obr(root->left); obr(root->right); if(root->info) printf("%c ", root->info); }
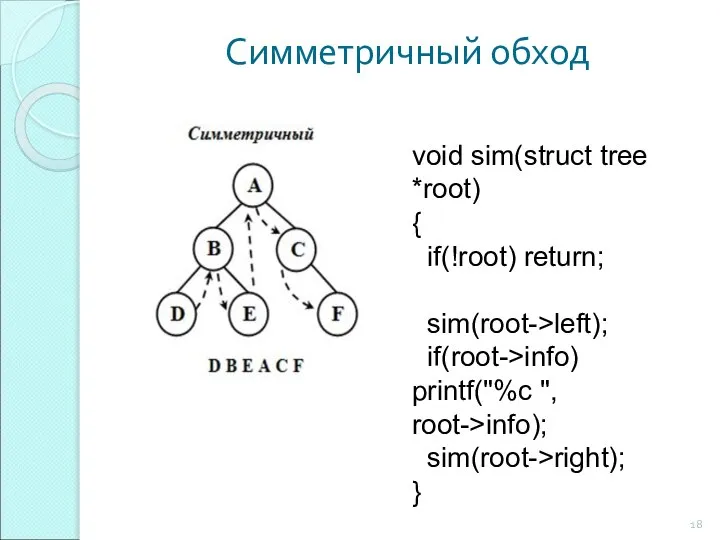
- 18. Симметричный обход void sim(struct tree *root) { if(!root) return; sim(root->left); if(root->info) printf("%c ", root->info); sim(root->right); }
- 19. Переборные задачи. #include "stdafx.h" #include int a[20]; int k; void write_number() { printf("\n"); for (int j=0;j
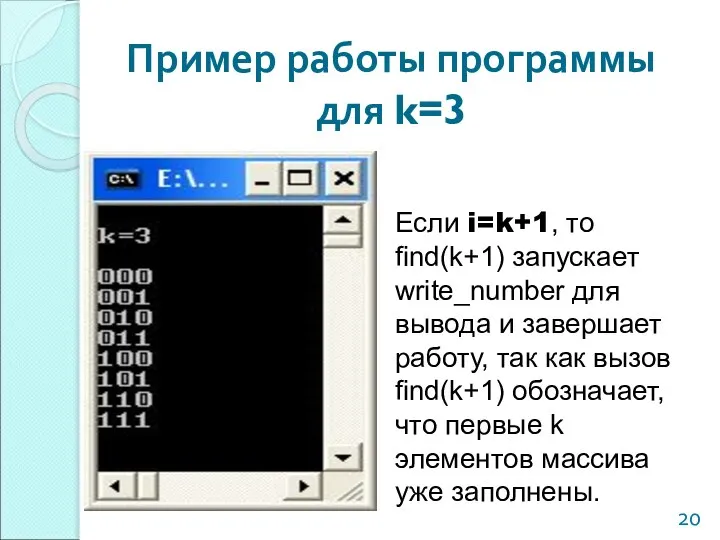
- 20. Пример работы программы для k=3 Если i=k+1, то find(k+1) запускает write_number для вывода и завершает работу,
- 21. Задача о расстановке n ферзей for i1 := 1 to n do begin ферзь[1] := i1;
- 22. Отсечения при переборе for i1 := 1 to n do begin ферзь[1] := i1; for i2
- 23. Простые примеры задач на динамическое программирование Var D : Array [1..50] of LongInt; Function F(X :
- 24. Жадные алгоритмы Жадный алгоритм (greedy algorithm) – это метод решения оптимизационных задач, основанный на том, что
- 25. Дискретная и непрерывная задача о рюкзаке Постановка дискретной задачи. В рюкзак загружаются предметы n различных типов
- 26. Непрерывная задача о рюкзаке Жадный алгоритм: Вычислим цены всех предметов - стоимость предмета разделим на массу
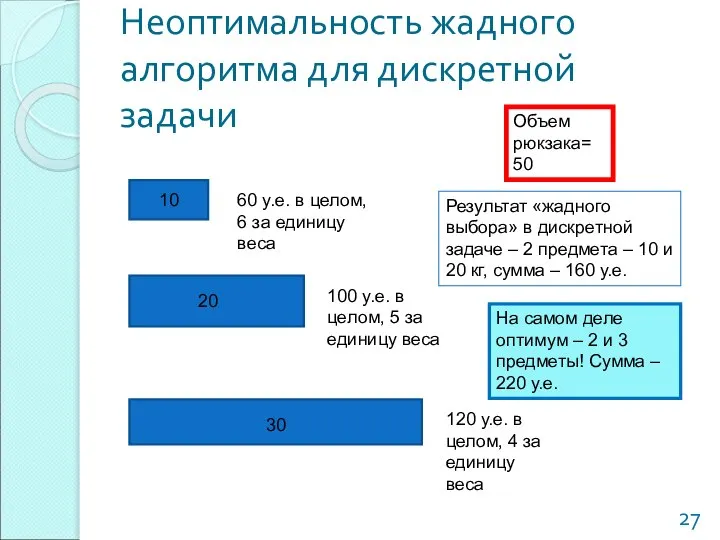
- 27. Неоптимальность жадного алгоритма для дискретной задачи 10 20 30 60 y.е. в целом, 6 за единицу
- 28. Размер задачи, временная сложность Алгоритмическая временная сложность — это зависимость времени исполнения алгоритма от длины или
- 29. Оценка временной сложности операторов программы Tif = Tv+max(Tthen+1,Telse). 1 операция по ветке Then соответствует операции безусловного
- 30. Класс и порядок сложности Определение. Множество вычислительных проблем, для которых существуют алгоритмы, схожие по сложности, называется
- 31. Порядок сложности нерекурсивных и рекурсивных функций s=0; for i:=1 to n do for j:=1 to m
- 32. Грубая оценка временной сложности рекурсивной программы Если верны соотношения T(1)=d; T(n)=a*T(n/c)+b*n, то в зависимости от констант
- 33. Классы сложности алгоритмов О(1) - количество шагов алгоритма не зависит от количества входных данных. Обычно это
- 34. Временная сложность рекурсивного алгоритма для задачи «Ханойские башни» Решение задачи для n дисков сводится к решению
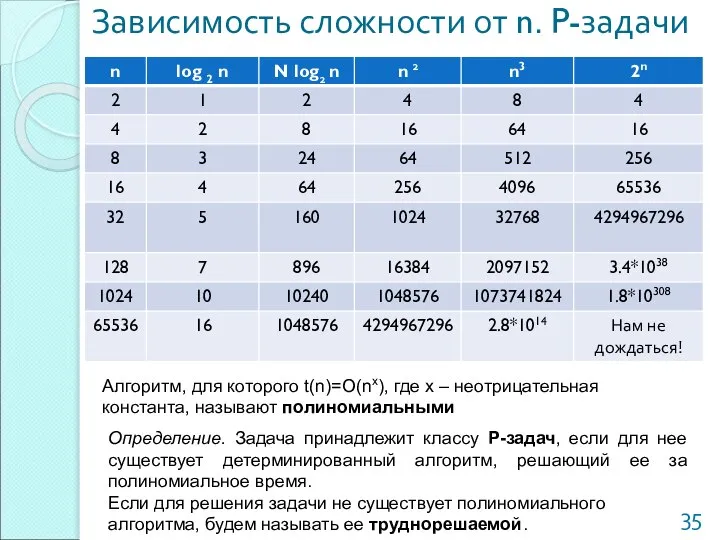
- 35. Зависимость сложности от n. P-задачи Алгоритм, для которого t(n)=O(nx), где x – неотрицательная константа, называют полиномиальными
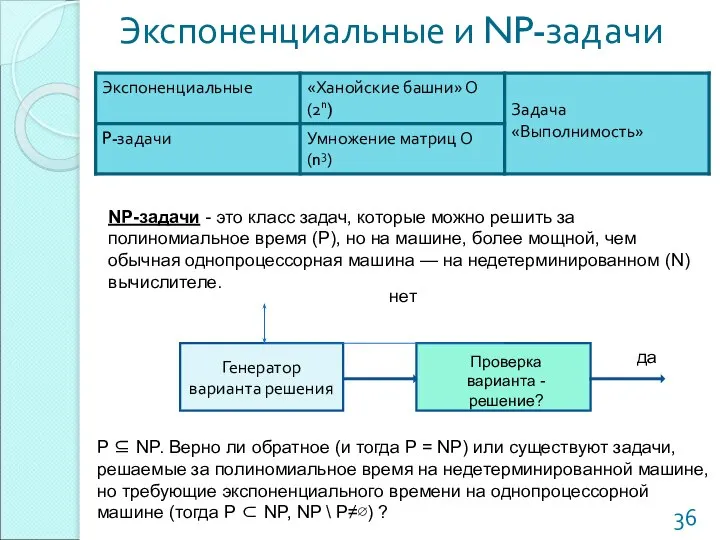
- 36. Экспоненциальные и NP-задачи NP-задачи - это класс задач, которые можно решить за полиномиальное время (Р), но
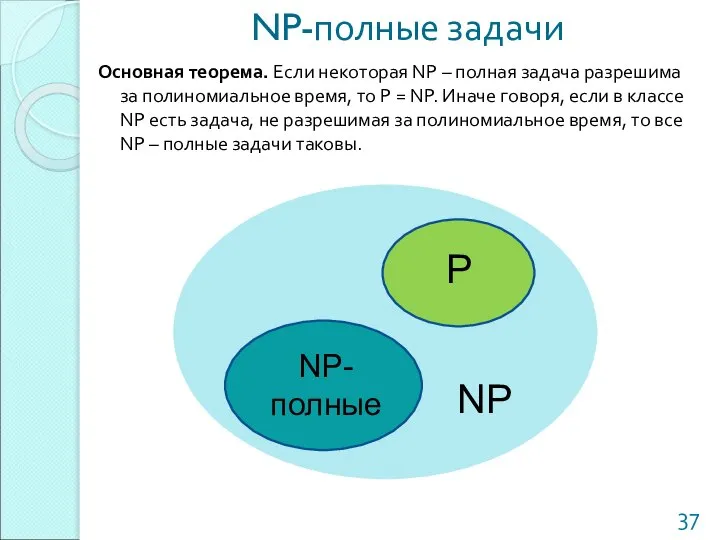
- 37. NP-полные задачи Основная теорема. Если некоторая NP – полная задача разрешима за полиномиальное время, то Р
- 39. Скачать презентацию











![Переборные задачи. #include "stdafx.h" #include int a[20]; int k; void write_number()](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1290950/slide-18.jpg)


![Простые примеры задач на динамическое программирование Var D : Array [1..50]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1290950/slide-22.jpg)










 Иррациональные уравнения и неравенства - презентация по Алгебре
Иррациональные уравнения и неравенства - презентация по Алгебре Лекции по дисциплине «Информационные системы предприятий» Подготовил доцент В.Н. Египко
Лекции по дисциплине «Информационные системы предприятий» Подготовил доцент В.Н. Египко Дене тәрбиесінің қағидалары
Дене тәрбиесінің қағидалары Шаблон по литературе
Шаблон по литературе Презентация на тему "Формы и методы работы с родителями в школе" - скачать презентации по Педагогике
Презентация на тему "Формы и методы работы с родителями в школе" - скачать презентации по Педагогике Билік құрылмындағы партиялар ролі
Билік құрылмындағы партиялар ролі Урок математики по теме: «Четные и нечетные числа»
Урок математики по теме: «Четные и нечетные числа»  tragedia_Beslana
tragedia_Beslana Имидж врача
Имидж врача Презентация "Константин Аркадьевич Райкин" - скачать презентации по МХК
Презентация "Константин Аркадьевич Райкин" - скачать презентации по МХК Основы телекоммуникаций. Устройства передачи сообщений. (Тема 1.10)
Основы телекоммуникаций. Устройства передачи сообщений. (Тема 1.10) Разработка параллельных программ для GPU. Обзор CUDA API
Разработка параллельных программ для GPU. Обзор CUDA API Обследование строительных конструкций зданий и сооружений
Обследование строительных конструкций зданий и сооружений Мастер-класс по окрашиванию бровей и колористике хны
Мастер-класс по окрашиванию бровей и колористике хны Социалните мрежи. - презентация
Социалните мрежи. - презентация Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей
Взаимное положение прямых, прямой и плоскости, и плоскостей. Параллельность плоскостей ЭП_обращение граждан
ЭП_обращение граждан БЖД
БЖД Задача классификации. Метод деревьев решений
Задача классификации. Метод деревьев решений Презентация ЭКСПЕРТИЗА ШОКОЛАДА
Презентация ЭКСПЕРТИЗА ШОКОЛАДА Переход права собственности на жилое помещение в порядке договора купли продажи
Переход права собственности на жилое помещение в порядке договора купли продажи  Дыхательная недостаточность
Дыхательная недостаточность  Программирование и программные среды
Программирование и программные среды БАТЬКІВСЬКІ ЗБОРИ -ТРЕНІНГ /6кл./ «ДІМ, В ЯКОМУ Я ЖИВУ» Підготувала і провела : Беспальченко М.М. 1
БАТЬКІВСЬКІ ЗБОРИ -ТРЕНІНГ /6кл./ «ДІМ, В ЯКОМУ Я ЖИВУ» Підготувала і провела : Беспальченко М.М. 1 Без названия
Без названия ПДД - презентация для начальной школы
ПДД - презентация для начальной школы Аборты. Факторы внутриутробного развития Экология 8 класс
Аборты. Факторы внутриутробного развития Экология 8 класс Презентация "Виды искусства" - скачать презентации по МХК
Презентация "Виды искусства" - скачать презентации по МХК