Содержание
- 2. Shortest paths and spanning trees in graphs Lyzhin Ivan, 2015
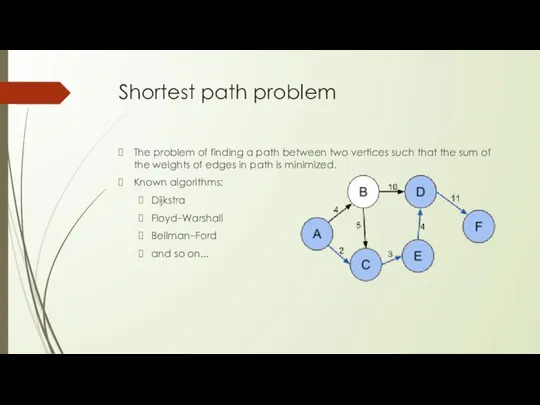
- 3. Shortest path problem The problem of finding a path between two vertices such that the sum
- 4. Dijkstra algorithm There are two sets of vertices – visited and unvisited. For visited vertices we
- 5. Trivial implementation void dijkstra(int s) { vector mark(n, false); vector d(n, INF); d[s] = 0; for
- 6. Implementation with set void dijkstra(int s) { set > q; //(dist[u], u) vector dist(n, INF); dist[s]
- 7. Implementation with priority queue void dijkstra(int s) { priority_queue > q; //(dist[u], u) vector dist(n, INF);
- 8. Floyd–Warshall algorithm Initially, dist[u][u]=0 and for each edge (u, v): dist[u][v]=weight(u, v) On iteration k we
- 9. Implementation void floyd_warshall() { vector > dist(n, vector (n, INF)); for (int i = 0; i
- 10. Bellman–Ford algorithm |V|-1 iterations, on each we try relax distance with all edges. If we can
- 11. Implementation void bellman_ford(int s) { vector dist(n, INF); dist[s] = 0; for (int i = 0;
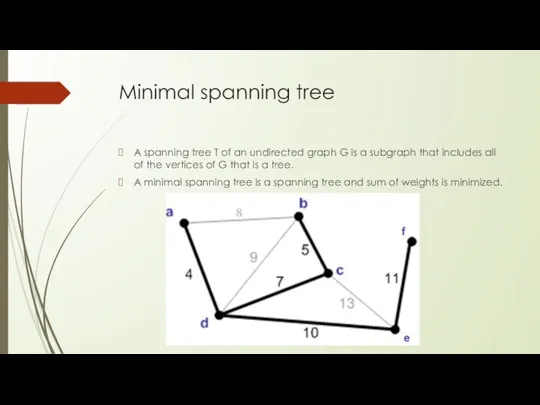
- 12. Minimal spanning tree A spanning tree T of an undirected graph G is a subgraph that
- 13. Prim’s algorithm Initialize a tree with a single vertex, chosen arbitrarily from the graph. Grow the
- 14. Implementation void prima() { set > q; //(dist[u], u) vector dist(n, INF); dist[0] = 0; q.insert(mp(0,
- 15. Kruskal’s algorithm Create a forest F (a set of trees), where each vertex in the graph
- 16. Trivial implementation void trivial_kruskal() { vector color(n); for (int i = 0; i color[i] = i;
- 17. Implementation with DSU void kruskal() { DSU dsu(n); sort(edges.begin(), edges.end()); for(auto e : edges) if(dsu.findSet(e.u)!=dsu.findSet(e.v)) {
- 18. Disjoint-set-union (DSU) Two main operations: Find(U) – return root of set, which contains U, complexity O(1)
- 19. Implementation struct DSU { vector p; DSU(int n) { p.resize(n); for (int i = 0; i
- 20. Path compression When we go up, we can remember root of set for each vertex in
- 21. Union by size int unionSets(int u, int v) { int pu = findSet(u); int pv =
- 22. Links https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm https://en.wikipedia.org/wiki/Floyd–Warshall_algorithm https://en.wikipedia.org/wiki/Bellman–Ford_algorithm https://en.wikipedia.org/wiki/Kruskal%27s_algorithm https://en.wikipedia.org/wiki/Prim%27s_algorithm https://en.wikipedia.org/wiki/Disjoint-set_data_structure http://e-maxx.ru/algo/topological_sort
- 24. Скачать презентацию



![Implementation with set void dijkstra(int s) { set > q; //(dist[u],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1365573/slide-5.jpg)

![Floyd–Warshall algorithm Initially, dist[u][u]=0 and for each edge (u, v): dist[u][v]=weight(u,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1365573/slide-7.jpg)


![Implementation void bellman_ford(int s) { vector dist(n, INF); dist[s] = 0;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1365573/slide-10.jpg)

![Implementation void prima() { set > q; //(dist[u], u) vector dist(n,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1365573/slide-13.jpg)








 ВКР: Правовое регулирование наследования отдельных видов движимого имущества
ВКР: Правовое регулирование наследования отдельных видов движимого имущества Энзимология номенклатура и классификация ферментов Медицинская энзимология (ферменты -3)
Энзимология номенклатура и классификация ферментов Медицинская энзимология (ферменты -3)  Массивы в C#
Массивы в C# Visual Basic
Visual Basic ОГЭ. Немецкий язык
ОГЭ. Немецкий язык Мониторинг метапредметных познавательных компетенций (УУД) Система самообследования в школе
Мониторинг метапредметных познавательных компетенций (УУД) Система самообследования в школе  Международные валютные рынки и риски
Международные валютные рынки и риски  ГЕНЕРАЛЬНОЕ СОГЛАШЕНИЕ ПО ТАРИФАМ И ТОРГОВЛЕ (1947) На начальном этапе – исключительно вопросы торгово-политического регулиров
ГЕНЕРАЛЬНОЕ СОГЛАШЕНИЕ ПО ТАРИФАМ И ТОРГОВЛЕ (1947) На начальном этапе – исключительно вопросы торгово-политического регулиров выполнил: студентка 13 гр. филологич.фак-та Савинова Татьяна проверил: Шереметьева О. А.
выполнил: студентка 13 гр. филологич.фак-та Савинова Татьяна проверил: Шереметьева О. А. Лицензирование деятельности в сфере здравоохранения
Лицензирование деятельности в сфере здравоохранения Стратегии на зрелых и сокращающихся рынках Тема 8
Стратегии на зрелых и сокращающихся рынках Тема 8 Сооружение опор выше обреза фундамента. Тема № 3
Сооружение опор выше обреза фундамента. Тема № 3 Ожоговая болезнь: современные представления и принципы оказания медицинской помощи
Ожоговая болезнь: современные представления и принципы оказания медицинской помощи  Воронежский индустриальный колледж
Воронежский индустриальный колледж Feiertage in Deutschland
Feiertage in Deutschland Верховный суд РФ
Верховный суд РФ Полиомиелит
Полиомиелит Современные методы повышения технических характеристик бетонов
Современные методы повышения технических характеристик бетонов Развитие игрового и опреративного мышления у юных хоккеистов
Развитие игрового и опреративного мышления у юных хоккеистов Хадж и его достоинства
Хадж и его достоинства буква з - презентация для начальной школы
буква з - презентация для начальной школы Как научиться понимать картину
Как научиться понимать картину Денежно - кредитная политика
Денежно - кредитная политика эпоха переворотов
эпоха переворотов Сопряжения. Построение сопряжений
Сопряжения. Построение сопряжений Утренняя гигиеническая гимнастика в туристском походе
Утренняя гигиеническая гимнастика в туристском походе Продукты и технологии компании «КСТ–«М-3»
Продукты и технологии компании «КСТ–«М-3» Что изучает история Древнего мира
Что изучает история Древнего мира