- Главная
- Алгебра
- Теорема о существовании и гладкости обратной функции как частный случай теоремы о неявной функции.

Содержание
- 2. План Функция Область определения функции Неявная функция Теорема о существовании гладкости неявных функций Гладкие функции (Геометрические
- 3. Понятие функции Когда мы наблюдаем какой-нибудь процесс или явление из области экономики, области социальных наук или
- 4. Область определения функции Переменная величина z = f(x, у) называется функцией двух переменных х и у,
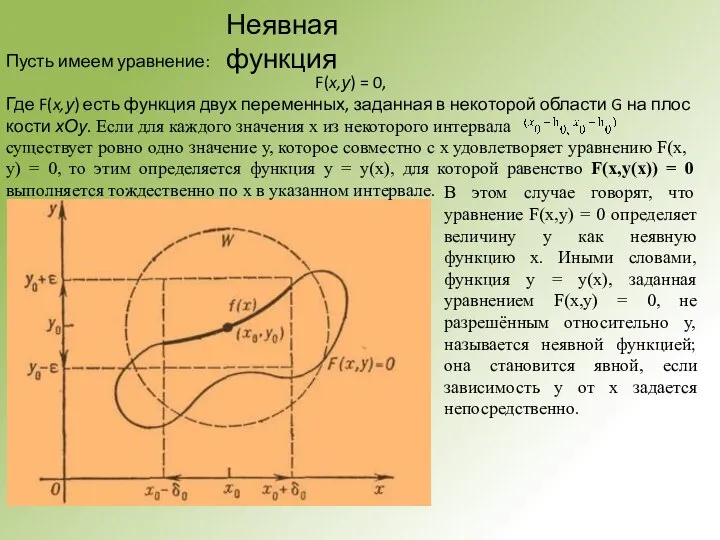
- 5. В этом случае говорят, что уравнение F(x,у) = 0 определяет величину у как неявную функцию х.
- 6. Теорема о существовании и гладкости обратной функции как частный случай теоремы о неявной функции. Теорема. Пусть
- 7. Гладкая функция Гладкая функция или непрерывно дифференцируемая функция- это функция, имеющая непрерывную производную на всем множестве
- 8. Частные производные Определение. Частной производной функции нескольких переменных по одной из этих переменных называется предел от-
- 9. Дифференциал функции Определение. Функция у = f{x) называется дифференцируемой в данной точке х, если приращение ∆y
- 11. Скачать презентацию
План
Функция
Область определения функции
Неявная функция
Теорема о существовании гладкости неявных функций
Гладкие функции
План
Функция
Область определения функции
Неявная функция
Теорема о существовании гладкости неявных функций
Гладкие функции
Частные производные
Дифференциал функции
Экономическая иллюстрация
Понятие функции
Когда мы наблюдаем какой-нибудь процесс или явление из области экономики,
Понятие функции
Когда мы наблюдаем какой-нибудь процесс или явление из области экономики,
Переменная величина при выполнении некоторого комплекса условий может принимать различные значения.
Постоянная величина при выполнении некоторого комплекса условий сохраняет одно и то же значение.
Переменные величины обычно обозначаются последними буквами латинского алфавита (x.,y, z, u, v, w), а постоянные — первыми (а, b, с).
Изучая какое-нибудь явление, мы обычно имеем дело с совокупностью переменных величии, которые связаны между собой так, что каждым значениям одних величин соответствуют значения других. Термин «функция» происходит от латинского слова functio — исполнение, осуществление. Задать функцию — значит задать три объекта: 1) множество X, 2) множество У, 3) правило f.
Определение. Соответствие f, при котором каждому значению х из множества Х соответствует единственное значение у из множества У называется функцией, заданной на множестве Х и принимающей значения из множества У.
Область определения функции
Переменная величина z = f(x, у) называется функцией двух
Область определения функции
Переменная величина z = f(x, у) называется функцией двух
В этом случае говорят, что уравнение F(x,у) = 0 определяет величину
В этом случае говорят, что уравнение F(x,у) = 0 определяет величину
существует ровно одно значение у, которое совместно с х удовлетворяет уравнению F(x,у) = 0, то этим определяется функция у = у(х), для которой равенство F(x,у(х)) = 0 выполняется тождественно по х в указанном интервале.
Неявная функция
Пусть имеем уравнение:
F(x,у) = 0,
Где F(x,у) есть функция двух переменных, заданная в некоторой области G на плоскости хОу. Если для каждого значения х из некоторого интервала
Теорема о существовании и гладкости обратной функции как частный случай теоремы
Теорема о существовании и гладкости обратной функции как частный случай теоремы
Теорема. Пусть функция F(u, x1, x2…) дифференцируема в некоторой окрестности точки Мo (uo, x1o, x2o) пространства R, (R’ обозначаем пространство переменных (х1, х2…) причем частная производная ∂F/∂u непрерывна в точке Mo. Для удобства геометрической иллюстрации будем рассматривать две переменные х1 и х2.
Тогда, если в точке Mo функция F обращается в нуль, а частная производная ∂F/∂u не обращается в нуль, то для любого достаточно малого положительного числа ε найдется такая окрестность точки Mo'(x1o, x2o) пространства R, что в пределах этой окрестности существует единственная функция u = ϕ(x1, х2), которая удовлетворяет условию |u-uo|<ε и является решением уравнения:
F(u, х1, x2)=0, (13)
функция u = ϕ(х1, x2) непрерывна и дифференцируема в указанной окрестности точки Mo’.
Условия, обеспечивающие существование для функции y=f(x) обратной функции.
Гладкая функция
Гладкая функция или непрерывно дифференцируемая функция- это функция, имеющая непрерывную
Гладкая функция
Гладкая функция или непрерывно дифференцируемая функция- это функция, имеющая непрерывную
Теорема. Пусть функция F(u, x1, x2…) дифференцируема в некоторой окрестности точки Мo(uo, x1o, x2o) пространства R, (R’ обозначаем пространство переменных (х1, х2…) причем частная производная ∂F/∂u непрерывна в точке M. Для удобства геометрической иллюстрации будем рассматривать две переменные х1 и х2.
Тогда, если в точке Mo функция F обращается в нуль, а частная производная ∂F/∂u не обращается в нуль, то для любого достаточно малого положительного числа ε найдется такая окрестность точки Mo'(x1o, x2o) пространства R; что в пределах этой окрестности существует единственная функция u = ϕ(х1, x2), которая удовлетворяет условию |u-uo|<ε и является решением уравнения:
F(u, х1, x2)=0, (1)
причем эта функция u = ϕ(х1, x2) непрерывна и дифференцируема в указанной окрестности точки Mo’.
Частные производные
Определение. Частной производной функции нескольких переменных по одной из
Частные производные
Определение. Частной производной функции нескольких переменных по одной из
Дифференциал функции
Определение. Функция у = f{x) называется дифференцируемой в данной точке
Дифференциал функции
Определение. Функция у = f{x) называется дифференцируемой в данной точке
Теорема. Для, того чтобы функция у = f(x) являлась дифференцируемой в данной точке х, необходимо и достаточно, чтобы она имела в этой точке конечную производную.







 Молетроника. Спинтроника
Молетроника. Спинтроника Определение численности персонала предприятия
Определение численности персонала предприятия Формирование критериального подхода оценки СКАЖИ И Я ЗАБУДУ. ПОКАЖИ И Я ЗАПОМНЮ. ВОВЛЕКИ И Я НАУЧУСЬ. КИ
Формирование критериального подхода оценки СКАЖИ И Я ЗАБУДУ. ПОКАЖИ И Я ЗАПОМНЮ. ВОВЛЕКИ И Я НАУЧУСЬ. КИ МОУ «Самаевская СОШ» Презентация по русскому языку к уроку «Правописание безударных гласных в корне» Учитель: Лбова Л. А.
МОУ «Самаевская СОШ» Презентация по русскому языку к уроку «Правописание безударных гласных в корне» Учитель: Лбова Л. А. Презентация на тему Методы селекции растений
Презентация на тему Методы селекции растений  Направления защиты информации в информационных системах
Направления защиты информации в информационных системах Маркетинг персонала
Маркетинг персонала Основы объектно - ориентированного программирования на Delphi
Основы объектно - ориентированного программирования на Delphi Способы адресации в микропроцессорных системах
Способы адресации в микропроцессорных системах Духовная сфера
Духовная сфера Дихотомическая модель Вебера – Вильсона
Дихотомическая модель Вебера – Вильсона  Методы (подпрограммы) в Java-программе (Лекция 7)
Методы (подпрограммы) в Java-программе (Лекция 7) Сканирование карт
Сканирование карт Роль и место контрактов международной торговли в таможенном оформлении товаров Выполнили студентки 3 курса ФТД гру
Роль и место контрактов международной торговли в таможенном оформлении товаров Выполнили студентки 3 курса ФТД гру Презентация "Россия в XVIII в" - скачать презентации по МХК
Презентация "Россия в XVIII в" - скачать презентации по МХК Успех
Успех Анализ проблем обеспечения безопасности соединений в сетях IP-телефонии
Анализ проблем обеспечения безопасности соединений в сетях IP-телефонии Цикл уроков для 9 класса Последовательности (можно ли объять необъятное…) Учитель – Закуцкая М.В. ГОУ лицей 179 2010 – 2011 уч.г. - презентация
Цикл уроков для 9 класса Последовательности (можно ли объять необъятное…) Учитель – Закуцкая М.В. ГОУ лицей 179 2010 – 2011 уч.г. - презентация Національна культура та етапи її формування
Національна культура та етапи її формування Язык программирования Паскаль. (Тема 1)
Язык программирования Паскаль. (Тема 1) Проект педагогической деятельности по направлению семейного воспитания “Воспитание семьянина” ГКОУ РО для детей-сирот и детей, оставшихся без попечения родител
Проект педагогической деятельности по направлению семейного воспитания “Воспитание семьянина” ГКОУ РО для детей-сирот и детей, оставшихся без попечения родител Müssen
Müssen Тренажер по русскому языку 4 класс Автор : Кулакова Наталья Ивановна, учитель начальных классов СШ № 26 г. Гродно, 2013 год
Тренажер по русскому языку 4 класс Автор : Кулакова Наталья Ивановна, учитель начальных классов СШ № 26 г. Гродно, 2013 год Қыс
Қыс Фольклор. Русские народные песни
Фольклор. Русские народные песни Налог на имущество физических лиц
Налог на имущество физических лиц Күштік берілістер, муфталар
Күштік берілістер, муфталар Тема 11. Инвестиционная политика предприятия.
Тема 11. Инвестиционная политика предприятия.