Содержание
- 2. 5. МИНИМУМ ВЫПУКЛОЙ ФУНКЦИИ 5.1. Локальный и глобальный минимум выпуклой функции. 5.2. Минимум дифференцируемой выпуклой функции.
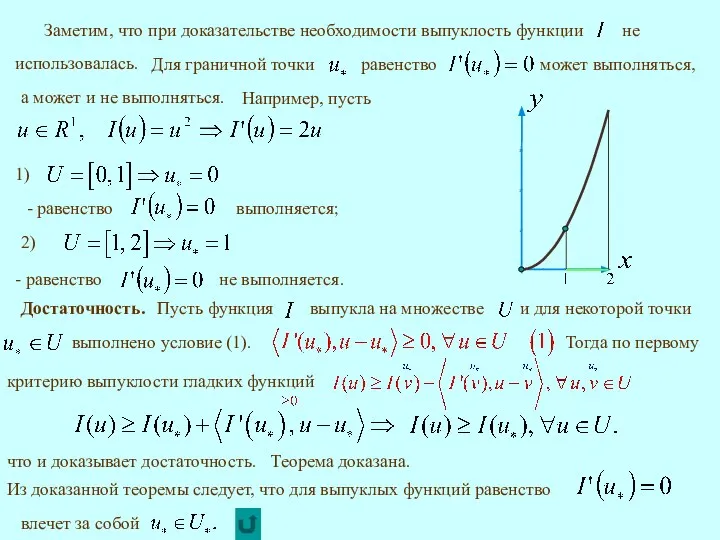
- 3. 5.1. Локальный и глобальный минимум выпуклой функции. Теорема 1. выпукла. одновременно является точкой ее глобального минимума
- 4. С другой стороны, или Таким образом, всякий локальный минимум одновременно является глобальным. Тогда Таким образом,
- 5. то для строго выпуклых функций 5.2. Минимум дифференцируемой выпуклой функции. Теорема 2.
- 6. Доказательство. Необходимость. что Тогда Необходимость доказана.
- 7. а может и не выполняться. Например, пусть Достаточность. что и доказывает достаточность. Теорема доказана.
- 8. 5.3. Минимум выпуклой функции, дифференцируемой по всем возможным направлениям. Требование существования производных по направлениям Это тем
- 9. Доказательство. Необходимость. Тогда Необходимость доказана. Достаточность.
- 10. Полагаем
- 11. имеем то для направления что и требовалось доказать. Тогда Заметим, что
- 12. Тогда является обобщением теоремы 2 Таким образом, теорема 3 Получили формулировку теоремы 2. (функций дифференцируемых по
- 13. Решение. Таким образом, В этих точках функция является дифференцируемой, поэтому
- 14. Тогда одна из производных должна быть строго отрицательной.
- 16. Скачать презентацию












 Пневмонии и гнойные заболевания лёгких. Этиология. Клиника. Диагностика. Осложнения. Основные принципы лечения Доцент Т.Ю.Че
Пневмонии и гнойные заболевания лёгких. Этиология. Клиника. Диагностика. Осложнения. Основные принципы лечения Доцент Т.Ю.Че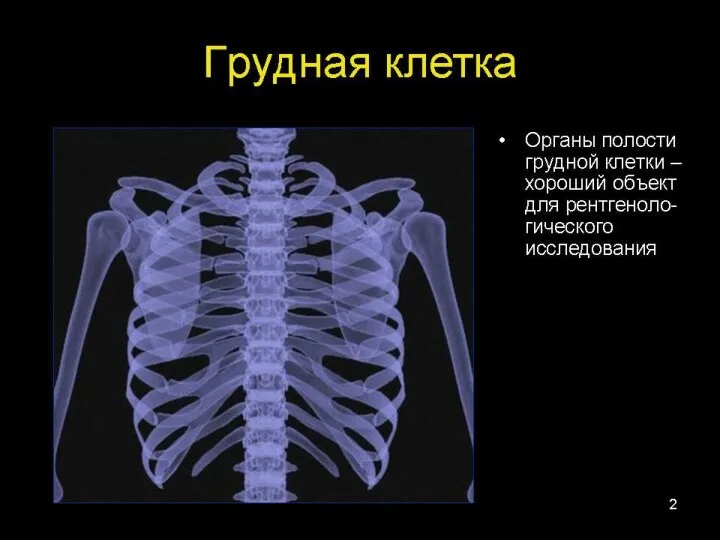 Презентация на тему "Лёгкие в лучевом изображении и лучевые синдромы заболеваний лёгких" - скачать презентации по Медицине
Презентация на тему "Лёгкие в лучевом изображении и лучевые синдромы заболеваний лёгких" - скачать презентации по Медицине Дозирование нагрузки при занятиях бегом. Легкоатлетическая гимнастика
Дозирование нагрузки при занятиях бегом. Легкоатлетическая гимнастика Облік розрахунків з дебіторами
Облік розрахунків з дебіторами Исследовательская работа «Кристаллы. Выращивание кристаллов». Выполнили ученицы 8 класса Печниковской средней школы Каргопольс
Исследовательская работа «Кристаллы. Выращивание кристаллов». Выполнили ученицы 8 класса Печниковской средней школы Каргопольс Процесс управления и управленческие решения
Процесс управления и управленческие решения Объектно-ориентированное проектирование ПС (часть 2)
Объектно-ориентированное проектирование ПС (часть 2) Лингвистические особенности речи политических лидеров (на примере предвыборных речей Барака Обамы и Дональда Трампа)
Лингвистические особенности речи политических лидеров (на примере предвыборных речей Барака Обамы и Дональда Трампа) Гаджеты в жизни ребёнка
Гаджеты в жизни ребёнка Планирование процесса исследования систем управления: основные понятия и организация работы
Планирование процесса исследования систем управления: основные понятия и организация работы Театр моды "Силуэт"
Театр моды "Силуэт" Eвропейский стандарт цифрового эфирного телевидения DVB-T2
Eвропейский стандарт цифрового эфирного телевидения DVB-T2 Реформы Петра І и судьбы российской и украинской художественной культуры
Реформы Петра І и судьбы российской и украинской художественной культуры Поверхности. Способы задания поверхности
Поверхности. Способы задания поверхности Основы аудита
Основы аудита  Шестипульсовая (трехфазная) мостовая схема управляемого выпрямителя
Шестипульсовая (трехфазная) мостовая схема управляемого выпрямителя Презентацию подготовил ученик 8 класса Ерошенко Григорий
Презентацию подготовил ученик 8 класса Ерошенко Григорий Аграрный календарь. Обычаи и обряды. Праздничность. Игра Часть 4
Аграрный календарь. Обычаи и обряды. Праздничность. Игра Часть 4 Общая патология клетки 2
Общая патология клетки 2 Политический конфликт
Политический конфликт Великобритания (Политическая система, образование, культура и традиции)
Великобритания (Политическая система, образование, культура и традиции) Презентация Академические звания
Презентация Академические звания Свойства операций
Свойства операций  Стандарты финансовой отчетности
Стандарты финансовой отчетности  Культура адыгских народов
Культура адыгских народов Творческие работы учащихся 4 класса Учитель Шутова Марина Викторовна
Творческие работы учащихся 4 класса Учитель Шутова Марина Викторовна Relational Algebra
Relational Algebra Маркетинговое исследование предпочтений потребителей печенья «Юбилейное» Юрлова Виктория, ДС.02
Маркетинговое исследование предпочтений потребителей печенья «Юбилейное» Юрлова Виктория, ДС.02