Содержание
- 2. СОДЕРЖАНИЕ 1. Формальная постановка и поиск решения задачи о минимальном разрезе между двумя вершинами на взвешенном
- 3. ЗАДАЧА О МИНИМАЛЬНОМ РАЗРЕЗЕ МЕЖДУ ДВУМЯ ВЕРШИНАМИ НА ВЗВЕШЕННОМ ОРГРАФЕ Часть 1
- 4. ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ О МИНИМАЛЬНОМ РАЗРЕЗЕ МЕЖДУ ВЕРШИНАМИ S И T
- 5. АЛГОРИТМ ПОИСКА РЕШЕНИЯ ЗАДАЧИ О МИНИМАЛЬНОМ РАЗРЕЗЕ МЕЖДУ ДВУМЯ ВЕРШИНАМИ ПЕРЕБОРОМ 1 Шаг. Выбор ранее не
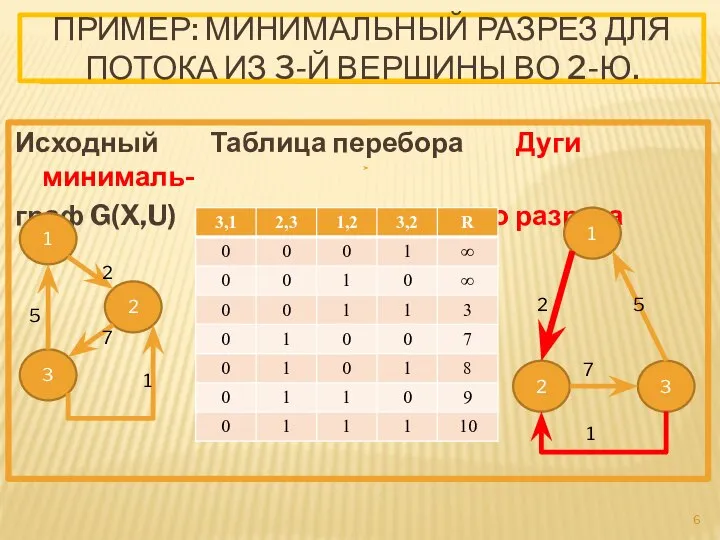
- 6. ПРИМЕР: МИНИМАЛЬНЫЙ РАЗРЕЗ ДЛЯ ПОТОКА ИЗ 3-Й ВЕРШИНЫ ВО 2-Ю. Исходный Таблица перебора Дуги минималь- граф
- 7. РЕШИТЬ ТРИ ЗАДАЧИ САМОСТОЯТЕЛЬНО 1. Определить 2. Определить 3.Определить кратчайший максимальный минимальный путь между поток из
- 8. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 1 - 9
- 9. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 10 - 18
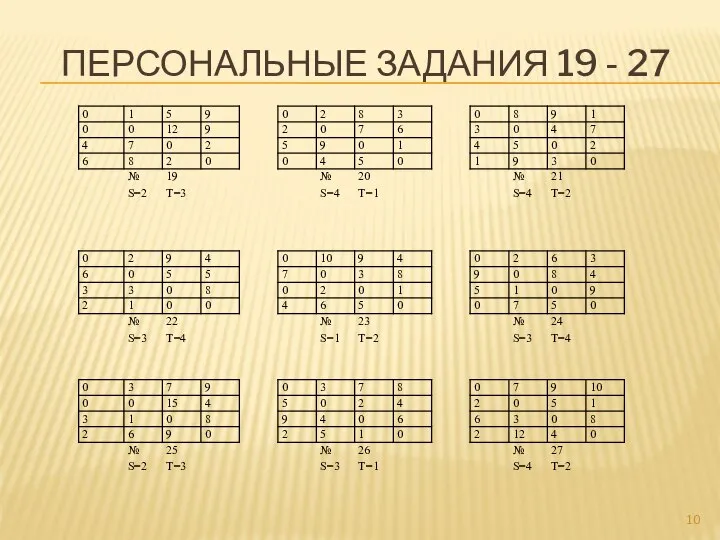
- 10. ПЕРСОНАЛЬНЫЕ ЗАДАНИЯ 19 - 27
- 11. Минимальные разрезы в сильносвязных (бисвязных) орграфах Часть 3.
- 12. К ИСТОРИИ ВОЗНИКНОВЕНИЯ ПРОБЛЕМЫ В середине прошлого века развилась полупроводниковая электроника, разброс параметров которой вызвал резкое
- 13. ЭКОНОМИЧЕСКИЙ ХАРАКТЕР ЗАДАЧИ Отладка блоков электронных схем осуществляется в порядке, позволяющем использовать уже проверенные и исправные
- 14. СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ На взвешенном бисвязном ориентированном графе требуется выделить такое подмножество дуг, для которого справедливо:
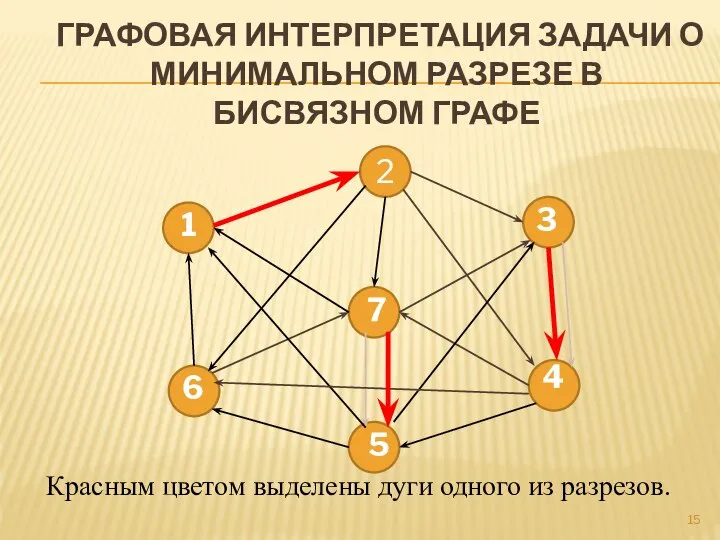
- 15. ГРАФОВАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧИ О МИНИМАЛЬНОМ РАЗРЕЗЕ В БИСВЯЗНОМ ГРАФЕ 2 1 7 4 3 5 6
- 16. ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯ
- 17. ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ О МИНИМАЛЬНОМ РАЗРЕЗЕ В БИСВЯЗНОМ ВЗВЕШЕННОМ ГРАФЕ
- 18. ПРИМЕР 1: ПОСТАНОВКА ЗАДАЧИ 1 3 2 4 9 5 3 7 4 3
- 19. ЖУРНАЛ “IEEE TRANSACTIONS ON CIRCUIT THEORY” 60-е годы: статья Лемпела с Седербаума о новой математике, развитой
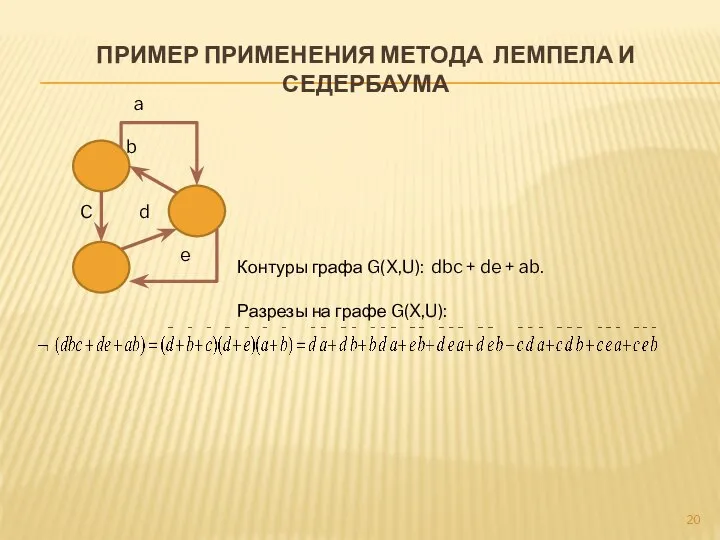
- 20. ПРИМЕР ПРИМЕНЕНИЯ МЕТОДА ЛЕМПЕЛА И СЕДЕРБАУМА a b C d e Контуры графа G(X,U): dbc +
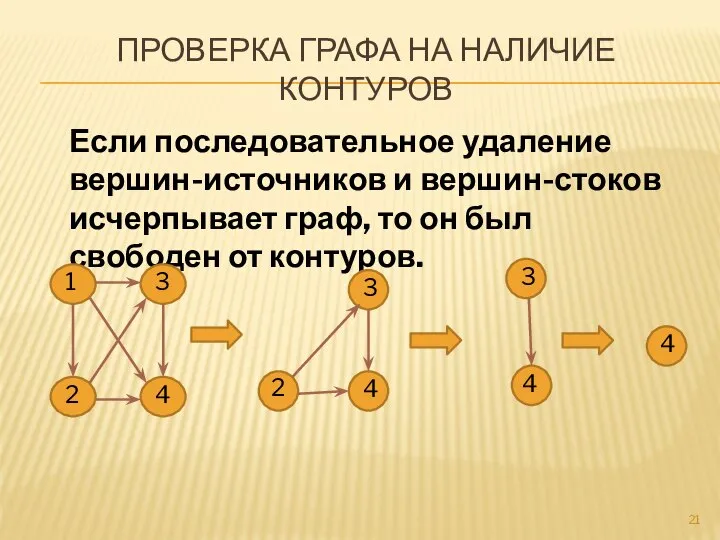
- 21. ПРОВЕРКА ГРАФА НА НАЛИЧИЕ КОНТУРОВ Если последовательное удаление вершин-источников и вершин-стоков исчерпывает граф, то он был
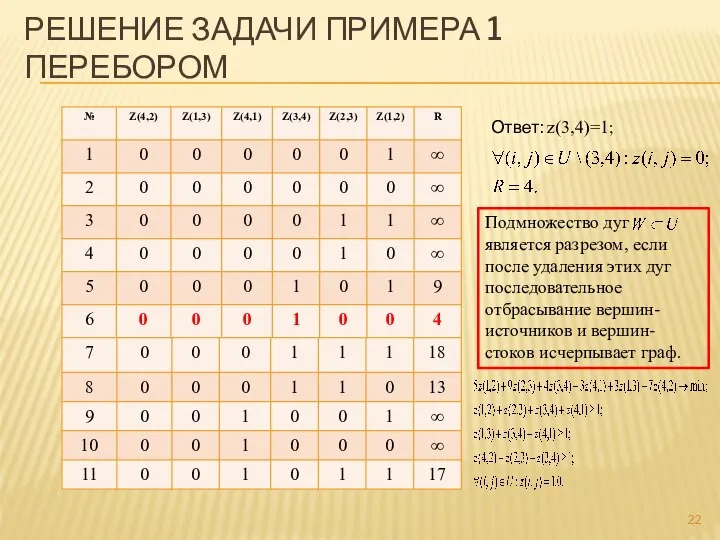
- 22. РЕШЕНИЕ ЗАДАЧИ ПРИМЕРА 1 ПЕРЕБОРОМ Ответ: z(3,4)=1; Подмножество дуг является разрезом, если после удаления этих дуг
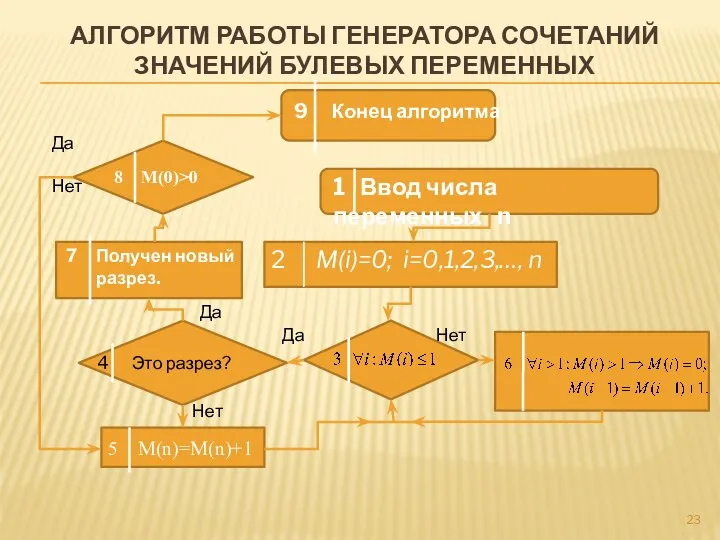
- 23. АЛГОРИТМ РАБОТЫ ГЕНЕРАТОРА СОЧЕТАНИЙ ЗНАЧЕНИЙ БУЛЕВЫХ ПЕРЕМЕННЫХ 1 Ввод числа переменных n 2 M(i)=0; i=0,1,2,3,…, n
- 24. ДОСТОИНСТВА И НЕДОСТАТКИ АЛГОРИТМА ГЕНЕРАЦИИ ВСЕХ СОЧЕТАНИЙ ЗНАЧЕНИЙ ВЕКТОРА БУЛЕВЫХ ПЕРЕМЕННЫХ Достоинства: Генерация всех сочетаний значений
- 25. САМОСТОЯТЕЛЬНО: Решить задачу о минимальном разрезе в бисвязном взвешенном орграфе, пользуясь графом персонального задания и приведенным
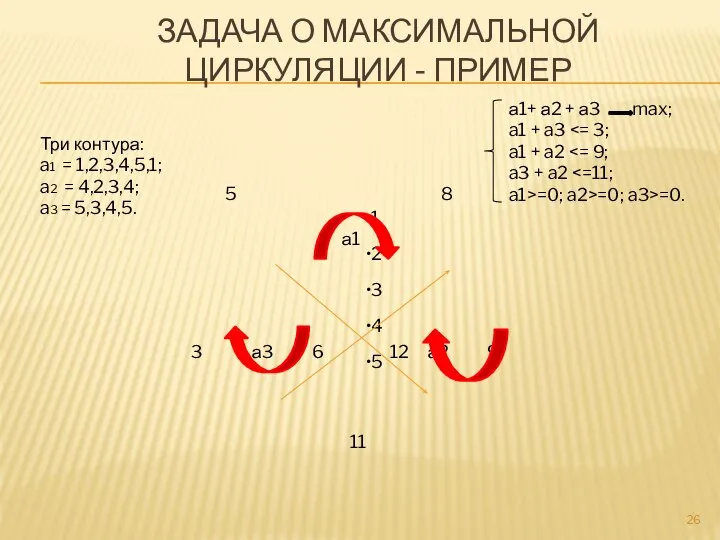
- 26. ЗАДАЧА О МАКСИМАЛЬНОЙ ЦИРКУЛЯЦИИ - ПРИМЕР 1 2 3 4 5 Три контура: a1 = 1,2,3,4,5,1;
- 27. ЗАДАЧА О МАКСИМАЛЬНОЙ ЦИРКУЛЯЦИИ В БИСВЯЗНОМ ГРАФЕ - ОБОЗНАЧЕНИЯ S(i,j) – поток по дуге (i,j) на
- 28. ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ ПОИСКА МАКСИМАЛЬНОЙ ЦИРКУЛЯЦИИ В БИСВЯЗНОМ ГРАФЕ
- 29. ТЕОРЕМА 1 В.Н. БУРКОВА Величина максимальной циркуляции на взвешенном бисвязном орграфе не превышает величины минимального разреза.
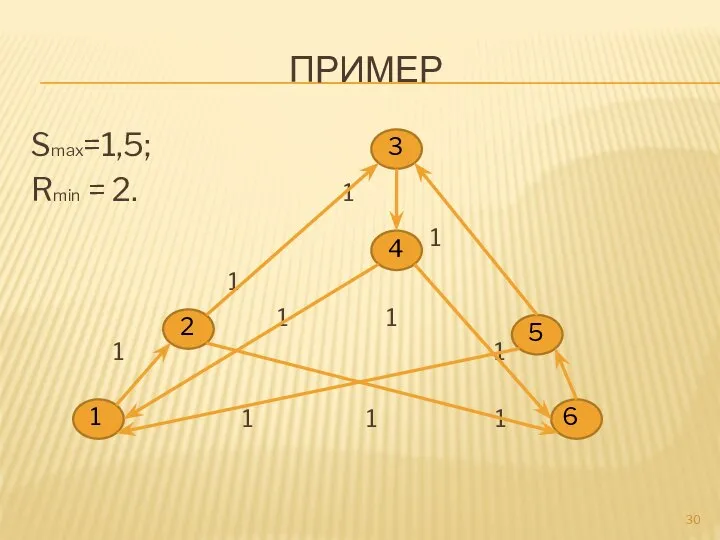
- 30. ПРИМЕР Smax=1,5; Rmin = 2. 1 1 1 1 1 1 1 1 1 1 1
- 31. ТЕОРЕМА 2 В.Н. БУРКОВА На планарных ориентированных взвешенных сильносвязных графах величина максимальной циркуляции всегда целочислена и
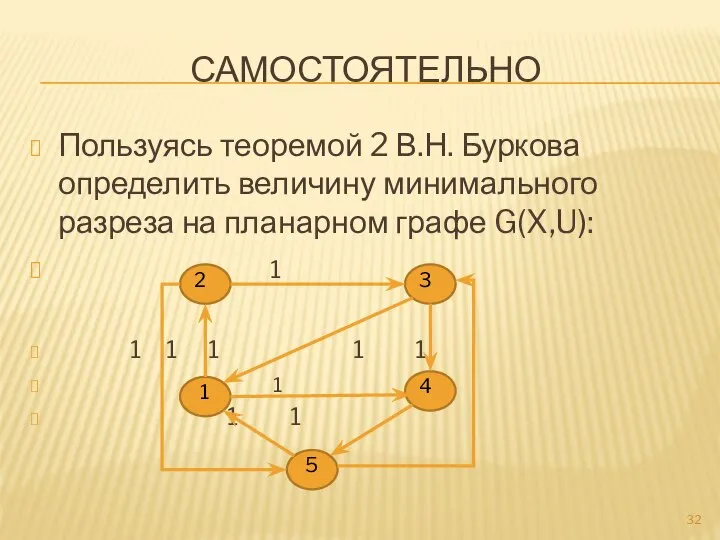
- 32. САМОСТОЯТЕЛЬНО Пользуясь теоремой 2 В.Н. Буркова определить величину минимального разреза на планарном графе G(X,U): 1 1
- 33. ТЕОРЕМА БУРКОВА № 3 Любой перестановке вершин бисвязного орграфа π={i1, i2, i3, ….in} отвечает разрез, состоящий
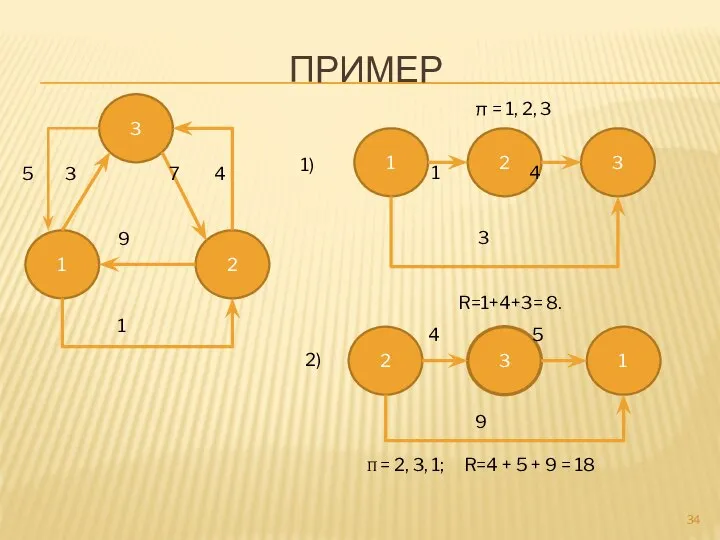
- 34. ПРИМЕР 3 2 1 5 3 7 4 9 1 1 2 3 π = 1,
- 35. ЛЕММА Любому разрезу в сильносвязном орграфе G(X,U) отвечает «своя» перестановка вершин π множества Х.
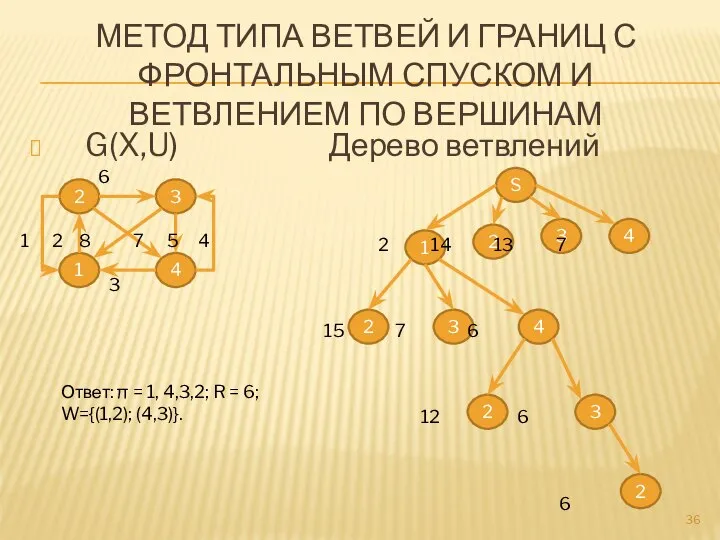
- 36. МЕТОД ТИПА ВЕТВЕЙ И ГРАНИЦ С ФРОНТАЛЬНЫМ СПУСКОМ И ВЕТВЛЕНИЕМ ПО ВЕРШИНАМ G(X,U) Дерево ветвлений 2
- 37. САМОСТОЯТЕЛЬНО Решить задачу о минимальном разрезе на взвешенном орграфе G(X,U), заданном матрицей M описанным выше методом:
- 39. Скачать презентацию























 Нормативная база УРО МООО «РСО»
Нормативная база УРО МООО «РСО» The Chidc's leoding maufacturer & cupperfier
The Chidc's leoding maufacturer & cupperfier Әндірістік тәжрибе бойынша есеп беру NGN
Әндірістік тәжрибе бойынша есеп беру NGN Massachusetts State House
Massachusetts State House «Ожившая кукла разных систем в известных театрах мира» «Куклы из тряпок, кусков дерева и бумажной массы совершенно явно оживают и действуют самостоятельно: они уже не следуют движениям управляющей ими руки, а напротив, сами ее направляют, у них свои жела
«Ожившая кукла разных систем в известных театрах мира» «Куклы из тряпок, кусков дерева и бумажной массы совершенно явно оживают и действуют самостоятельно: они уже не следуют движениям управляющей ими руки, а напротив, сами ее направляют, у них свои жела Культура Западной Европы
Культура Западной Европы Sakramenty święte
Sakramenty święte Презентация "Народные традиции в костюме Снегурочки" - скачать презентации по МХК
Презентация "Народные традиции в костюме Снегурочки" - скачать презентации по МХК Искусство комплимента
Искусство комплимента Стиль мода в нашей жизни
Стиль мода в нашей жизни Энергетическая дипломатия стран Латинской Америки и Карибского бассейна на современном этапе
Энергетическая дипломатия стран Латинской Америки и Карибского бассейна на современном этапе Маркетинговые возможности
Маркетинговые возможности Правила Дорожного Движения (ПДД)
Правила Дорожного Движения (ПДД) Крито-микенская культура
Крито-микенская культура Религия. Храм. Вера
Религия. Храм. Вера Социология как наука об обществе
Социология как наука об обществе Автор: Макарова Татьяна Павловна, учитель математики высшей категории ГБОУ СОШ №618 г. Москвы
Автор: Макарова Татьяна Павловна, учитель математики высшей категории ГБОУ СОШ №618 г. Москвы  Аэрофлот.Российские авиалинии
Аэрофлот.Российские авиалинии Технология производства метанола
Технология производства метанола Лимфатическая система, systema lymphatica, - часть кровеносной (венозной) системы
Лимфатическая система, systema lymphatica, - часть кровеносной (венозной) системы Организационная структура Общероссийского Союза Образования
Организационная структура Общероссийского Союза Образования Классификация поверхностей
Классификация поверхностей Язык культуры разнообразен
Язык культуры разнообразен Система права
Система права Директор МБОУ ДОД ДДТ п.г.т.Уренгой Пуровского района Коба Ирина Александровна
Директор МБОУ ДОД ДДТ п.г.т.Уренгой Пуровского района Коба Ирина Александровна Проектирование свайных фундаментов. (Лекция 22)
Проектирование свайных фундаментов. (Лекция 22) Політичні партії, громадсько-політичні об’єднання та рухи
Політичні партії, громадсько-політичні об’єднання та рухи Векторы.Линейные операции
Векторы.Линейные операции