Содержание
- 2. Гипотезы компактности и непрерывности
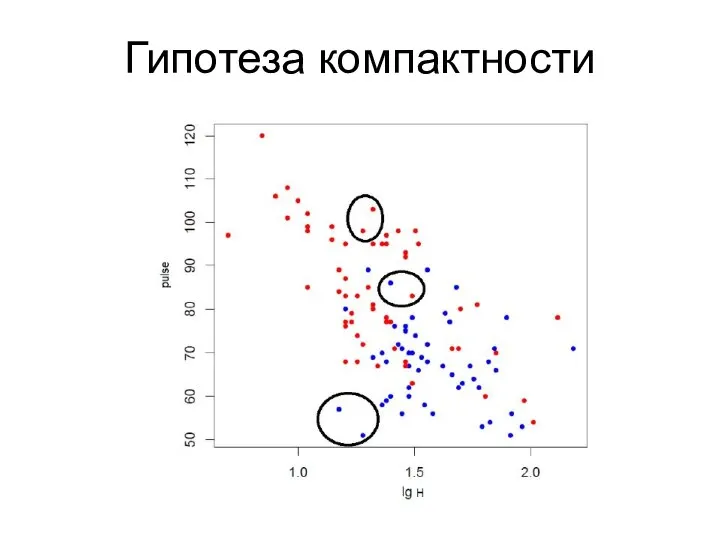
- 3. Гипотеза компактности
- 4. Постановка задачи классификации Исторически возникла из задачи машинного зрения, поэтому часто употребляемый синоним – распознавание образов.
- 5. Метод k ближайших соседей
- 6. Меры близости
- 7. Метод k ближайших соседей Выбор k
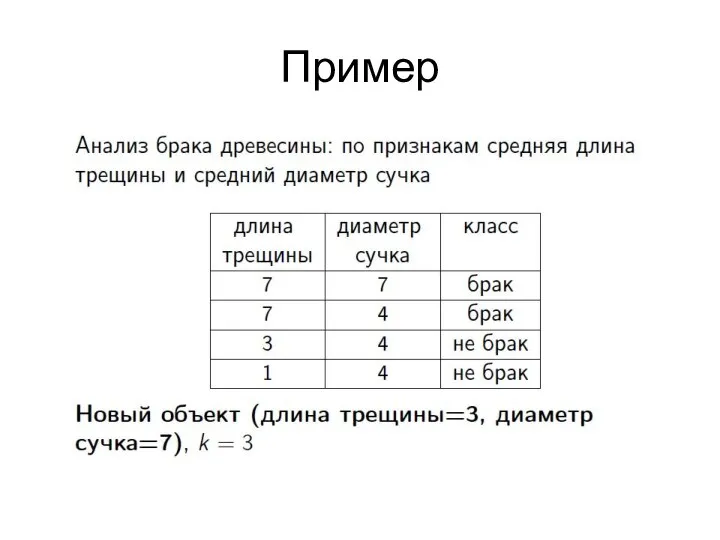
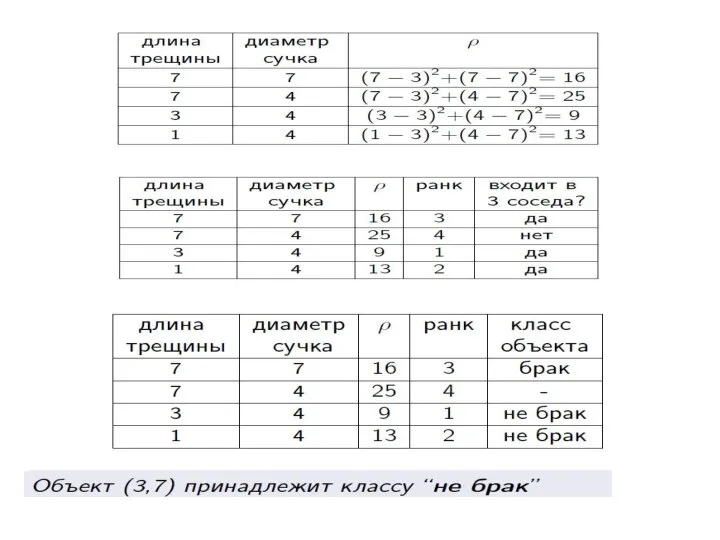
- 8. Пример
- 10. 1-правило Алгоритм построения 1-правил Простейший алгоритм формирования элементарных правил для классификации объекта. Он строит правила по
- 11. Example Let T be the following table Then BestRule(Vote,Office,T) is "case (X.Office) { House: predict (X.Vote==Yes);
- 12. Если переменная имеет вещественный тип, то количество возможных значений может быть бесконечно. Для решения этой проблемы
- 13. Томас Байес — английский математик, священник, член Лондонского королевского общества. Автор теоремы Байеса — одной из
- 14. Теорема Байеса и классификация (1)
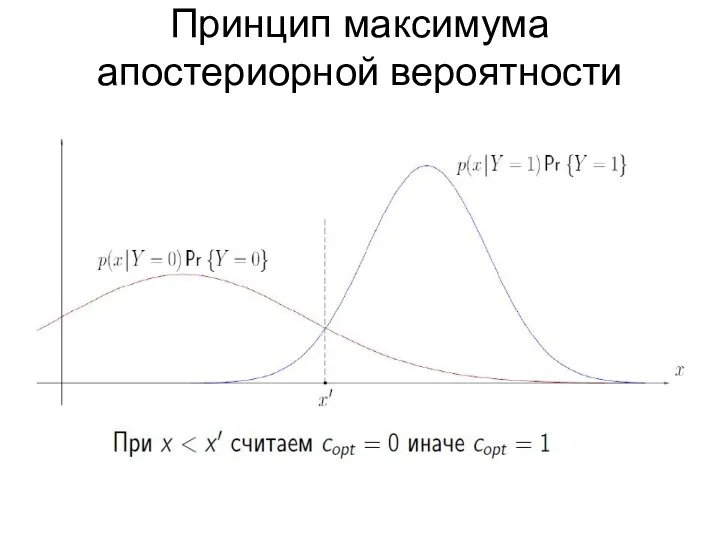
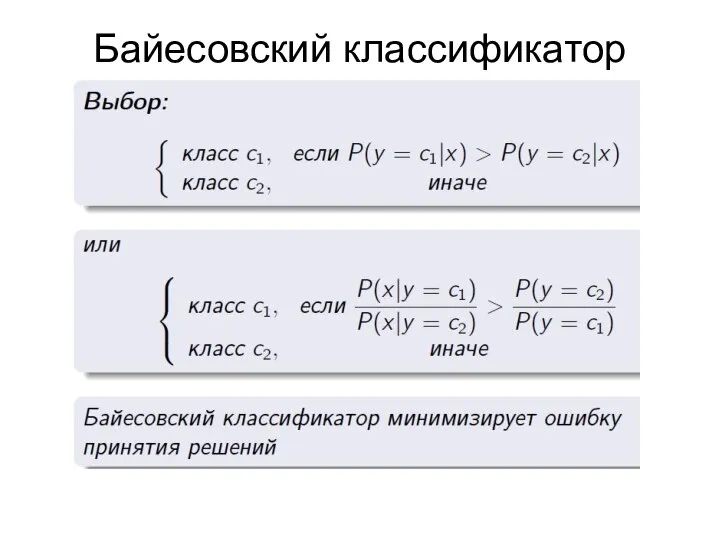
- 15. Принцип максимума апостериорной вероятности
- 16. Байесовский классификатор
- 17. Наивный байесовский классификатор Naive bayes
- 18. Оценка вероятностей в наивном байесовском классификаторе
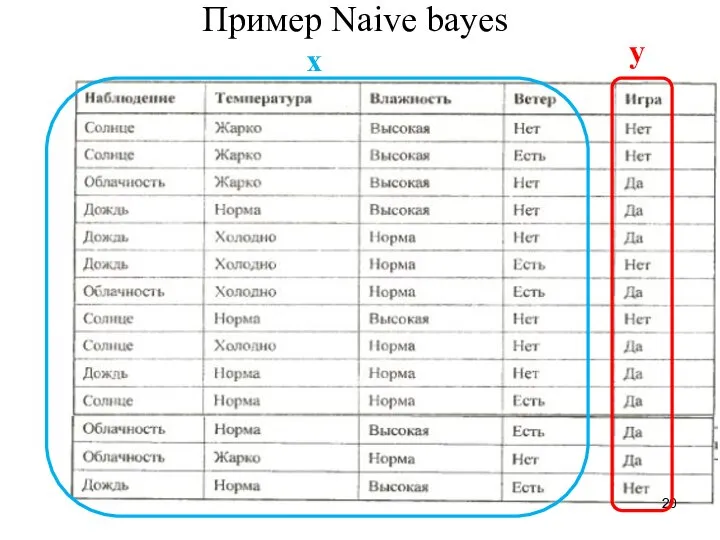
- 20. Пример Naive bayes y x
- 21. Метод Naive bayes. Необходимо определить, состоится ли игра при следующих значениях независимых переменных (событие Е):
- 22. Определяем условные вероятности
- 23. Метод Naive bayes. Априорные Вероятности есть отношение объектов из обучающей выборки, принадлежащих классу , к общему
- 24. Метод Naive bayes. Вычислим следующие апостериорные вероятности:
- 25. Метод Naive bayes. Подставляя соответствующие вероятности получим следующие значения: Вероятность не учитывается, т.к. при нормализации вероятностей
- 26. Метод Naive bayes. В данном случае можно утверждать, что при указанных условиях игра состоится с вероятностью:
- 27. Использование многомерного нормального распределения в задаче распознавания образов В статистической теории распознавания образов используется аппроксимация плотности
- 30. где В результате решающее правило распознавания имеет вид В случае линейного классификатора и рещающее правило примет
- 31. Сэр Ро́налд Э́йлмер Фи́шер (или Рональд, англ. Sir Ronald Aylmer Fisher, 17 февраля, 17 февраля 1890,
- 32. Линейный дискриминант Фишера
- 37. Классификация с использованием деревьев решений Лекция 3
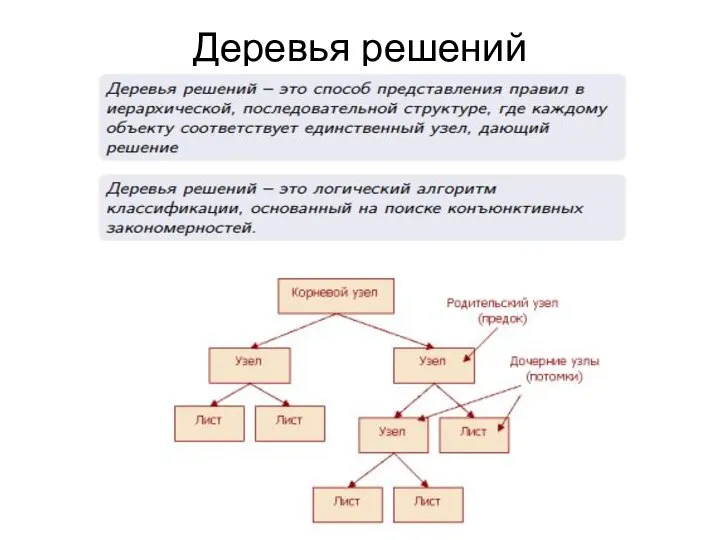
- 38. Деревья решений
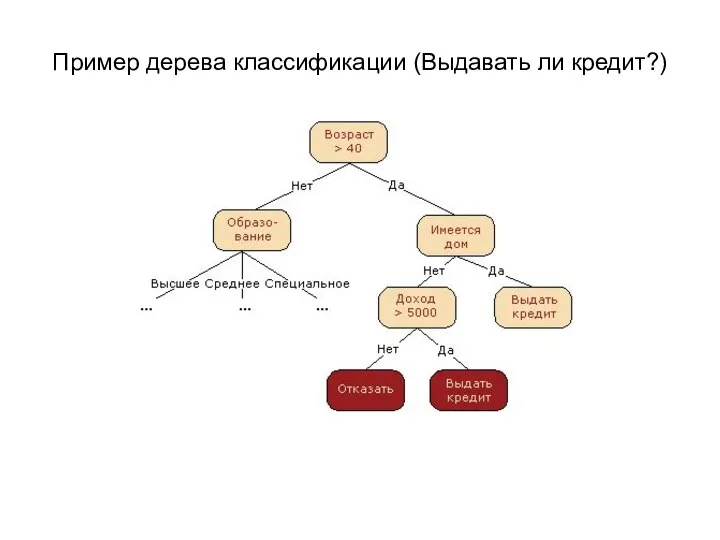
- 39. Пример дерева классификации (Выдавать ли кредит?)
- 40. Деревья решений Деревья решений - это способ представления классификационных правил в иерархической, последовательной структуре. Области применения
- 41. Обычно каждый узел дерева решений включает проверку одной независимой переменной. Иногда в узле дерева две независимые
- 42. Методика "Разделяй и властвуй" Методика основана на рекурсивном разбиении множества объектов из обучающей выборки на подмножества,
- 43. Множество Т содержит объекты, относящиеся к разным классам. В этом случае следует разбить множество Т на
- 44. Вопрос в том, какую зависимую переменную выбрать для начального разбиения. От этого целиком зависит качество получившегося
- 45. Конструирование дерева решений Процесс конструирования дерева решений Рассматриваемая нами задача классификации относится к стратегии обучения с
- 46. Критерии расщепления Процесс создания дерева происходит сверху вниз, т.е. является нисходящим. В ходе процесса алгоритм должен
- 47. Алгориты построения деревьв Есть различные способы выбирать очередной атрибут: Алгоритм ID3Алгоритм ID3, где выбор атрибута происходит
- 48. Алгоритмы ID3 и С4.5 Алгоритм ID3 [32] был предложен Россом Куинланом в 1986 г. и основывался
- 49. Алгоритм ID3 ID3 (Iterative Dichotomiser 3) is an algorithm) is an algorithm invented by Ross Quinlan
- 50. Критерий расщепления ID3
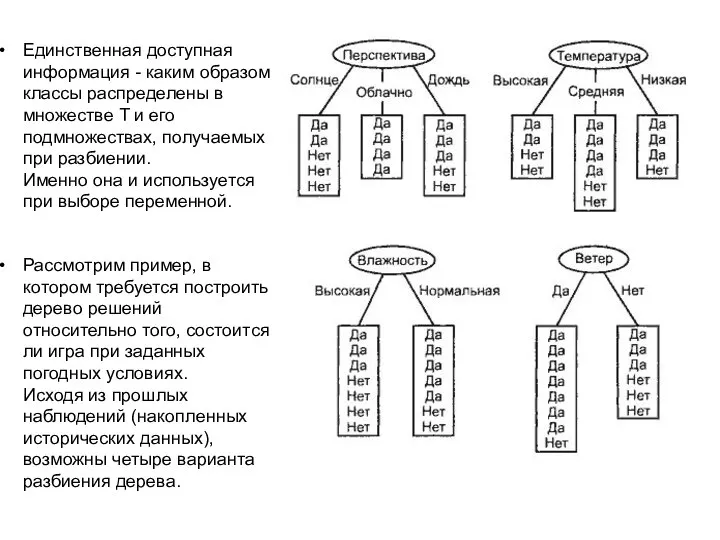
- 51. Единственная доступная информация - каким образом классы распределены в множестве T и его подмножествах, получаемых при
- 52. Пусть freq(cr,I) - число объектов из обучающей выборки, относящихся к классу cr. Тогда вероятность того, что
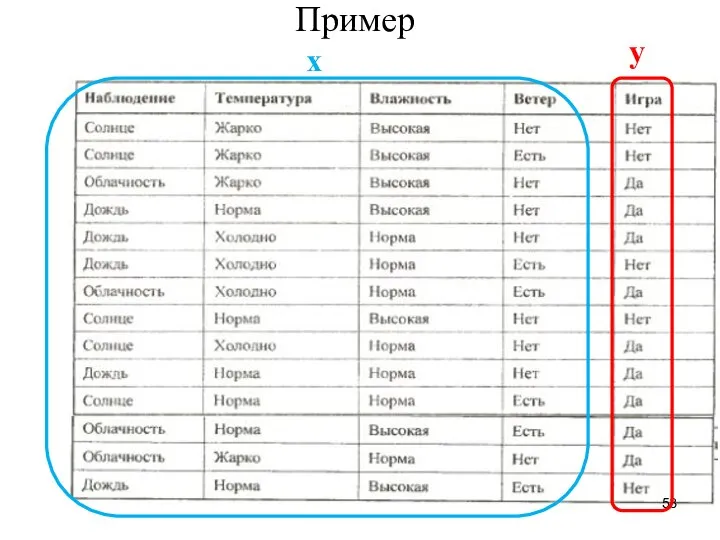
- 53. Пример y x
- 54. Поскольку используется логарифм с двоичным основанием, то это выражение даёт количественную оценку в битах. Для оценки
- 55. Например, для переменной "Наблюдение", оценка будет следующей: бит. бит. бит. бит. Критерием для выбора атрибута (зависимой
- 56. В нашем примере значение Gain для независимой переменной "Наблюдение" (перспектива) будет равно: Gain(перспектива) = Info(I) -
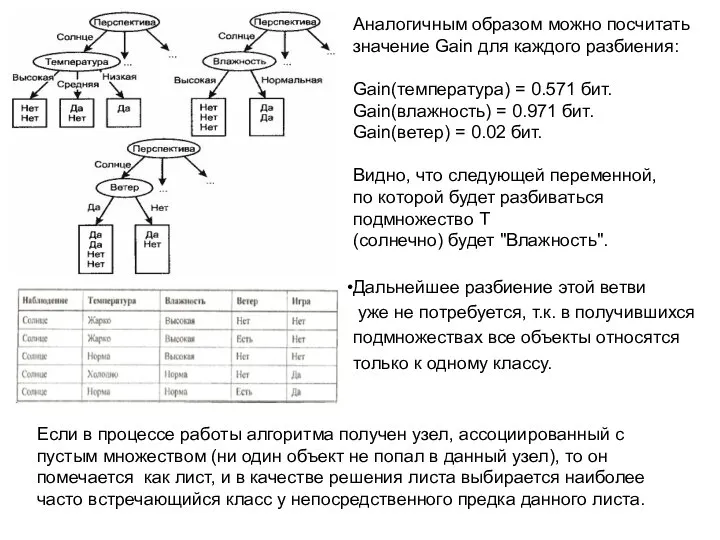
- 57. Аналогичным образом можно посчитать значение Gain для каждого разбиения: Gain(температура) = 0.571 бит. Gain(влажность) = 0.971
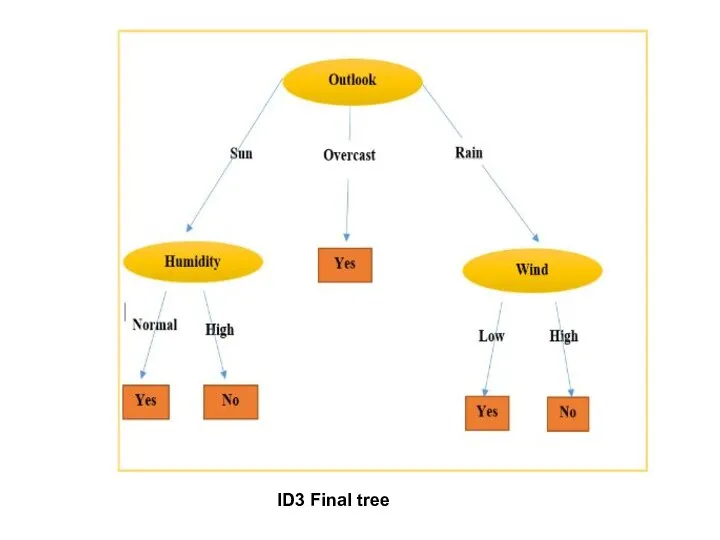
- 58. ID3 Final tree
- 59. Алгоритм C4.5 C4.5 is an algorithm used to generate a decision tree is an algorithm used
- 60. Один из недостатков алгоритма ID3 является то, что он некорректно работает с атрибутами, имеющими уникальные значения
- 61. При условии, что имеется k классов и n - число объектов в обучающей выборке и одновременно
- 62. Алгоритм CART
- 63. Обучение дерева решений относится к классу обучения с учителем, то есть обучающая и тестовая выборки содержат
- 64. Если набор Т разбивается на две части Т1 и Т2 с числом примеров в каждом N1
- 65. Процедура разбиения CART Вектор предикторных переменных, подаваемый на вход дерева может содержать как числовые (порядковые) так
- 66. Процедура разбиения CART
- 67. Механизм отсечения дерева Механизм отсечения дерева, оригинальное название minimal cost-complexity tree pruning, – наиболее серьезное отличие
- 68. Определим полную стоимость (оценку/показатель затраты-сложность) дерева Т как: где |T| – число листов (терминальных узлов) дерева,
- 69. Определим Tmax – максимальное по размеру дерево, которое предстоит обрезать. Если мы зафиксируем значение α тогда
- 71. Скачать презентацию






































![Алгоритмы ID3 и С4.5 Алгоритм ID3 [32] был предложен Россом Куинланом](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/657503/slide-47.jpg)

















 Естествознание-наука о природе
Естествознание-наука о природе Гормональное расписание моего организма
Гормональное расписание моего организма Ядовитые растения. Для дошкольников
Ядовитые растения. Для дошкольников Разработка урока по биологии для 8 класса на тему: «Значение физических упражнений для формирования аппарата опоры и движен
Разработка урока по биологии для 8 класса на тему: «Значение физических упражнений для формирования аппарата опоры и движен Микроскоп и его строение. Работа с микроскопом
Микроскоп и его строение. Работа с микроскопом Методы генетики человека
Методы генетики человека  Птицы нашего двора. 2 класс
Птицы нашего двора. 2 класс Флора. Методы сбора и анализа флористических данных
Флора. Методы сбора и анализа флористических данных Тема урока Тема урока Приспособленность организмов к условиям внешней среды как результат действия естественного отбора. Ав
Тема урока Тема урока Приспособленность организмов к условиям внешней среды как результат действия естественного отбора. Ав КИНЕЗИОЛОГИЯ КИНЕЗИОЛОГИЯ
КИНЕЗИОЛОГИЯ КИНЕЗИОЛОГИЯ  Принципы построения композиций из горшечных растений
Принципы построения композиций из горшечных растений Зелёная аптека
Зелёная аптека Дары осени
Дары осени Регуляция работы сердца и сосудов. Автоматизм сердечной деятельности
Регуляция работы сердца и сосудов. Автоматизм сердечной деятельности Презентация на тему "Приспособленность организмов" - скачать презентации по Биологии
Презентация на тему "Приспособленность организмов" - скачать презентации по Биологии Сердечно сосудистая, дыхательная и нервная
Сердечно сосудистая, дыхательная и нервная Фауна Таймырского полуострова и островов Северного Ледовитого океана
Фауна Таймырского полуострова и островов Северного Ледовитого океана Бактерии друзья или враги человека? ВЫПОЛНИЛА РАБОТУ АСТРАХАНЦЕВА ЮЛИЯ ученица 2-б класса МОУ «ПСОШ»
Бактерии друзья или враги человека? ВЫПОЛНИЛА РАБОТУ АСТРАХАНЦЕВА ЮЛИЯ ученица 2-б класса МОУ «ПСОШ»  Гомологичные и аналогичные органы
Гомологичные и аналогичные органы Знатоки природы. Викторина
Знатоки природы. Викторина Строение печени
Строение печени 7c30d1bebe0e49b184755872180c6517 (1)
7c30d1bebe0e49b184755872180c6517 (1) Презентация на тему "Лишайники" - скачать презентации по Биологии
Презентация на тему "Лишайники" - скачать презентации по Биологии Vitaminas Hidrossolúveis B6; B7; B9; B12; C
Vitaminas Hidrossolúveis B6; B7; B9; B12; C Некоторые семейства класса костных рыб
Некоторые семейства класса костных рыб Врождённое поведение человека
Врождённое поведение человека Биогеоценозы и биоценозы. Презентация Климовой Ирины Генриховны учителя биологии I квалификационной категории МОУ СОШ №11 г.Севе
Биогеоценозы и биоценозы. Презентация Климовой Ирины Генриховны учителя биологии I квалификационной категории МОУ СОШ №11 г.Севе Презентация на тему "Вирусы" - скачать презентации по Биологии
Презентация на тему "Вирусы" - скачать презентации по Биологии