Содержание
- 2. Введение в анализ временных рядов 2 Матрица «объект-свойство»: n = 1, T > 1 – временные
- 3. Основные факторы, формирующие временной ряд 3 1. Долговременные – общая тенденция изменения признака, как прави-ло, монотонная.
- 4. Основные задачи анализа временных рядов 4 Определить, какие факторы (долговременные, сезонные, циклические, случайные) присутствуют в модели.
- 5. Неслучайная составляющая временного ряда 5 Необходимо выявить (желательно автоматически) факт наличия / отсут-ствия неслучайной (т.е. зависящей
- 6. Критерий серий, построенный на медиане 6 1. Переходим к вариационному ряду (сортируем в порядке возрастания): y1
- 7. Критерий восходящих и нисходящих серий 7 1. На основе исходного ряда записываем серии из «+» и
- 8. Критерий Аббе (квадратов последовательных разностей) 8 1. Подсчитываем эмпирическое значение критерия 2. Находим критическую точку 3.
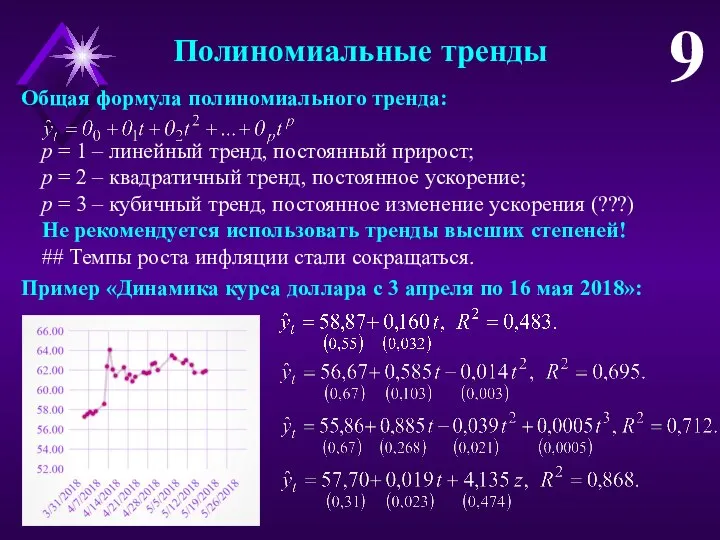
- 9. Полиномиальные тренды 9 Общая формула полиномиального тренда: p = 1 – линейный тренд, постоянный прирост; p
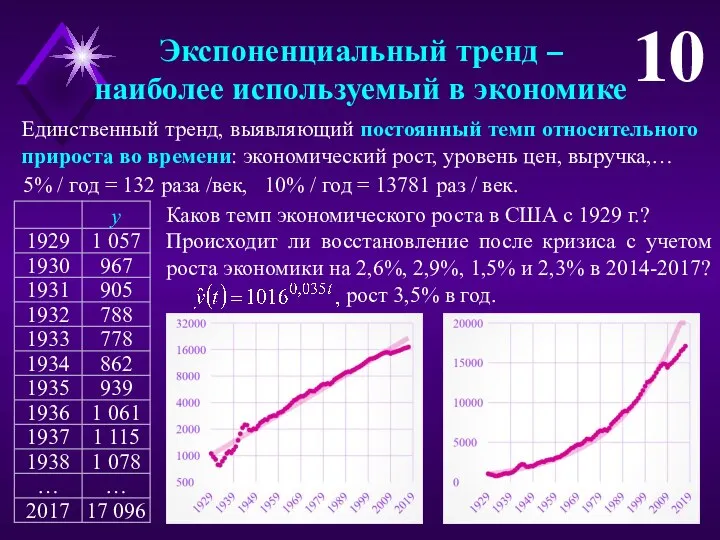
- 10. Экспоненциальный тренд – наиболее используемый в экономике 10 Каков темп экономического роста в США с 1929
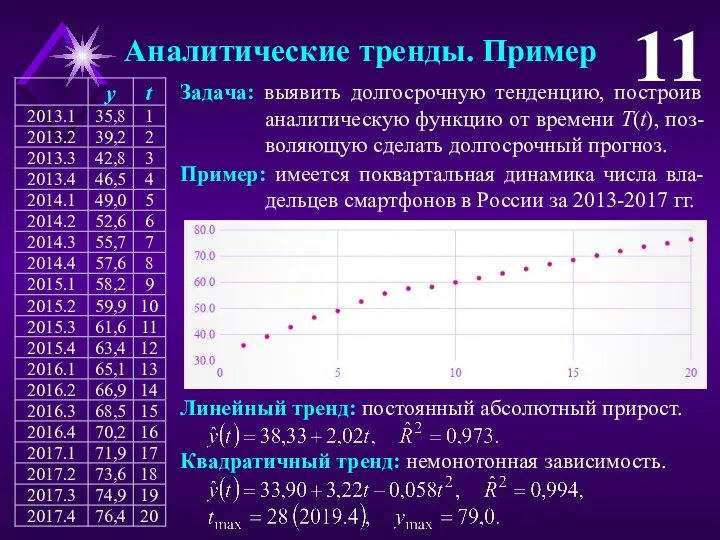
- 11. Аналитические тренды. Пример 11 Задача: выявить долгосрочную тенденцию, построив аналитическую функцию от времени T(t), поз-воляющую сделать
- 12. Аналитические тренды. Пример 12 Логарифмический тренд: наиболее медленный неог-раниченный рост, функция определена только для по-ложительных t,
- 13. Аналитические тренды. Прогноз 13
- 14. Алгоритмические тренды. Скользящее среднее 14 Задача: сглаживание значений временного ряда по m предыдущим, m последующим и
- 15. Наилучшие значения весовых коэффициентов wk 15 Наилучшие (в смысле МНК) значения весовых коэффициентов выби-раем в зависимости
- 16. Вывод весовых коэффициентов для квадратичного полинома 16 Решение задачи поиска наилучших весовых коэффициентов рассмотрим на примере
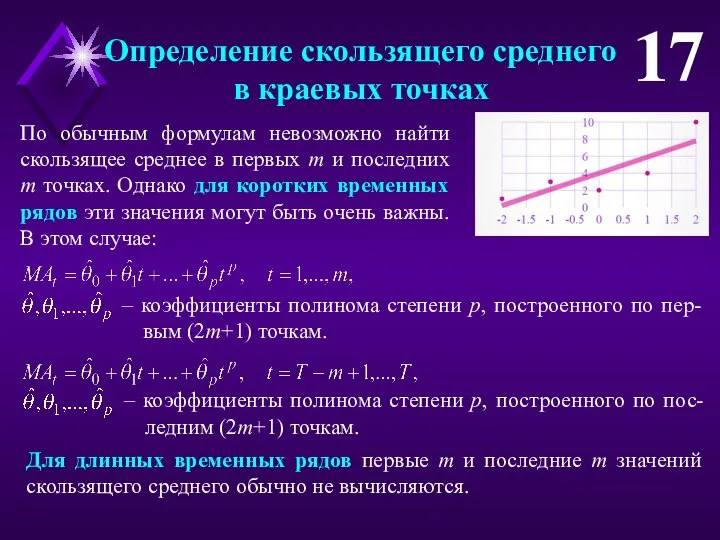
- 17. Определение скользящего среднего в краевых точках 17 По обычным формулам невозможно найти скользящее среднее в первых
- 18. Определение скользящего среднего по четному числу точек 18 Скользящее среднее иногда применяется для устранения сезонных и
- 19. Экспоненциально взвешенное скользящее среднее 19 Скользящее среднее применялось для интерполяции данных (усред-нения внутри диапазона временного ряда).
- 20. Сезонность и ее устранение с помощью скользящего среднего 20 Сезонность: – аддитивная форма, – мультипликативная форма.
- 21. Численный пример. Аддитивная сезонность 21 Корректировка: Сезонность: Тренд: Точность модели:
- 22. Численный пример. Мультипликативная сезонность 22 Корректировка: Сезонность: Тренд: Точность модели:
- 24. Скачать презентацию

















 Математическое моделирование поведения продавца в условиях монополии
Математическое моделирование поведения продавца в условиях монополии Предмет и метод экономической теории. (Тема 1)
Предмет и метод экономической теории. (Тема 1) Перспективы роста российской экономики
Перспективы роста российской экономики Производство и издержки
Производство и издержки Характеристика основных экономических школ 20-21 века
Характеристика основных экономических школ 20-21 века Инвестиционный климат Иркутской области
Инвестиционный климат Иркутской области Главные вопросы экономики
Главные вопросы экономики Экономика.Понятие и основные принципы
Экономика.Понятие и основные принципы Модели олигополии и их проявление в современной экономике
Модели олигополии и их проявление в современной экономике Интеграция
Интеграция Опыт Березовского муниципального района по реализации проекта «Сохраним семью – сбережем Россию»
Опыт Березовского муниципального района по реализации проекта «Сохраним семью – сбережем Россию» Особенности поведения хозяйствующих субъектов в Республике Беларусь БА-11 Лучиц Даниил 1 курс
Особенности поведения хозяйствующих субъектов в Республике Беларусь БА-11 Лучиц Даниил 1 курс Мировые экономические проблемы и научно-технический прогресс
Мировые экономические проблемы и научно-технический прогресс Инвестиционные риски. Характеристики методов учета неопределенности инвестиционного проекта. (Тема 9)
Инвестиционные риски. Характеристики методов учета неопределенности инвестиционного проекта. (Тема 9) Собівартість продукції
Собівартість продукції Факторы производства и факторные доходы
Факторы производства и факторные доходы Анализ динамики состояния человеческих ресурсов Костромской области
Анализ динамики состояния человеческих ресурсов Костромской области Бухгалтерский баланс
Бухгалтерский баланс Трансакционные издержки
Трансакционные издержки Україна і Африка
Україна і Африка Сутегі отыны бензинге қарағанда арзан болады
Сутегі отыны бензинге қарағанда арзан болады Международная экономическая интеграция
Международная экономическая интеграция Управління прибутком підприємства в умовах цифрової економіки
Управління прибутком підприємства в умовах цифрової економіки Модели олигополии и их проявление в современной экономике
Модели олигополии и их проявление в современной экономике Экономический рост и развитие. Понятие ВВП
Экономический рост и развитие. Понятие ВВП Troika Venture Funds Раскрытие российского потенциала в инновационных технологиях
Troika Venture Funds Раскрытие российского потенциала в инновационных технологиях Экономика. Сущность экономического цикла и его фазы
Экономика. Сущность экономического цикла и его фазы Сущность, виды и формы внешнеэкономической деятельности. (Лекция 1.2)
Сущность, виды и формы внешнеэкономической деятельности. (Лекция 1.2)