Содержание
- 2. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Univariate time series models Univariate time series modelling
- 3. Quantitative Economic Analysis – 2016, Dr. Kashif Saleem (UOWD) Let ut (t=1,2,3,...) be a sequence of
- 4. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) An autoregressive model of order p, an AR(p)
- 5. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) By combining the AR(p) and MA(q) models, we
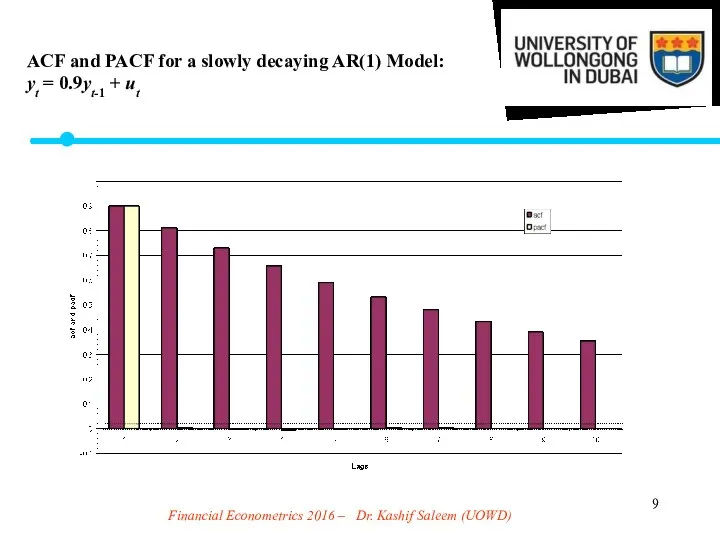
- 6. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) An autoregressive process has a geometrically decaying acf
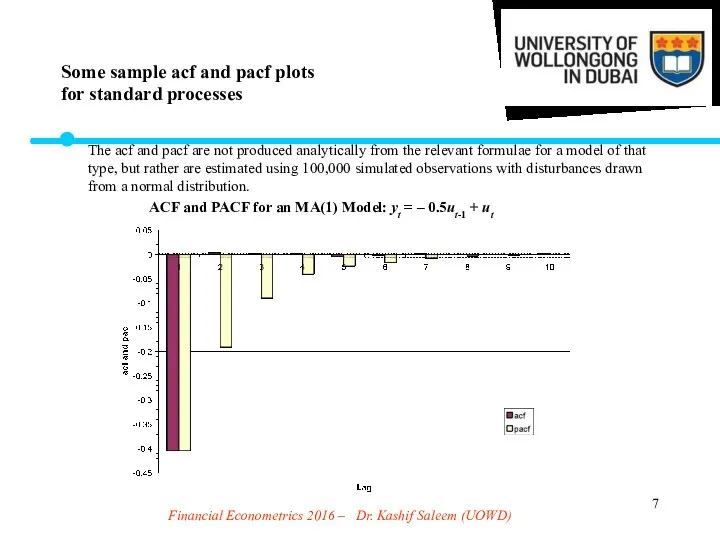
- 7. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) The acf and pacf are not produced analytically
- 8. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) ACF and PACF for an MA(2) Model: yt
- 9. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) ACF and PACF for a slowly decaying AR(1)
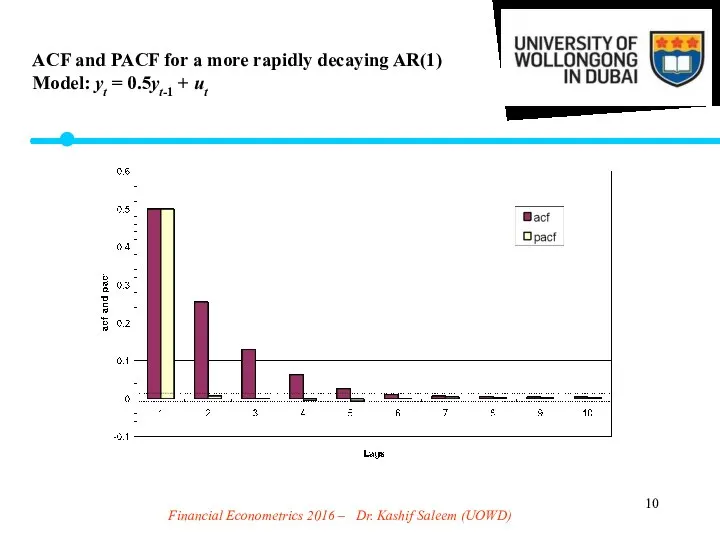
- 10. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) ACF and PACF for a more rapidly decaying
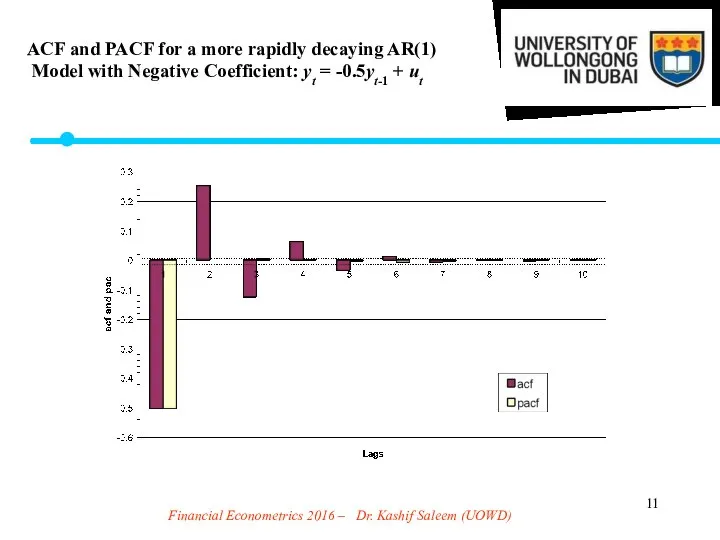
- 11. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) ACF and PACF for a more rapidly decaying
- 12. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) ACF and PACF for a Non-stationary Model (i.e.
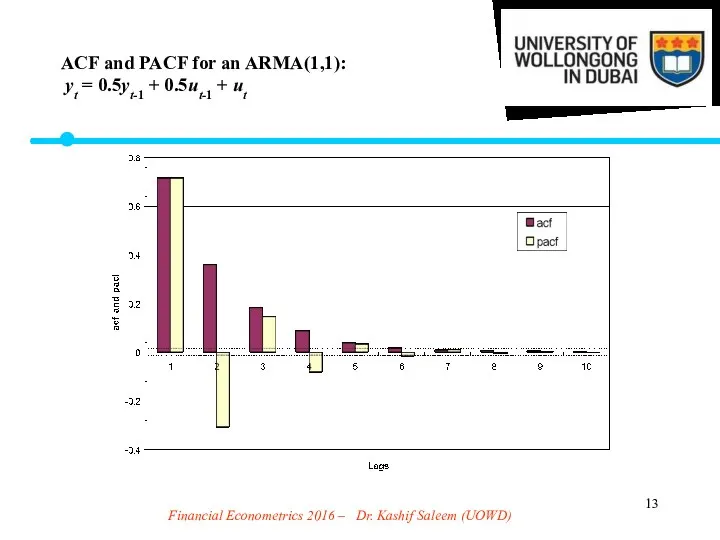
- 13. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) ACF and PACF for an ARMA(1,1): yt =
- 14. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Box and Jenkins (1970) were the first to
- 15. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Step 2: - Estimation of the parameters -
- 16. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Identification would typically not be done using acf’s.
- 17. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) The three most popular criteria are Akaike’s (1974)
- 18. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) As distinct from ARMA models. The I stands
- 19. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Another modelling and forecasting technique How much weight
- 20. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Forecasting = prediction. An important test of the
- 21. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Expect the “forecast” of the model to be
- 22. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Models for Forecasting Time Series Models The current
- 23. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) An MA(q) only has memory of q. e.g.
- 24. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) ft, 1 = E(yt+1 | t ) =
- 25. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Say we have estimated an AR(2) yt =
- 26. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) ft, 3 = E(yt+3 | t ) =
- 27. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Some of the most popular criteria for assessing
- 28. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) A natural generalisation of autoregressive models popularised by
- 29. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) One important feature of VARs is the compactness
- 30. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) This model can be extended to the case
- 31. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Advantages of VAR Modelling - Do not need
- 32. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Choosing the Optimal Lag Length for a VAR
- 33. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Choosing the Optimal Lag Length for a VAR
- 34. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Information Criteria for VAR Lag Length Selection Multivariate
- 35. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Block Significance and Causality Tests It is likely
- 36. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Block Significance and Causality Tests (cont’d) Each of
- 37. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Impulse Responses VAR models are often difficult to
- 38. Financial Econometrics 2016 – Dr. Kashif Saleem (UOWD) Variance Decompositions Variance decompositions offer a slightly different
- 39. Home Assignment Vector Autoregressive Model: Run a VAR (3) model by using exchange rate data on
- 41. Скачать презентацию

































 Экономические системы
Экономические системы Стратегия и тактика ценообразования
Стратегия и тактика ценообразования США в глобальной экономике и роли в странах АТР
США в глобальной экономике и роли в странах АТР Этапы развития экономической науки
Этапы развития экономической науки Международные экономические организации
Международные экономические организации Экономическая безопасность России
Экономическая безопасность России Типология рынков
Типология рынков Лекция № 5. Вмешательство государства и общественное благосостояние
Лекция № 5. Вмешательство государства и общественное благосостояние Натуральное хозяйство. Товарное производство
Натуральное хозяйство. Товарное производство Экономический механизм возникновения кризисных явлений в деятельности организации
Экономический механизм возникновения кризисных явлений в деятельности организации Презентация Функционалистская теория происхождения культуры
Презентация Функционалистская теория происхождения культуры Предложение инвестиционного фонда Pinnacle Absolute Return Global Alpha Fund
Предложение инвестиционного фонда Pinnacle Absolute Return Global Alpha Fund Мировая экономика
Мировая экономика Меркантилизм и физиократия
Меркантилизм и физиократия Экономические задачи ЕГЭ
Экономические задачи ЕГЭ Коррупция – экономико-правовое обоснование
Коррупция – экономико-правовое обоснование Резервы и пути повышения рентабельности машиностроительного предприятия
Резервы и пути повышения рентабельности машиностроительного предприятия Taiwan’s economic situation
Taiwan’s economic situation Спрос, предложение и рыночное равновесие
Спрос, предложение и рыночное равновесие Потребности, блага, экономический выбор
Потребности, блага, экономический выбор Теория систем и системный анализ в экономике. Социально-экономические системы
Теория систем и системный анализ в экономике. Социально-экономические системы Финансовая грамотность и ее проецирование на профессиональную деятельность
Финансовая грамотность и ее проецирование на профессиональную деятельность Analiza strategiei de dezvoltare a turismului în România și Rep.Moldova
Analiza strategiei de dezvoltare a turismului în România și Rep.Moldova Class 4 The Ownership of Nature Objects and Natural Resources
Class 4 The Ownership of Nature Objects and Natural Resources Социальная политика государства. Политика доходов. Экономика домашнего хозяйства, семьи
Социальная политика государства. Политика доходов. Экономика домашнего хозяйства, семьи Экономика: наука и хозяйство
Экономика: наука и хозяйство Рынок инноваций
Рынок инноваций Основные понятия теории экономики и управления безопасностью
Основные понятия теории экономики и управления безопасностью