ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В МАКРОЭКОНОМИКЕ
Основой большинства макроэкономических моделей линейного программирования является
модель межотраслевого баланса, разработанная В. Леонтьевым в 20-х годах прошлого столетия. Модель получила название по имени автора, а сам В. Леонтьев получил за ее разработку Нобелевскую премию, в области экономики.
Сущность этой модели состоит в следующем. Предполагается, что весь производственный комплекс страны (или любой крупной экономической системы) разделен на n отраслей. Каждая отрасль выпускает однородную продукцию (продукцию одного типа), но разные отрасли выпускают разную продукцию. Таким образом, в целом выпускается n типов продукции.
В процессе производства каждая отрасль использует продукцию других отраслей и, в свою очередь, снабжает другие отрасли своей продукцией. Кроме того, каждая отрасль выпускает продукцию, которая потребляется в непроизводственной сфере (сфера потребления, создание запасов).
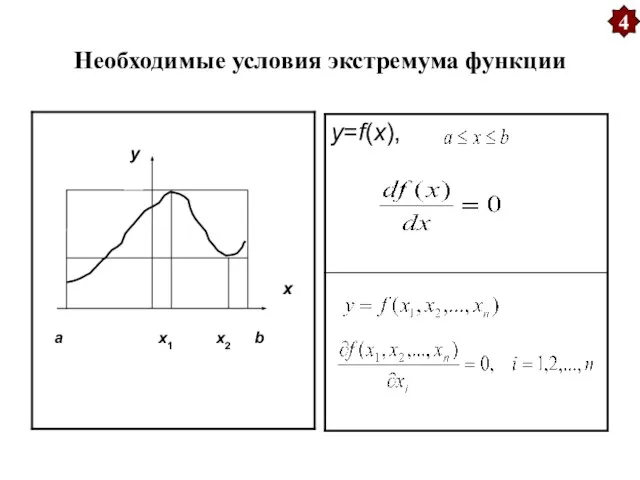
Полагается, что для отрасли i известно количество aij ее продукции, которое используется для производства единицы продукции отрасли j и количество Ci единиц этой продукции используемой в непроизводственной сфере (накопление, потребление). Требуется определить валовой объем продукции i-й отрасли, обеспечивающий выполнение условия межотраслевого баланса





















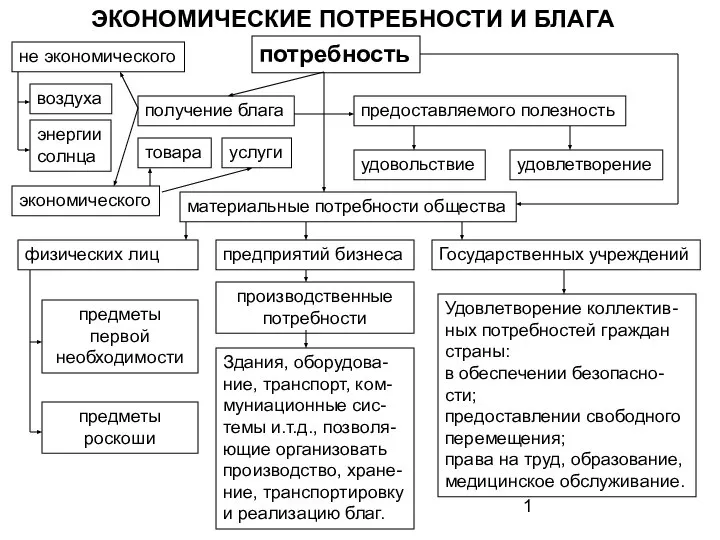 Экономические потребности и блага
Экономические потребности и блага Себестоимость продукции
Себестоимость продукции Генеральноцелевое, стратегическое и оперативное планирование
Генеральноцелевое, стратегическое и оперативное планирование Межличностные конфликты в семье Подготовила: Порошина Лидия Владимировна, студентка очной формы обучения юридического факульте
Межличностные конфликты в семье Подготовила: Порошина Лидия Владимировна, студентка очной формы обучения юридического факульте Критический анализ модели «кейнсианского креста». Рецессионный и инфляционный разрыв
Критический анализ модели «кейнсианского креста». Рецессионный и инфляционный разрыв Ефективність використання авіації при виконанні робіт з патрулювання трубопроводів
Ефективність використання авіації при виконанні робіт з патрулювання трубопроводів Глобальный цифровой рынок и место России на нём
Глобальный цифровой рынок и место России на нём Экономика стран переселенческого капитализма (Австралия, Израиль, Новая Зеландия, ЮАР)
Экономика стран переселенческого капитализма (Австралия, Израиль, Новая Зеландия, ЮАР) Универсальная комплексная присадка для топлив “NagroBoost”
Универсальная комплексная присадка для топлив “NagroBoost” Экономический потенциал единой таможенной территории Таможенного союза ЕАЭС. Национальное богатство и экономический потенциал
Экономический потенциал единой таможенной территории Таможенного союза ЕАЭС. Национальное богатство и экономический потенциал Тема 6. Теорія і практика соціально-економічних досліджень
Тема 6. Теорія і практика соціально-економічних досліджень Методические основы экономического анализа
Методические основы экономического анализа Создание и управление деятельностью предприятия по производству оборудования для пчеловодов
Создание и управление деятельностью предприятия по производству оборудования для пчеловодов Теория потребительского выбора
Теория потребительского выбора Решаем задание 10 по обществознанию. Практика
Решаем задание 10 по обществознанию. Практика «Как убедить каждого продавца оценивать свою недвижимость по рыночной стоимости» 02.07.2012. - презентация
«Как убедить каждого продавца оценивать свою недвижимость по рыночной стоимости» 02.07.2012. - презентация Экономика здравоохранения как наука и предмет преподавания
Экономика здравоохранения как наука и предмет преподавания Социально-экономический мониторинг рекреационных объектов Сочинского национально парка
Социально-экономический мониторинг рекреационных объектов Сочинского национально парка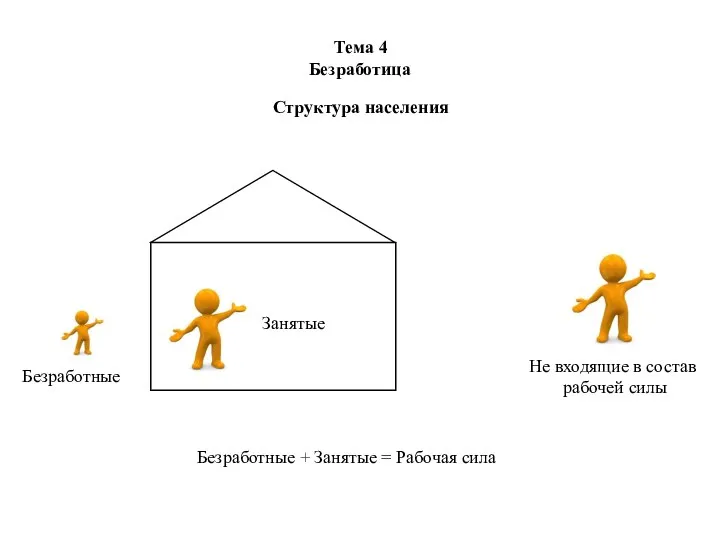 Безработица. Структура населения
Безработица. Структура населения Финансы организаций. Прибыль организаций. (Тема 3.6)
Финансы организаций. Прибыль организаций. (Тема 3.6) Роль государства в экономике
Роль государства в экономике Классификация и кодирование товаров. (Лекция 2)
Классификация и кодирование товаров. (Лекция 2) Система национальных счетов (СНС) и макроэкономические показатели
Система национальных счетов (СНС) и макроэкономические показатели Формы общественного хозяйства. Товар и деньги
Формы общественного хозяйства. Товар и деньги Инвестиционные предложения
Инвестиционные предложения Презентация Деньги и их функции
Презентация Деньги и их функции Описание и анализ выбранного объекта исследования. Цель и задачи
Описание и анализ выбранного объекта исследования. Цель и задачи Экономическое содержание государственных и муниципальных финансов, их значение
Экономическое содержание государственных и муниципальных финансов, их значение