Содержание
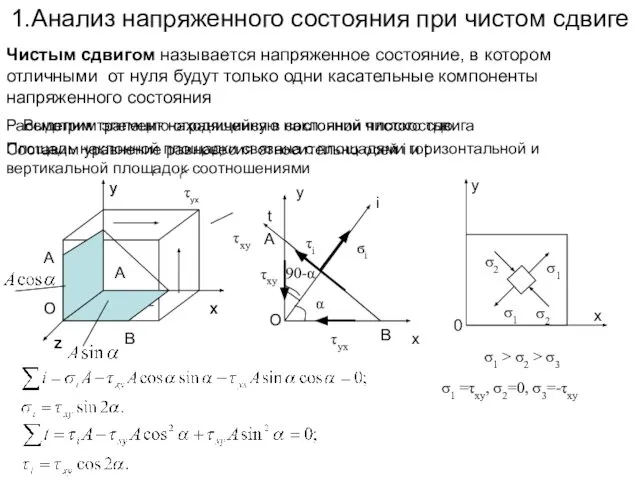
- 2. 1.Анализ напряженного состояния при чистом сдвиге Чистым сдвигом называется напряженное состояние, в котором отличными от нуля
- 3. Закон Гука при чистом сдвиге Так как нормальные компоненты тензора напряжений равны нулю, то: Потенциальная энергия
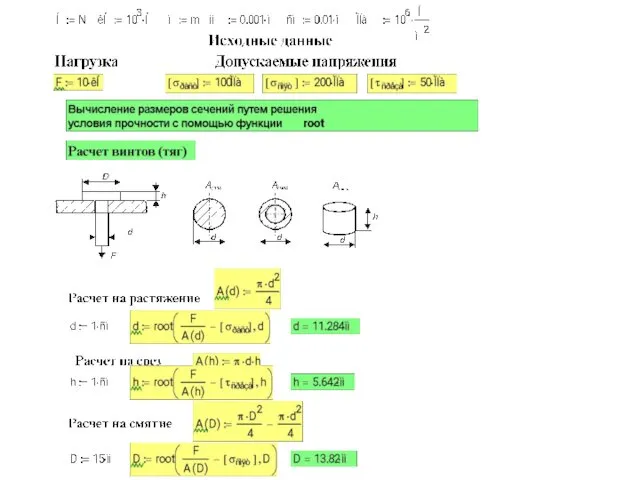
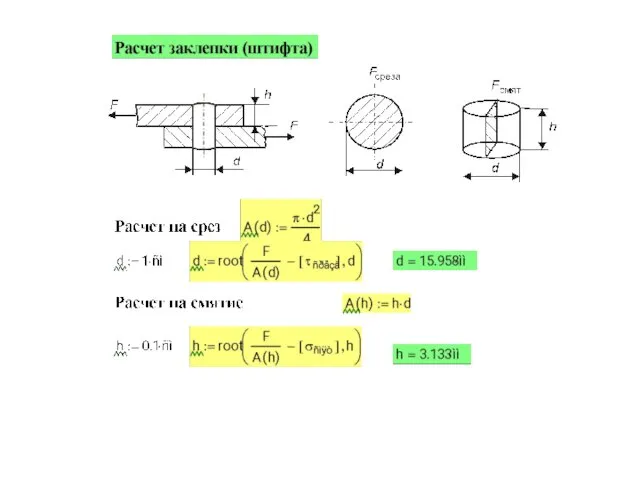
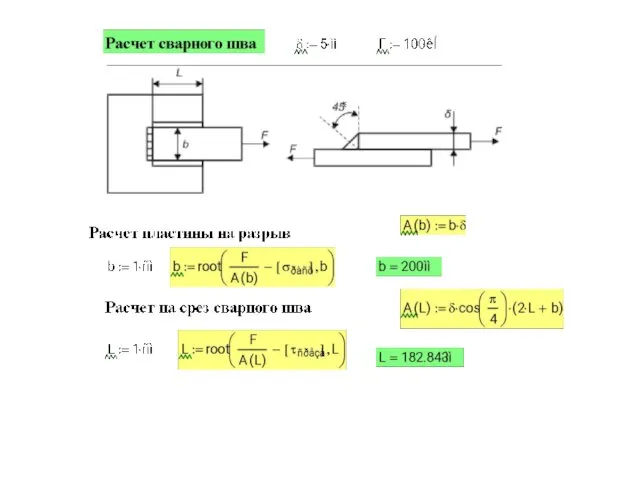
- 4. 2. Расчеты соединений, работающих на сдвиг Заклепочные соединения На рис. показана работа одиночной заклепки, соединяющей три
- 5. Помимо среза при относительно тонких листах возможно нарушение соединения вследствие смятия листов или заклепки по поверхности
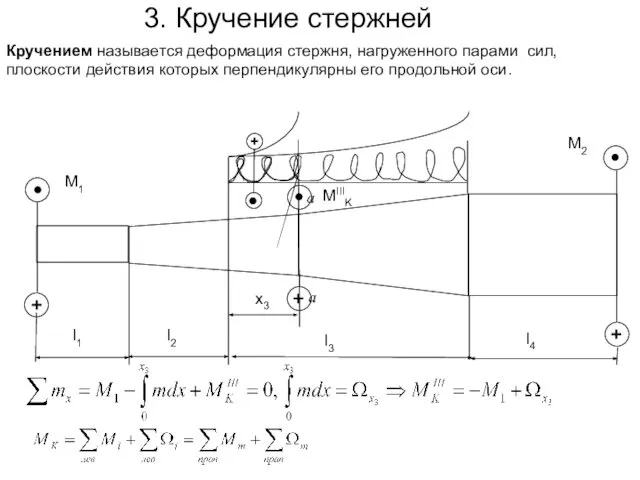
- 10. Кручением называется деформация стержня, нагруженного парами сил, плоскости действия которых перпендикулярны его продольной оси. M1 M2
- 11. Принимаем предположения, которые подтверждаются решением задами о кручении методами теории упругости: При кручении стержней кольцевого сечения
- 12. Максимальное касательное напряжение в сечении любой формы при кручении всегда определяется по формуле где WK -
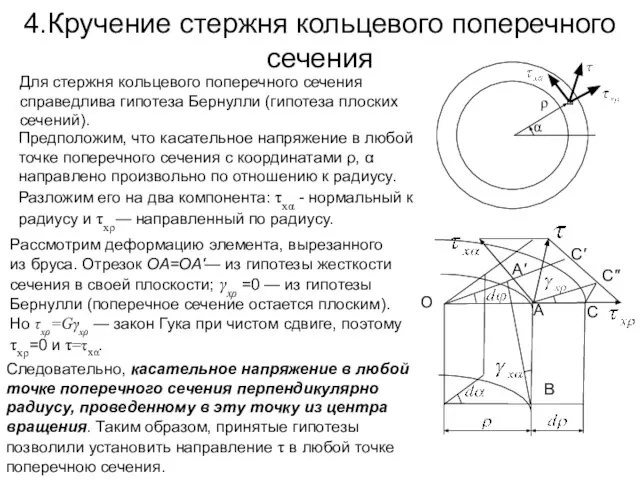
- 13. 4.Кручение стержня кольцевого поперечного сечения α ρ Для стержня кольцевого поперечного сечения справедлива гипотеза Бернулли (гипотеза
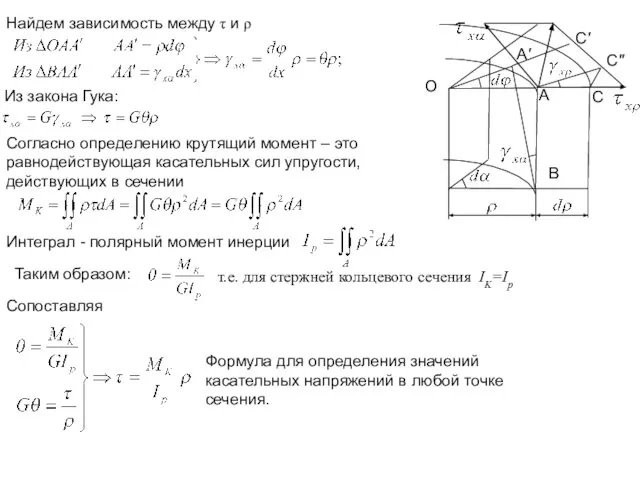
- 14. Интеграл - полярный момент инерции Найдем зависимость между τ и ρ Из закона Гука: Согласно определению
- 15. Касательные напряжения в поперечном сечении изменяются вдоль радиуса по линейному закону, достигая максимума в точках наружного
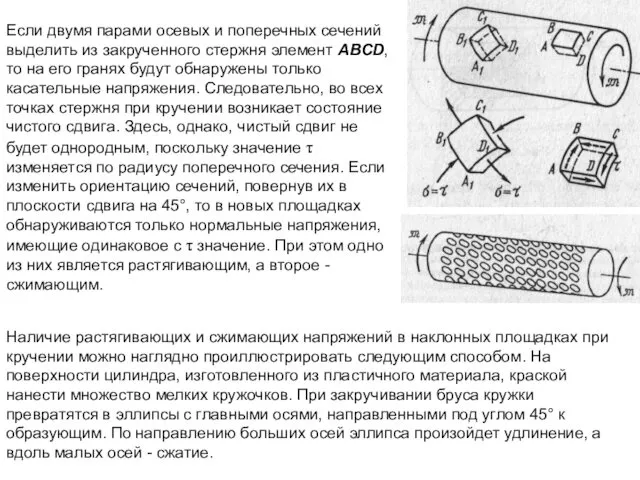
- 16. Если двумя парами осевых и поперечных сечений выделить из закрученного стержня элемент ABCD, то на его
- 17. Потенциальная энергия деформации при кручении Mк dx Внешние силы, создающие упругую деформацию стержня, совершают некоторую работу,
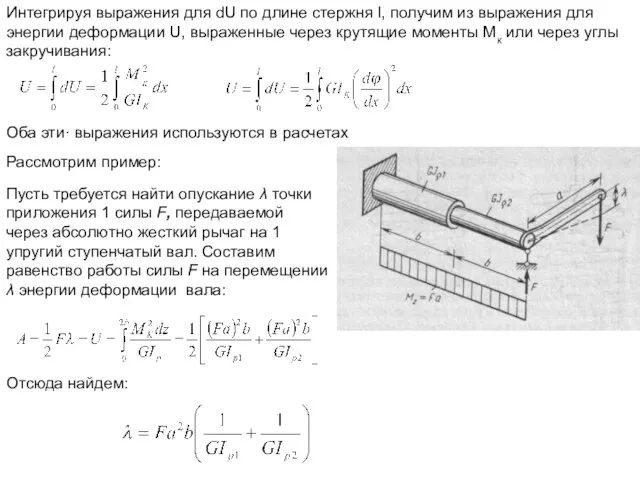
- 18. Интегрируя выражения для dU по длине стержня l, получим из выражения для энергии деформации U, выраженные
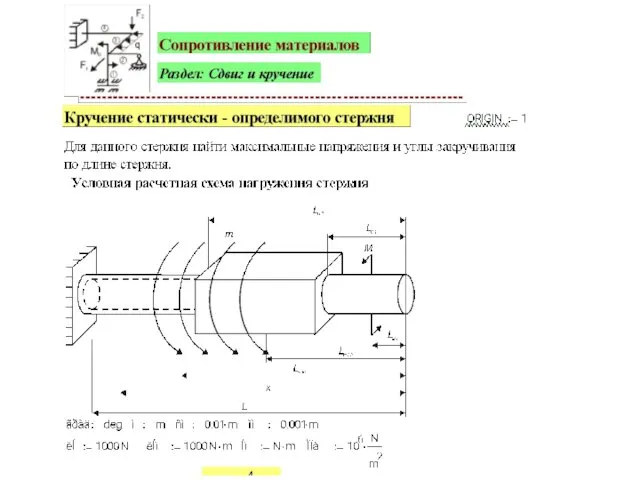
- 19. 5. Результаты механических испытаний при кручении, расчеты на прочность и жесткость Механические испытания на кручение проводят
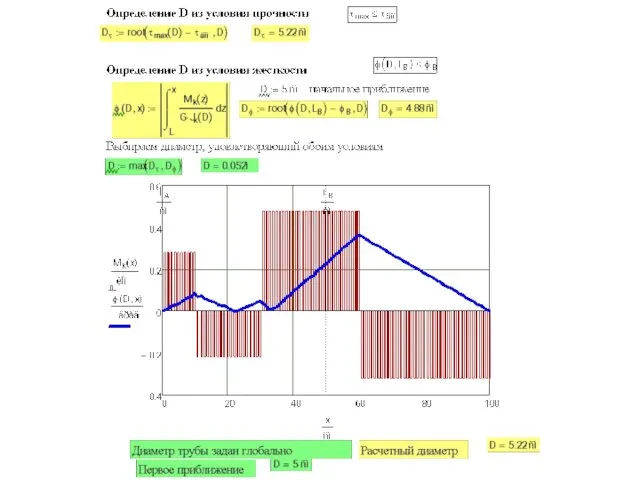
- 20. Расчеты на прочность и жесткость при кручении Расчет на прочность Условие прочности проектировочного расчета Условие прочности
- 21. Расчет на жесткость Условие жесткости θ – в радианах/метр θ – в градусах/метр Допускаемый погонный угол
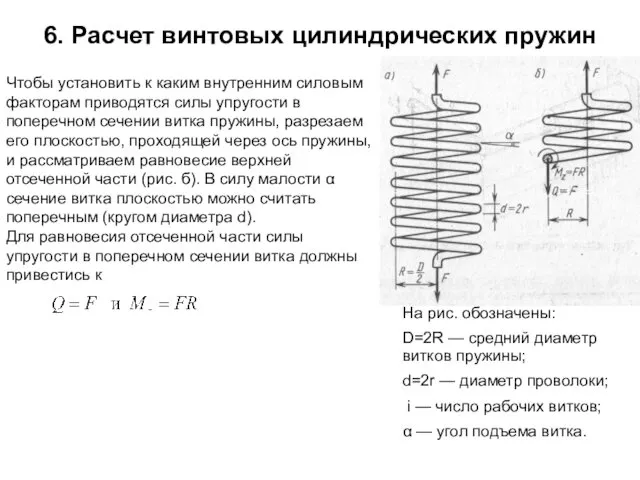
- 22. 6. Расчет винтовых цилиндрических пружин Чтобы установить к каким внутренним силовым факторам приводятся силы упругости в
- 23. Распределение касательных напряжений по поперечному сечению oт Qy и Мк показаны на рис. Опасной будет точка
- 24. Важной характеристикой упругих свойств пружины является жесткость пружины с — так называется сила F, которая вызывает
- 25. 7. Кручение стержней с некруглым поперечным сечением. Мембранная аналогия. Определение напряжений в стержне с некруглым поперечным
- 26. Рассмотрим общие положения относительно законов распределения напряжений в поперечных сечениях некруглой формы, а затем приведем готовые
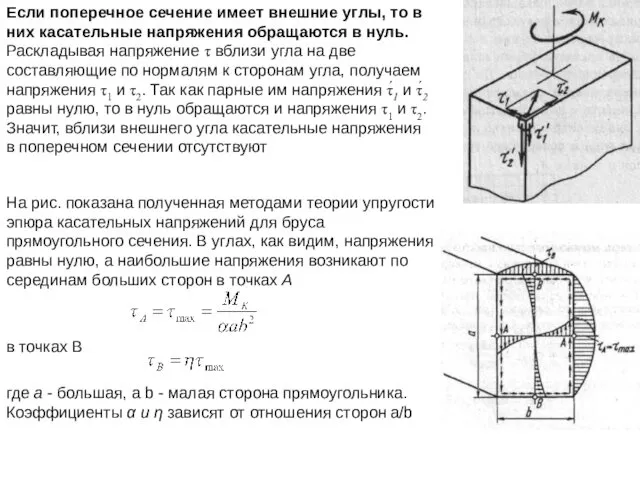
- 27. Если поперечное сечение имеет внешние углы, то в них касательные напряжения обращаются в нуль. Раскладывая напряжение
- 28. Таблица 2.1. Значения коэффициентов α, β и η Значения коэффициентов α, β и η Угловое перемещение
- 29. Угловое перемещение для стержня эллиптического сечения имеет следующее выражение: Для сечения, имеющего форму равностороннего треугольника со
- 30. Краткие сведения о пленочной (мембранной) аналогии В результате того, что аналитическое решение задачи о кручении стержня
- 31. Характер деформации пленки под действием давления можно всегда представить себе, если не точно, то, во всяком
- 40. 8. Кручение тонкостенного стержня В практике машиностроения, и особенно самолетостроения, часто возникает необходимость расчета на кручение
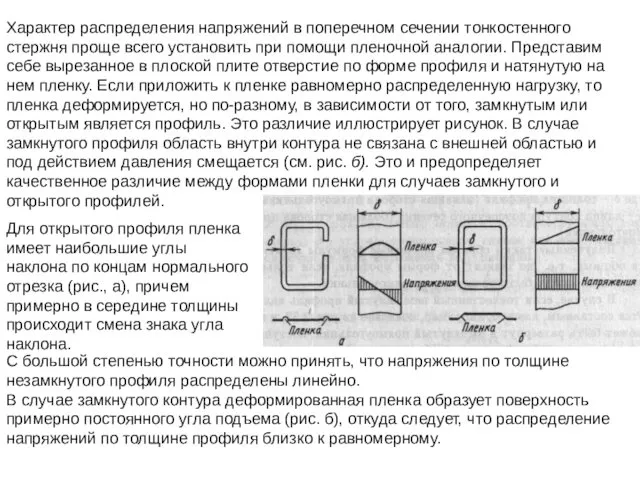
- 41. Характер распределения напряжений в поперечном сечении тонкостенного стержня проще всего установить при помощи пленочной аналогии. Представим
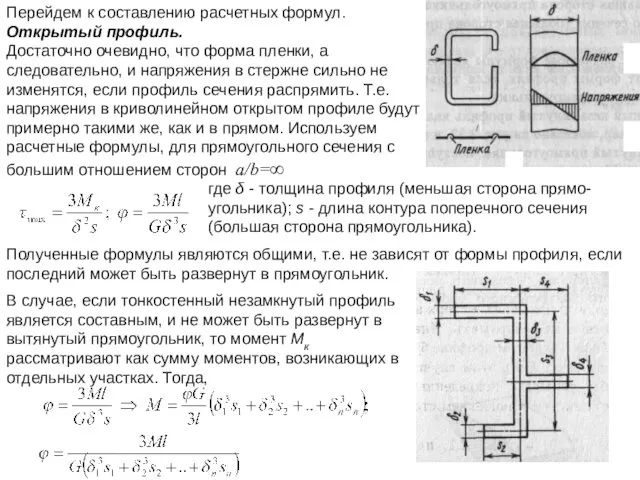
- 42. Перейдем к составлению расчетных формул. Открытый профиль. Достаточно очевидно, что форма пленки, а следовательно, и напряжения
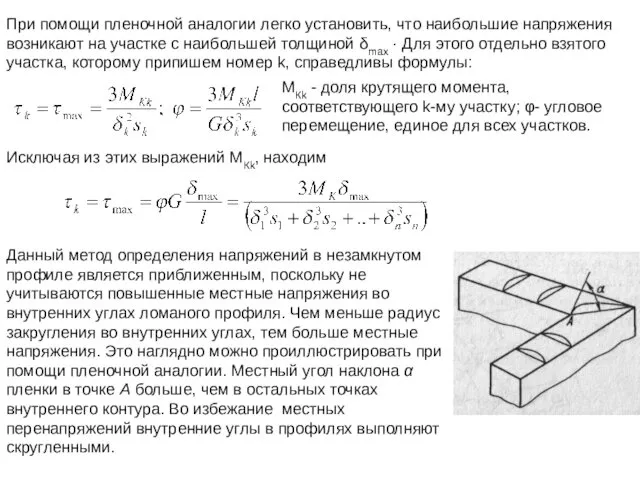
- 43. При помощи пленочной аналогии легко установить, что наибольшие напряжения возникают на участке с наибольшей толщиной δmах
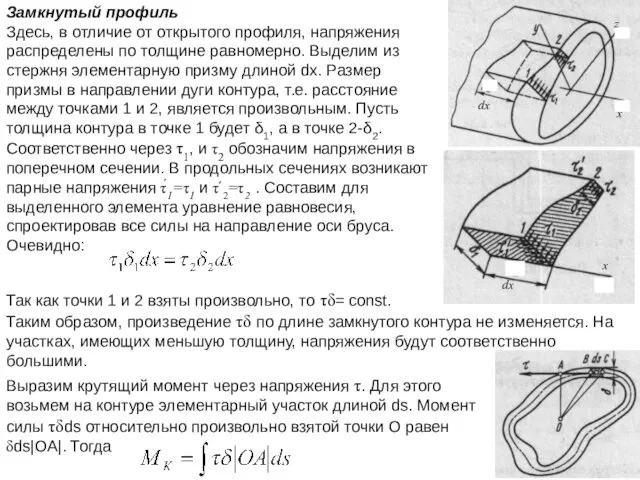
- 44. Замкнутый профиль Здесь, в отличие от открытого профиля, напряжения распределены по толщине равномерно. Выделим из стержня
- 45. Произведение τδ по длине дуги контура не изменяется Произведение \OA\ds представляет собой удвоенную площадь треугольника ОВС,
- 46. Энергия, накопленная в элементарном объеме с размерами ds, dx, δ, равна Это выражение должно быть проинтегрировано
- 48. Скачать презентацию
























 Плоский изгиб. Деформации и перемещения балки
Плоский изгиб. Деформации и перемещения балки Закон Ома для участка цепи Презентация
Закон Ома для участка цепи Презентация ЭПРА люминесцентных ламп
ЭПРА люминесцентных ламп Ультразвук. Источники и применение
Ультразвук. Источники и применение Интерференция света. (Лекция 11)
Интерференция света. (Лекция 11) Ачыкларга
Ачыкларга Курс лекций. Электрический привод
Курс лекций. Электрический привод Испытания, эксплуатация, техническое обслуживание металлорежущего оборудования
Испытания, эксплуатация, техническое обслуживание металлорежущего оборудования Решение задач
Решение задач Подготовка к ЕГЭ. Фотоэффект
Подготовка к ЕГЭ. Фотоэффект Тушение люминесценции
Тушение люминесценции Электричество и магнетизм
Электричество и магнетизм Червячные передачи (ЧП) (продолжение)
Червячные передачи (ЧП) (продолжение) Сила Трения Презентацию подготовили: Учащиеся 9 класса: Щурихин Владислав Волкова Юлия Руководитель проекта: Сивир
Сила Трения Презентацию подготовили: Учащиеся 9 класса: Щурихин Владислав Волкова Юлия Руководитель проекта: Сивир Презентация по физике "Лауреаты Нобелевской премии по физике" - скачать
Презентация по физике "Лауреаты Нобелевской премии по физике" - скачать  Регулирование частоты тока авиационных генераторов. (Тема 3)
Регулирование частоты тока авиационных генераторов. (Тема 3) Дефекты структуры кристаллов
Дефекты структуры кристаллов Сопротивление потоку
Сопротивление потоку Аттестационная работа. Программа элективного курса по физике для 10-11 класса «Решение нестандартных задач по физике»
Аттестационная работа. Программа элективного курса по физике для 10-11 класса «Решение нестандартных задач по физике» Счастливый случай. Урок-игра по физике в 9 классе
Счастливый случай. Урок-игра по физике в 9 классе Закон Ома. Расчёт сопротивления проводника. (8 класс)
Закон Ома. Расчёт сопротивления проводника. (8 класс) Ультразвук. Джерела ультразвуку
Ультразвук. Джерела ультразвуку Рентгеновское излучение
Рентгеновское излучение Циклы
Циклы Механическая работа. Связь между работой и скоростью движения тела
Механическая работа. Связь между работой и скоростью движения тела Диффузионное приближение
Диффузионное приближение Энергия светового поля. Поток энергии в световой волне. Интенсивность света
Энергия светового поля. Поток энергии в световой волне. Интенсивность света Презентация по физике Магнитное поле земли
Презентация по физике Магнитное поле земли