Содержание
- 2. тогда по теореме о проекциях скоростей Пусть точка В1 движется со скоростью § 12. Некоторые виды
- 3. следовательно, Сложим эти выражения, воспользовавшись свойством внутренних сил, тогда имеем и теорема об изменении кинетической энергии
- 4. 12.2. Система с идеальными связями Рассмотрим систему, на которую наложены связи, не изменяющиеся со временем Разделим
- 5. 12.3. Примеры идеальных связей 1. Движение по гладкой поверхности 3. Качение без скольжения по твердой поверхности
- 6. 5. При нерастяжимых нитях и стержнях 6. Шарнирно неподвижная опора , если Fтр = 0 В
- 7. 1. Если тело двигается поступательно, то дифференциальное уравнение его движения запишется как движение центра масс §
- 8. (25) 3. Если тело двигается плоско-параллельно, то положение его центра масс описывает уравнение движения центра масс
- 9. § 14. Принцип Даламбера для механической системы Если в любой момент времени к каждой из точек
- 10. Введем обозначения − главный вектор сил инерции, Так как − условия равновесия механической системы − главный
- 11. 14.1. Главный вектор и главный момент сил инерции системы При поступательном движении (28) ? Главный вектор
- 12. По теореме об изменении кинетического момента − главный момент сил инерции системы относительно центра О (29)
- 13. 14.2. Приведение сил инерции твердого тела 1. Пусть механическая система движется поступательно, тогда Все силы инерции
- 14. здесь ε − угловое ускорение системы
- 15. 3. Вращение вокруг оси, проходящей через центр масс системы 4. Плоско-параллельное движение Если тело имеет плоскость
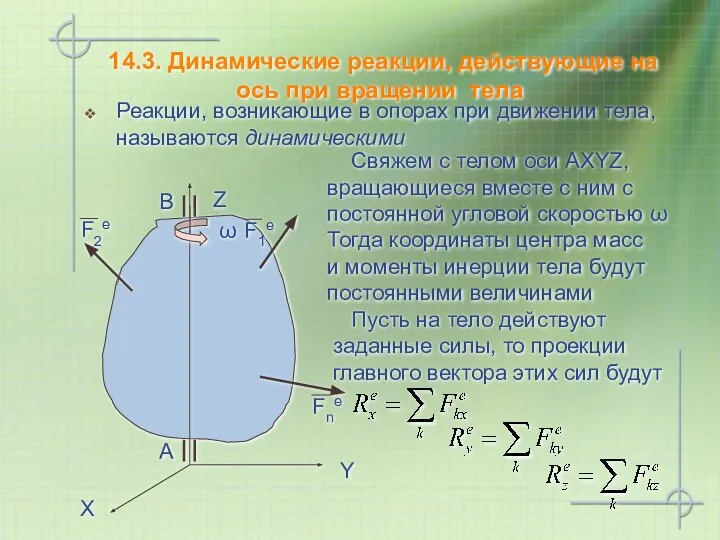
- 16. Свяжем с телом оси АХYZ, вращающиеся вместе с ним с постоянной угловой скоростью ω 14.3. Динамические
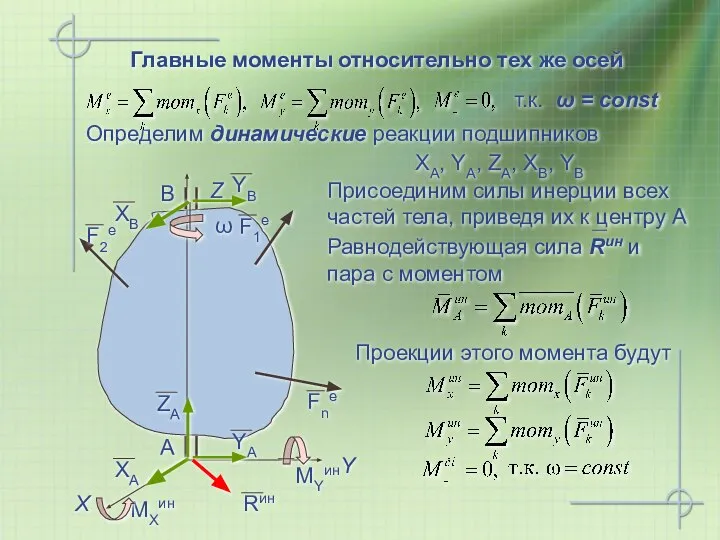
- 17. т.к. ω = const Главные моменты относительно тех же осей Определим динамические реакции подшипников XA, YA,
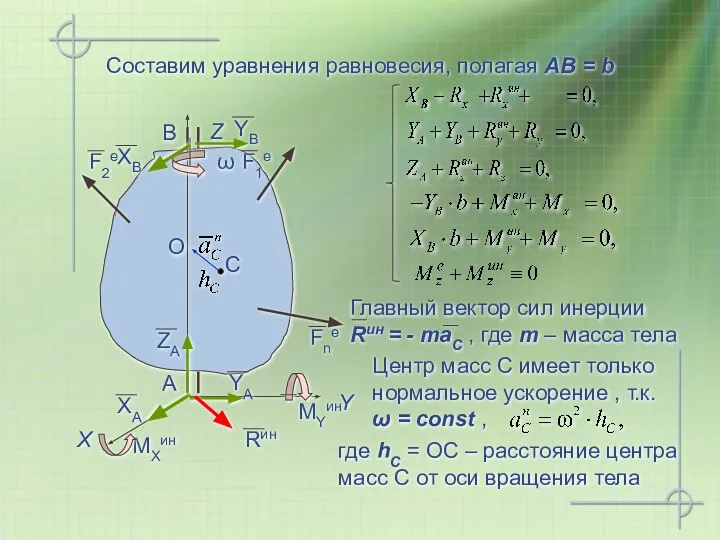
- 18. где hC = ОС – расстояние центра масс С от оси вращения тела Составим уравнения равновесия,
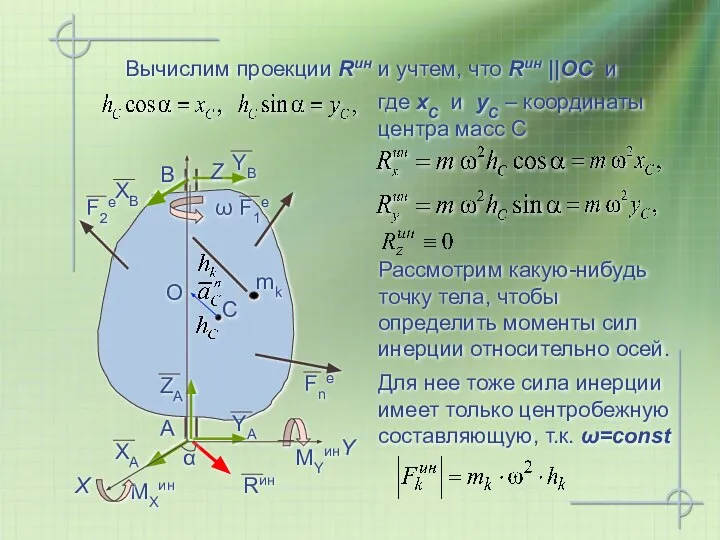
- 19. где xC и yC – координаты центра масс С Вычислим проекции Rин и учтем, что Rин
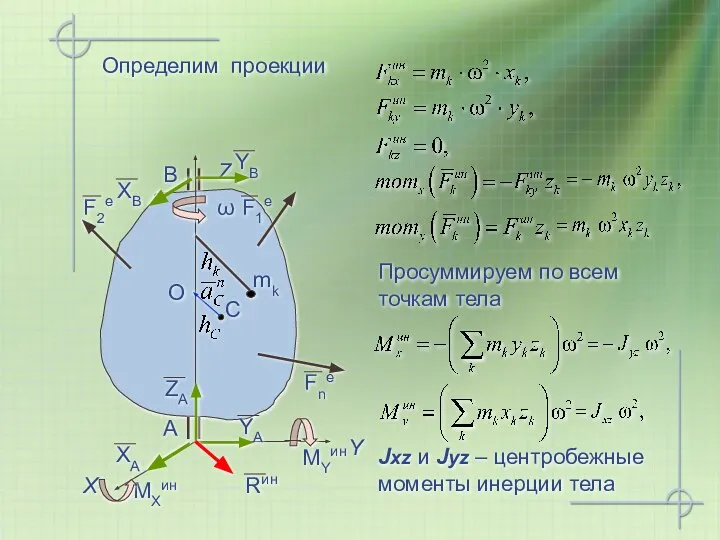
- 20. Определим проекции Просуммируем по всем точкам тела О Jxz и Jyz – центробежные моменты инерции тела
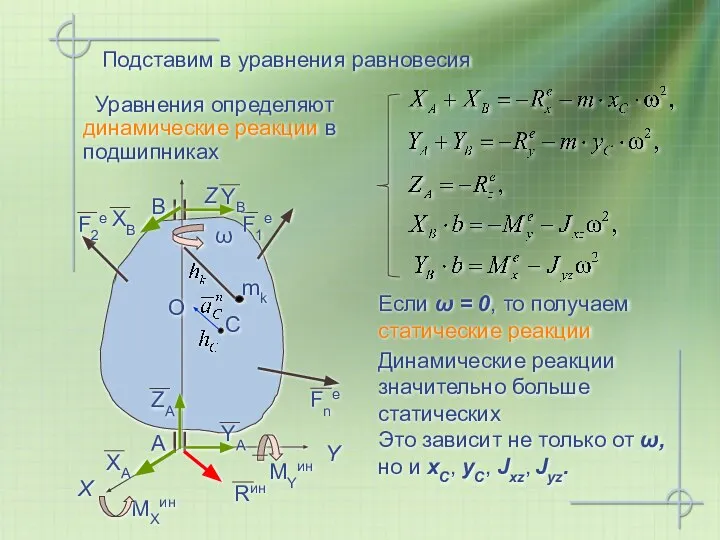
- 21. Динамические реакции значительно больше статических Подставим в уравнения равновесия Уравнения определяют динамические реакции в подшипниках О
- 22. Если хС = 0, yС = 0, Jxz = 0, Jyz = 0, то наличие вращения
- 23. Тогда х’С = 0, y’С = 0, J’xz= 0, J’yz = 0 Прибавим к телу ещё
- 25. Скачать презентацию
















 Определения и формулы наизусть, вопросы устно, упражнения письменно
Определения и формулы наизусть, вопросы устно, упражнения письменно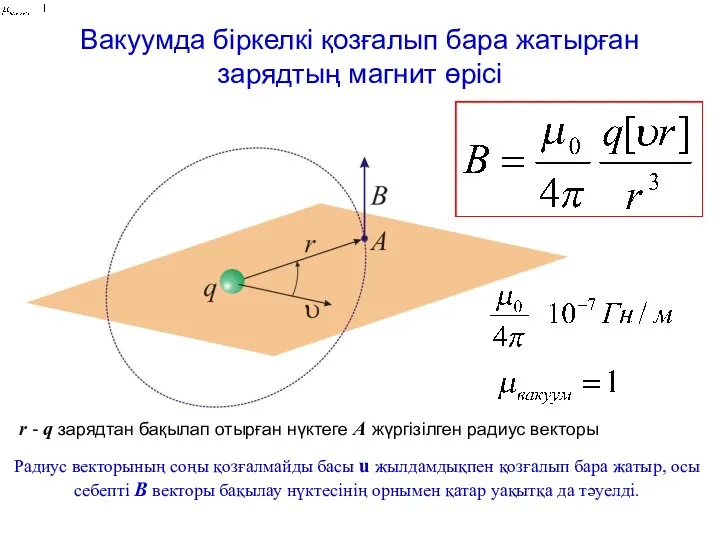 Вакуумда біркелкі қозғалып бара жатырған зарядтың магнит өрісі. (Лекция 12)
Вакуумда біркелкі қозғалып бара жатырған зарядтың магнит өрісі. (Лекция 12) Деревянные балки. лекция № 0
Деревянные балки. лекция № 0 Первый закон термодинамики
Первый закон термодинамики Геометрическая оптика. Радуга
Геометрическая оптика. Радуга Нанотехнологии
Нанотехнологии Всё живое из яйца. Исследовательская работа
Всё живое из яйца. Исследовательская работа Ультрафиолетовые лучи
Ультрафиолетовые лучи Электрический ток в вакууме
Электрический ток в вакууме Рентгеновское излучение, радиоактивность. Взаимодействие ионизирующего излучения с веществом. Дозиметрия ионизирующего излучен
Рентгеновское излучение, радиоактивность. Взаимодействие ионизирующего излучения с веществом. Дозиметрия ионизирующего излучен Модуляция света
Модуляция света Магнитное поле, его характеритики, виды
Магнитное поле, его характеритики, виды Элементы квантовой статистики. (Лекция 8)
Элементы квантовой статистики. (Лекция 8) Расчет электрических цепей постоянного тока, не содержащих источников ЭДС
Расчет электрических цепей постоянного тока, не содержащих источников ЭДС Показатели регулирования САУ
Показатели регулирования САУ Характеристика нейтронов
Характеристика нейтронов Медиаобразование, как средство активизации познавательной деятельности учащихся
Медиаобразование, как средство активизации познавательной деятельности учащихся Презентация по физике "Електромагнітні коливання. Резонанс. Автоколивання" - скачать бесплатно
Презентация по физике "Електромагнітні коливання. Резонанс. Автоколивання" - скачать бесплатно Механические свойства твердых тел. Механические колебания. Звук и ультразвук
Механические свойства твердых тел. Механические колебания. Звук и ультразвук Нелинейная физика. Турбулентность. Солитоны. Хаос. Странные аттракторы
Нелинейная физика. Турбулентность. Солитоны. Хаос. Странные аттракторы Long-period oscillations of sunspots and small-scale magnetic structures
Long-period oscillations of sunspots and small-scale magnetic structures Тепловые двигатели
Тепловые двигатели Презентация по физике Потенциал
Презентация по физике Потенциал  Измерение размеров малых тел. Лабораторная работа № 2
Измерение размеров малых тел. Лабораторная работа № 2 Положение об отделе главного механика
Положение об отделе главного механика Отражение звука. Эхо. Звуковой резонанс
Отражение звука. Эхо. Звуковой резонанс Векторлар өрісінің циркуляциясы, роторы
Векторлар өрісінің циркуляциясы, роторы Действие на растения радиации
Действие на растения радиации