Содержание
- 2. Дискретное преобразование Фурье Мысленно периодизируем этот сигнал с периодом Дискретный периодический сигнал можно представить рядом Фурье:
- 3. Дискретное преобразование Фурье Переходя к новой переменной , получим: Так как , окончательно имеем: (11.1)
- 4. Дискретное преобразование Фурье Соотношение, позволяющее вычислить комплексные амплитуды гармоник дискретного сигнала, представляет собой линейную комбинацию отсчетов
- 5. Свойства дискретного преобразования Фурье Линейность. Дискретное преобразование Фурье – линейное преобразование, то есть если последовательностям и
- 6. Свойства дискретного преобразования Фурье Симметрия. Свойство симметрии, которым обладает спектр непрерывного сигнала, сохраняется и для спектра
- 7. Свойства дискретного преобразования Фурье Гармоника с нулевым номером (постоянная составляющая) представляет собой среднее значение всех отсчетов
- 8. Свойства дискретного преобразования Фурье ДПФ круговой свертки. Возьмем две последовательности и одинаковой длины , ДПФ которых
- 9. Свойства дискретного преобразования Фурье Таким образом, круговой свертке дискретизированных и заданных на одном временном промежутке сигналов
- 10. Свойства дискретного преобразования Фурье Равенство Парсеваля для дискретных сигналов. Определим значение , используя формулу ДПФ: Таким
- 12. Скачать презентацию









 Напомним: Энергия системы Полная энергия системы складывается из кинетической энергии системы Ек (если скорость центра масс с
Напомним: Энергия системы Полная энергия системы складывается из кинетической энергии системы Ек (если скорость центра масс с Молекулярная физика
Молекулярная физика Твердые тела и их свойства
Твердые тела и их свойства Ядерный (атомный) реактор
Ядерный (атомный) реактор Линза. Построение изображения в линзе. Формула тонкой линзы
Линза. Построение изображения в линзе. Формула тонкой линзы Электрические машины. Тема1. Конструкция машин постоянного тока (МПТ)
Электрические машины. Тема1. Конструкция машин постоянного тока (МПТ) Скорость и ускорение материальной точки
Скорость и ускорение материальной точки Настройка трансмиссии
Настройка трансмиссии Инерция Урок физики в 7 классе
Инерция Урок физики в 7 классе 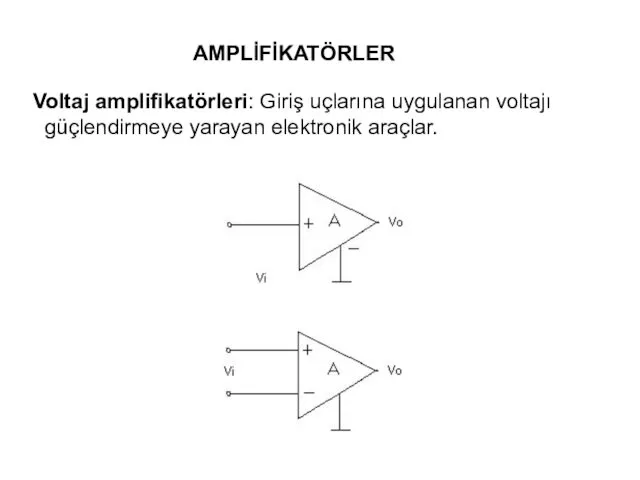 Ampli̇fi̇katörler. Voltaj amplifikatörleri: giriş uçlarına uygulanan voltajı güçlendirmeye yarayan elektronik araçlar
Ampli̇fi̇katörler. Voltaj amplifikatörleri: giriş uçlarına uygulanan voltajı güçlendirmeye yarayan elektronik araçlar Преобразование пассивной звезды в треугольник
Преобразование пассивной звезды в треугольник Решение задач по теме «Соединение проводников»
Решение задач по теме «Соединение проводников»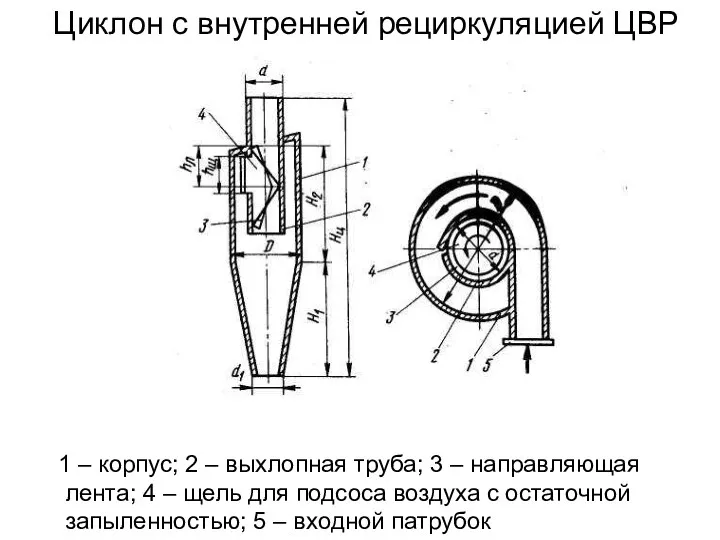 Циклон с внутренней рециркуляцией ЦВР
Циклон с внутренней рециркуляцией ЦВР На железной дороге
На железной дороге Деформація
Деформація Решение задач по теме Прямолинейное равноускоренное движение
Решение задач по теме Прямолинейное равноускоренное движение Конвекция. Ламинарный тепловой погранслой при вынужденном движении жидкости вдоль плоской поверхности. (Тема 2. Лекции 8,9)
Конвекция. Ламинарный тепловой погранслой при вынужденном движении жидкости вдоль плоской поверхности. (Тема 2. Лекции 8,9) Презентация по физике "Свойства постоянных магнитов" - скачать
Презентация по физике "Свойства постоянных магнитов" - скачать  Кинематика материальной точки и твердого тела
Кинематика материальной точки и твердого тела Теплоотдача при поперечном обтекании труб
Теплоотдача при поперечном обтекании труб Презентация по физике "Інфрачервоне випромінювання" - скачать бесплатно
Презентация по физике "Інфрачервоне випромінювання" - скачать бесплатно Механизмы уширения линий. Теория излучения. (Тема 12)
Механизмы уширения линий. Теория излучения. (Тема 12) Электрические цепи переменного тока
Электрические цепи переменного тока Элементы квантовой механики
Элементы квантовой механики Энергияның дәстүрден тыс коздері. Күн энергиясы немесе гелиоэнергетика
Энергияның дәстүрден тыс коздері. Күн энергиясы немесе гелиоэнергетика Инновационный проект производства фуллеренов
Инновационный проект производства фуллеренов Полет в космос
Полет в космос Ядерные реакции
Ядерные реакции