Содержание
- 2. Это связано с высокой концентрацией электронов проводимости в металле, плотно заполняющих уровни в зоне проводимости. Каждый
- 3. Де Хааза - ван Альфена эффект ДЕ ХААЗА - ВАН АЛЬФЕНА ЭФФЕКТ - наблюдаемая в металлах
- 4. Энергия Ферми При Т=0 К Где - постоянная Планка, m – масса электрона, n – концентрация
- 5. Где - постоянная Планка, Т - температура k - постоянная Больцмана Энергия Ферми При Т 0
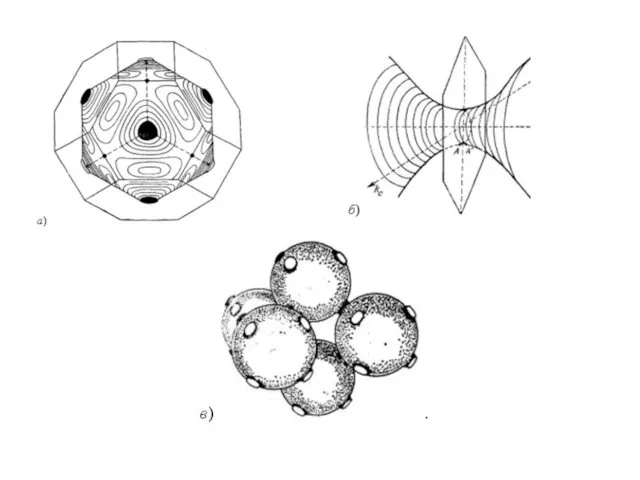
- 6. Продолжение. Поверхность Ферми. Если Ф. п. непрерывно проходит через всё пространство квазиимпульсов, она называется открытой. Если
- 7. Геометрические характеристики Ф. п. (форма, кривизна, площади сечений и т.п.) связаны с физическими свойствами металлов, что
- 8. Эффект Холла Эффектом Холла называется возникновение поперечного электрического поля и разности потенциалов в проводнике или полупроводнике,
- 9. Для большинства одноатомных металлов и многих интерметаллических соединений Ф. п. уже изучены. Теоретическое построение Ф. п.
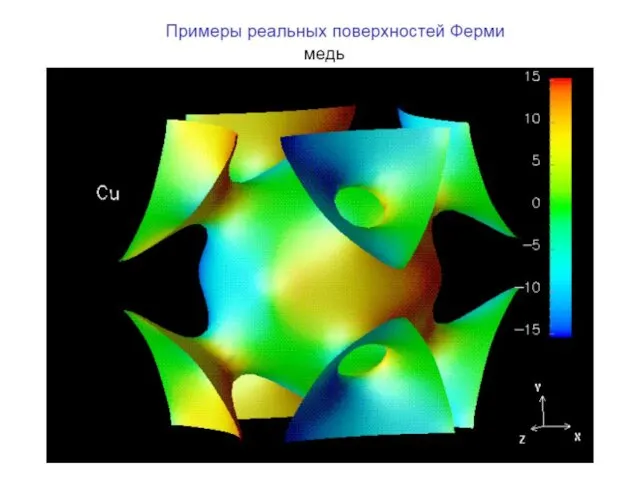
- 10. Примеры поверхности Ферми Топология поверхности Ферми для меди, серебра и золота приблизительно одинаковая и представляет собой
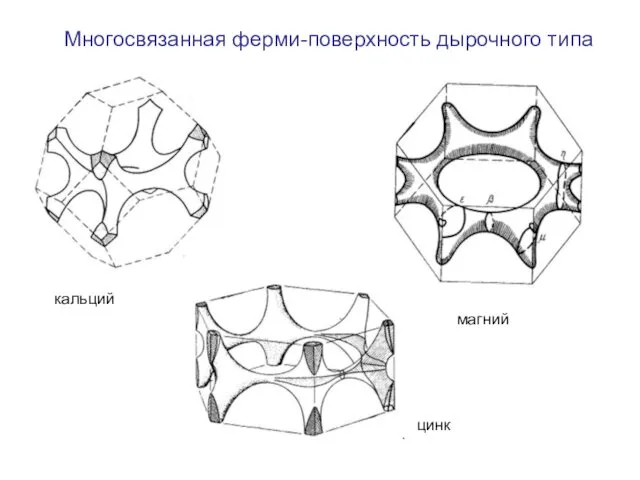
- 12. Многосвязанная ферми-поверхность дырочного типа кальций магний цинк
- 18. kF – импульс Ферми
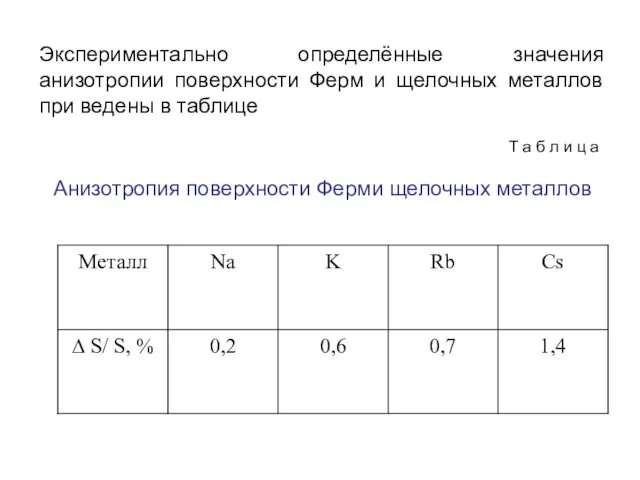
- 19. Небольшое отклонение поверхности Ферми от сферы количественно можно охарактеризовать величиной анизотропии поверхности где Smах и Smin-
- 20. Экспериментально определённые значения анизотропии поверхности Ферм и щелочных металлов при ведены в таблице Т а б
- 22. Скачать презентацию















 Линзы. Построение изображений в линзах
Линзы. Построение изображений в линзах Закон всемирного тяготения. Методика решения задач
Закон всемирного тяготения. Методика решения задач Определение размеров последней ступени турбины
Определение размеров последней ступени турбины Деформационные термометры
Деформационные термометры Огнестойкость строительных конструкций Член-корреспондент РААСН, доктор технических наук, профессор Фёдоров Виктор Сергееви
Огнестойкость строительных конструкций Член-корреспондент РААСН, доктор технических наук, профессор Фёдоров Виктор Сергееви Задача на расчет архимедовой силы
Задача на расчет архимедовой силы Преобразователи постоянного напряжения без потенциальной развязки
Преобразователи постоянного напряжения без потенциальной развязки Высокочастотный трансформатор Тесла (11 класс)
Высокочастотный трансформатор Тесла (11 класс) Материялық нүкте және қатты дене динамикасы. Механикадағы сақталу заңдары. Жұмыс және қуат
Материялық нүкте және қатты дене динамикасы. Механикадағы сақталу заңдары. Жұмыс және қуат Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Проводники и диэлектрики
Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Проводники и диэлектрики Механические колебания и волны. Звук
Механические колебания и волны. Звук Светодиоды и полупроводниковые лазеры
Светодиоды и полупроводниковые лазеры Condensatorul electric este un sistem
Condensatorul electric este un sistem Определение расстояния до недоступной точки
Определение расстояния до недоступной точки Измерение скорости света
Измерение скорости света Как работает паровой двигатель
Как работает паровой двигатель Зарождение физических методов неразрушающего контроля
Зарождение физических методов неразрушающего контроля Биополярные СВЧ-транзисторы
Биополярные СВЧ-транзисторы Резина и каучук
Резина и каучук Кинематика. Основные законы движения
Кинематика. Основные законы движения Асинхронные генераторы
Асинхронные генераторы Призначення, будова і принцип дії фотоелектроколоритра. Застосування в медицині
Призначення, будова і принцип дії фотоелектроколоритра. Застосування в медицині Люминесценция биологических объектов
Люминесценция биологических объектов Строение жидких, твердых и газообразных тел с точки зрения молекулярнокинетической теории
Строение жидких, твердых и газообразных тел с точки зрения молекулярнокинетической теории Электроёмкость. Конденсаторы
Электроёмкость. Конденсаторы Золотое правило механики
Золотое правило механики Давление. Единицы давления
Давление. Единицы давления §39-41. Электрическое напряжение. Вольтметр
§39-41. Электрическое напряжение. Вольтметр