Содержание
- 2. § 11. Особенности струйного течения Свободной турбулентной называется струя, распространяющаяся вдали от твердых поверхностей. Это один
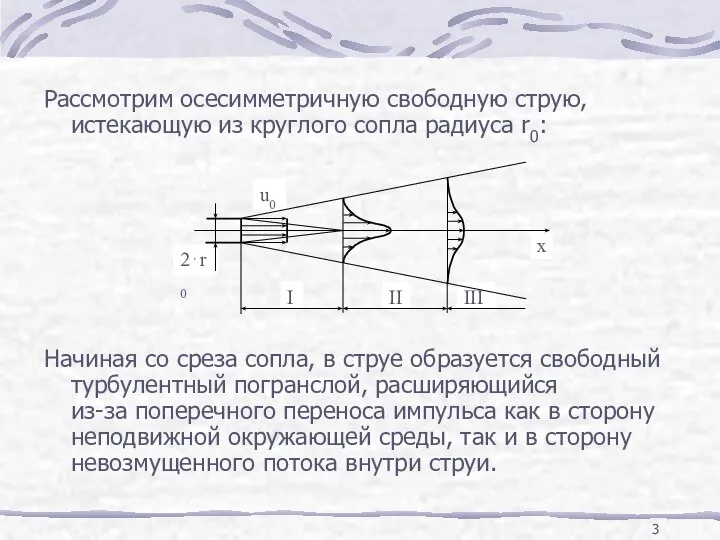
- 3. Рассмотрим осесимметричную свободную струю, истекающую из круглого сопла радиуса r0: Начиная со среза сопла, в струе
- 4. Начальным называется участок, на протяжении которого продолжает существовать невозмущенный поток внутри струи (I). На переходном участке
- 5. Экспериментально установленным фактом является прямолинейность границ свободных турбулентных струй: R = r0 + c ⋅ x
- 6. Воспользовавшись этими свойствами, найдем закон изменения скорости на оси основного участка струи um (x). Поток импульса
- 7. Вводя обозначение η=y/R и учитывая автомодельность поперечных профилей скорости, получим: . Интеграл в правой части этого
- 8. Приравняв последнее выражение к начальному потоку импульса , получим после сокращений и с учетом линейного нарастания
- 9. Объемный расход через поперечное сечение струи . Интеграл в правой части тоже является числом, которое обозначим
- 10. Рассчитаем изменение потока кинетической энергии по длине струи, то есть величину энергии, проходящей через все поперечное
- 12. Скачать презентацию








 Рух тіла під дією кількох сил. Розв’язування задач (урок 76)
Рух тіла під дією кількох сил. Розв’язування задач (урок 76) Силы Ампера и Лоренца
Силы Ампера и Лоренца Распределительное устройство 10 кВ
Распределительное устройство 10 кВ Векторы. Векторные величины
Векторы. Векторные величины Без имени-0318-0337-drwg_1(12) CH(ru)
Без имени-0318-0337-drwg_1(12) CH(ru) Нахождение удельной теплоты плавления льда в опытах по плавлению льда нагретыми металлическими цилиндрами
Нахождение удельной теплоты плавления льда в опытах по плавлению льда нагретыми металлическими цилиндрами История развития энергетики. Циклы этногенеза
История развития энергетики. Циклы этногенеза Ремонт воздухопровода и тормозной арматуры грузового вагона (с углублённой разработкой ремонта соединительных тормозных рукавов)
Ремонт воздухопровода и тормозной арматуры грузового вагона (с углублённой разработкой ремонта соединительных тормозных рукавов) Основы теории подобия
Основы теории подобия Мойка и очистка при ремонте машин
Мойка и очистка при ремонте машин Физика – наука, которая нужна
Физика – наука, которая нужна Механическое движение
Механическое движение Аттестационная работа. Образовательная программа внеурочной деятельности по физике Юный исследователь
Аттестационная работа. Образовательная программа внеурочной деятельности по физике Юный исследователь Ионизирующее излучение: термины, понятия, механизмы
Ионизирующее излучение: термины, понятия, механизмы Техпроцесс механообработки
Техпроцесс механообработки Общие понятия об эталонах
Общие понятия об эталонах Необслуживаемые аккумуляторные батареи
Необслуживаемые аккумуляторные батареи Домашнее задание. Механические колебания
Домашнее задание. Механические колебания Закон всемирного тяготения
Закон всемирного тяготения Термоядерные реакции
Термоядерные реакции Ядерные реакции
Ядерные реакции Звуковые волны
Звуковые волны Устройство, техническое обслуживание и ремонт пускового двигателя трактора беларус МТЗ – 82
Устройство, техническое обслуживание и ремонт пускового двигателя трактора беларус МТЗ – 82 Принципы полета
Принципы полета Биофизика дыхания. Объемы и емкости легких
Биофизика дыхания. Объемы и емкости легких Наземные телескопы
Наземные телескопы Применение радиоактивных изотопов
Применение радиоактивных изотопов Что такое гроза? Почему светит молния и гремит гром?
Что такое гроза? Почему светит молния и гремит гром?