Содержание
- 2. 1. Понятие механики, разделы в механике
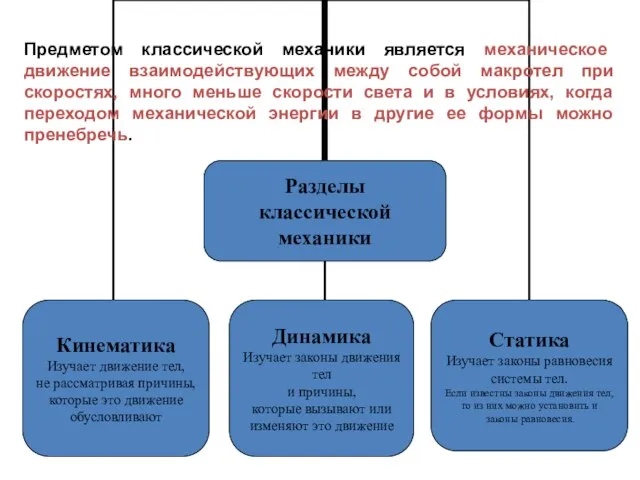
- 3. Предметом классической механики является механическое движение взаимодействующих между собой макротел при скоростях, много меньше скорости света
- 4. Модели в механике МАТЕРИАЛЬНАЯ ТОЧКА - тело, размерами и формой которого можно пренебречь в данной задаче.
- 5. 2.2. Система отсчета, тело отсчета Всякое движение относительно, поэтому для описания движения необходимо условиться, относительно какого
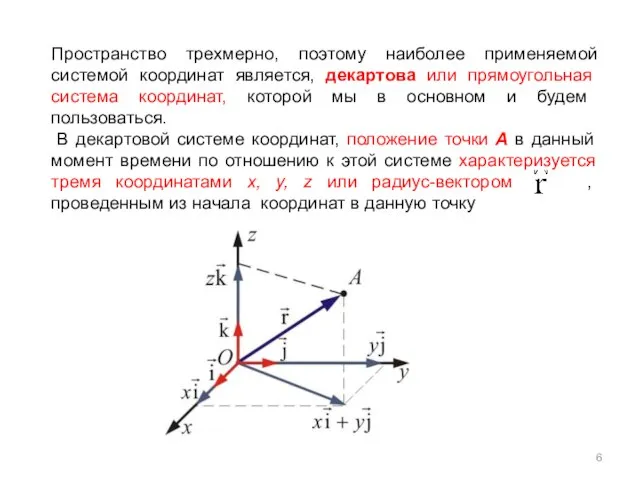
- 6. Пространство трехмерно, поэтому наиболее применяемой системой координат является, декартова или прямоугольная система координат, которой мы в
- 7. Кинематические уравнения движения материальной точки: Эти уравнения эквивалентны векторному уравнению где х, у, z – проекции
- 8. Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы i Если материальная
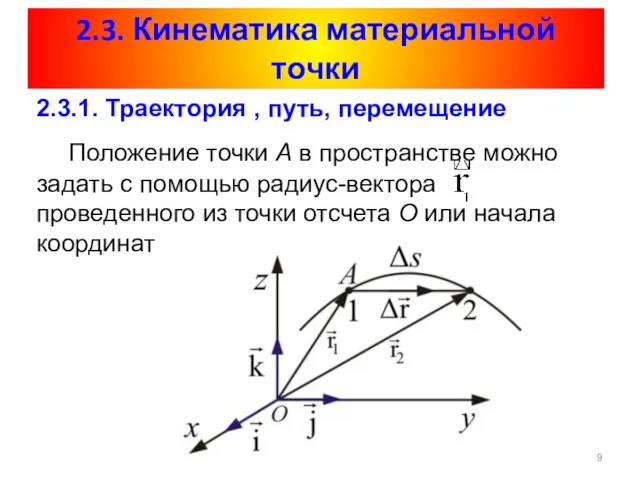
- 9. 2.3. Кинематика материальной точки 2.3.1. Траектория , путь, перемещение Положение точки А в пространстве можно задать
- 10. При движении точки А из точки 1 в точку 2 её радиус-вектор изменяется и по величине,
- 11. Пусть за время Δt точка А переместилась из точки 1 в точку 2. Вектор перемещения есть
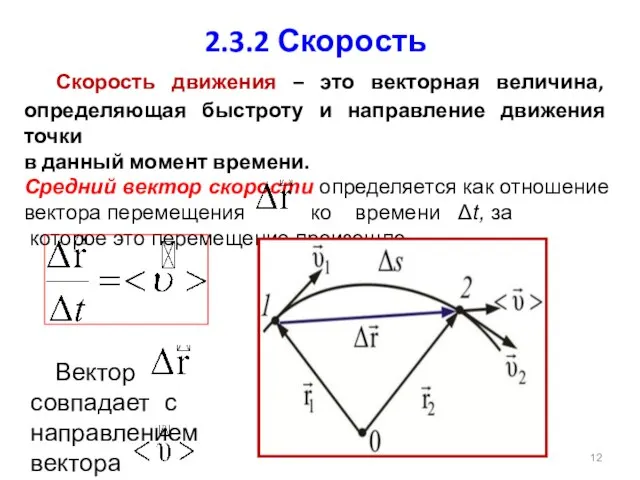
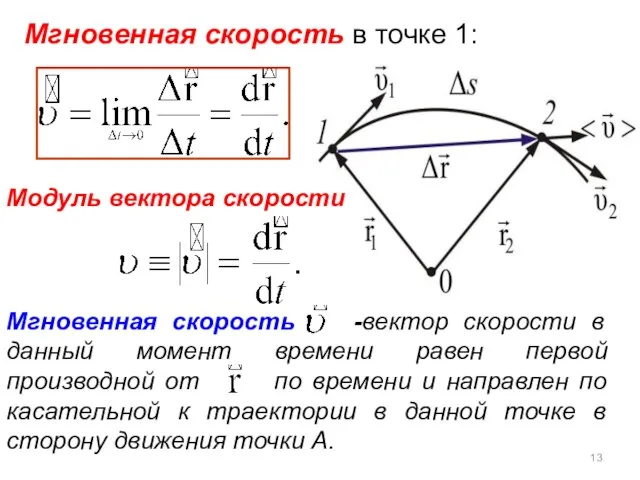
- 12. 2.3.2 Скорость Скорость движения – это векторная величина, определяющая быстроту и направление движения точки в данный
- 13. Мгновенная скорость -вектор скорости в данный момент времени равен первой производной от по времени и направлен
- 14. При Δt → 0 т.е. на бесконечно малом участке траектории (перемещение совпадает с траекторией) В этом
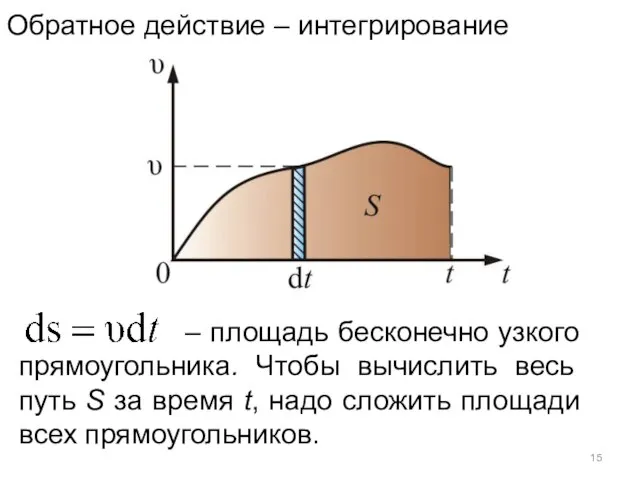
- 15. Обратное действие – интегрирование – площадь бесконечно узкого прямоугольника. Чтобы вычислить весь путь S за время
- 16. Геометрический смысл этого интеграла в том, что площадь под кривой есть путь тела за время t.
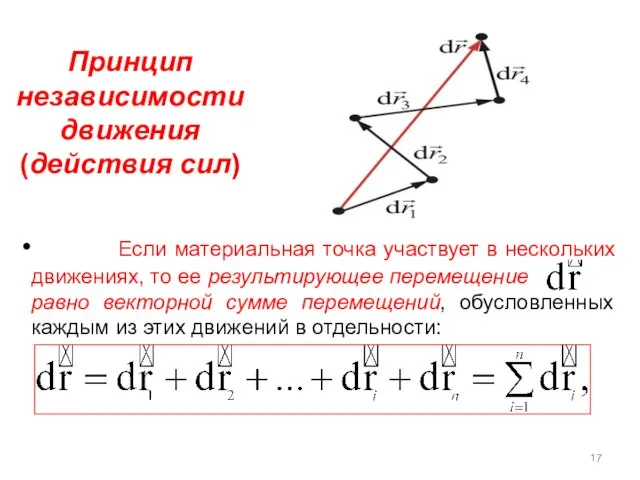
- 17. Если материальная точка участвует в нескольких движениях, то ее результирующее перемещение равно векторной сумме перемещений, обусловленных
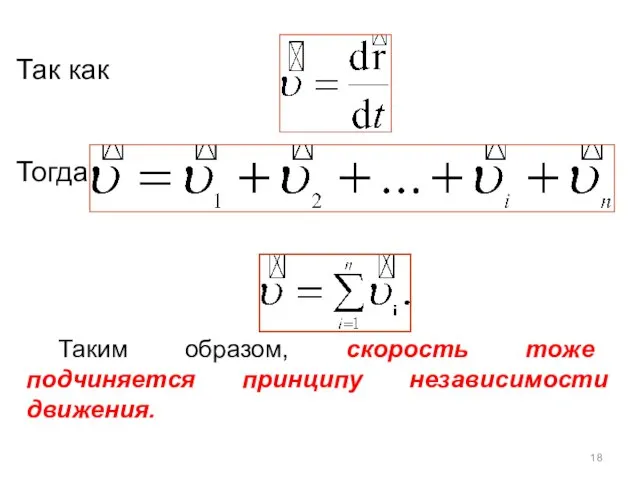
- 18. Так как Тогда Таким образом, скорость тоже подчиняется принципу независимости движения.
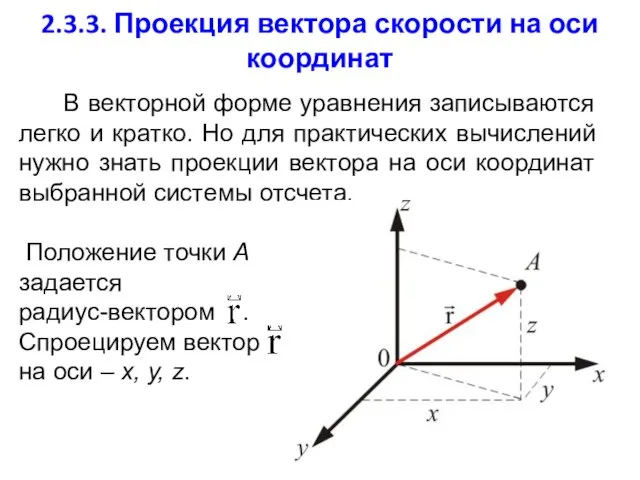
- 19. 2.3.3. Проекция вектора скорости на оси координат В векторной форме уравнения записываются легко и кратко. Но
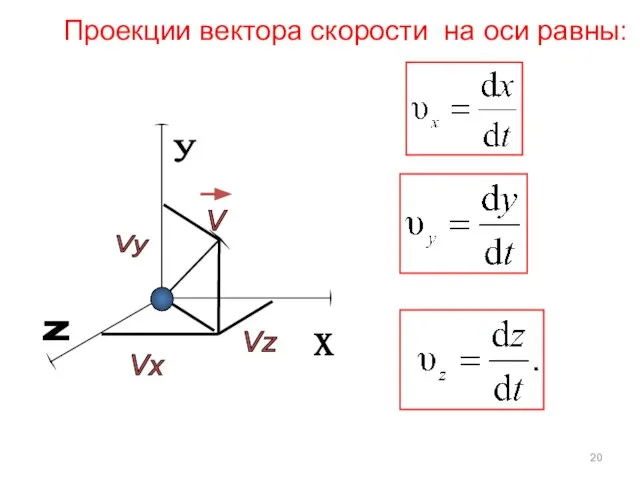
- 20. х у Z Проекции вектора скорости на оси равны:
- 21. где i, j, k единичные векторы – орты. Модуль вектора скорости: Так как вектор, то
- 22. Ускорение - это векторная величина, характеризующая быстроту изменения скорости по модулю и направлению. Единица измерения ускорения
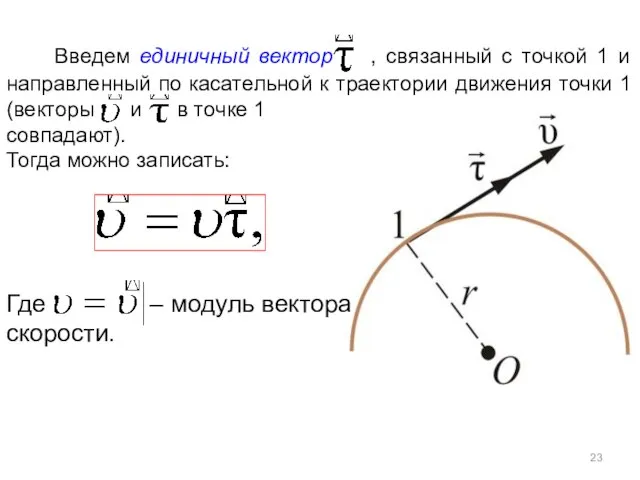
- 23. Введем единичный вектор , связанный с точкой 1 и направленный по касательной к траектории движения точки
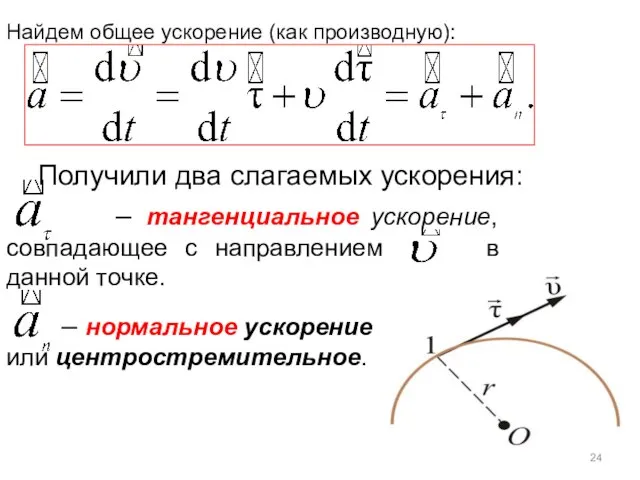
- 24. Найдем общее ускорение (как производную): Получили два слагаемых ускорения: – тангенциальное ускорение, совпадающее с направлением в
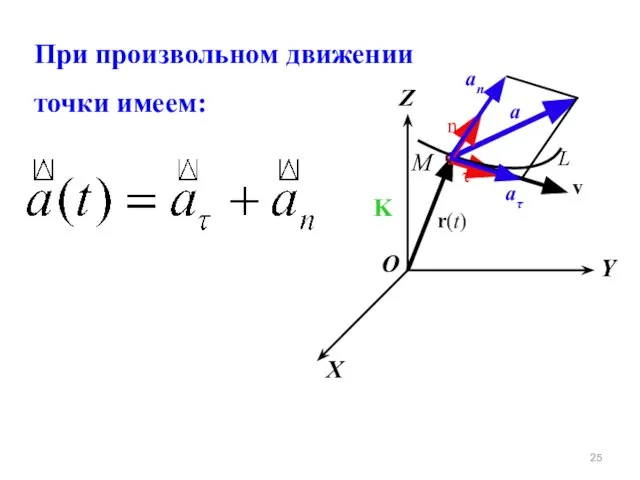
- 25. X Y Z K М r(t) L v a τ n При произвольном движении точки имеем:
- 26. или по модулю -показывает изменение вектора скорости по величине: - если то направлено в ту же
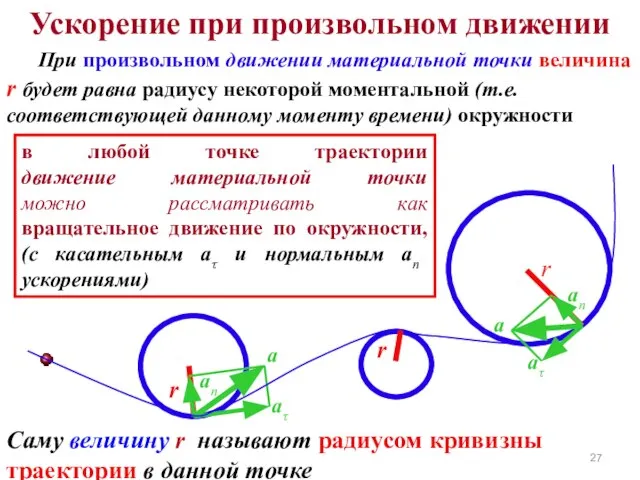
- 27. Ускорение при произвольном движении При произвольном движении материальной точки величина r будет равна радиусу некоторой моментальной
- 28. Центростремительным называют ускорение – когда движение происходит по окружности. А когда движение происходит по произвольной кривой
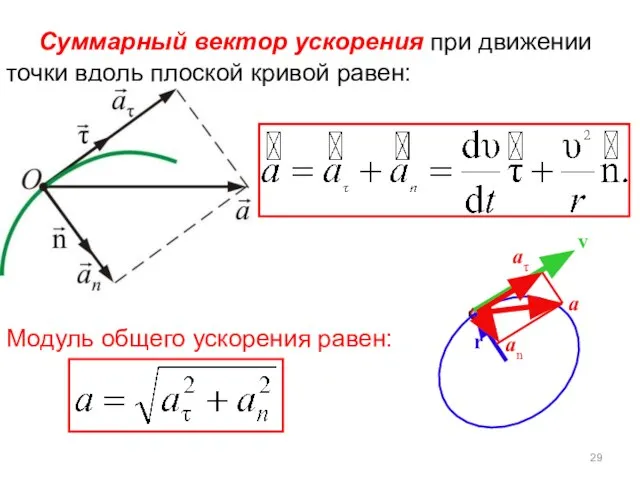
- 29. r v a an aτ Суммарный вектор ускорения при движении точки вдоль плоской кривой равен: Модуль
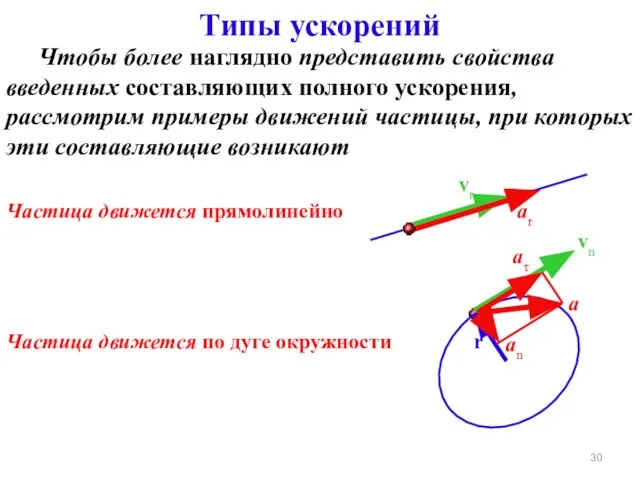
- 30. Типы ускорений Частица движется прямолинейно Чтобы более наглядно представить свойства введенных составляющих полного ускорения, рассмотрим примеры
- 31. При равномерном движении При движении с постоянным ускорением
- 32. 2.4. Кинематика твердого тела Различают пять видов движения твердого тела: - поступательное; - вращательное вокруг неподвижной
- 33. 2.4.1. Поступательное движение твердого тела Поступательное движение – это такое движение твердого тела, при котором любая
- 34. Скорости и ускорения всех точек твердого тела в данный момент времени t одинаковы. Это позволяет свести
- 35. При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той
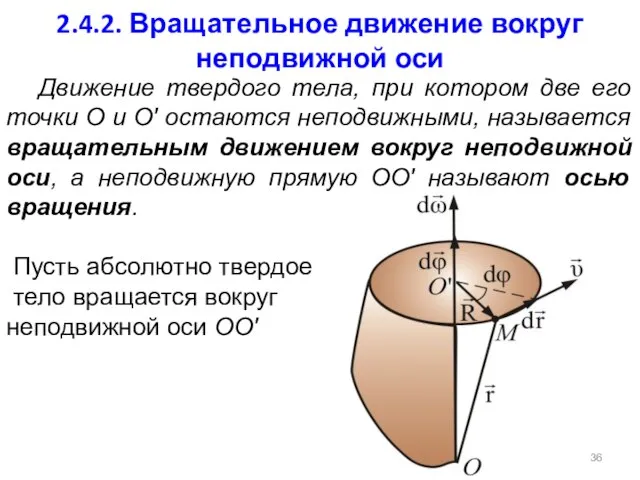
- 36. 2.4.2. Вращательное движение вокруг неподвижной оси Движение твердого тела, при котором две его точки О и
- 37. Угол поворота характеризует перемещения всего тела за время dt (угловой путь) Удобно ввести – вектор элементарного
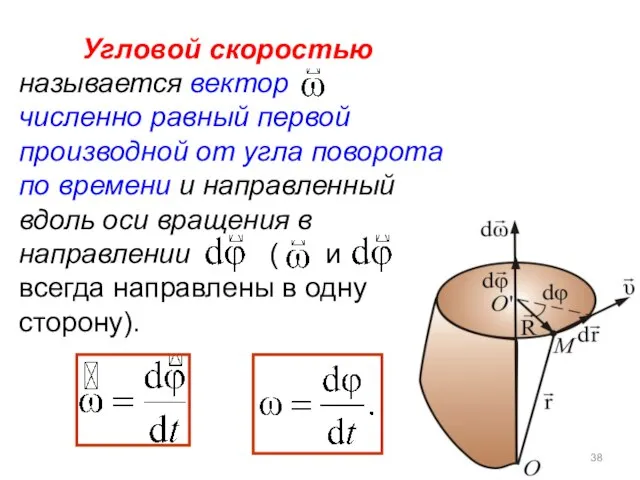
- 38. Угловой скоростью называется вектор численно равный первой производной от угла поворота по времени и направленный вдоль
- 39. Связь линейной и угловой скорости Пусть – линейная скорость точки М. За промежуток времени dt точка
- 40. Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на угол
- 41. Введем вектор углового ускорения для характеристики неравномерного вращения тела: Вектор направлен в ту же сторону, что
- 42. Выразим нормальное и тангенциальное ускорения точки М через угловую скорость и угловое ускорение:
- 43. Формулы простейших случаев вращения тела вокруг неподвижной оси: - равномерное вращение - равнопеременное вращение
- 44. Связь между линейными и угловыми величинами при вращательном движении:
- 48. Скачать презентацию


























 Спостереження фізичних явищ довкіля
Спостереження фізичних явищ довкіля Нестандартные уроки. Самостоятельно изучить на примере дисперсии света распространение световых волн в веществе
Нестандартные уроки. Самостоятельно изучить на примере дисперсии света распространение световых волн в веществе Электромагнитные волны и их свойства. Шкала электромагнитных волн
Электромагнитные волны и их свойства. Шкала электромагнитных волн Многократное отражение
Многократное отражение Механические колебания и волны
Механические колебания и волны Презентация по физике Динамика часть 4
Презентация по физике Динамика часть 4 Закон Кулона
Закон Кулона Вечер занимательной физики
Вечер занимательной физики Дисперсия света
Дисперсия света Электрический ток в биологических тканях. Основы реографии
Электрический ток в биологических тканях. Основы реографии Ядерный магнитный резонанс. Важнейшие области применения спектроскопии
Ядерный магнитный резонанс. Важнейшие области применения спектроскопии Учитель физики и информатики ДзагаловаТ.И. МОУ «Февральская СОШ№2» 2010г.
Учитель физики и информатики ДзагаловаТ.И. МОУ «Февральская СОШ№2» 2010г. Электричество и магнетизм. (Лекция 2-1)
Электричество и магнетизм. (Лекция 2-1) Одноканальная аппаратура тонального телеграфирования. Тракт передачи и приема аппаратуры. (Тема 8.2)
Одноканальная аппаратура тонального телеграфирования. Тракт передачи и приема аппаратуры. (Тема 8.2)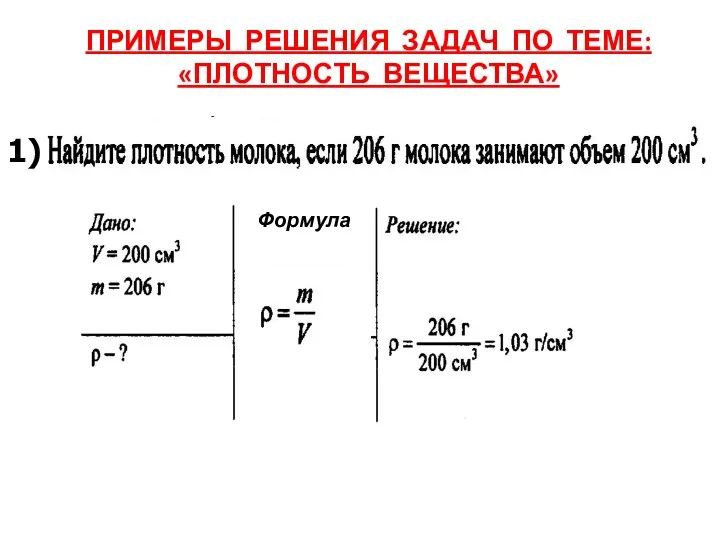 Плотность вещества
Плотность вещества Многоэлектронный атом (Лекция 8)
Многоэлектронный атом (Лекция 8) Ремонт гидравлического гасителя колебаний
Ремонт гидравлического гасителя колебаний Трансформатор
Трансформатор Движение в поле силы тяжести. Свободное падение
Движение в поле силы тяжести. Свободное падение Тепловые машины. (8 класс)
Тепловые машины. (8 класс) Презентация по физике "Интересная физика" - скачать
Презентация по физике "Интересная физика" - скачать  Використання магнітних полів в медицині
Використання магнітних полів в медицині Механические колебания. Свойства ультразвука
Механические колебания. Свойства ультразвука Мощность. Единицы измерения мощности
Мощность. Единицы измерения мощности Волновые методы геофизики (георадиолокация и сейсморазведка)
Волновые методы геофизики (георадиолокация и сейсморазведка) Силы упругости … если одна сила растягивает или изгибает ее на одно протяжение, то две изогнут ее на два [протяжения], три изогнут ее на три [протяжения] и так далее. Итак, поскольку теория очень коротка, постольку путь ее проверки очень прост.
Силы упругости … если одна сила растягивает или изгибает ее на одно протяжение, то две изогнут ее на два [протяжения], три изогнут ее на три [протяжения] и так далее. Итак, поскольку теория очень коротка, постольку путь ее проверки очень прост.  Электр тізбегінің резонансы. Резонанс кұбылысы және оның радиотехника және электрбайланыс магнасы
Электр тізбегінің резонансы. Резонанс кұбылысы және оның радиотехника және электрбайланыс магнасы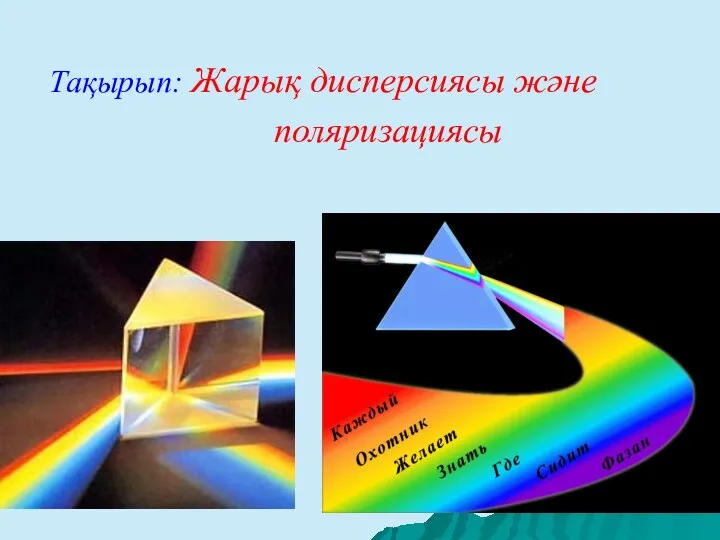 Жарық дисперсиясы және поляризациясы
Жарық дисперсиясы және поляризациясы