Содержание
- 2. Magnetism A Whole New Topic
- 3. DEMO
- 4. Magnetism Lodestone (Mineral) Lodestones attracted iron filings. Lodestones seemed to attract each other. Used as a
- 5. Magnetism Magnetism Refrigerators are attracted to magnets!
- 6. Magnetism Applications Motors Navigation – Compass Magnetic Tapes Music, Data Television Beam deflection Coil Magnetic Resonance
- 7. Magnetism Magnets Like Poles Repel Opposite Poles Attract Magnetic Poles are only found in pairs. No
- 8. Magnetism Observations Bring a magnet to a charged electroscope and nothing happens. No forces. Bring a
- 9. Magnetism Magnets Cutting a bar magnet in half produces TWO bar magnets, each with N and
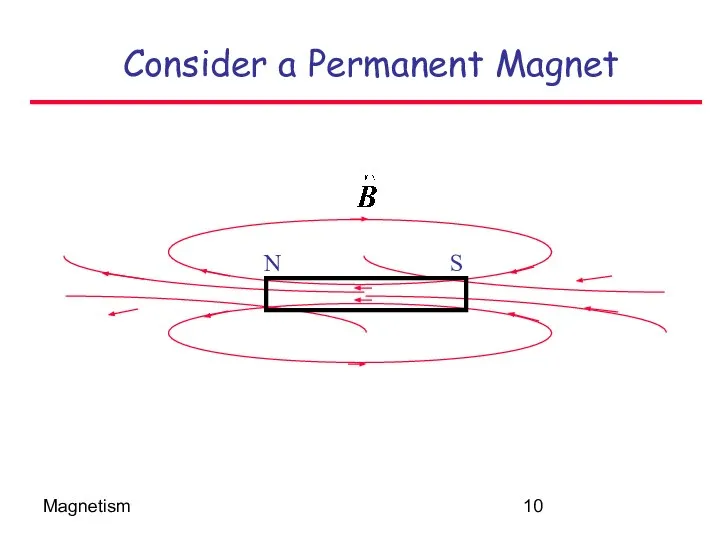
- 10. Magnetism Consider a Permanent Magnet
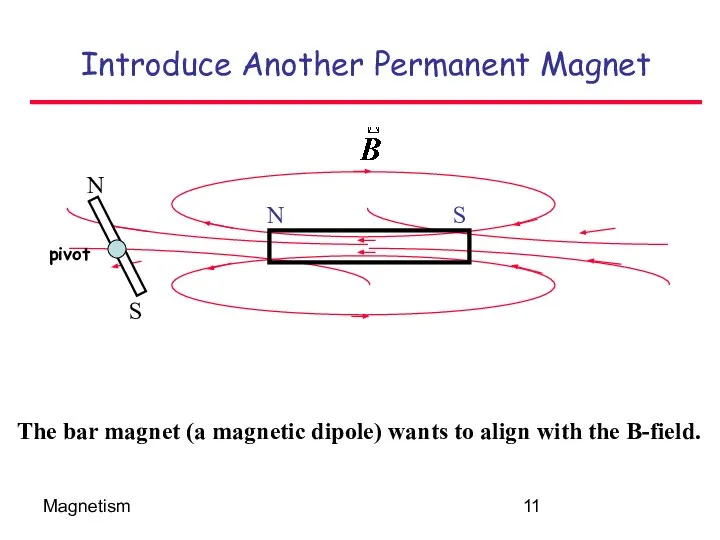
- 11. Magnetism Introduce Another Permanent Magnet The bar magnet (a magnetic dipole) wants to align with the
- 12. Magnetism The south pole of the small bar magnet is attracted towards the north pole of
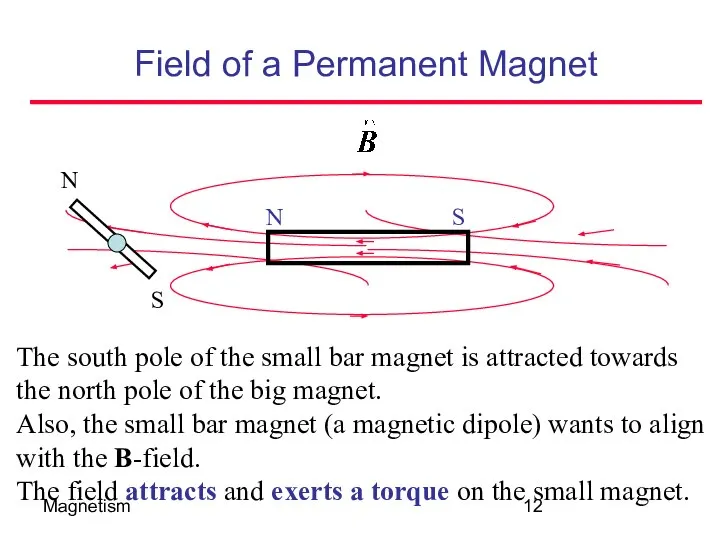
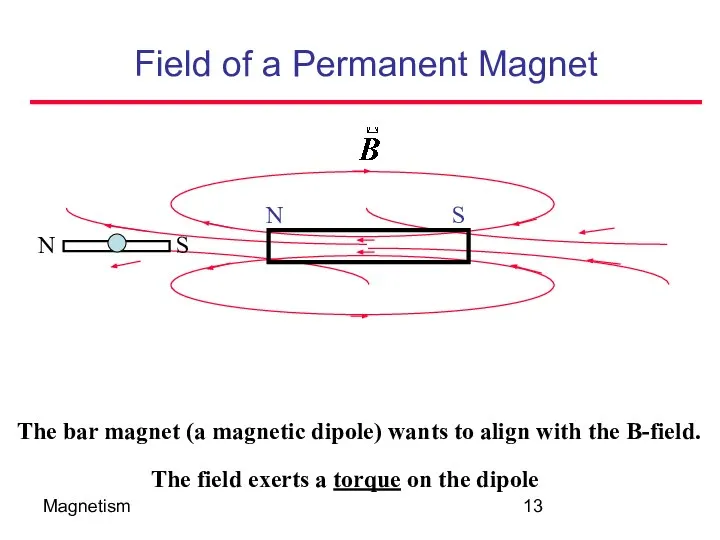
- 13. Magnetism Field of a Permanent Magnet The field exerts a torque on the dipole The bar
- 14. Magnetism The Magnetic Field Similar to Electric Field … exists in space. Has Magnitude AND Direction.
- 15. Magnetism Convention For Magnetic Fields X Field INTO Paper Field OUT of Paper B
- 16. Magnetism Experiments with Magnets Show Current carrying wire produces a circular magnetic field around it. Force
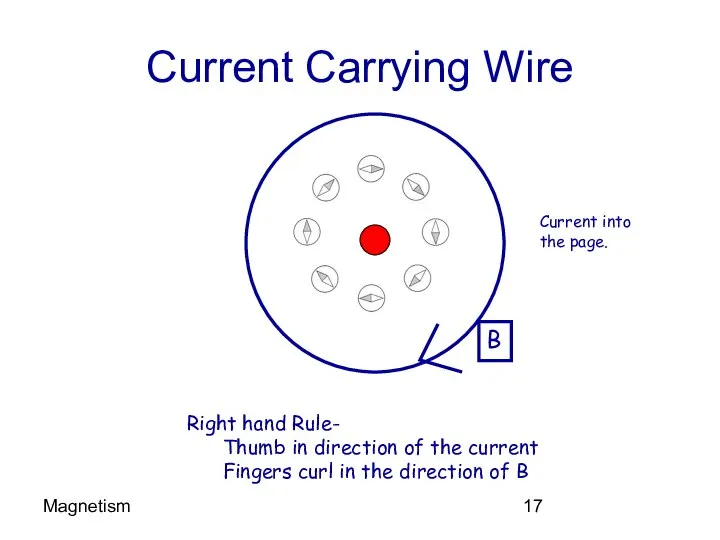
- 17. Magnetism Current Carrying Wire Current into the page. Right hand Rule- Thumb in direction of the
- 18. Magnetism Current Carrying Wire B field is created at ALL POINTS in space surrounding the wire.
- 19. Magnetism Compass and B Field Observations North Pole of magnets tend to move toward the direction
- 20. Magnetism Planet Earth
- 21. Magnetism Inside it all. 8000 Miles
- 22. Magnetism On the surface it looks like this..
- 23. Magnetism Inside: Warmer than Floriduh
- 24. Magnetism Much Warmer than Floriduh
- 25. Magnetism Finally
- 26. Magnetism In Between The molten iron core exists in a magnetic field that had been created
- 27. Magnetism After molten lava emerges from a volcano, it solidifies to a rock. In most cases
- 28. Magnetism Ancient Navigation
- 29. Magnetism This planet is really screwed up! NORTH POLE SOUTH POLE
- 30. Magnetism Repeat Navigation DIRECTION N S If N direction is pointed to by the NORTH pole
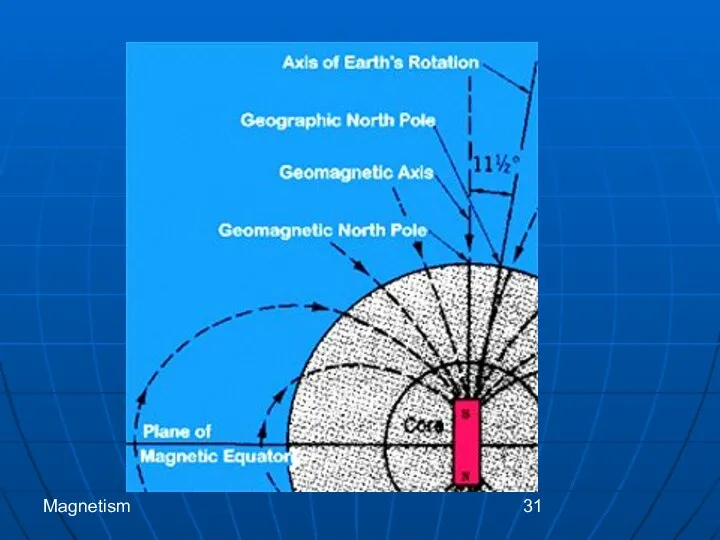
- 31. Magnetism
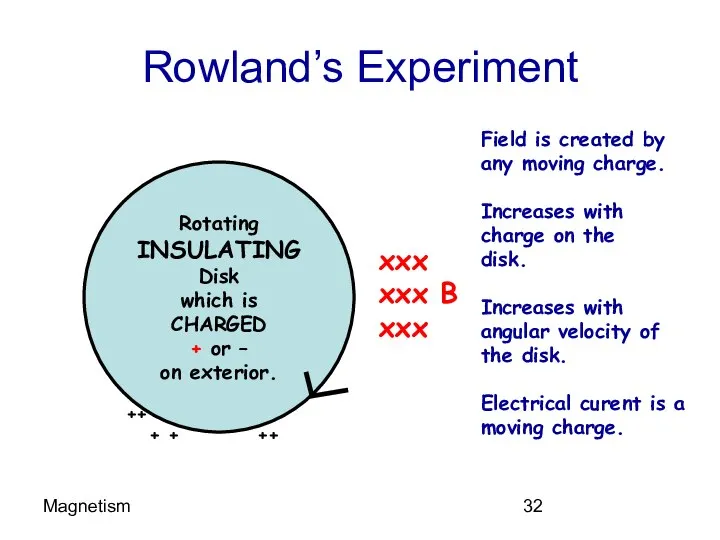
- 32. Magnetism Rowland’s Experiment Rotating INSULATING Disk which is CHARGED + or – on exterior. xxx xxx
- 33. Magnetism A Look at the Physics There is NO force on a charge placed into a
- 34. Magnetism WHAT THE HECK IS THAT??? A WHAT PRODUCT? A CROSS PRODUCT – Like an angry
- 35. Magnetism The Lorentz Force This can be summarized as: v F B q m or: θ
- 36. Magnetism Note B is sort of the Force per unit (charge-velocity) Whatever that is!!
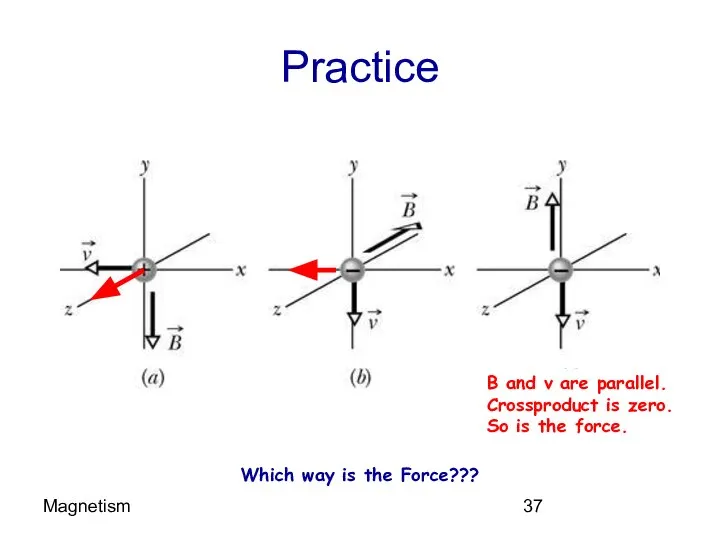
- 37. Magnetism Practice Which way is the Force??? B and v are parallel. Crossproduct is zero. So
- 38. Magnetism Units
- 39. Magnetism teslas are HUGE!
- 40. Magnetism The Magnetic Force is Different From the Electric Force. Whereas the electric force acts in
- 41. Magnetism So… A moving charge can create a magnetic field. A moving charge is acted upon
- 42. Magnetism Trajectory of Charged Particles in a Magnetic Field + + + + + + +
- 43. Magnetism Trajectory of Charged Particles in a Magnetic Field + + + + + + +
- 44. Magnetism Review of Rotational Motion
- 45. Magnetism YES ! You have to remember this stuff.
- 46. Magnetism + + + + + + + + + + + + + + +
- 47. Magnetism Cyclotron Frequency The time taken to complete one orbit is: V cancels !
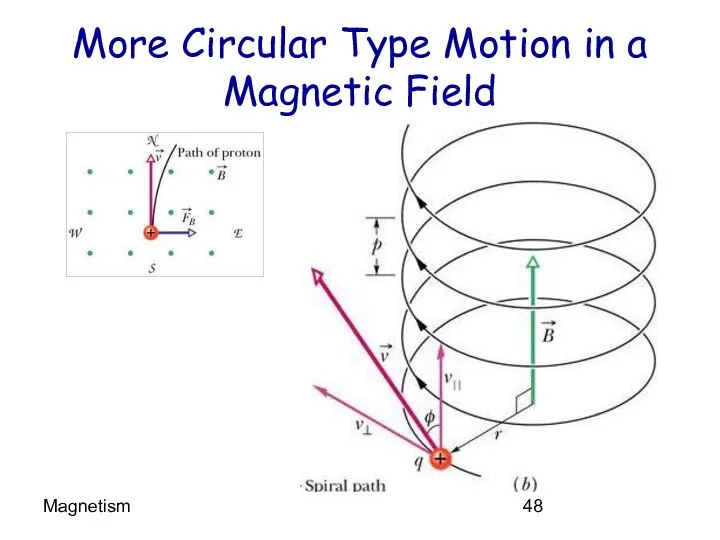
- 48. Magnetism More Circular Type Motion in a Magnetic Field
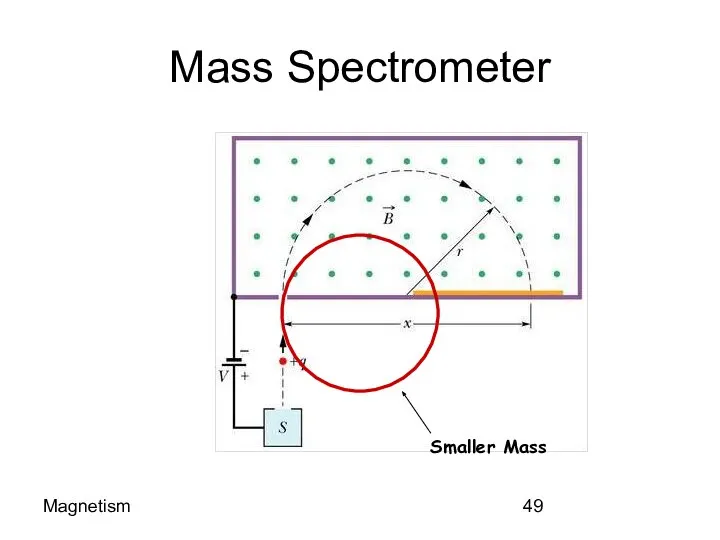
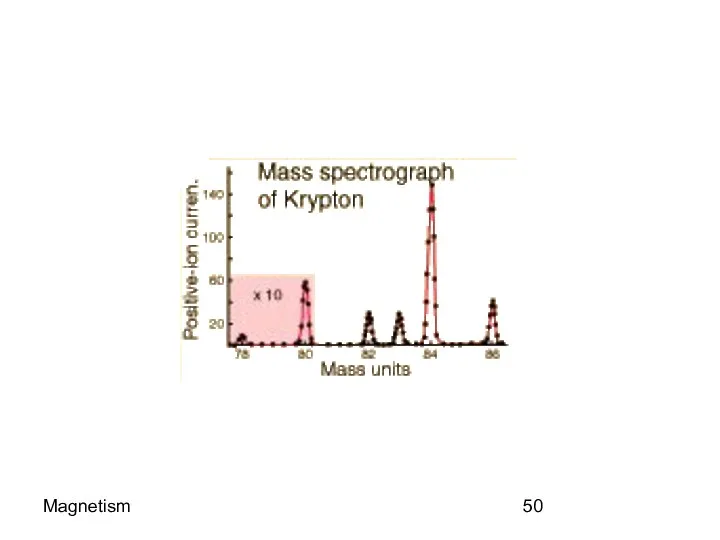
- 49. Magnetism Mass Spectrometer
- 50. Magnetism
- 51. Magnetism Cyclotron Frequency The time taken to complete one orbit is: V cancels !
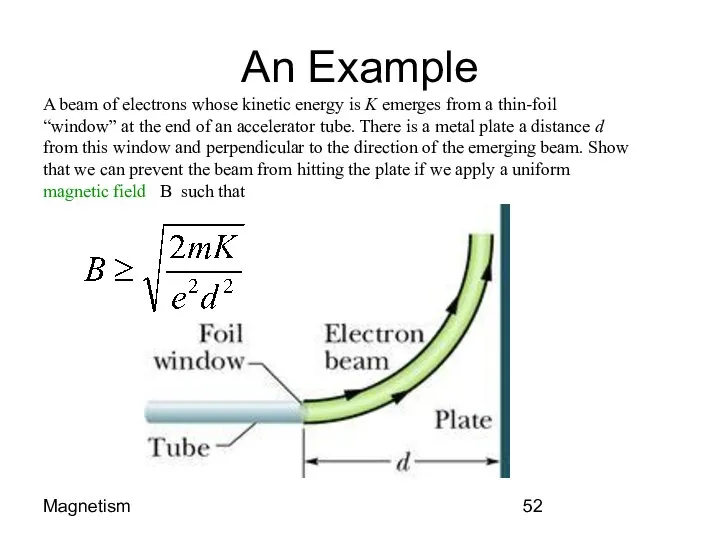
- 52. Magnetism An Example A beam of electrons whose kinetic energy is K emerges from a thin-foil
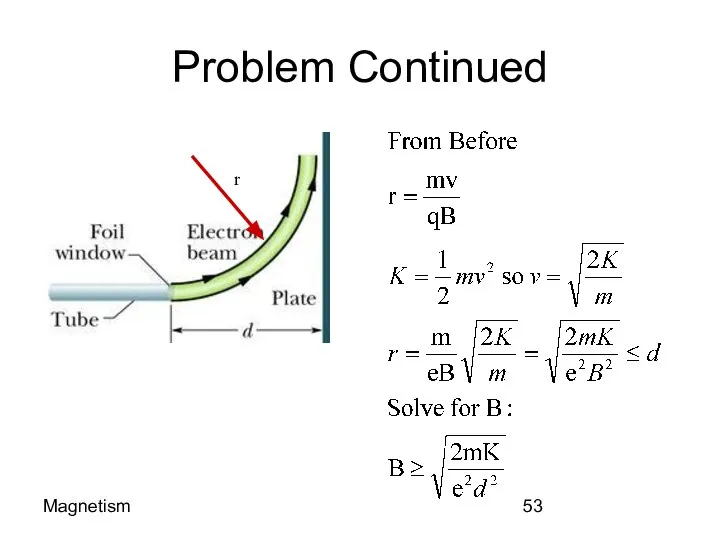
- 53. Magnetism Problem Continued
- 54. Some New Stuff Magnetism and Forces
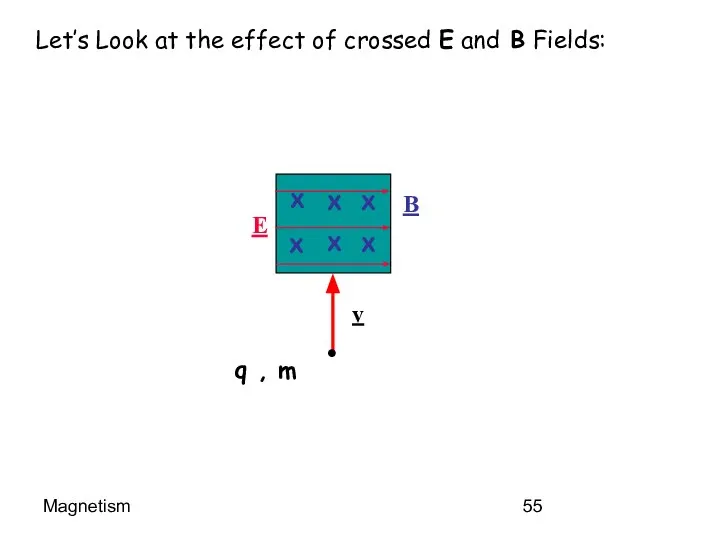
- 55. Magnetism Let’s Look at the effect of crossed E and B Fields: x x x x
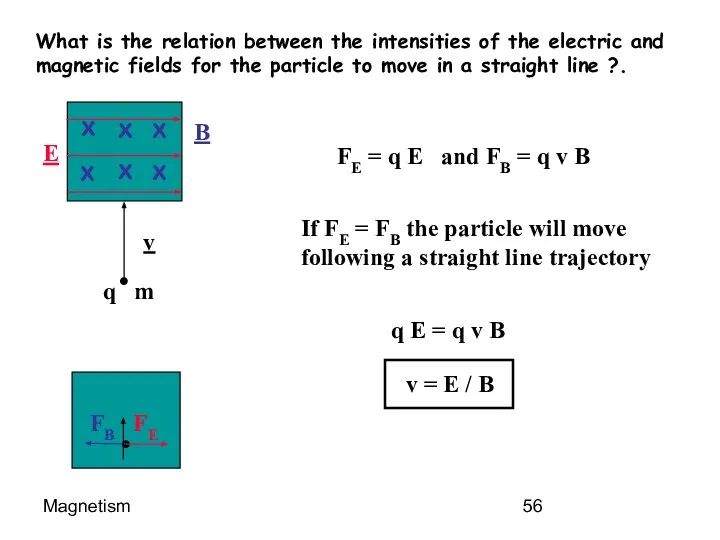
- 56. Magnetism What is the relation between the intensities of the electric and magnetic fields for the
- 57. Magnetism What does this mean?? This equation only contains the E and B fields in it.
- 58. Magnetism “Real” Mass Spectrometer Create ions from injected species. This will contain various masses, charges and
- 59. Magnetism Components of MS:
- 60. Magnetism Remember: THESE "E and B" GUYS ARE VECTORS! Let's Look at an example...
- 61. Magnetism VECTOR CALCULATIONS
- 62. Magnetism Problem: A Vector Example A proton of charge +e and mass m is projected into
- 63. Magnetism More
- 64. Magnetism New Topic Forces on Wires
- 65. Magnetism Wires A wire with a current contains moving charges. A magnetic field will apply a
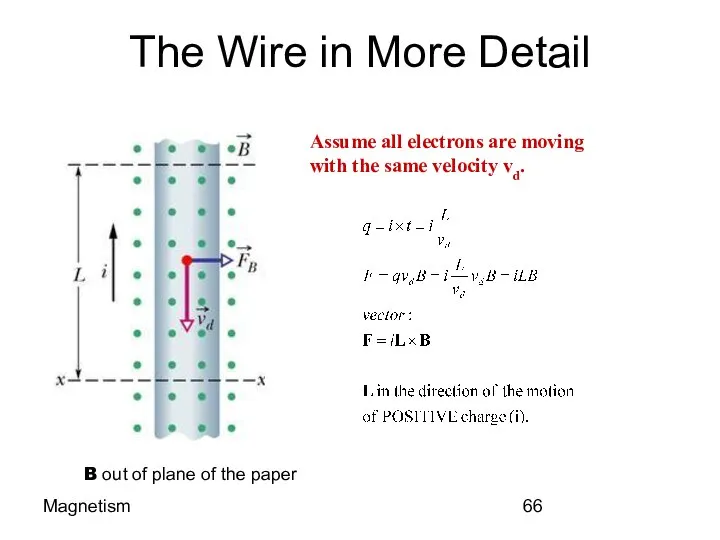
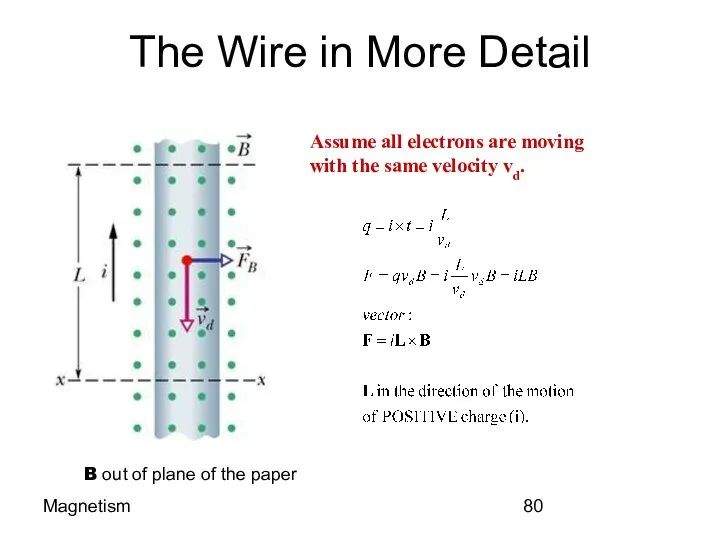
- 66. Magnetism The Wire in More Detail B out of plane of the paper Assume all electrons
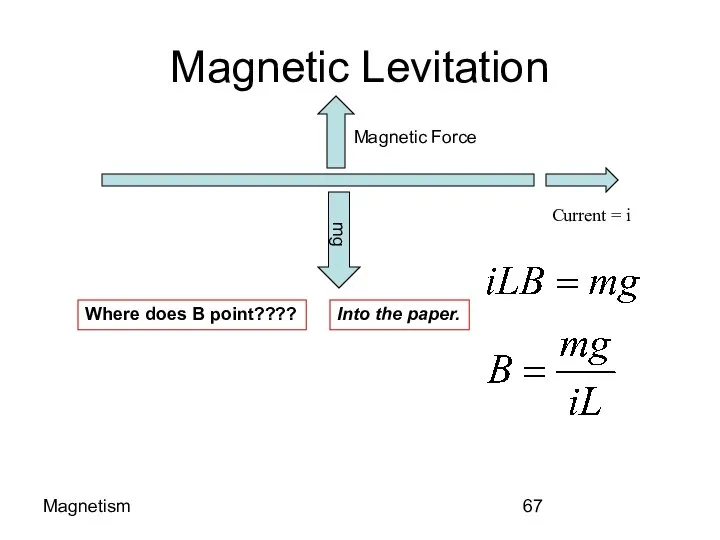
- 67. Magnetism Magnetic Levitation mg Where does B point???? Into the paper.
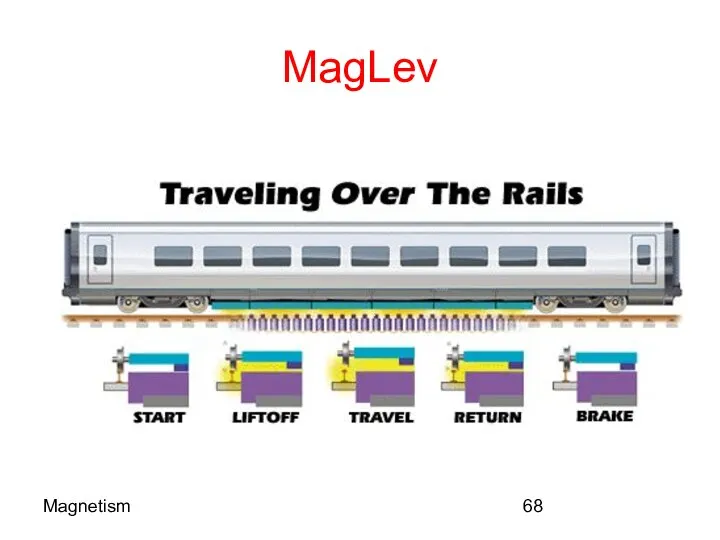
- 68. Magnetism MagLev
- 69. Magnetism Magnetic Repulsion
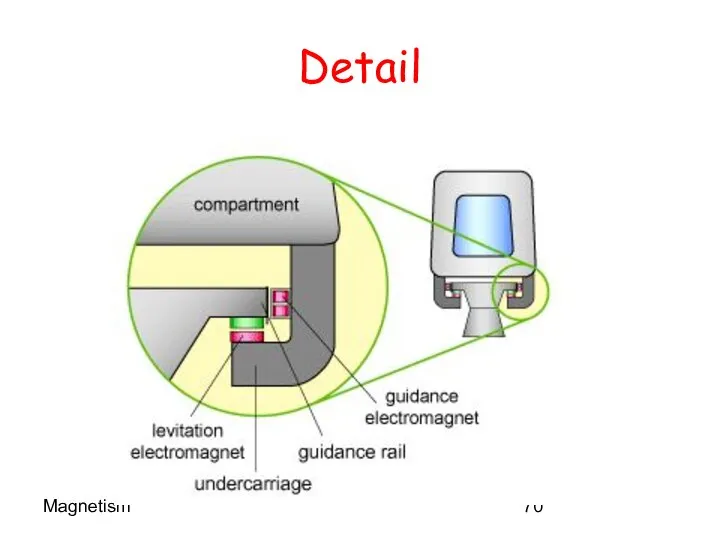
- 70. Magnetism Detail
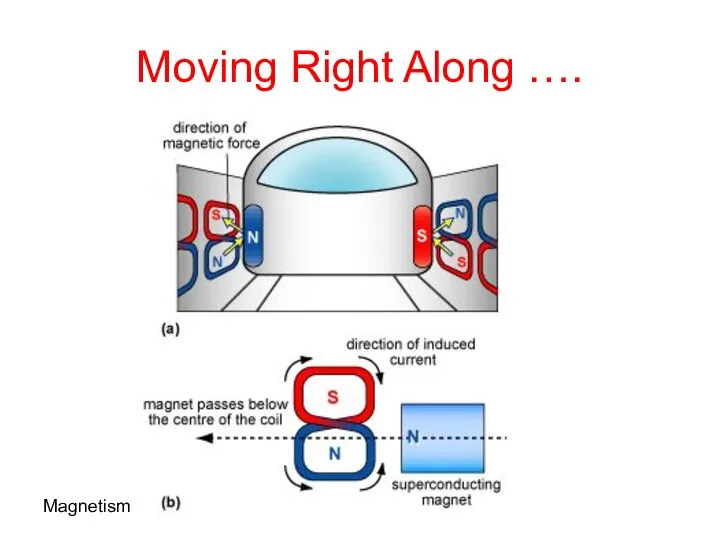
- 71. Magnetism Moving Right Along ….
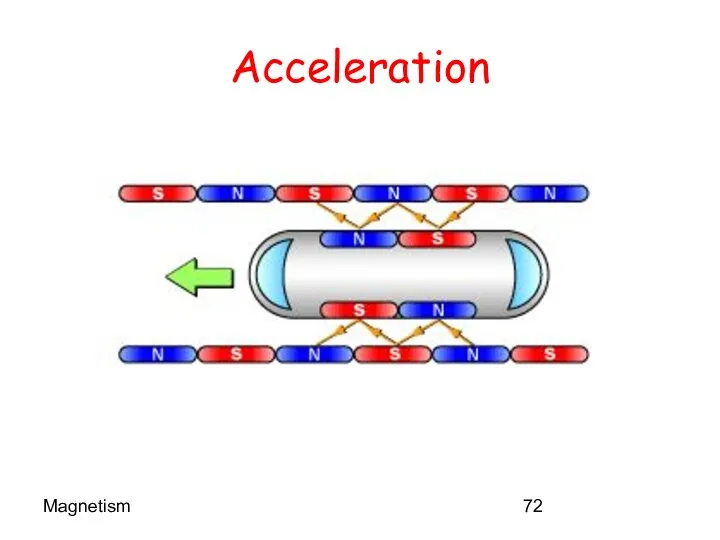
- 72. Magnetism Acceleration
- 73. Magnetism Don’t Buy A Ticket Quite Yet.. This is still experimental. Much development still required. Some
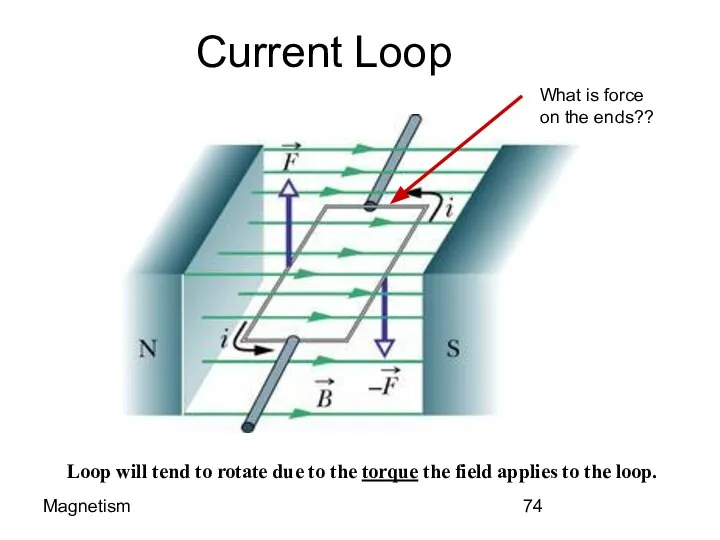
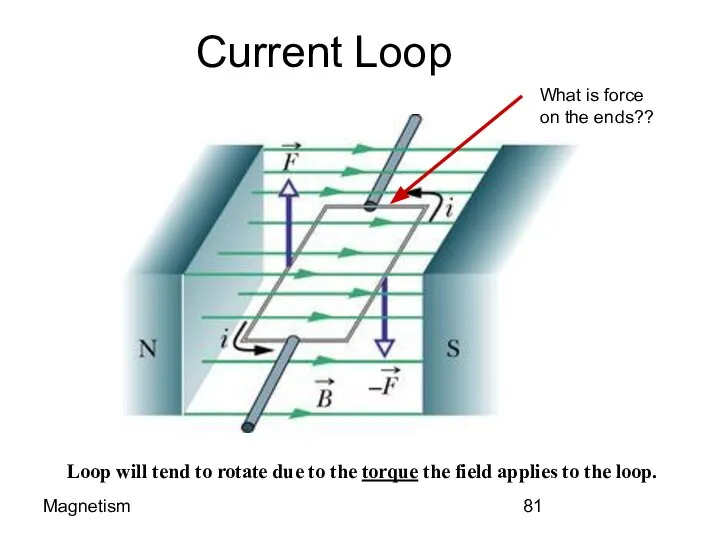
- 74. Magnetism Current Loop Loop will tend to rotate due to the torque the field applies to
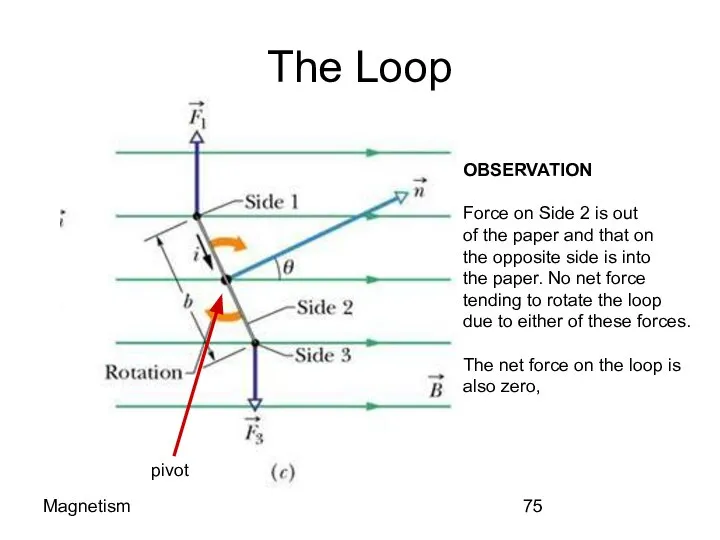
- 75. Magnetism The Loop OBSERVATION Force on Side 2 is out of the paper and that on
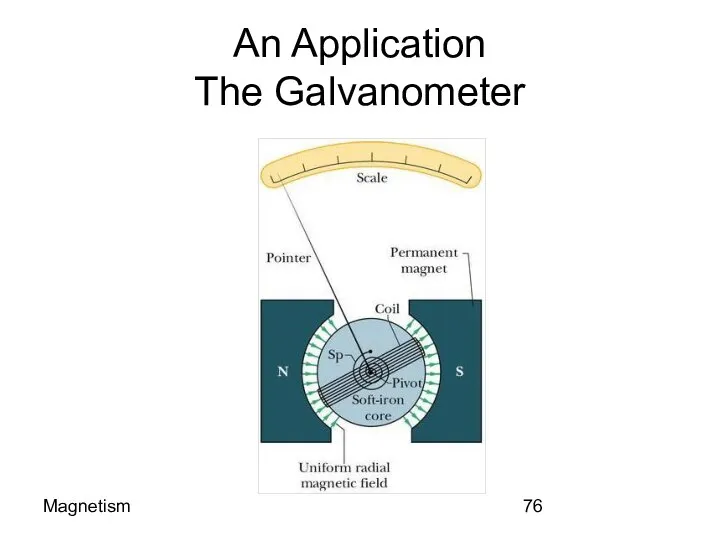
- 76. Magnetism An Application The Galvanometer
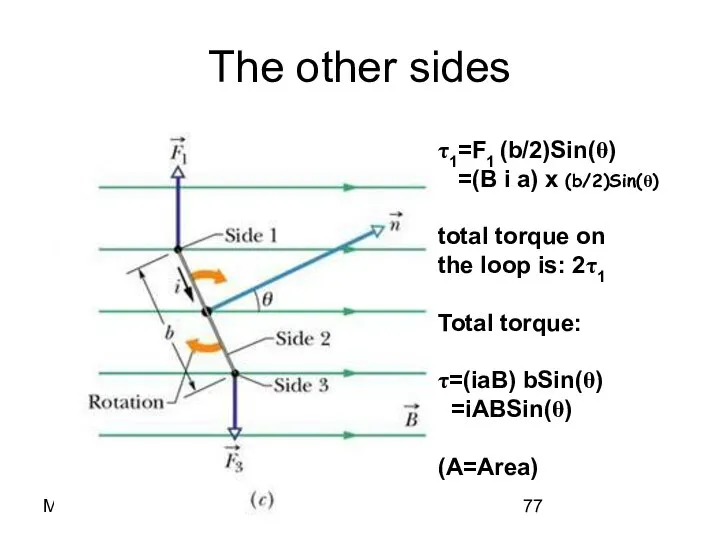
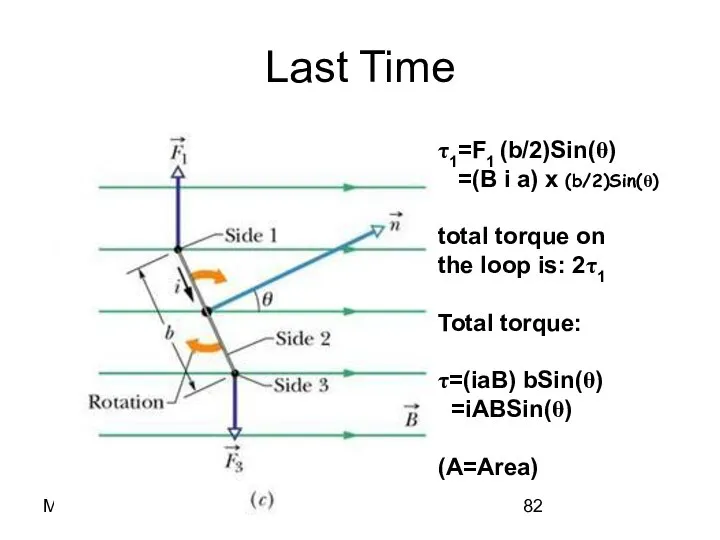
- 77. Magnetism The other sides τ1=F1 (b/2)Sin(θ) =(B i a) x (b/2)Sin(θ) total torque on the loop
- 78. Magnetism Watcha Gonna Do Quiz Today Return to Magnetic Material Exams not yet returned. Sorry.
- 79. Magnetism Wires A wire with a current contains moving charges. A magnetic field will apply a
- 80. Magnetism The Wire in More Detail B out of plane of the paper Assume all electrons
- 81. Magnetism Current Loop Loop will tend to rotate due to the torque the field applies to
- 82. Magnetism Last Time τ1=F1 (b/2)Sin(θ) =(B i a) x (b/2)Sin(θ) total torque on the loop is:
- 83. Magnetism A Coil Normal to the coil RIGHT HAND RULE TO FIND NORMAL TO THE COIL:
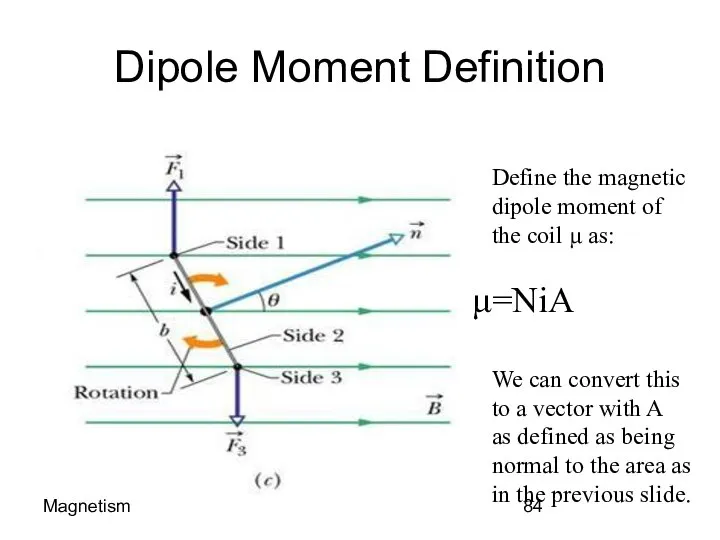
- 84. Magnetism Dipole Moment Definition Define the magnetic dipole moment of the coil μ as: =NiA We
- 85. Magnetism Current Loop
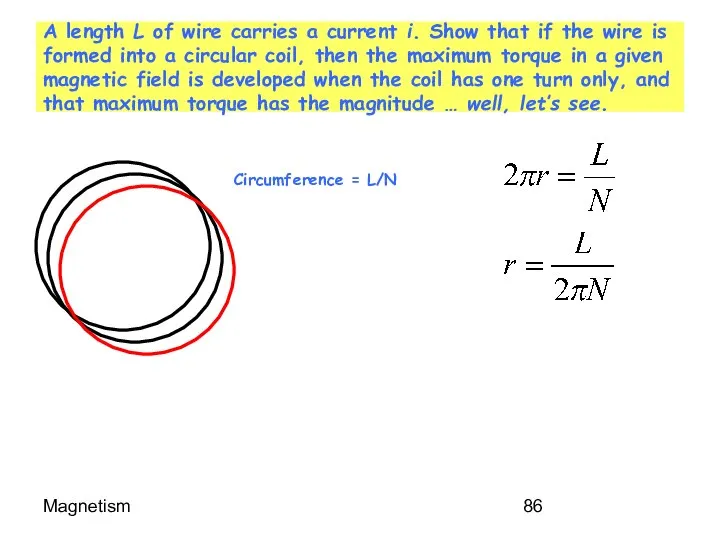
- 86. Magnetism A length L of wire carries a current i. Show that if the wire is
- 87. Magnetism Problem continued…
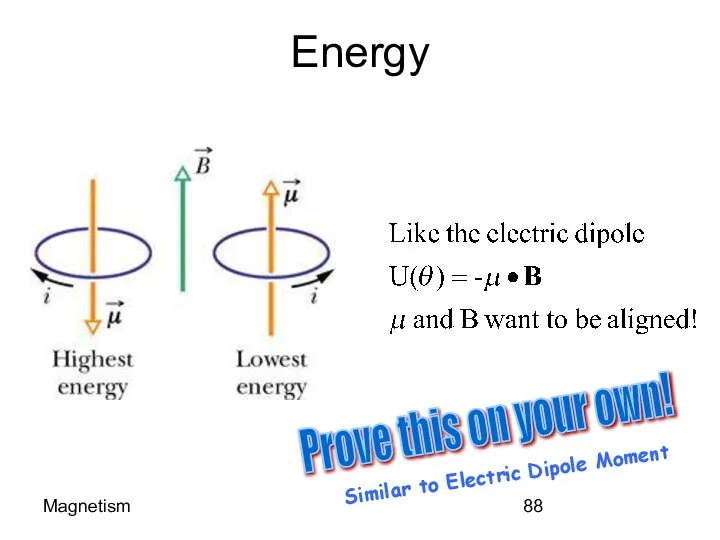
- 88. Magnetism Energy
- 89. The Hall Effect
- 90. Magnetism What Does it Do? Allows the measurement of Magnetic Field if a material is known.
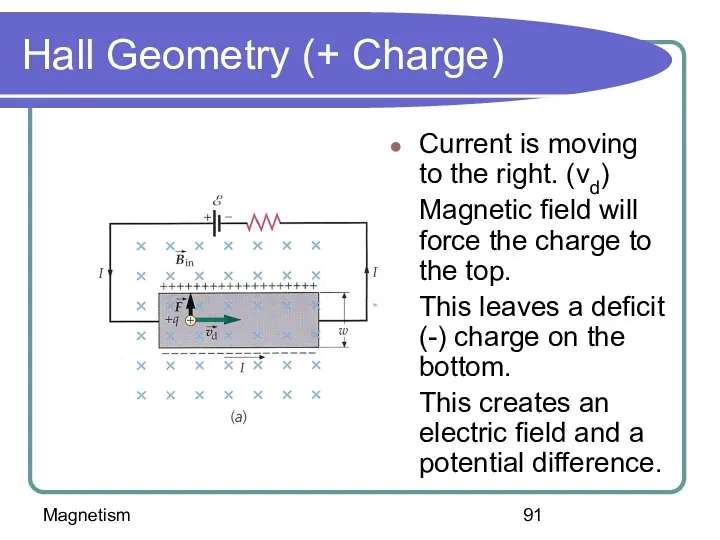
- 91. Magnetism Hall Geometry (+ Charge) Current is moving to the right. (vd) Magnetic field will force
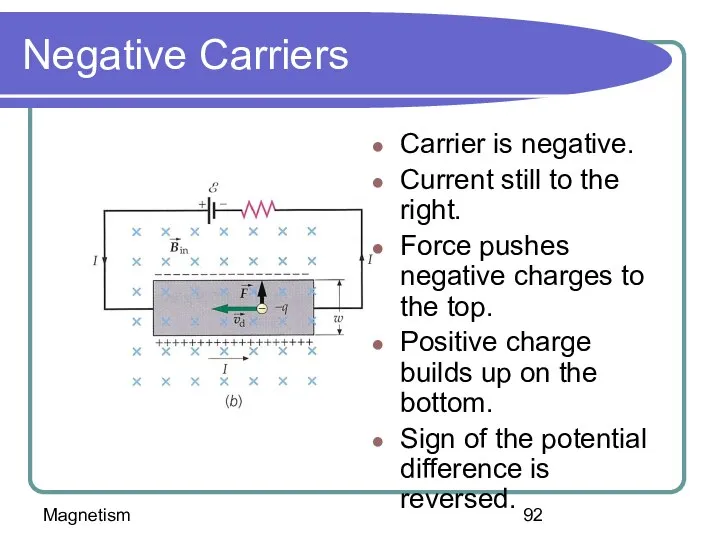
- 92. Magnetism Negative Carriers Carrier is negative. Current still to the right. Force pushes negative charges to
- 93. Magnetism Hall Math Eventually, the field due to the Hall effect will allow the current to
- 94. Magnetic Fields Due to Currents Chapter 30
- 95. Magnetism Try to remember…
- 96. Magnetism For the Magnetic Field, current “elements” create the field. This, defines B! This is the
- 97. Magnetism Magnetic Field of a Straight Wire We intimated via magnets that the Magnetic field associated
- 98. Magnetism From the Past
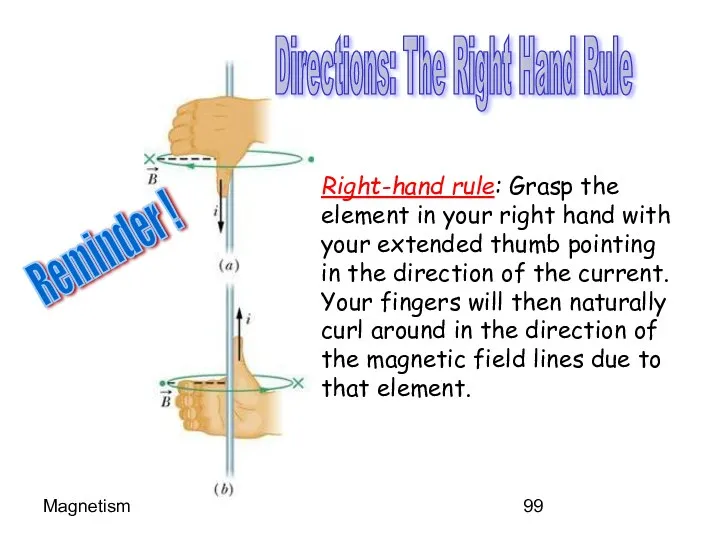
- 99. Magnetism Right-hand rule: Grasp the element in your right hand with your extended thumb pointing in
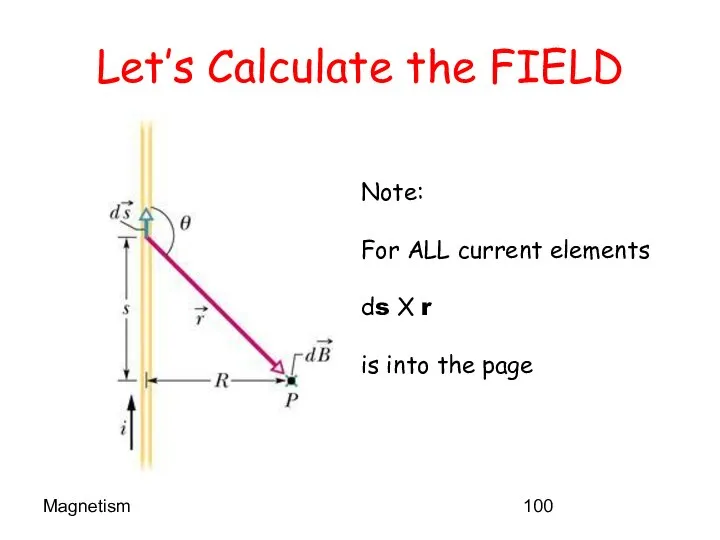
- 100. Magnetism Let’s Calculate the FIELD Note: For ALL current elements ds X r is into the
- 101. Magnetism The Details
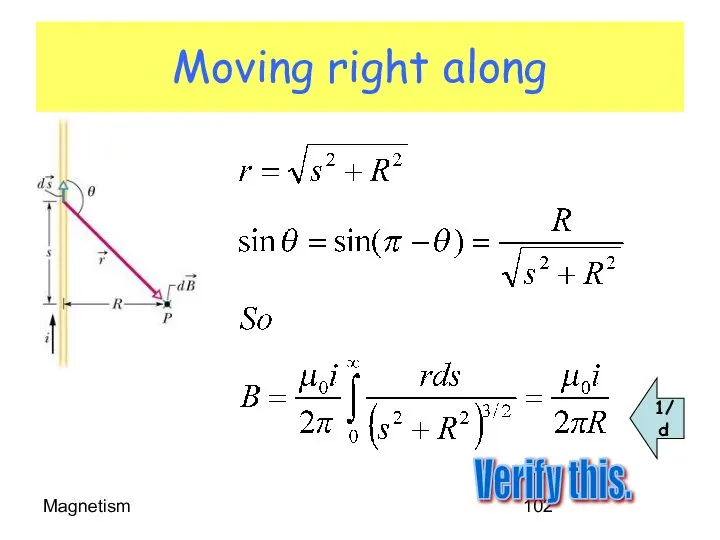
- 102. Magnetism Moving right along Verify this. 1/d
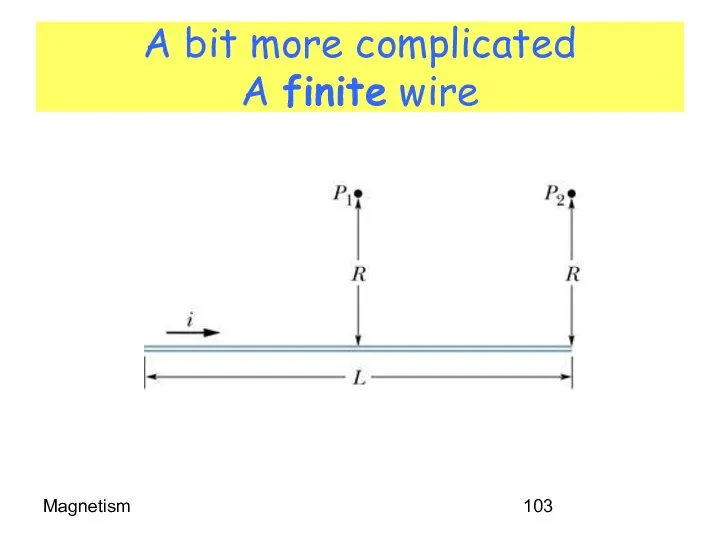
- 103. Magnetism A bit more complicated A finite wire
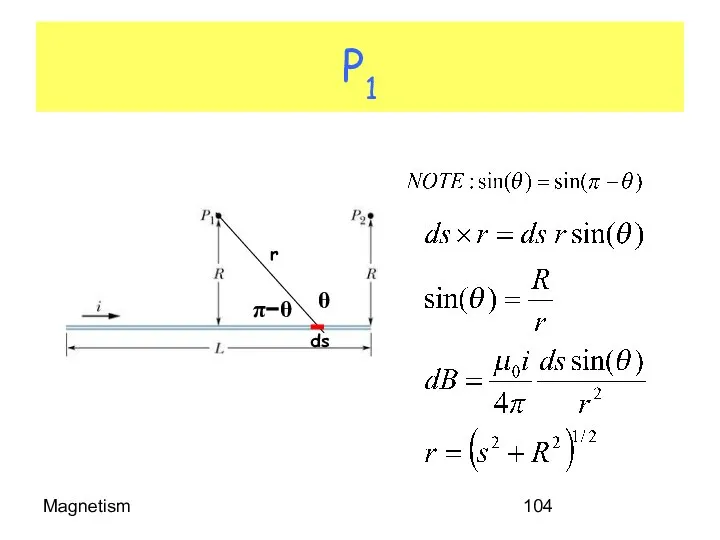
- 104. Magnetism P1
- 105. Magnetism More P1
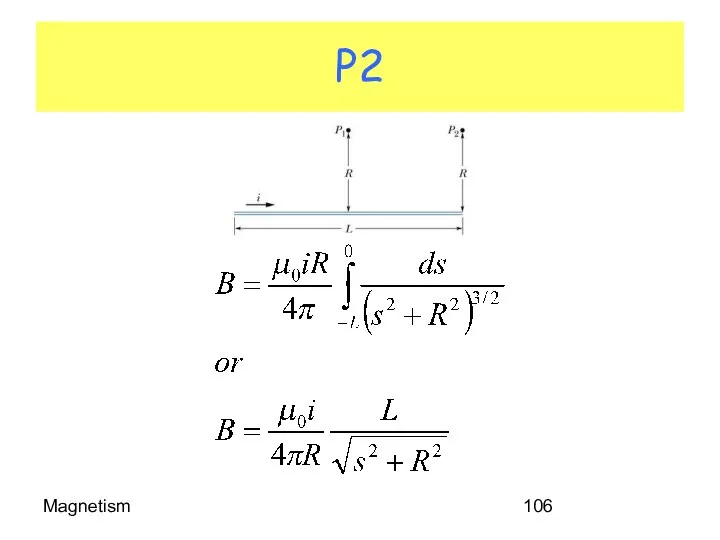
- 106. Magnetism P2
- 107. Magnetism APPLICATION: Find the magnetic field B at point P in for i = 10 A
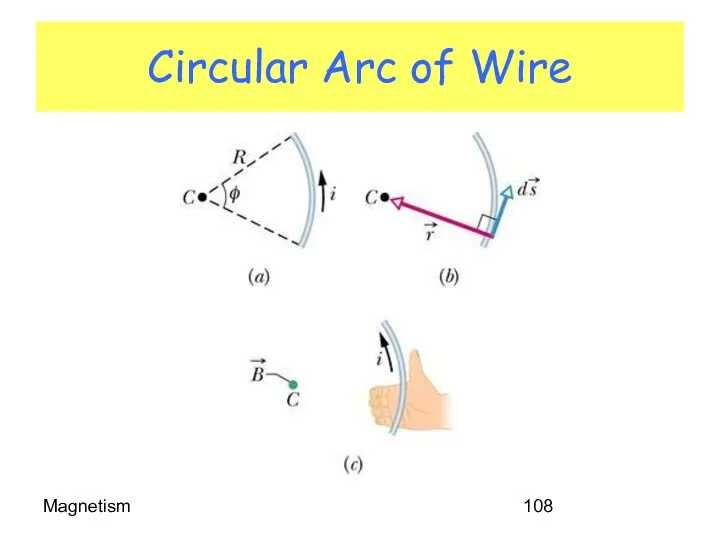
- 108. Magnetism Circular Arc of Wire
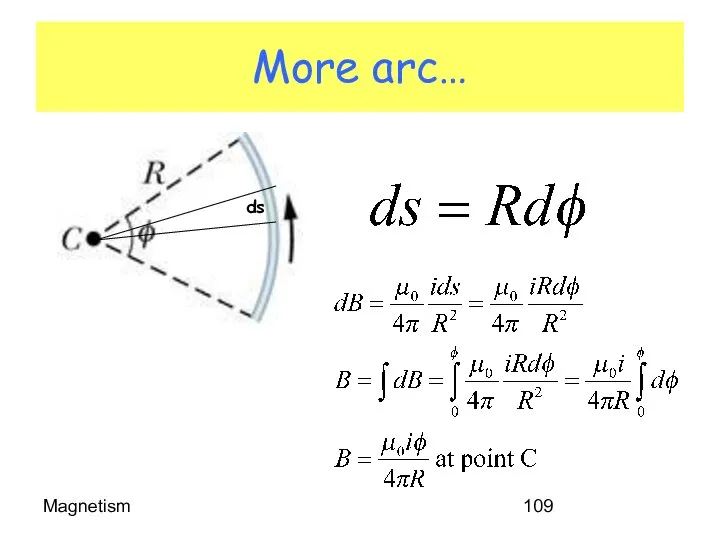
- 109. Magnetism More arc…
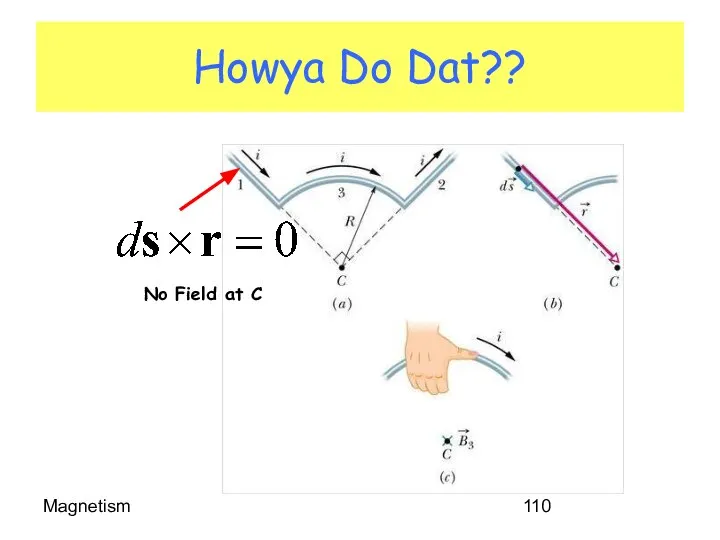
- 110. Magnetism Howya Do Dat?? No Field at C
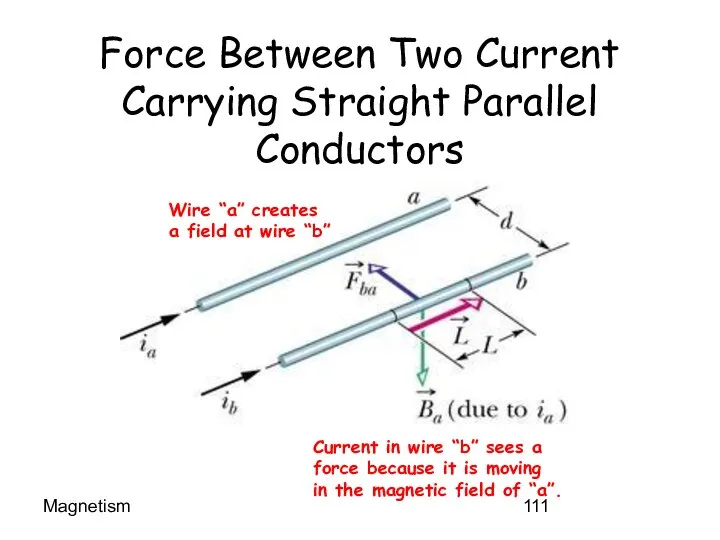
- 111. Magnetism Force Between Two Current Carrying Straight Parallel Conductors Wire “a” creates a field at wire
- 112. Magnetism The Calculation
- 113. Magnetism Definition of the Ampere The force acting between currents in parallel wires is the basis
- 114. TRANSITION AMPERE
- 115. Welcome to Andre’ Marie Ampere’s Law Normally written as a “circulation” vector equation. We will look
- 116. Magnetism Remember GAUSS’S LAW?? Surface Integral
- 117. Magnetism Gauss’s Law Made calculations easier than integration over a charge distribution. Applied to situations of
- 118. Magnetism The next few slides have been lifted from Seb Oliver on the internet Whoever he
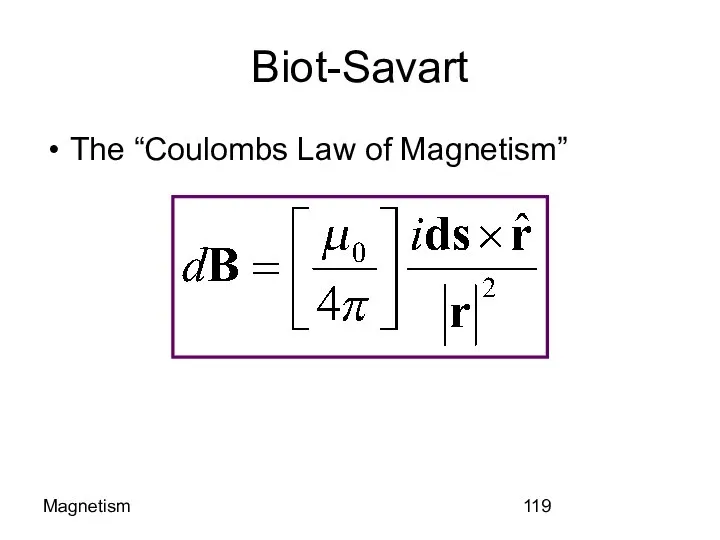
- 119. Magnetism Biot-Savart The “Coulombs Law of Magnetism”
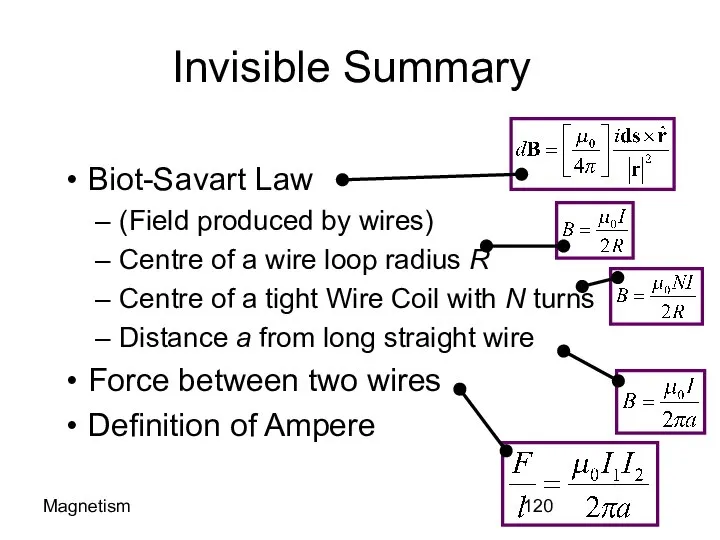
- 120. Magnetism Invisible Summary Biot-Savart Law (Field produced by wires) Centre of a wire loop radius R
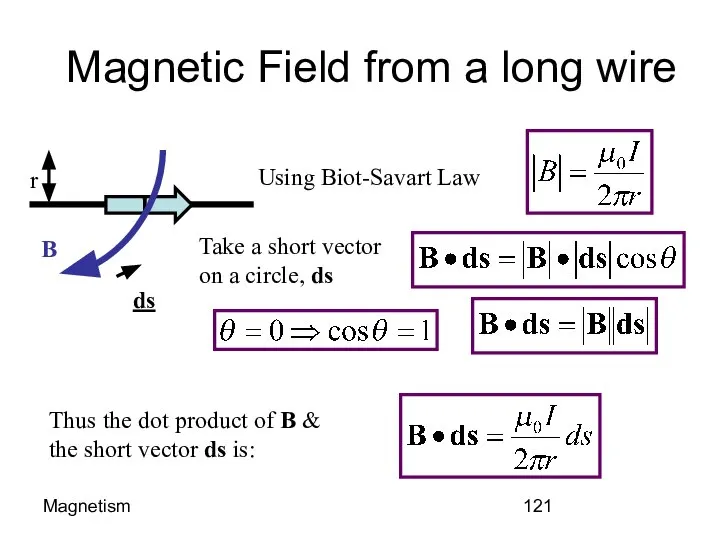
- 121. Magnetism Magnetic Field from a long wire I B r ds Using Biot-Savart Law Take a
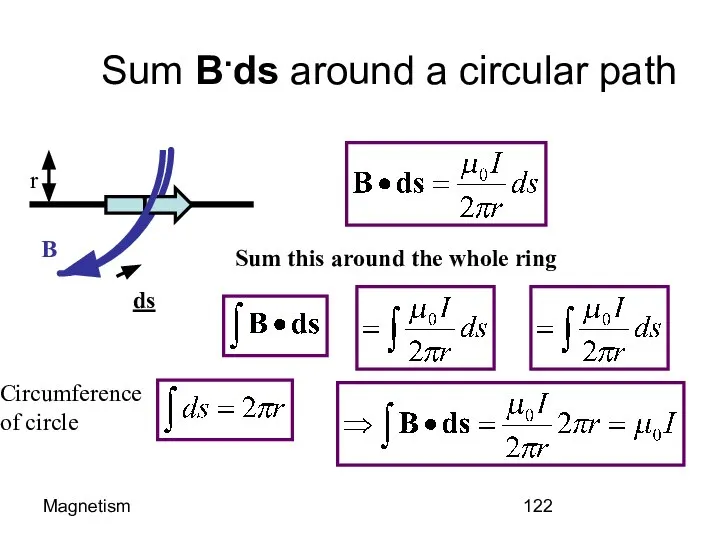
- 122. Magnetism Sum B.ds around a circular path I B r ds Sum this around the whole
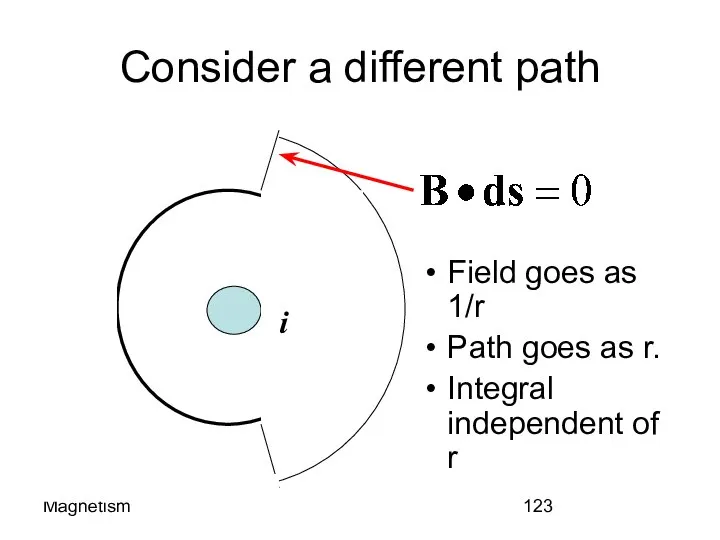
- 123. Magnetism Consider a different path Field goes as 1/r Path goes as r. Integral independent of
- 124. Magnetism SO, AMPERE’S LAW by SUPERPOSITION: We will do a LINE INTEGRATION Around a closed path
- 125. Magnetism Ampere’s Law USE THE RIGHT HAND RULE IN THESE CALCULATIONS
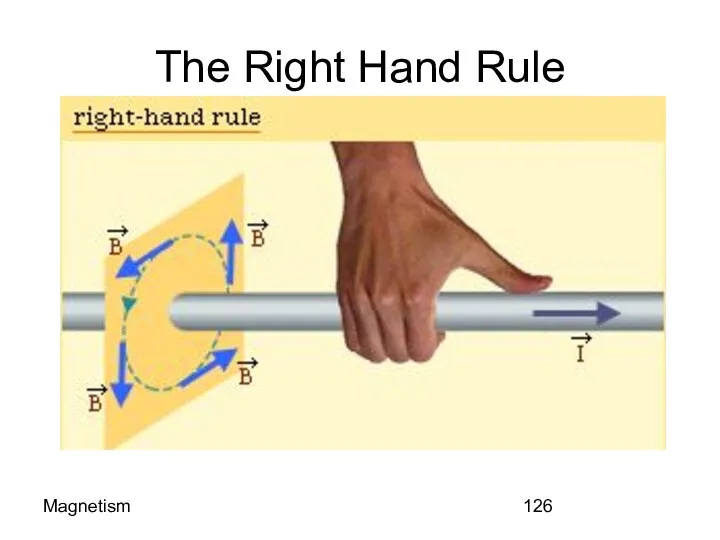
- 126. Magnetism The Right Hand Rule
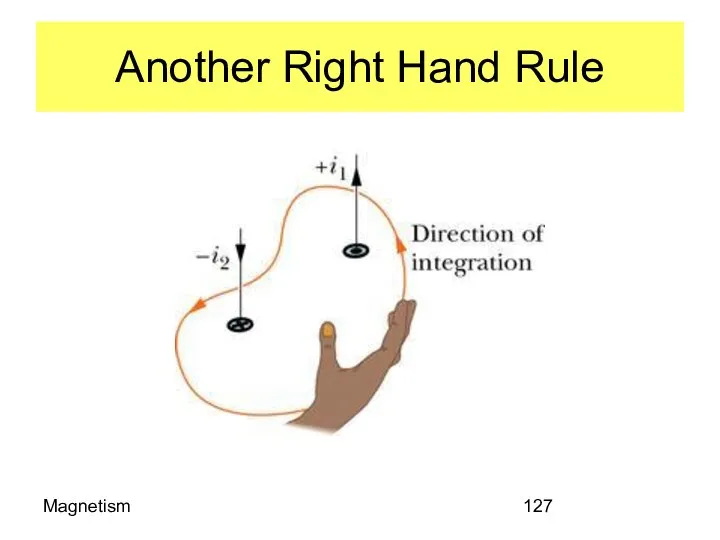
- 127. Magnetism Another Right Hand Rule
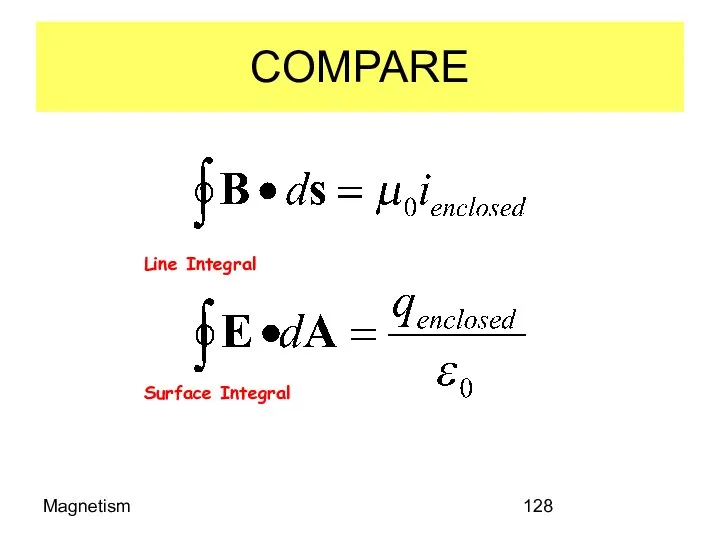
- 128. Magnetism COMPARE Line Integral Surface Integral
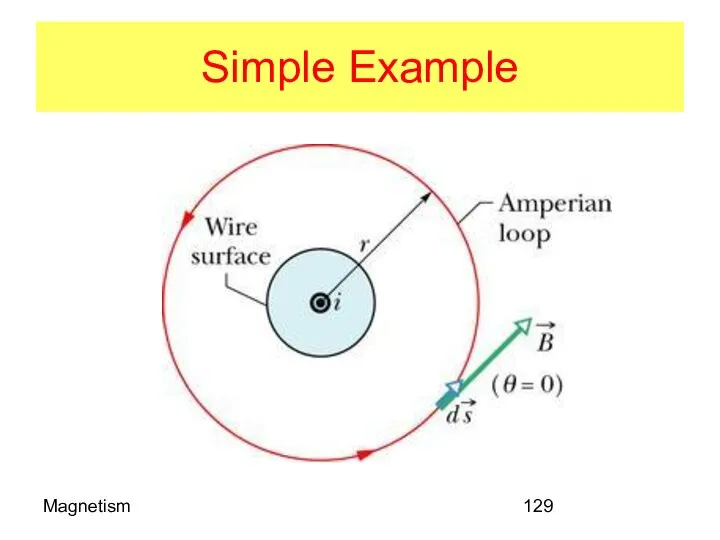
- 129. Magnetism Simple Example
- 130. Magnetism Field Around a Long Straight Wire
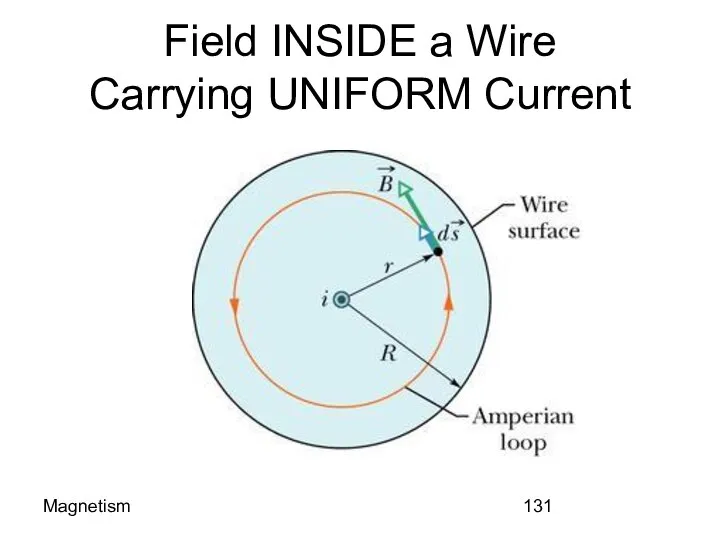
- 131. Magnetism Field INSIDE a Wire Carrying UNIFORM Current
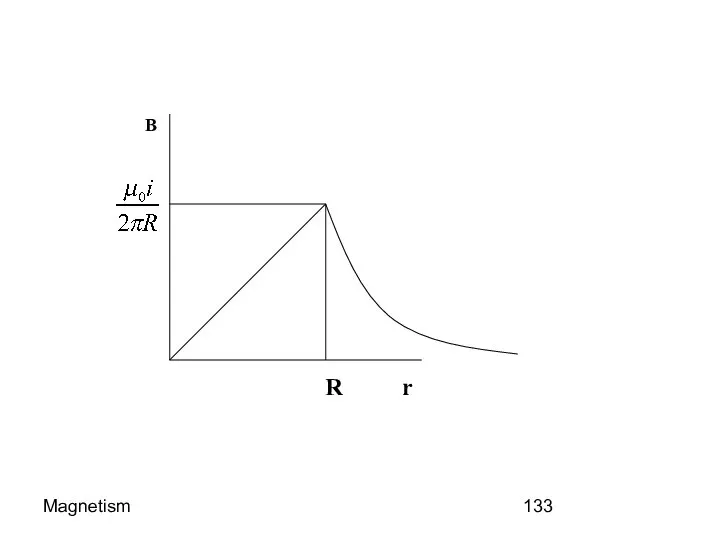
- 132. Magnetism The Calculation Graph ????
- 133. Magnetism
- 134. Magnetism Procedure Apply Ampere’s law only to highly symmetrical situations. Superposition works. Two wires can be
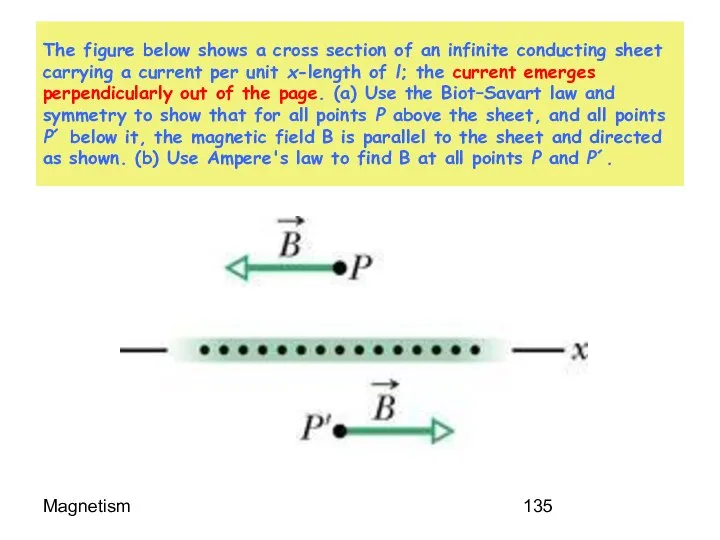
- 135. Magnetism The figure below shows a cross section of an infinite conducting sheet carrying a current
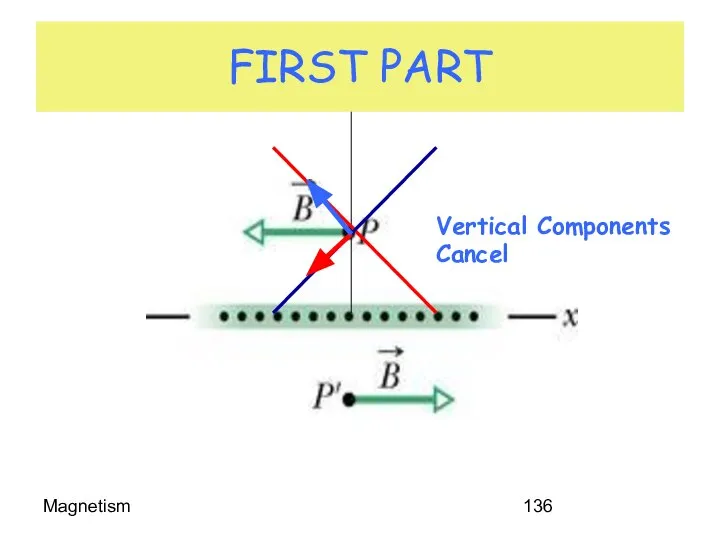
- 136. Magnetism FIRST PART Vertical Components Cancel
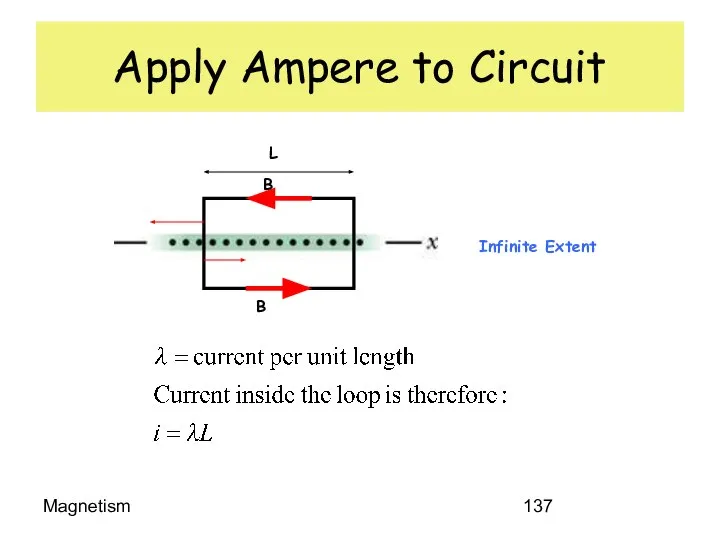
- 137. Magnetism Apply Ampere to Circuit
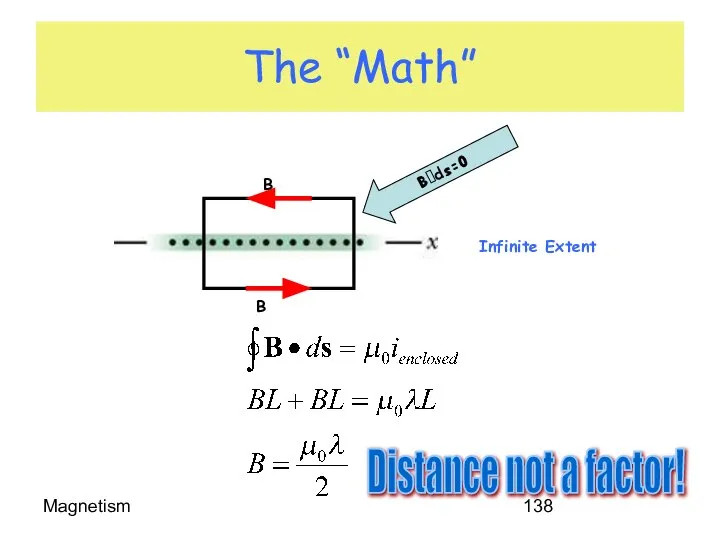
- 138. Magnetism The “Math” Bds=0 Distance not a factor!
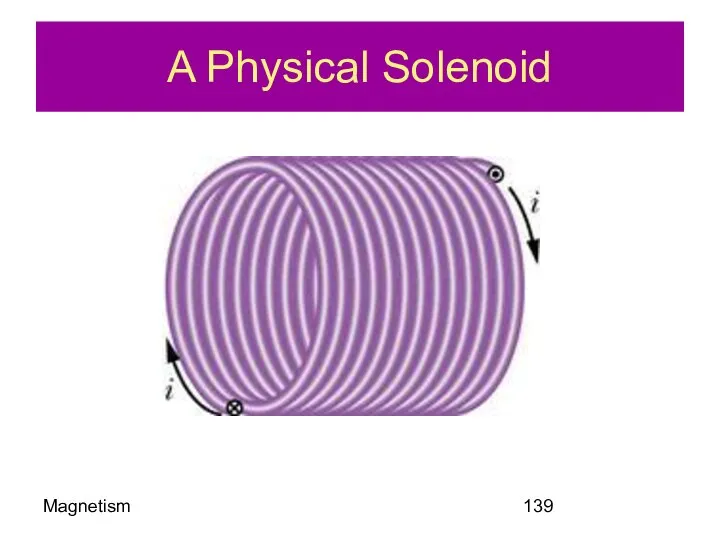
- 139. Magnetism A Physical Solenoid
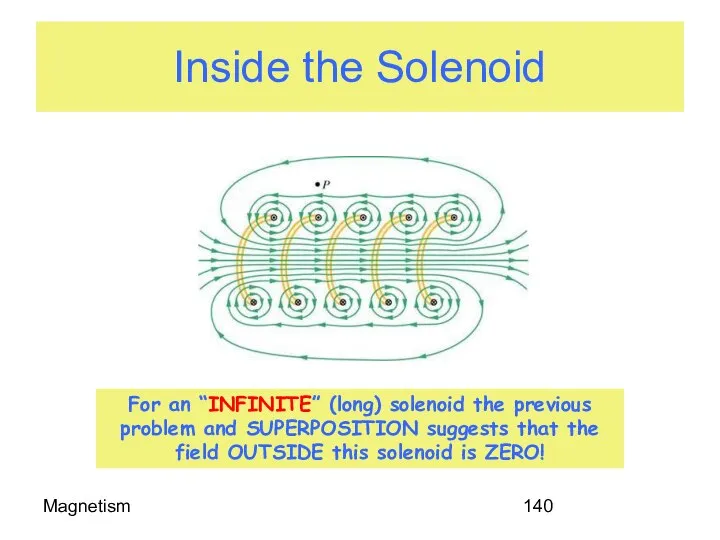
- 140. Magnetism Inside the Solenoid For an “INFINITE” (long) solenoid the previous problem and SUPERPOSITION suggests that
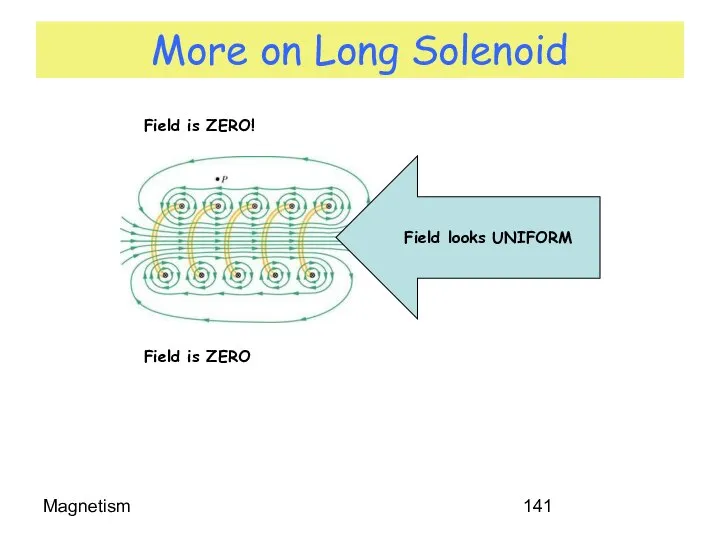
- 141. Magnetism More on Long Solenoid Field is ZERO! Field is ZERO Field looks UNIFORM
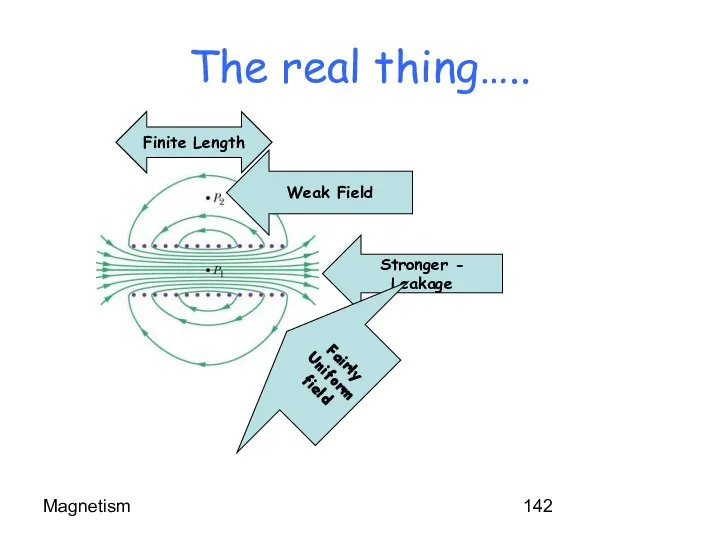
- 142. Magnetism The real thing….. Weak Field Stronger - Leakage Fairly Uniform field Finite Length
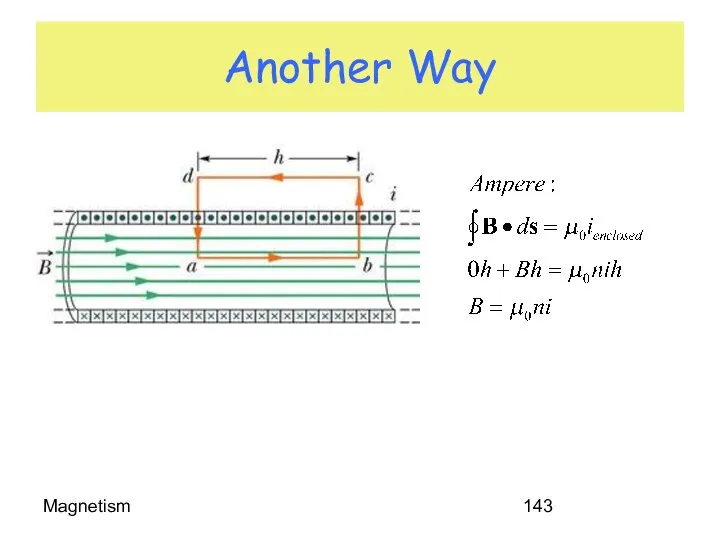
- 143. Magnetism Another Way
- 144. Magnetism Application Creation of Uniform Magnetic Field Region Minimal field outside except at the ends!
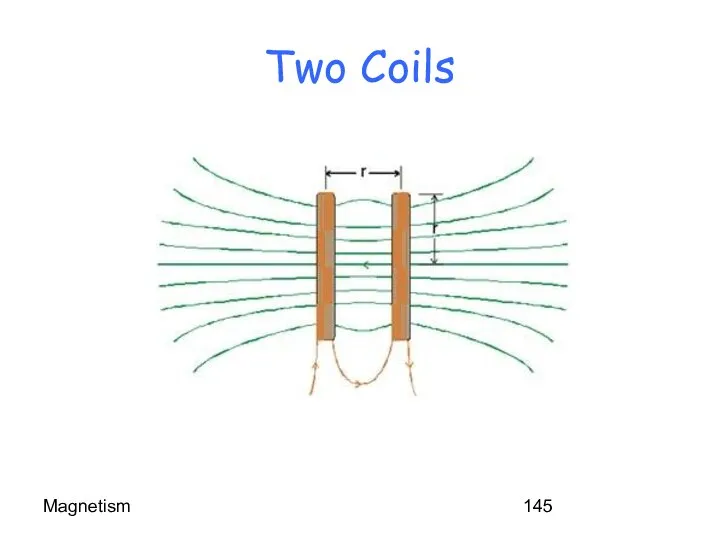
- 145. Magnetism Two Coils
- 146. Magnetism “Real” Helmholtz Coils Used for experiments. Can be aligned to cancel out the Earth’s magnetic
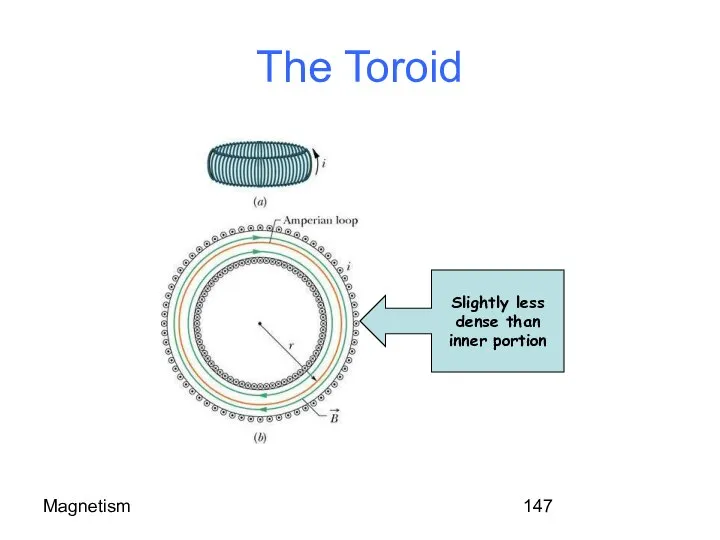
- 147. Magnetism The Toroid Slightly less dense than inner portion
- 149. Скачать презентацию















































































 Презентация по физике "Влажность воздуха" - скачать бесплатно
Презентация по физике "Влажность воздуха" - скачать бесплатно FOURWINGS Дрон нового поколения
FOURWINGS Дрон нового поколения Описание дефектов кристаллической структуры в рамках теории упругости
Описание дефектов кристаллической структуры в рамках теории упругости УРОК ФИЗИКИ В 10 КЛАССЕ Скорости молекул. Опыт Штерна Учитель Кононов Геннадий Григорьевич СОШ № 29 Славянский район
УРОК ФИЗИКИ В 10 КЛАССЕ Скорости молекул. Опыт Штерна Учитель Кононов Геннадий Григорьевич СОШ № 29 Славянский район  Кинетическая энергия
Кинетическая энергия Види та типи генераторів
Види та типи генераторів «Отыщи всему начало и ты многое поймёшь» Кузьма Прутков Брендина Наталья Владимировна Учитель физики МОУ средняя
«Отыщи всему начало и ты многое поймёшь» Кузьма Прутков Брендина Наталья Владимировна Учитель физики МОУ средняя Картография. Геодезические сети и датумы
Картография. Геодезические сети и датумы Сопряжение
Сопряжение Refrigeration Fundamentals. Part 1. Heat and Heat Transfer
Refrigeration Fundamentals. Part 1. Heat and Heat Transfer Движение по окружности
Движение по окружности  Совершенствование организации и технологии ремонта МТП в условиях ОАО Птицефабрика Атемарская
Совершенствование организации и технологии ремонта МТП в условиях ОАО Птицефабрика Атемарская Открытия Ломоносова в области физики
Открытия Ломоносова в области физики Мекемелерді табиғи және жасанды жарықтан деңгейін анықтау
Мекемелерді табиғи және жасанды жарықтан деңгейін анықтау Методы исследования структуры металлов и сплавов
Методы исследования структуры металлов и сплавов Рычаг первого рода
Рычаг первого рода Материалы авиакосмической техники
Материалы авиакосмической техники Ядерные реакции
Ядерные реакции Принцип минимума и смена факторов, лимитирующих рост популяции
Принцип минимума и смена факторов, лимитирующих рост популяции Теория электролитической диссоциации (обобщающий урок)
Теория электролитической диссоциации (обобщающий урок) Сканирлеуші зондтық микроскопия
Сканирлеуші зондтық микроскопия Рентгенівські промені Підготувала Учениця 11-А класу Білоцерківської загальноосвітньої школи І-ІІІ ступенів №
Рентгенівські промені Підготувала Учениця 11-А класу Білоцерківської загальноосвітньої школи І-ІІІ ступенів № Ядерный реактор
Ядерный реактор Презентация по физике "Закон сохранения электрического заряда" - скачать
Презентация по физике "Закон сохранения электрического заряда" - скачать  Виды водного транспорта
Виды водного транспорта Технология термической обработки
Технология термической обработки Механіка. Неінерціальні системи відліку
Механіка. Неінерціальні системи відліку Заземляющие устройства в установках высокого напряжение. (Лекция 17)
Заземляющие устройства в установках высокого напряжение. (Лекция 17)