Содержание
- 2. 1.1 Статистический и термодинамический методы исследования. Статистический метод используется в молекулярной физике. На основе рассмотрения движения
- 3. Макроскопическим параметром называется физическая величина, характеризующая какое-либо свойство системы частиц как целого , например, температура, давление,
- 4. Пример : Как можно получить среднее значение микропараметра. Пусть N раз измеряли скорость молекул газа: Если
- 5. Термодинамический метод исследования не рассматривает внутреннее строение вещества и характер движения отдельных частиц. Термодинамика : --
- 6. 1.2 Состояние системы. Процесс. Макросостояние системы задается набором значений макропараметров (для газов это P,V,T). Микросостояние системы
- 7. Переход системы из одного макроскопического состояния в другое называется процессом, что обязательно связано с нарушением равновесия,
- 8. Равновесный процесс всегда обратим, т.е. может проходить в обратном направлении через те же состояния, что и
- 9. 2. Элементы молекулярно-кинетической теории Основная физическая модель, с которой работает МКТ – идеальный газ. Идеальным газом
- 10. В молекулярной физике естественно при измерении количества вещества исходить из массы одной молекулы -- .
- 11. Уравнение Менделеева – Клапейрона (1) для 1-го моля газа: PV=RT. Универсальная газовая постоянная постоянная Больцмана. Запишем
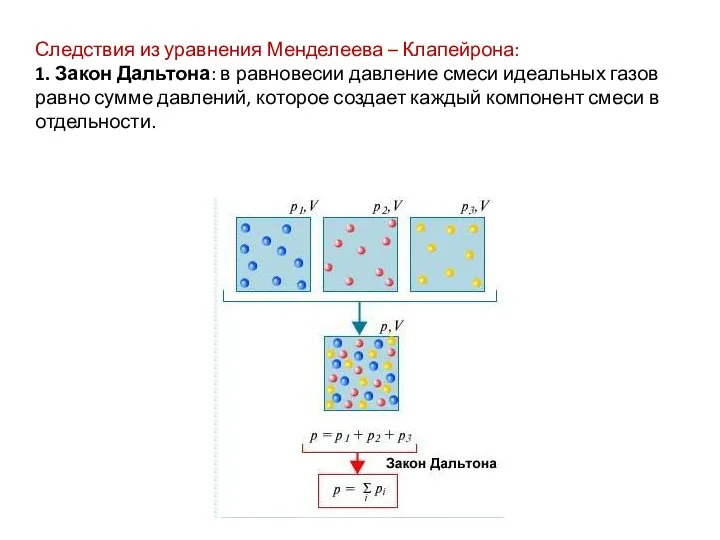
- 12. Следствия из уравнения Менделеева – Клапейрона: 1. Закон Дальтона: в равновесии давление смеси идеальных газов равно
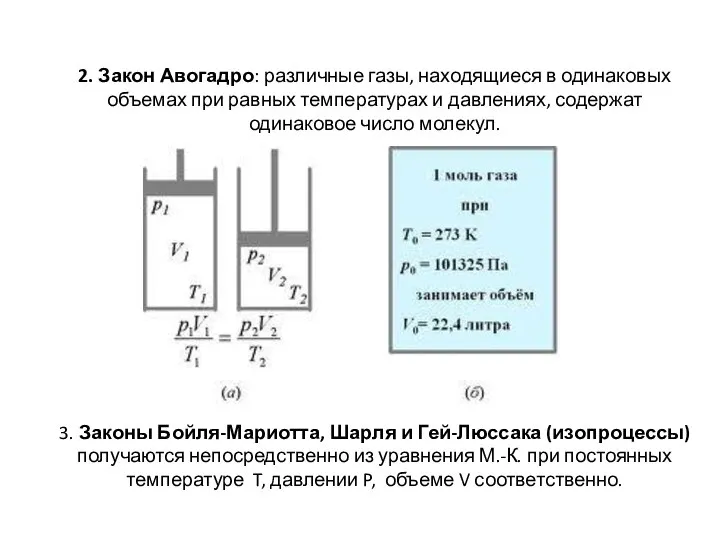
- 13. 2. Закон Авогадро: различные газы, находящиеся в одинаковых объемах при равных температурах и давлениях, содержат одинаковое
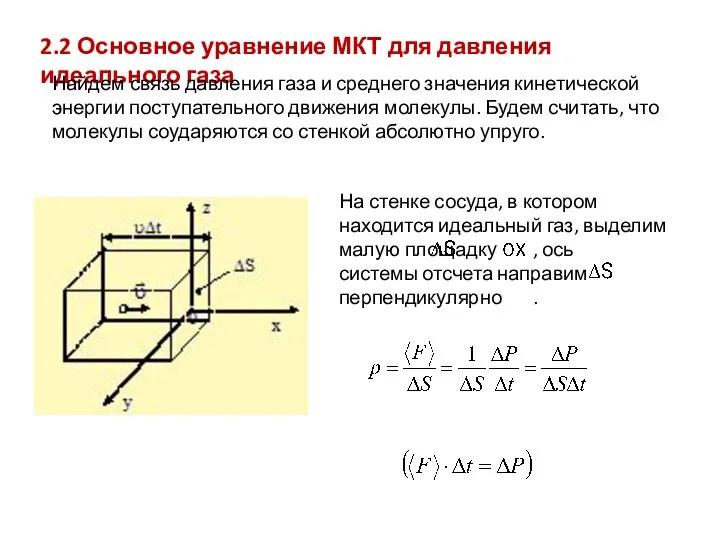
- 14. 2.2 Основное уравнение МКТ для давления идеального газа Найдем связь давления газа и среднего значения кинетической
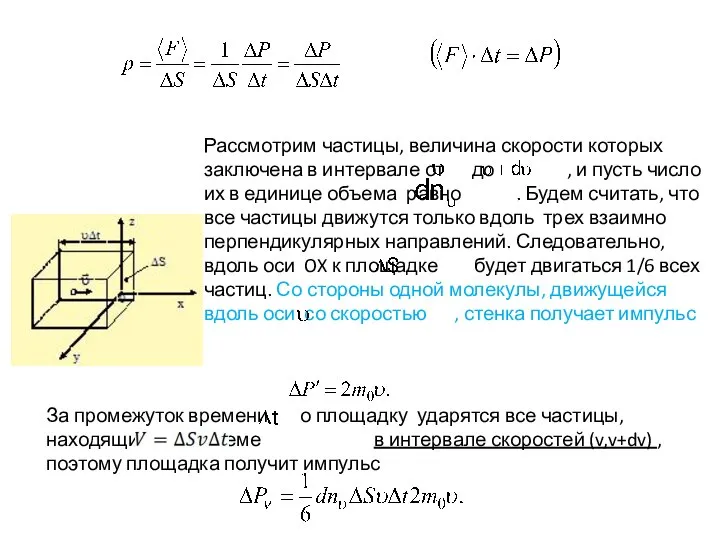
- 15. Рассмотрим частицы, величина скорости которых заключена в интервале от до , и пусть число их в
- 16. Т.к. , то Или: (3) – это основное уравнение МКТ для давления идеального газа. Рассмотрение более
- 17. 2.3 Закон равномерного распределения энергии молекул по степеням свободы Приравняв правые части (1) и (2), получим:
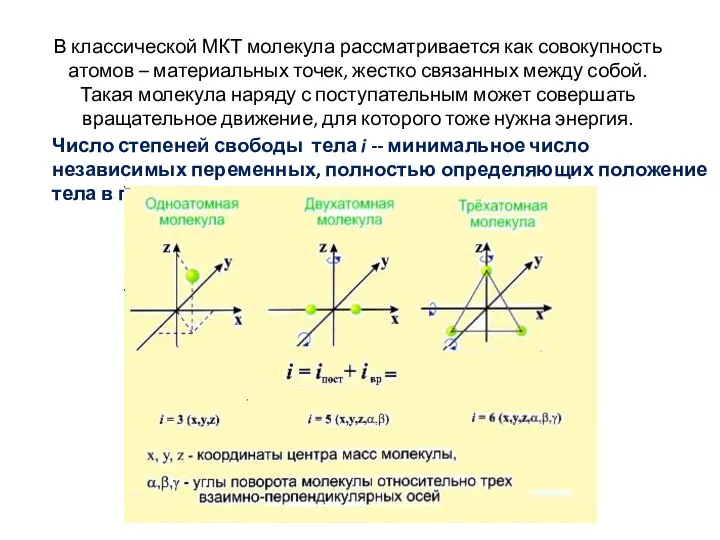
- 18. В классической МКТ молекула рассматривается как совокупность атомов – материальных точек, жестко связанных между собой. Такая
- 19. В статической физике доказывается положение о равномерном распределении энергии по степеням свободы молекулы. На каждую степень
- 20. 3. Статистические законы распределения в МКТ. Статистические законы принципиально отличаются от законов классической механики. Так, закон
- 21. 2. Вероятностью случайного события, дающего результат со значением рi , называется отношение числа испытаний Ni ,
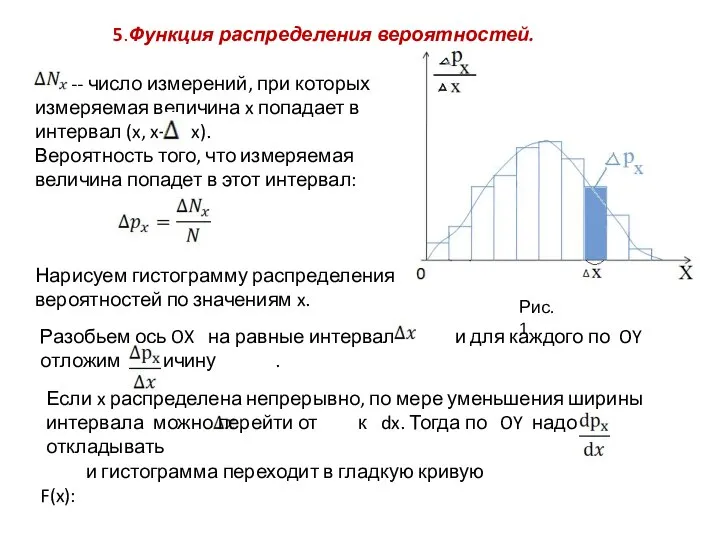
- 22. -- число измерений, при которых измеряемая величина x попадает в интервал (x, x+ x). Вероятность того,
- 23. ) Отсюда -- функция распределения вероятностей появления величины x. Она численно равна относительному числу измерений, которые
- 24. 8. Согласно , среднее значение непрерывно распределенной величины Теперь ее можно выразить через функцию распределения вероятностей:
- 25. Нормальное распределение, также называемое гауссовым распределением или распределением Гаусса — распределение вероятностей, которое играет важнейшую роль
- 26. При приеме в аспирантуру на экзамене часто ставились неразрешимые задачи. Д.Г.Стокс (1819-1903) поставил задачу Максвеллу о
- 27. 3.2 Закон Максвелла для распределения молекул идеального газа по скоростям Поставим задачу об отыскании функции распределения
- 28. Обозначим -- вероятность попадания измеренной скорости молекулы в объем (см. рис.2): Найдем коэффициент пропорциональности из следующих
- 29. В силу равноправия всех направлений в пространстве вид функций должен быть одинаков и отличаться только значениями
- 30. N/j/ aeyrwbz hfcghtltktybz Vfrcdtkkf gj rjvgjytynt crjhjcnb Т.о. функция распределения Максвелла по компоненте скорости имеет экспоненциальный
- 31. Параметр α найдем из следующих соображений. Согласно закону равнораспределения энергии молекулы по степеням свободы , доля
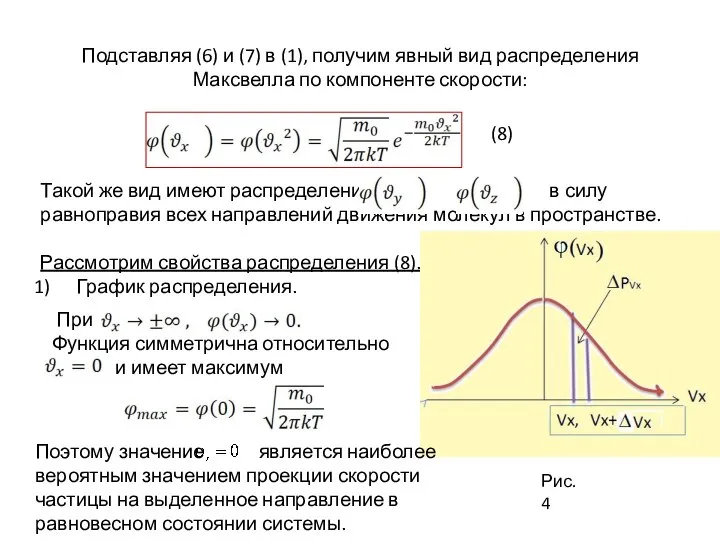
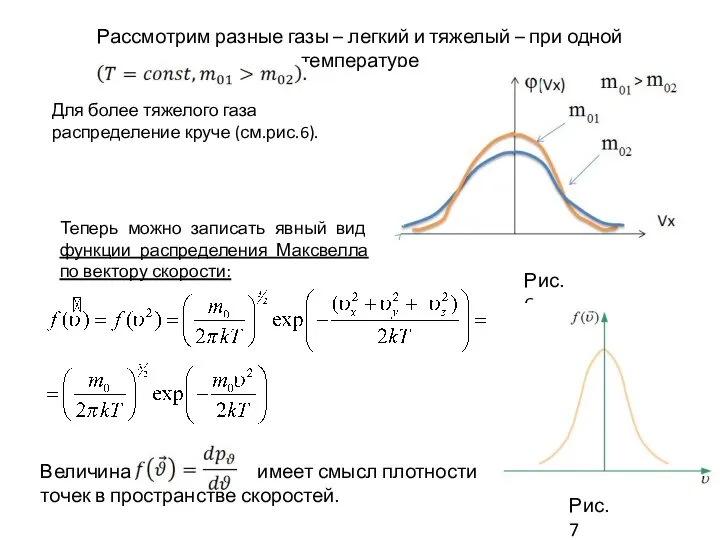
- 32. Подставляя (6) и (7) в (1), получим явный вид распределения Максвелла по компоненте скорости: (8) Такой
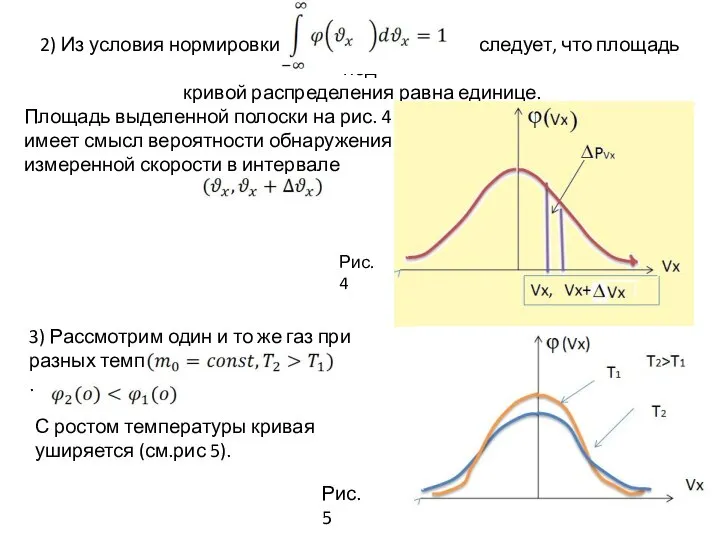
- 33. 2) Из условия нормировки следует, что площадь под кривой распределения равна единице. Площадь выделенной полоски на
- 34. Рассмотрим разные газы – легкий и тяжелый – при одной температуре Рис.6 Для более тяжелого газа
- 35. 3.2.2 Распределение Максвелла по абсолютному значению скорости В пространстве скоростей (рис.8) концы всех векторов, имеющих одно
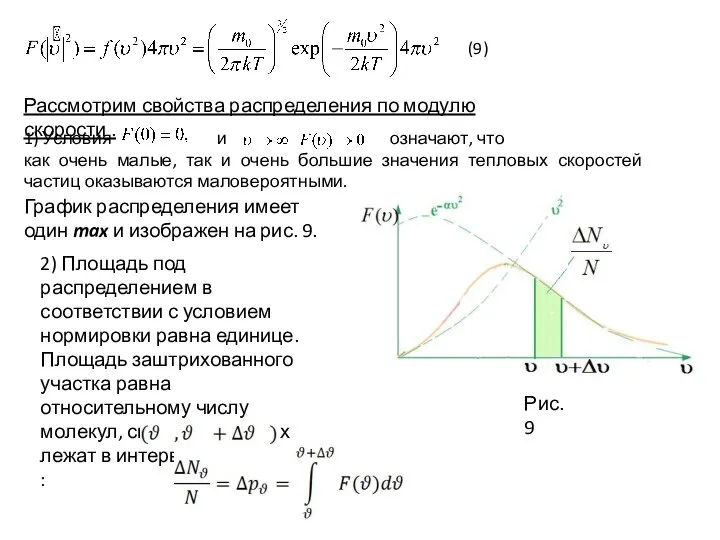
- 36. Рассмотрим свойства распределения по модулю скорости . 1) Условия и означают, что как очень малые, так
- 37. 3) Характерные скорости молекул газа. Наиболее вероятная скорость соответствует максимуму распределения по модулю скорости (см.рис.10) и
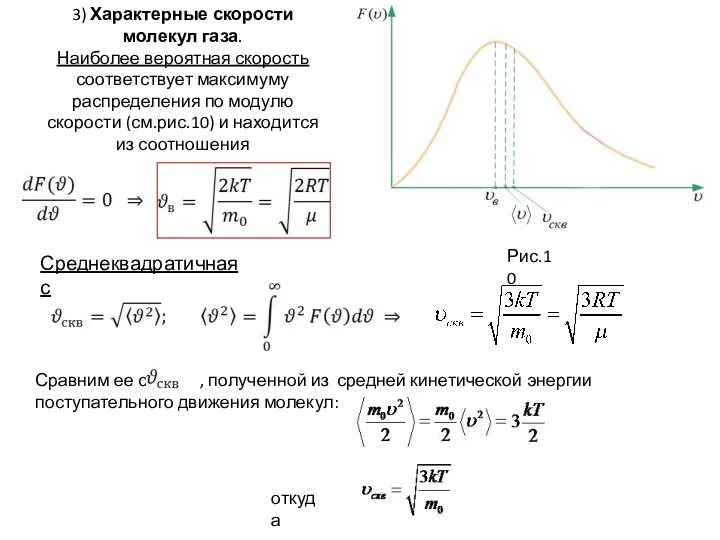
- 38. Средняя арифметическая скорость 4)
- 40. Распределение Максвелла по модулю скорости можно преобразовать в распределение частиц по значениям кинетической энергии поступательного движения
- 41. 3.3.1 Барометрическая формула 3.3 Газы в силовом поле В состоянии равновесия при отсутствии внешних силовых полей
- 42. Выражая плотность из уравнения Менделеева-Клапейрона и подставляя её в (1), получим (2). Интегрирование приводит к соотношению
- 43. Барометрическую формулу (5) можно записать в другом виде, используя связь , где - масса одной молекулы
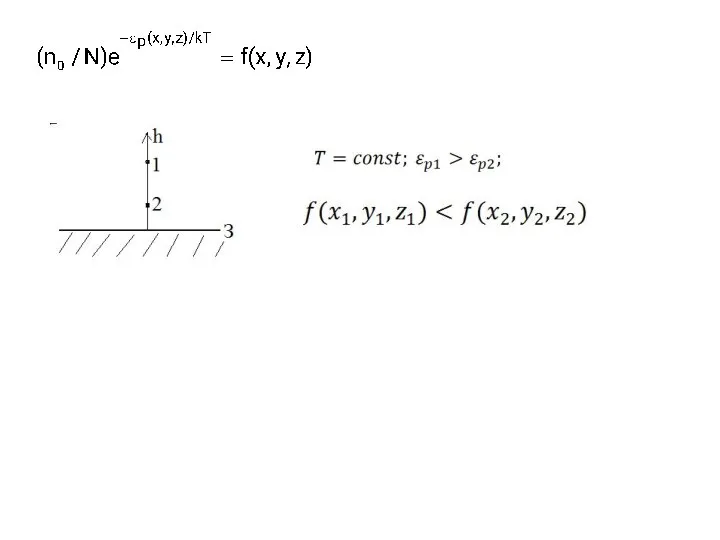
- 44. 3.3.2 РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА Нетрудно заметить, что в соотношении (6) выражение в показателе экспоненты является потенциальной энергией
- 45. Cледует, однако, помнить, что размеры элементарного объема не могут быть сколь угодно малыми. Этот объем должен
- 47. Поскольку распределения Максвелла и Больцмана статистически независимы, то вероятность обнаружить частицу, обладающую скоростью из интервала .
- 49. Скачать презентацию

































 Выдувание пузырей
Выдувание пузырей Физика конденсированного состояния. Движение электронов в атоме
Физика конденсированного состояния. Движение электронов в атоме Лекция 12 Тема:Уравнение состояния идеального газа .
Лекция 12 Тема:Уравнение состояния идеального газа .  Основные © В.Е. Фрадкин, 2004
Основные © В.Е. Фрадкин, 2004 Расчет установившихся режимов простейших электрических сетей. (Глава 6)
Расчет установившихся режимов простейших электрических сетей. (Глава 6) Выполнила: Ученица 4 «э» класса Худобина Елизавета Руководитель: О. И. Баранцева (программа XXI 4 классов) г. Санкт-Петербург 2011 год.
Выполнила: Ученица 4 «э» класса Худобина Елизавета Руководитель: О. И. Баранцева (программа XXI 4 классов) г. Санкт-Петербург 2011 год. Интерференция света 11 класс
Интерференция света 11 класс  Проект «В царстве Архимеда»
Проект «В царстве Архимеда» Механическое движение
Механическое движение Исследовательский проект «Машина Голдберга и бизиборд «Кваторианский домик»
Исследовательский проект «Машина Голдберга и бизиборд «Кваторианский домик» Дифракция света. Принцип Гюйгенса-Френеля
Дифракция света. Принцип Гюйгенса-Френеля Презентация к уроку в 7 классе по теме: «Сила» Учитель физики первой квалификационной категории МБОУ «Россошинская сош»
Презентация к уроку в 7 классе по теме: «Сила» Учитель физики первой квалификационной категории МБОУ «Россошинская сош»  Основы кинематики
Основы кинематики Презентация по физике "Производство, передача и потребление электроэнергии" - скачать
Презентация по физике "Производство, передача и потребление электроэнергии" - скачать  Открытие В.К. Рентгеном Х-лучей. Открытие А. Беккерелем явления радиоактивности
Открытие В.К. Рентгеном Х-лучей. Открытие А. Беккерелем явления радиоактивности Математическое моделирование как основной метод изучения процессов и решения задач оптимизации и управления в биосфере
Математическое моделирование как основной метод изучения процессов и решения задач оптимизации и управления в биосфере Плавление и отвердевание кристаллических тел
Плавление и отвердевание кристаллических тел Диэлектрофорез вирионов осповакцины
Диэлектрофорез вирионов осповакцины ВІльям Томсон
ВІльям Томсон Аттестационная работа. Равновесие рычага и золотое сечение
Аттестационная работа. Равновесие рычага и золотое сечение Поток энергии и цепи питания Автор презентации = учитель биологии ГБОУ СОШ№113 Архипова Татьяна Сергеевна
Поток энергии и цепи питания Автор презентации = учитель биологии ГБОУ СОШ№113 Архипова Татьяна Сергеевна Тяговые расчеты при проектировании железной дороги
Тяговые расчеты при проектировании железной дороги Форма и ширина спектральной линии
Форма и ширина спектральной линии Процессы обработки влажного воздуха
Процессы обработки влажного воздуха Деление тяжелых ядер. Цепная ядерная реакция. Ядерный реактор. Ядерная энергетика
Деление тяжелых ядер. Цепная ядерная реакция. Ядерный реактор. Ядерная энергетика Презентация на тему: Выполнила работу: Хамедова Хасиба 10 класса «А»
Презентация на тему: Выполнила работу: Хамедова Хасиба 10 класса «А»  Явление молнии
Явление молнии  Модели на основе ДУ в частных производных и метод конечных разностей
Модели на основе ДУ в частных производных и метод конечных разностей