Содержание
- 2. 1. Понятие о неинерциальных системах отсчёта В предыдущих разделах рассматривался и использовался лишь класс инерциальных систем
- 3. 1. Понятие о неинерциальных системах отсчёта Если радиус-вектор частицы в системе К обозначить , то в
- 4. Из рисунка видно, что радиусы-векторы частицы т в инерциальной ( ) и неинерциальной ( ) системах
- 5. Основное свойство неинерциальных систем состоит в том, что в этих системах существуют поля ускорений. Закон Ньютона
- 6. 2. Силы инерции Силы инерции – это силы, обусловленные ускоренным движением системы отсчета, относительно измеряемой системы
- 7. 2. Силы инерции Виды сил инерции и их проявления 1. Силы инерции при ускоренном поступательном движении
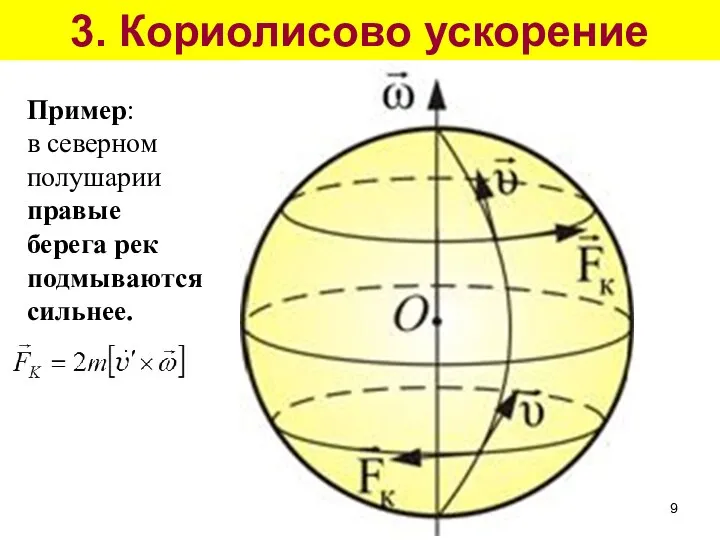
- 8. 3. Кориолисово ускорение
- 9. 3. Кориолисово ускорение Пример: в северном полушарии правые берега рек подмываются сильнее.
- 10. 2.3. Кориолисово ускорение
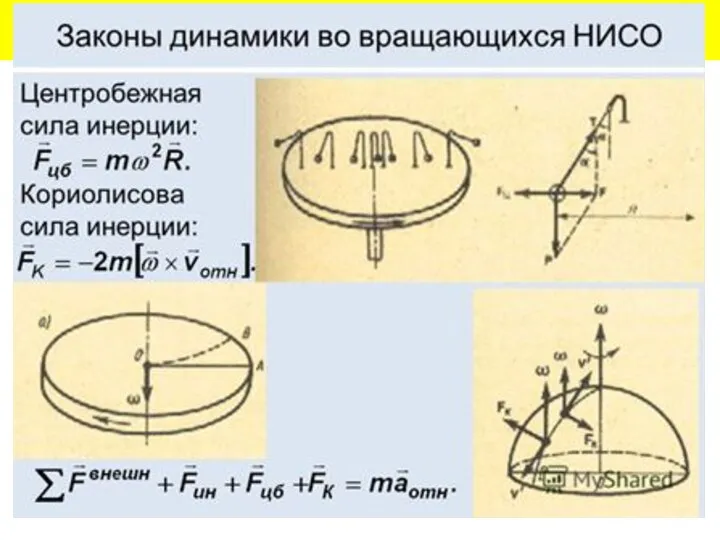
- 11. Основной закон динамики для неинерциальных систем отсчёта (НИСО) _ _ _ _ _ Далее – интернет-тесты
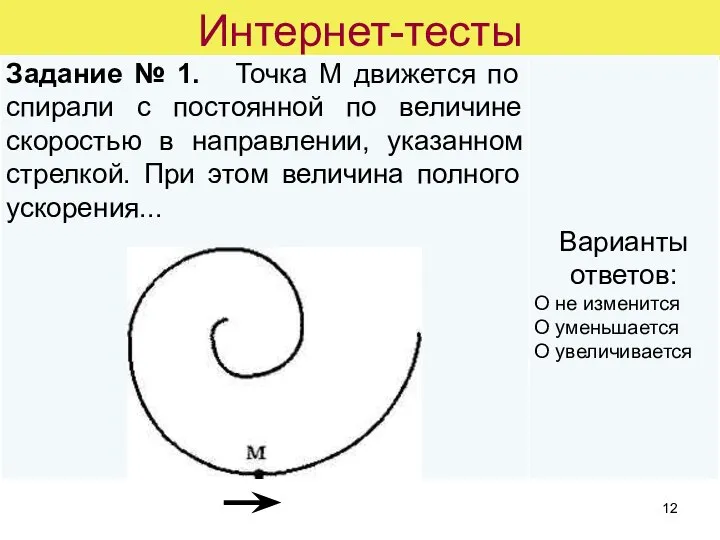
- 12. Интернет-тесты
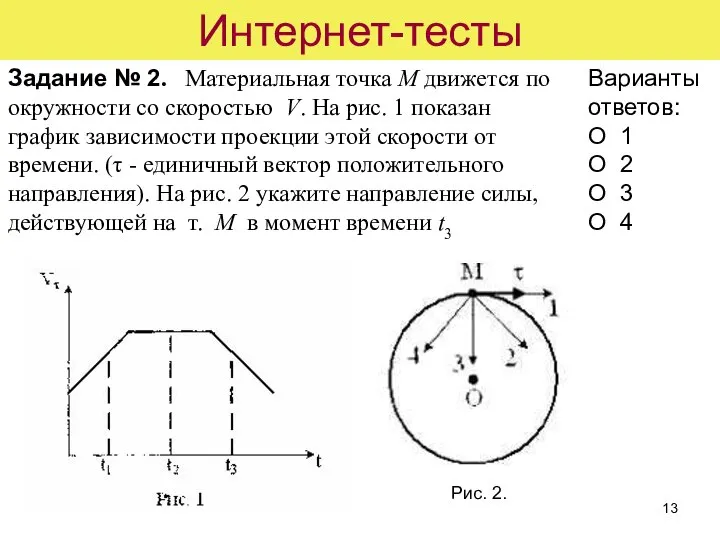
- 13. Интернет-тесты Задание № 2. Материальная точка М движется по окружности со скоростью V. На рис. 1
- 14. Интернет-тесты Задание № 3. Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением ,
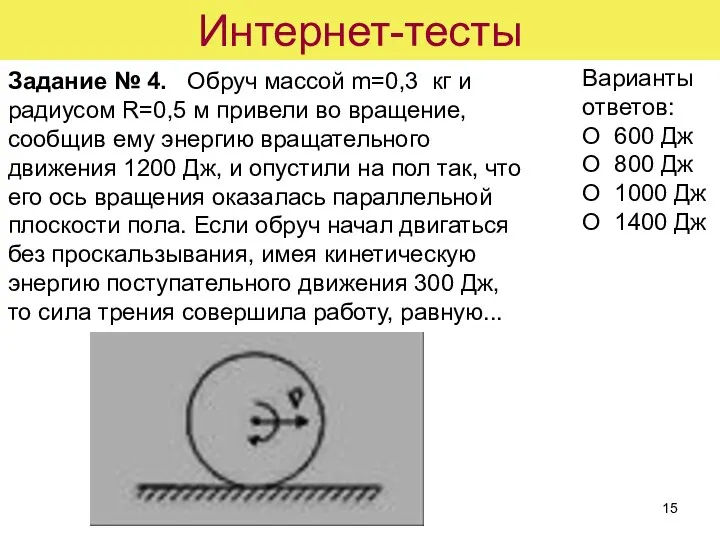
- 15. Интернет-тесты Задание № 4. Обруч массой m=0,3 кг и радиусом R=0,5 м привели во вращение, сообщив
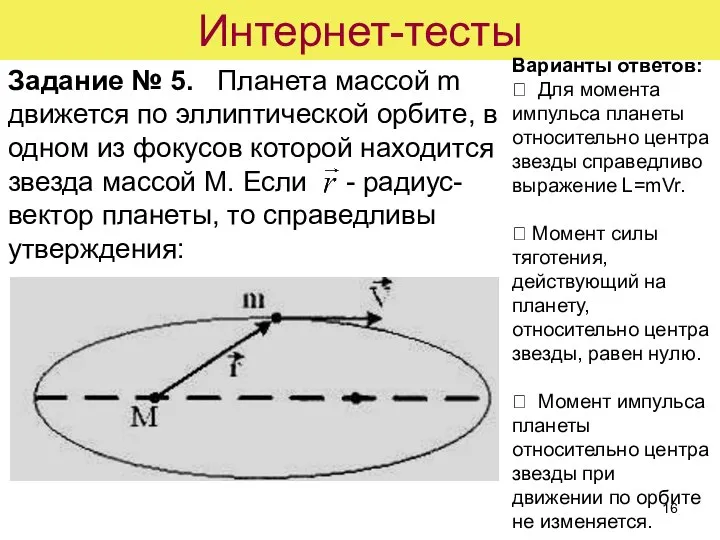
- 16. Интернет-тесты Задание № 5. Планета массой m движется по эллиптической орбите, в одном из фокусов которой
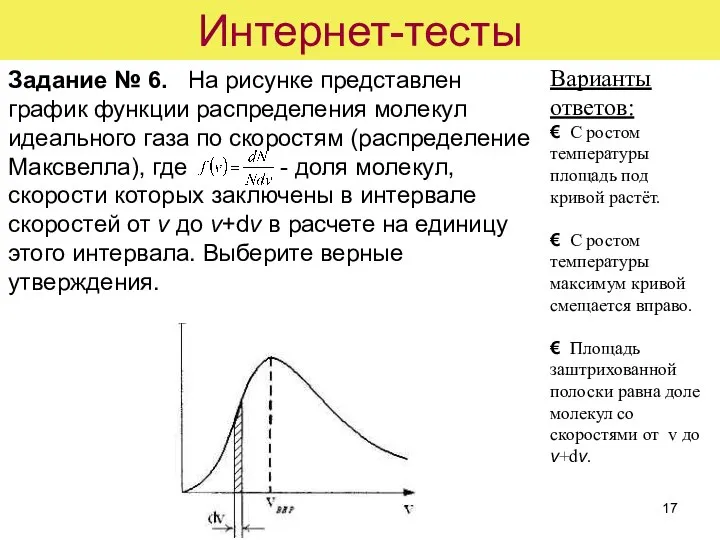
- 17. Интернет-тесты Задание № 6. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение
- 18. Интернет-тесты
- 20. Скачать презентацию










 Система с использованием ПИД-регулятора для задачи следования по линии
Система с использованием ПИД-регулятора для задачи следования по линии Поляризация света. Применение
Поляризация света. Применение Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Аттестационная работа. Методическя разработка по физике: «Замена человека на производстве роботизированный манипулятор»
Аттестационная работа. Методическя разработка по физике: «Замена человека на производстве роботизированный манипулятор» Физика. Введение в предмет
Физика. Введение в предмет Теплообмен излучением (часть 2)
Теплообмен излучением (часть 2) Презентация по физике "Атомные элэктростанции" - скачать
Презентация по физике "Атомные элэктростанции" - скачать  Коррозия металлов. (Лекция 7)
Коррозия металлов. (Лекция 7) Экспериментальная аэродинамика
Экспериментальная аэродинамика Изготовление модели двигателя Стирлинга
Изготовление модели двигателя Стирлинга Газотурбинные двигатели
Газотурбинные двигатели ІІ закон термодинаміки
ІІ закон термодинаміки  Свет и цвета тел
Свет и цвета тел Энергетический подход
Энергетический подход Плоская и пространственная система сил
Плоская и пространственная система сил Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Презентация по физике "Одинокие атомы" - скачать
Презентация по физике "Одинокие атомы" - скачать  Перемещение, путь, траектория
Перемещение, путь, траектория Доминик Франсуа АРАГО © В.Е. Фрадкин, СПб АППО - РГПУ, 2007-08
Доминик Франсуа АРАГО © В.Е. Фрадкин, СПб АППО - РГПУ, 2007-08 История изобретения и развития тепловых двигателей Корнева Н.А. Учитель физики МОУ «Гимназия №5»
История изобретения и развития тепловых двигателей Корнева Н.А. Учитель физики МОУ «Гимназия №5» Полевая геофизика. Сейсморазведка
Полевая геофизика. Сейсморазведка Тест 2 - 2011. Квантовая теория
Тест 2 - 2011. Квантовая теория Использование солнечной энергии
Использование солнечной энергии Агрегатные состояния вещества. Плавление и кристаллизация Максим Иванов 8 класс «А» ГОУ СОШ №1266 г. Москва Январь, 2009
Агрегатные состояния вещества. Плавление и кристаллизация Максим Иванов 8 класс «А» ГОУ СОШ №1266 г. Москва Январь, 2009  Презентация по физике "Ф.А Бредихин" - скачать бесплатно
Презентация по физике "Ф.А Бредихин" - скачать бесплатно Презентация по физике "Какие электроприборы есть на кухне?" - скачать бесплатно
Презентация по физике "Какие электроприборы есть на кухне?" - скачать бесплатно Тележки нового поколения
Тележки нового поколения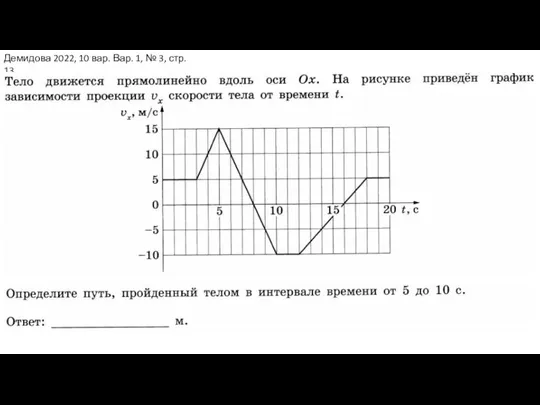 Механика. Демидова 2022, 10 вар. Вар. 1, № 3, стр. 13
Механика. Демидова 2022, 10 вар. Вар. 1, № 3, стр. 13