Содержание
- 2. Lecture 4 Rotation of rigid bodies. Angular momentum and torque. Properties of fluids. Flotation. Bernulli equation.
- 3. Rotation of Rigid Bodies When a rigid object is rotating about a fixed axis, every particle
- 4. Radians
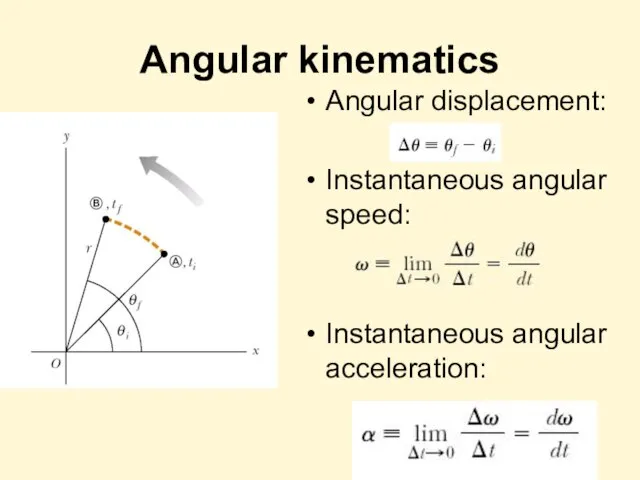
- 5. Angular kinematics Angular displacement: Instantaneous angular speed: Instantaneous angular acceleration:
- 6. Angular and linear quantities Every particle of the object moves in a circle whose center is
- 7. Total linear acceleration Tangential acceleration is perpendicular to the centripetal one, so the magnitude of total
- 8. Angular velocity Angular velocity is a vector. The right hand rule is applied: If the fingers
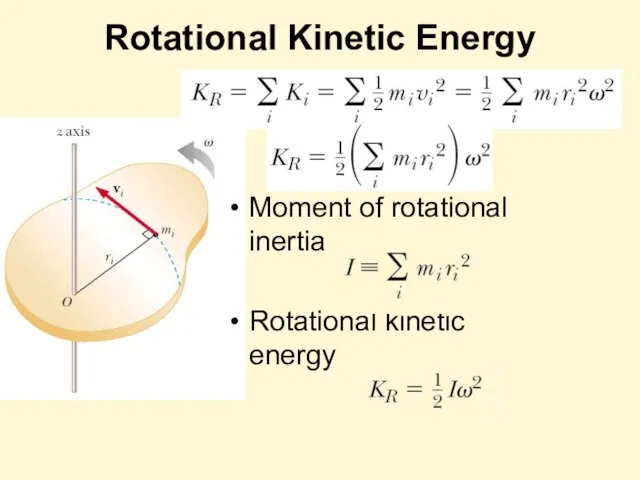
- 9. Rotational Kinetic Energy Moment of rotational inertia Rotational kinetic energy
- 10. Calculations of Moments of Inertia
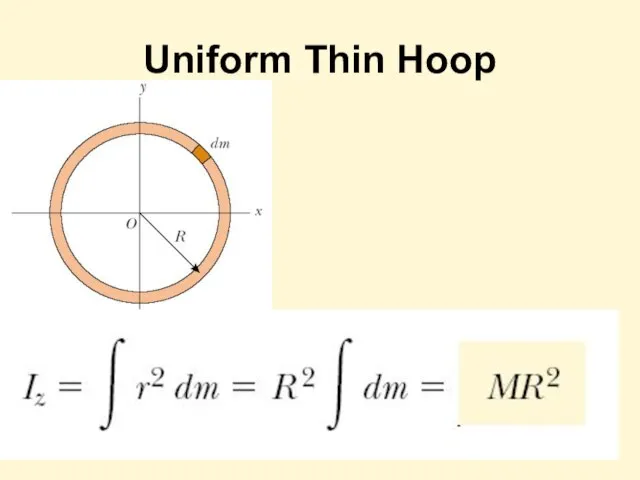
- 11. Uniform Thin Hoop
- 12. Uniform Rigid Rod
- 13. Uniform Solid Cylinder
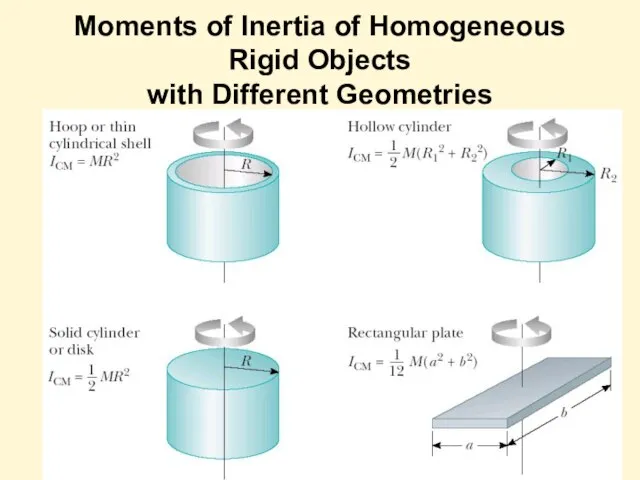
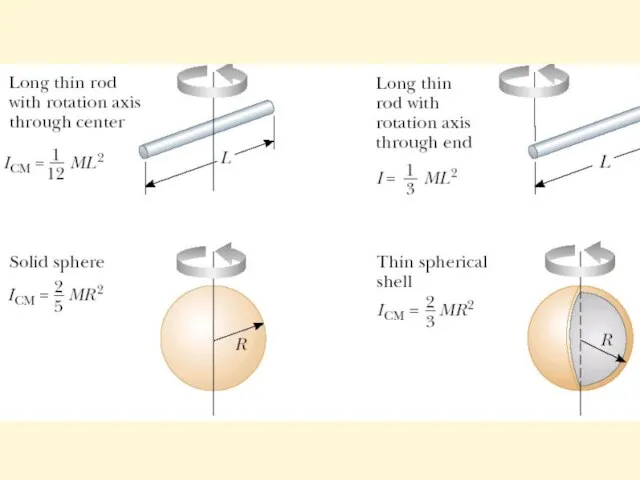
- 14. Moments of Inertia of Homogeneous Rigid Objects with Different Geometries
- 16. Parallel-axis theorem Suppose the moment of inertia about an axis through the center of mass of
- 18. Torque When a force is exerted on a rigid object pivoted about an axis, the object
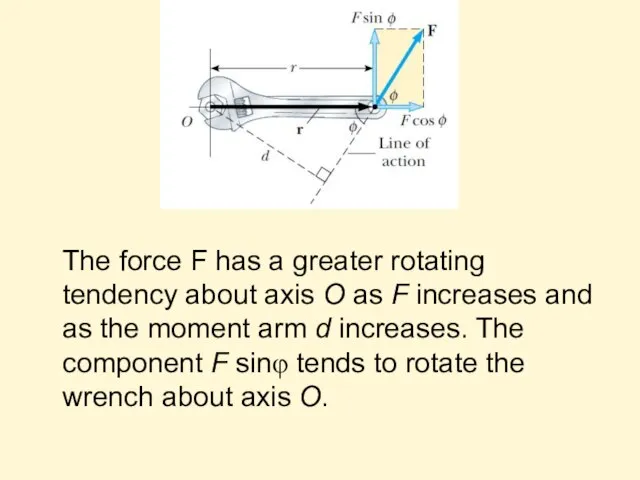
- 19. The force F has a greater rotating tendency about axis O as F increases and as
- 20. The force F1 tends to rotate the object counterclockwise about O, and F2 tends to rotate
- 21. Torque is not Force Torque is not Work Torque should not be confused with force. Forces
- 22. Rotational Dynamics Let’s add which equals zero, as and are parallel. Then: So we get
- 23. Rotational analogue of Newton’s second law Quantity L is an instantaneous angular momentum. The torque acting
- 24. Net External Torque The net external torque acting on a system about some axis passing through
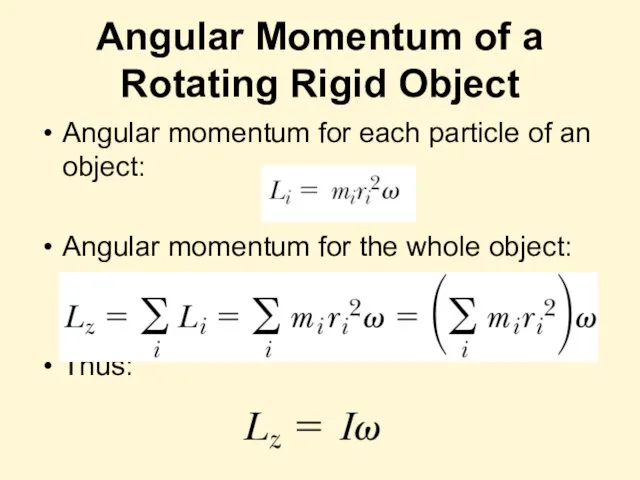
- 25. Angular Momentum of a Rotating Rigid Object Angular momentum for each particle of an object: Angular
- 26. Angular acceleration
- 27. The Law of Angular Momentum Conservation The total angular momentum of a system is constant if
- 28. Change in internal structure of a rotating body can result in change of its angular velocity.
- 29. When a rotating skater pulls his hands towards his body he spins faster.
- 30. Three Laws of Conservation for an Isolated System Full mechanical energy, linear momentum and angular momentum
- 31. Work-Kinetic Theory for Rotations Similarly to linear motion:
- 32. The net work done by external forces in rotating a symmetric rigid object about a fixed
- 33. Equations for Rotational and Linear Motions
- 34. Gyroscope One typical type of gyroscope is made by suspending a relatively massive rotor inside three
- 35. At high speeds, the gyroscope exhibits extraordinary stability of balance and maintains the direction of the
- 36. If a gyroscope is tipped, the gimbals will try to reorient to keep the spin axis
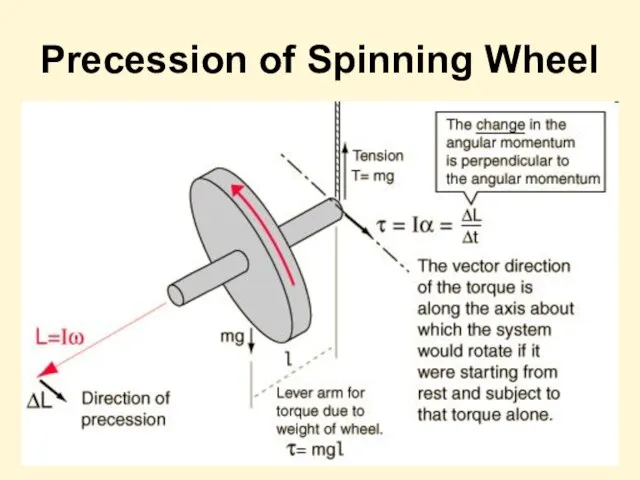
- 37. Precession of Spinning Wheel
- 38. Fluids and liquids
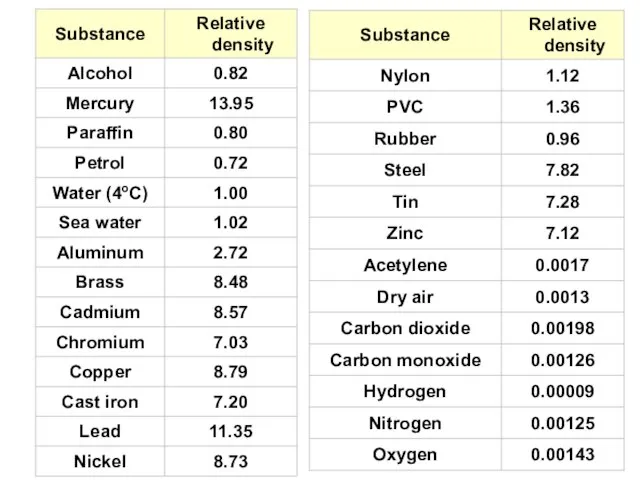
- 39. Relative density Relative density or specific gravity is the ratio of the density of a substance
- 41. Specific volume of a substance is the ratio of the substance's volume to its mass. It
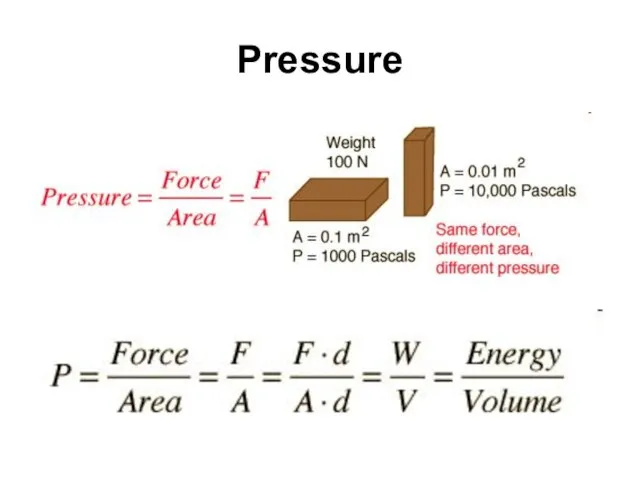
- 42. Pressure
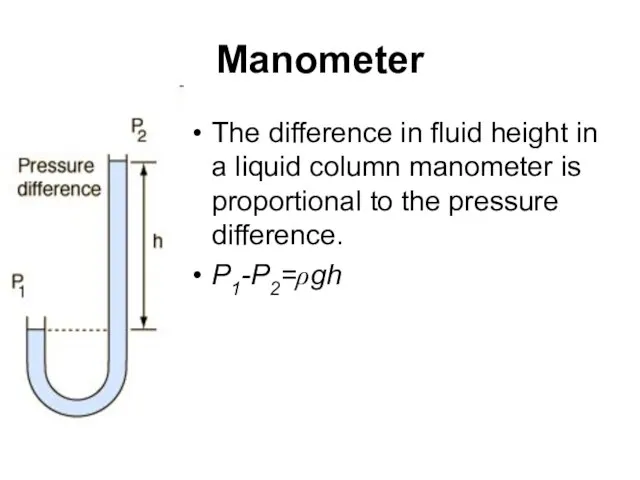
- 43. Manometer The difference in fluid height in a liquid column manometer is proportional to the pressure
- 44. Static Fluid Pressure Pstatic fluid = ρgh where ρ = m/V = fluid density g =
- 45. Pressure Thrust Thrust is a total force in a particular direction. The unit of thrust, therefore
- 46. Atmospheric Pressure The surface of the earth is at the bottom of an atmospheric sea. The
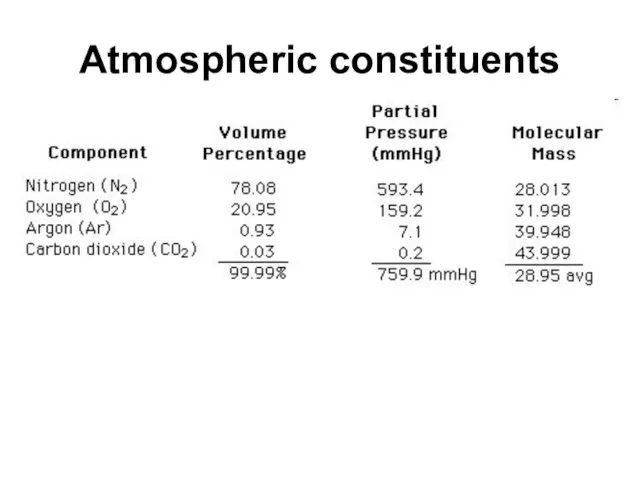
- 47. Atmospheric constituents
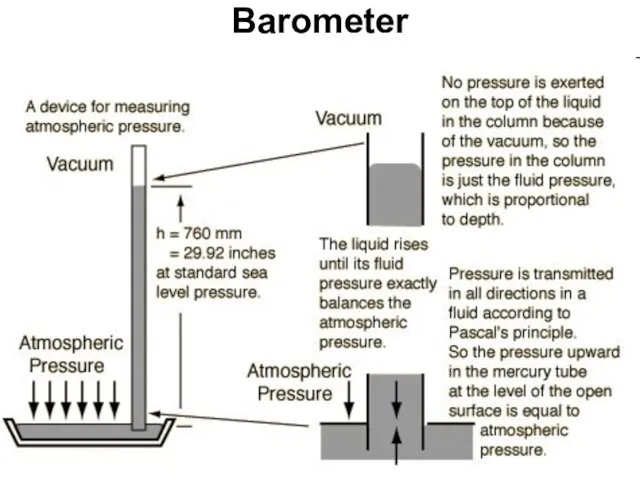
- 48. Barometer
- 49. Aneroid barometer An aneroid barometeru ses a small, flexible metal box called an aneroid cell (capsule),
- 51. The Barometric Formula μair=28.9644 g/mol mair= μair/Na
- 52. Pascal's Principle Pressure exerted anywhere in a confined incompressible fluid is transmitted equally in all directions
- 54. Hydraulic Press
- 55. Lift pump The lift pump, also known as a suction pump, operates as follows: on the
- 56. Force pump The force pump, also known as a pressure pump, operates as follows: on the
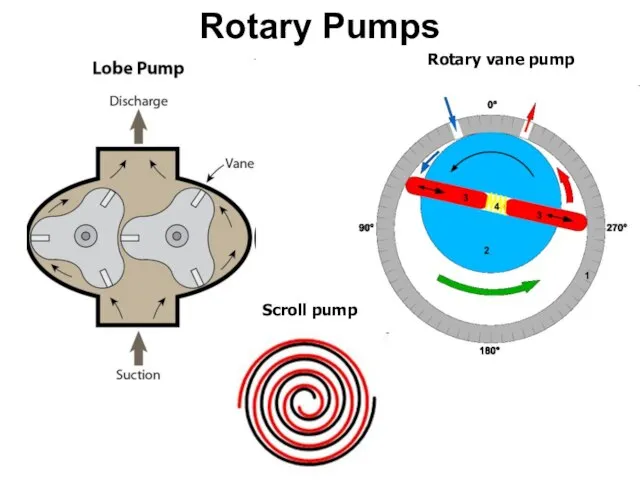
- 57. Rotary Pumps Rotary vane pump Scroll pump
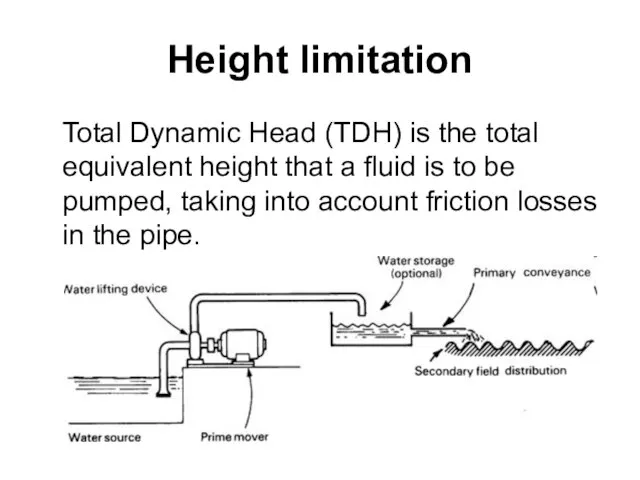
- 58. Height limitation Total Dynamic Head (TDH) is the total equivalent height that a fluid is to
- 59. Total Dynamic Height TDH = Static Height + Static Lift + Friction Loss Static Height is
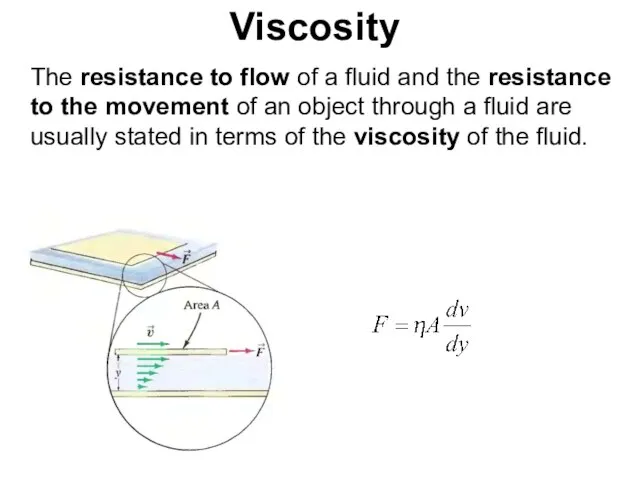
- 60. Viscosity The resistance to flow of a fluid and the resistance to the movement of an
- 61. Experimentally, under conditions of laminar flow, the force required to move a plate at constant speed
- 63. Drag force due viscosity In a viscous fluid, a boundary layer is formed. This causes a
- 64. Effect of Temperature on Viscosity The temperature dependence of liquid viscosity is the phenomenon by which
- 65. Liquid Damping Damping is an effect that reduces the amplitude of oscillations in an oscillatory system
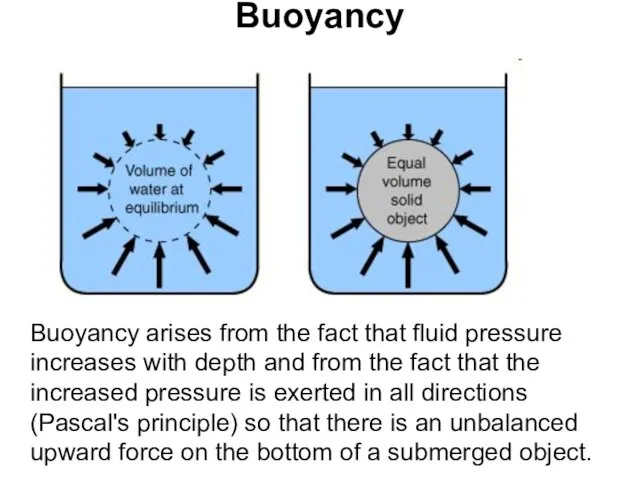
- 68. Buoyancy Buoyancy arises from the fact that fluid pressure increases with depth and from the fact
- 69. Archimedes' Principle The buoyant force on a submerged object is equal to the weight of the
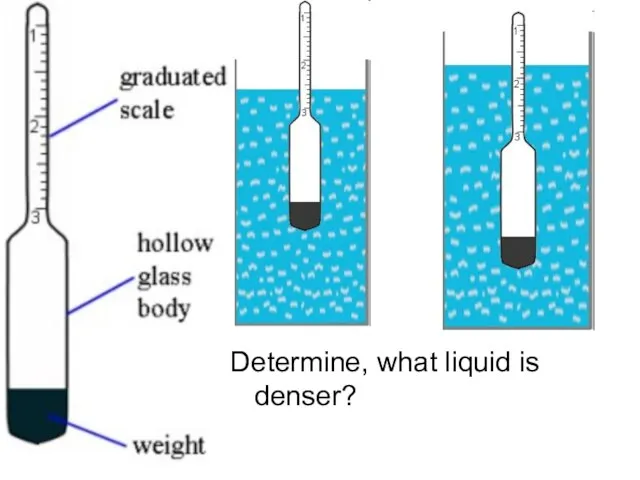
- 70. Hydrometer A hydrometer is an instrument used to measure the specific gravity (or relative density) of
- 72. Determine, what liquid is denser?
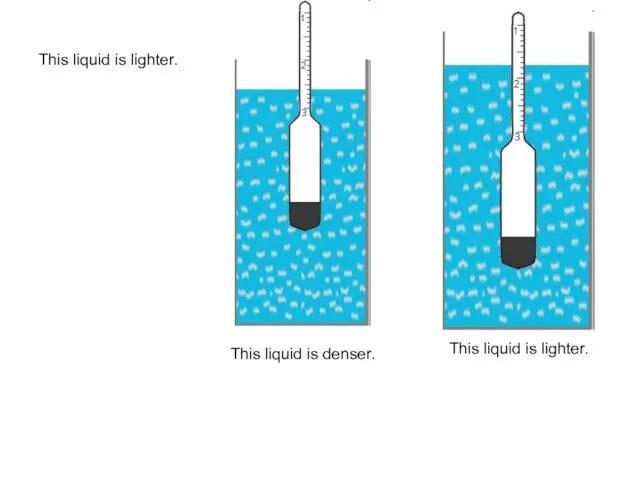
- 73. This liquid is lighter. This liquid is denser. This liquid is lighter.
- 74. Fluid Kinetic Energy The kinetic energy of a moving fluid is more useful in applications like
- 75. Fluid Potential Energy The potential energy of a moving fluid is more useful in applications like
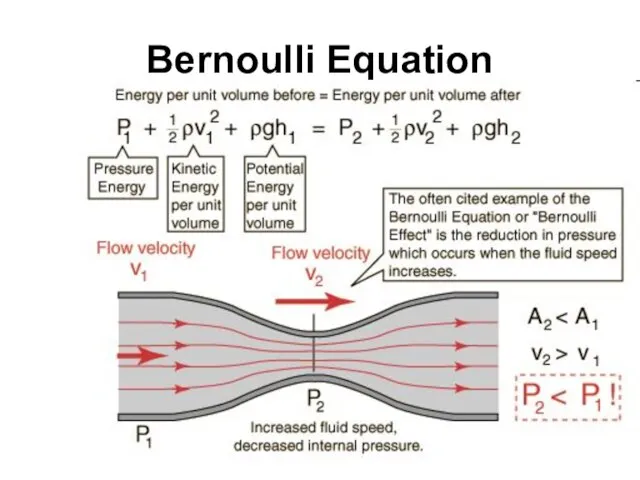
- 76. Bernoulli Equation
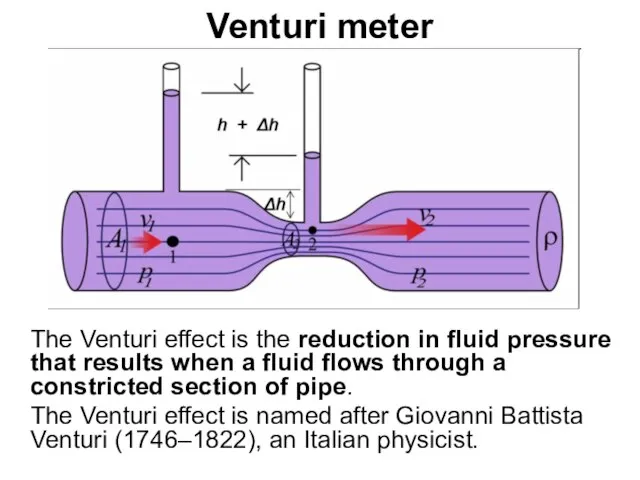
- 77. Venturi meter The Venturi effect is the reduction in fluid pressure that results when a fluid
- 78. Venturi effect Q is volumetric flow rate So Venturi meter can be used to measure the
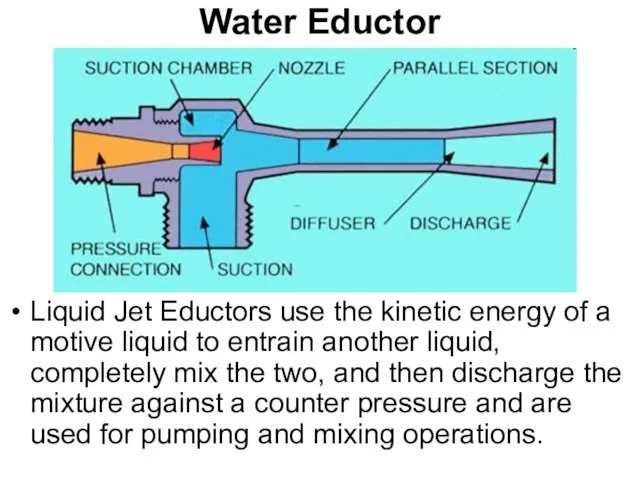
- 79. Water Eductor Liquid Jet Eductors use the kinetic energy of a motive liquid to entrain another
- 82. Скачать презентацию

























































 Терморезистор
Терморезистор Конденсатор. Емкость конденсатора. Энергия электрического поля конденсатора
Конденсатор. Емкость конденсатора. Энергия электрического поля конденсатора Аналогии физических свойств сегнетоэлектрических и ферромагнитных кристаллов
Аналогии физических свойств сегнетоэлектрических и ферромагнитных кристаллов Особенности размещения электронов по орбиталям в атомах малых и больших периодов
Особенности размещения электронов по орбиталям в атомах малых и больших периодов Внутренняя энергия и работа в термодинамике
Внутренняя энергия и работа в термодинамике Презентация по физике Три состояния вещества Физика 7 класс
Презентация по физике Три состояния вещества Физика 7 класс  Кипение Выполнила Шумская О.В. ГБОУ СОШ №201
Кипение Выполнила Шумская О.В. ГБОУ СОШ №201 УРОК ФИЗИКИ В 10 КЛАССЕ Лабораторная работа №3 «Опытная проверка закона Гей – Люссака» Учитель Кононов Геннадий
УРОК ФИЗИКИ В 10 КЛАССЕ Лабораторная работа №3 «Опытная проверка закона Гей – Люссака» Учитель Кононов Геннадий  Петрофизика в свете геофизики
Петрофизика в свете геофизики Рисунки к газовым смесям
Рисунки к газовым смесям Физические и химические явления
Физические и химические явления Экономия электрической энергии и использование энергоэффективных ламп
Экономия электрической энергии и использование энергоэффективных ламп Яблоко Ньютона и подлинная история открытия закона всемирного тяготения
Яблоко Ньютона и подлинная история открытия закона всемирного тяготения Колебания-1. Гармоническое колебание и его характеристики. Модель гармонического осциллятора
Колебания-1. Гармоническое колебание и его характеристики. Модель гармонического осциллятора Строение атома. Урок №7
Строение атома. Урок №7 Индукционные и высокочастотные установки
Индукционные и высокочастотные установки Интенсивность звука в идеальной жидкости
Интенсивность звука в идеальной жидкости Кинематический анализ
Кинематический анализ Электромагнитная картина мира (ЭМКМ). Специальная и общая теории относительности
Электромагнитная картина мира (ЭМКМ). Специальная и общая теории относительности Облака
Облака Основні визначення. Характеристики надійності об'єкта
Основні визначення. Характеристики надійності об'єкта Основы классической теории электропроводности металлов
Основы классической теории электропроводности металлов Измерение параметров лазерного излучения
Измерение параметров лазерного излучения Изучение основных электрофизических характеристик полупроводника
Изучение основных электрофизических характеристик полупроводника Проекитрование и производство изделий интегральной электроники. Диффузия примесей
Проекитрование и производство изделий интегральной электроники. Диффузия примесей Аналіз контрольної роботи № 1. Механічна взаємодія тіл. Сила. Види сил у механіці
Аналіз контрольної роботи № 1. Механічна взаємодія тіл. Сила. Види сил у механіці Перенапряжения в отключении малых индуктивных токов. (Лекция 2.3)
Перенапряжения в отключении малых индуктивных токов. (Лекция 2.3) Введение в физику. (Лекция 1)
Введение в физику. (Лекция 1)