Содержание
- 2. Колебания – процессы, отличающиеся повторяемостью. В зависимости от природы бывают: механическими, электромагнитными, электромеханическими. Механическими колебаниями называются
- 3. Рассмотрим систему, состоящую из шарика подвешенного на пружине. В состоянии равновесия- сила тяжести уравновешивается силой упругости:
- 4. Уравнение второго закона Ньютона для шарика: Обозначим и получим: Движение шарика под действием силы описывается линейным
- 5. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f (t).
- 6. Смещение: Скорость: Ускорение: Ускорение и смещение в противофазе! Кинетическая энергия равна: Потенциальная энергия равна: Полная энергия:
- 7. Систему, описываемую уравнением: где w02- постоянная положительная величина, называют гармоническим осциллятором. Решение имеет вид: Гармонический осциллятор
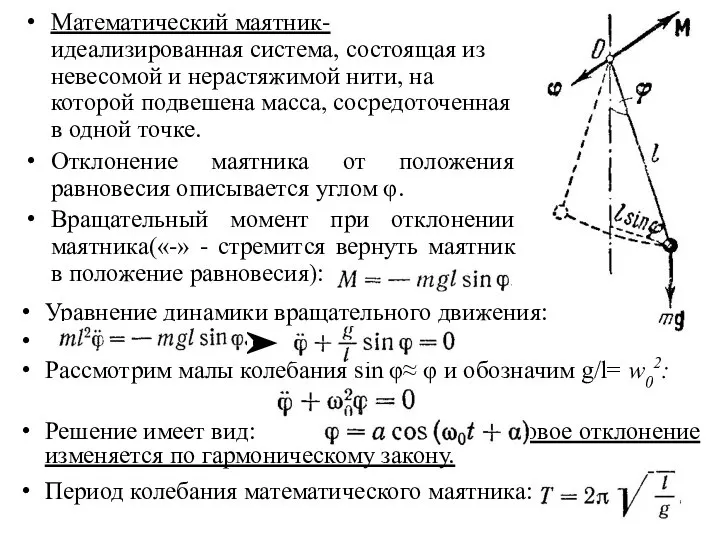
- 8. Математический маятник- идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в
- 9. Физическим маятником называется твёрдое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром
- 10. Период колебания физического маятника: Приведённая длина – это длина такого математического маятника, период колебаний которого совпадает
- 11. Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой. Пусть колебания
- 12. По правилу сложения векторов, суммарная амплитуда: Результирующая амплитуда: Начальная фаза: Таким образом, тело, участвуя в двух
- 13. При сложении двух гармонических колебаний одинакового направления и одинаковой частоты результирующее движение можно рассматривать как гармонические
- 14. - это есть периодическая функция с частотой ∆w. Частота пульсаций амплитуды называют частотой биения, равной разности
- 15. Два колебания с частотой w совершаются в направлении осей x и y. Начальная фаза первого колебания
- 16. 1) α = 0 Уравнение: 2) α = ± π Уравнение: Результирующее движение – гармонические колебания
- 17. 3) α = ± π/2 - Уравнение: α = π/2 Уравнение: Движение по часовой стрелке α
- 19. Скачать презентацию















 Краткая история развития радиосвязи
Краткая история развития радиосвязи Плоское движение тела
Плоское движение тела Шкала електромагнітних хвиль
Шкала електромагнітних хвиль Подобие физических явлений. Основы теории подобия. Примеры применения теории подобия для выбора условий испытаний моделей
Подобие физических явлений. Основы теории подобия. Примеры применения теории подобия для выбора условий испытаний моделей Откуда в наш дом приходит электричество?
Откуда в наш дом приходит электричество? Өлшеу қателігі. Құрал шкаласының және жүйелік қателерді есепке алу. Қос қателікті бағалау
Өлшеу қателігі. Құрал шкаласының және жүйелік қателерді есепке алу. Қос қателікті бағалау Тепловые двигатели и охрана окружающей среды
Тепловые двигатели и охрана окружающей среды Все о радиации
Все о радиации Аттестационная работа. Методическая разработка по выполнению исследовательской работы «От чего зависит сила Архимеда?»
Аттестационная работа. Методическая разработка по выполнению исследовательской работы «От чего зависит сила Архимеда?» Радиоизмерения и измерительные приборы
Радиоизмерения и измерительные приборы Электричество. Тест 13. Объяснение электризации тел
Электричество. Тест 13. Объяснение электризации тел Физические величины
Физические величины Механическая работа. Связь между работой и скоростью движения тела
Механическая работа. Связь между работой и скоростью движения тела Учиться и, когда придет время, прикладывать усвоенное к делу — разве это не прекрасно! Конфуций
Учиться и, когда придет время, прикладывать усвоенное к делу — разве это не прекрасно! Конфуций Электротехника. Электродвижущая сила источников электрической энергии и напряжение. Электромагнитня индукция
Электротехника. Электродвижущая сила источников электрической энергии и напряжение. Электромагнитня индукция Циклы углов и первый импульс как пророк. Циклы по цене и цели
Циклы углов и первый импульс как пророк. Циклы по цене и цели Основні засади метрологічного забезпечення вимірювань
Основні засади метрологічного забезпечення вимірювань Простейшая задача квантовой механики: частица в потенциальной яме (ящике). Квантовые точки
Простейшая задача квантовой механики: частица в потенциальной яме (ящике). Квантовые точки Момент силы. Правило момента
Момент силы. Правило момента Принцип работы кондиционера
Принцип работы кондиционера Ядерные технологии
Ядерные технологии Основы теории оболочек. Общие сведения о тонких пластинах
Основы теории оболочек. Общие сведения о тонких пластинах Поняття про топологію електричного кола та його граф
Поняття про топологію електричного кола та його граф Строительная физика
Строительная физика Презентация по физике "Нагревание тела" - скачать
Презентация по физике "Нагревание тела" - скачать  Понятие механической работы. Понятие мощности. Единицы измерения мощности
Понятие механической работы. Понятие мощности. Единицы измерения мощности Функції, властивості, класифікація та будова скелетних м’язових волокон. (Лекція 4)
Функції, властивості, класифікація та будова скелетних м’язових волокон. (Лекція 4) Система уравнений Максвелла. Основные уравнения электродинамики
Система уравнений Максвелла. Основные уравнения электродинамики