Содержание
- 2. Плоский изгиб Деформации и перемещения
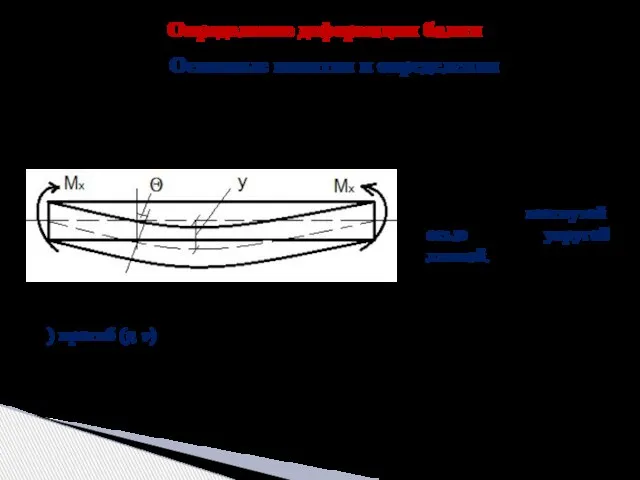
- 3. Определение деформации балки При изгибе балка прогибается, т.е. в плоскости действия сил (плоскость x0y) изменяется кривизна
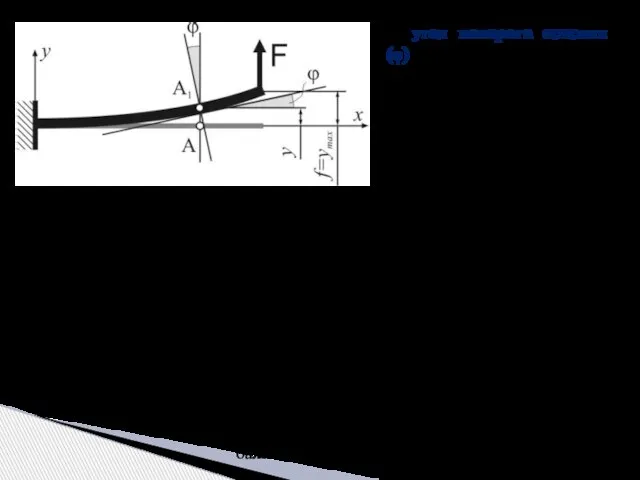
- 4. 2) угол поворота сечения (φ) – угол, на который сечение поворачивается относительно своего перво-начального положения (угол
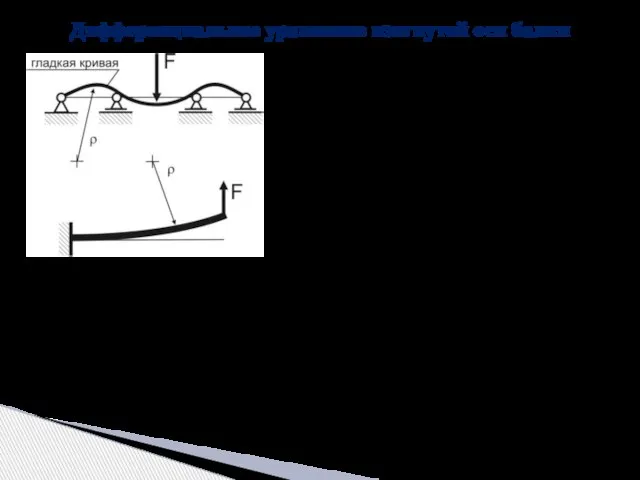
- 5. Дифференциальное уравнение изогнутой оси балки Исходя из физической природы явления изгиба, можем утверждать, что изогнутая ось
- 6. Приравняв правые части данных выражений, получим дифференциальное уравнение изогнутой оси балки, которое называется точным уравнением изогнутой
- 7. Решение дифференциального уравнения найдем, интегрируя обе его части по переменной x: Постоянные интегрирования C1, D1 находят
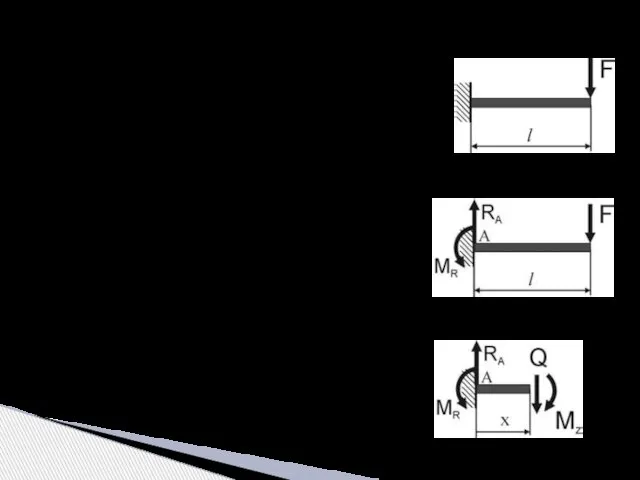
- 8. Рассмотрим решения данных уравнений на конкретном примере. Дано: Консольная балка длиной l, загруженная поперечной силой F.
- 9. в) определим угол поворота сечений балки Постоянную C1 найдем из условий закрепления, а именно – в
- 10. г) определим прогибы балки Постоянную D1 найдем из условий закрепления, а именно – в жесткой заделке
- 11. Использование изложенной техники определения перемещений для балок, имеющих несколько участков, оказывается достаточно трудоемким, так как для
- 12. Универсальное уравнение упругой линии. 2. Метод начальных параметров Правила метода: 1) начало координат необходимо выбирать общим
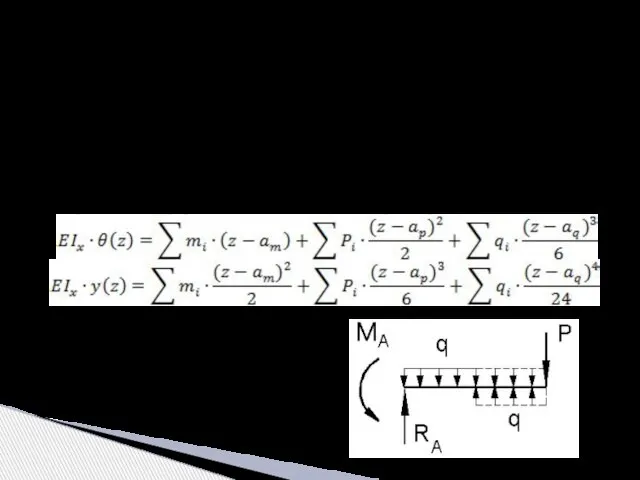
- 13. Рассмотрим некоторый отрезок балки, нагруженной произвольной системой сил и моментов (реакции опор также представляем как внешние
- 14. Универсальные уравнения для определения углов и прогибов балки при изгибе: Покажем, что C1 и D1 являются
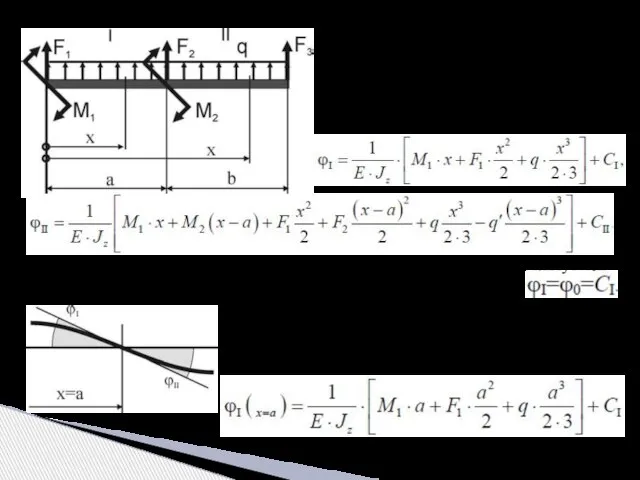
- 15. Рассмотрим два участка балки, загруженной произвольной нагрузкой. Составим для обоих участков универсальное уравнение углов: Для определения
- 16. тогда Проводя аналогичные рассуждения для уравнений, описывающих прогиб балки на двух соседних участках и на их
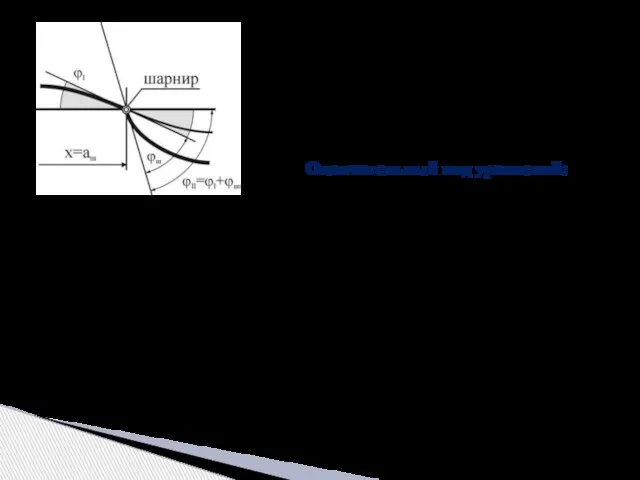
- 17. Величина φш – угол поворота в промежуточном (подвесном) шарнире, при этом aш – координата шарнира. При
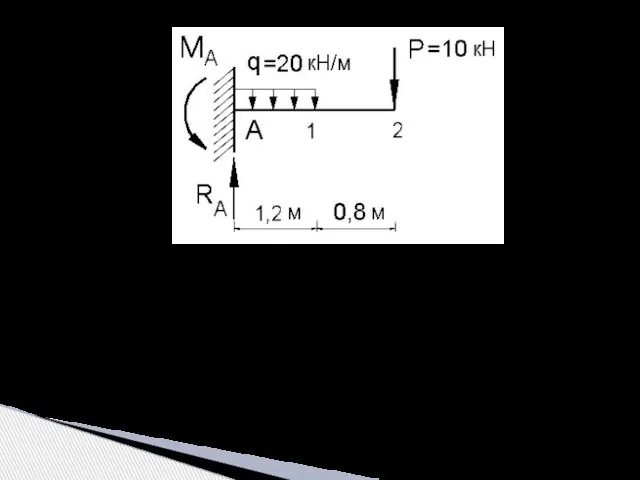
- 18. Для стальной консольной балки из двутаврового профиля № 30, определить углы поворота и прогибы сечений 1
- 19. Решение: Из условия равновесия балки определяем опорные реакции: Для определения перемещений балки в сечениях 1 и
- 21. Скачать презентацию




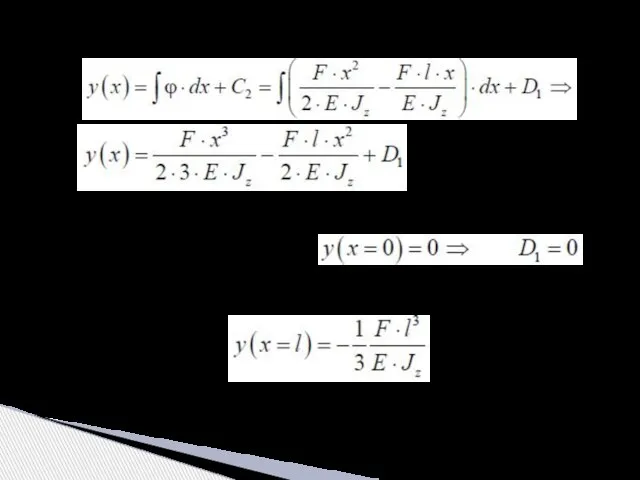





 Силы в природе
Силы в природе Испарение и конденсация. Насыщенные и ненасыщенные пары. Влажность воздуха
Испарение и конденсация. Насыщенные и ненасыщенные пары. Влажность воздуха 10 фактов об естествознании
10 фактов об естествознании Равновесие системы двух абсолютно твердых тел (сочленения)
Равновесие системы двух абсолютно твердых тел (сочленения) Управление образования администрации Чернушинского района Муниципальное Общеобразовательное Учреждение «Средняя общеобразова
Управление образования администрации Чернушинского района Муниципальное Общеобразовательное Учреждение «Средняя общеобразова АВ120
АВ120 Бета-распад. Характеристика бета-излучения. Взаимодействие бета-излучения с веществом. Гамма-излучения
Бета-распад. Характеристика бета-излучения. Взаимодействие бета-излучения с веществом. Гамма-излучения Поперечные и продольные волны
Поперечные и продольные волны Пространство и время в классической и квантовой физике
Пространство и время в классической и квантовой физике Эксплуатационная живучесть воздушных судов
Эксплуатационная живучесть воздушных судов Равновесное состояние кристаллической решетки. Фононы. (Лекция 5)
Равновесное состояние кристаллической решетки. Фононы. (Лекция 5) Введение в нанотехнологии
Введение в нанотехнологии Siltumfizikas pamati. Enerģijas mērvienības, spiediens, degšana, siltumapmaiņa, tvaika veidošanās
Siltumfizikas pamati. Enerģijas mērvienības, spiediens, degšana, siltumapmaiņa, tvaika veidošanās Сұйықтықтарды тасымалдау
Сұйықтықтарды тасымалдау Устройство колёсных пар с буксовыми узлами грузовых вагонов
Устройство колёсных пар с буксовыми узлами грузовых вагонов Метапредметный подход на уроках физики
Метапредметный подход на уроках физики Математическое моделирование подавления волны горения при различных внешних воздействиях
Математическое моделирование подавления волны горения при различных внешних воздействиях Основы молекулярной физики и термодинамики
Основы молекулярной физики и термодинамики Рентгеновское излучение
Рентгеновское излучение Волновая оптика
Волновая оптика Плоская система сходящихся сил
Плоская система сходящихся сил Электромагнитные волны
Электромагнитные волны Типы ядерных реакторов
Типы ядерных реакторов Свободное падение тел
Свободное падение тел МСОШ№1 Кананыхина Л.П.
МСОШ№1 Кананыхина Л.П. Солнце Урок для 11 класса Учитель Тарасенко Е.А.
Солнце Урок для 11 класса Учитель Тарасенко Е.А. Закон сохранения импульса
Закон сохранения импульса Электрооборудование автомобилей. Введение. (Урок 1)
Электрооборудование автомобилей. Введение. (Урок 1)