Содержание
- 2. ТЕОРИЯ ПОЛОГИХ ОБОЛОЧЕК Пологой будем называть оболочку, на поверхности которой можно ввести некоторую систему криволинейных коор-динат,
- 3. В результате уравнения общей теории оболочек упрощаются следующим образом Уравнения равновесия принимают вид Соотношения упругости сохраняются
- 4. Соответственно упрощаются и выражения для перерезывающих сил. Из двух последних уравнений равновесия имеем С учетом приведенных
- 5. РАСЧЕТ ПОЛОГИХ ОБОЛОЧЕК Ввиду того, что построенная система уравнений является приближенной, при расчете пологих оболочек, как
- 6. Если на оболочку не действуют касательные поверхностные нагрузки, т. е. qx=qy=0, система уравнений пологих оболочек может
- 7. Таким образом, теория пологих оболочек сводится к двум уравнениям относительно прогиба w и функции напряжений φ.
- 8. Для шарнирно опертой по краям прямоуголь-ной в плане пологой оболочки (см. рис) решение может быть построено
- 9. Определяя из системы wmn для оболочки, показанной на рисунке, окончательно получим
- 10. Решение может быть получено и в результате подстановки разложений для w и р в уравнение восьмого
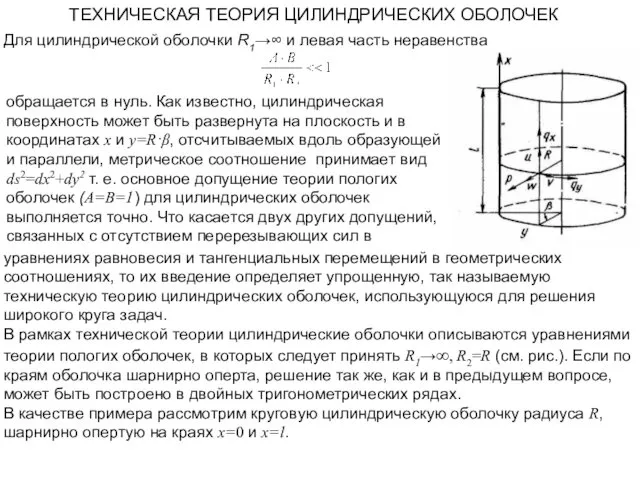
- 11. ТЕХНИЧЕСКАЯ ТЕОРИЯ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Для цилиндрической оболочки R1→∞ и левая часть неравенства обращается в нуль. Как
- 12. Граничные условия на этих краях имеют вид: Пусть на оболочку действует нормальное давление р(х,β), распределенное симметрично
- 13. Решая эти уравнения, можно найти umn, vmn, wmn в зависимости от коэффициентов разложения нагрузки ртn. Аналогичным
- 14. ПОЛУБЕЗМОМЕНТНАЯ ТЕОРИЯ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Цилиндрическая оболочка является распространенным элементом конструкций самого разнообразного назначения и методы расчета
- 15. Для других граничных условий решение данного уравнения в силу его периодичности по окружной координате у может
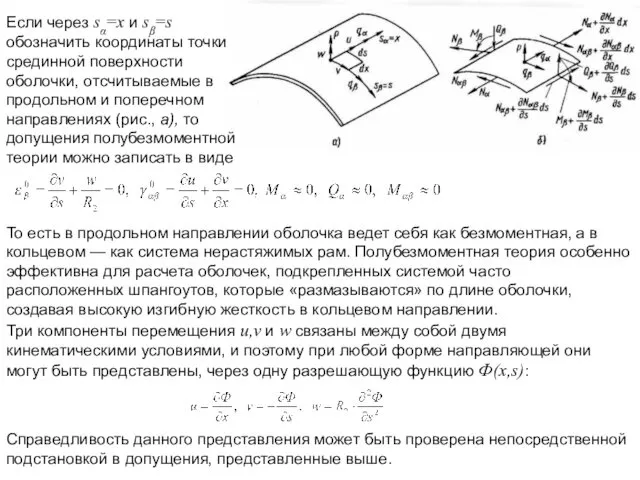
- 16. Если через sα=х и sβ=s обозначить координаты точки срединной поверхности оболочки, отсчитываемые в продольном и поперечном
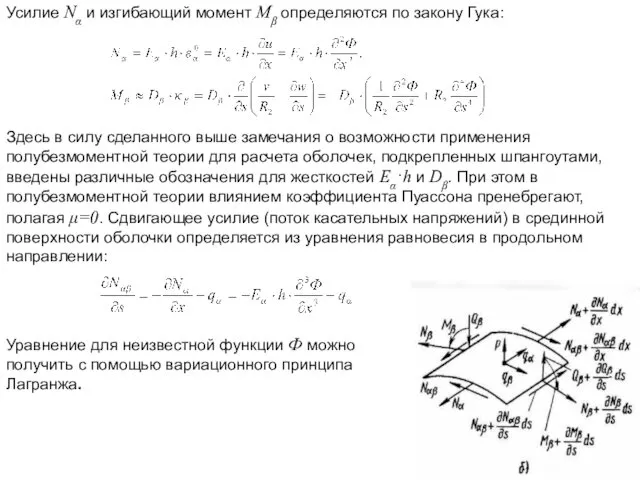
- 17. Усилие Nα и изгибающий момент Мβ определяются по закону Гука: Здесь в силу сделанного выше замечания
- 18. Потенциальная энергия деформации полубезмоментной оболочки с учетом введенных допущений будет иметь вид Вариация работы поверхностных нагрузок
- 19. Круговая цилиндрическая оболочка Рассмотрим прямую замкнутую круговую цилиндрическую оболочку, для которой R2=R=const и х=R·α, s=R·β (см.
- 20. Чтобы этот интеграл обращался в нуль, на каждом торце должны быть заданы перемещения (тогда δи=0, δν=0)
- 21. В силу ортогональности тригонометрических функций решение распадается на отдельные составляющие. При этом в случае n=0, представляющем
- 23. Скачать презентацию

















 Қанның реологиялық қасиеттері. (Дәріс 12)
Қанның реологиялық қасиеттері. (Дәріс 12) Свойства жидкостей (лекция 10)
Свойства жидкостей (лекция 10) Оптические явления в природе
Оптические явления в природе Лекция 15. Основы физики прочности и пластичности
Лекция 15. Основы физики прочности и пластичности  Атмосферное давление
Атмосферное давление Тепловой и гидравлический расчёт ядерного реактора
Тепловой и гидравлический расчёт ядерного реактора Понятие излучения. Поток излучения. Реактор как источник излучений. Первичные и вторичные источники излучений
Понятие излучения. Поток излучения. Реактор как источник излучений. Первичные и вторичные источники излучений Шкалы разные нужны, шкалы всякие важны Какие существуют шкалы для измерения температуры?
Шкалы разные нужны, шкалы всякие важны Какие существуют шкалы для измерения температуры? Презентация по физике "Агрегатные состояния вещества" - скачать
Презентация по физике "Агрегатные состояния вещества" - скачать  Курс общей физики
Курс общей физики Основи МКТ Газові закони
Основи МКТ Газові закони  Академия Транспортных Технологий
Академия Транспортных Технологий Экспериментальная проверка закона Джоуля-Ленца
Экспериментальная проверка закона Джоуля-Ленца Силовые линии электрического поля. Напряженность заряженного шара
Силовые линии электрического поля. Напряженность заряженного шара Попов Александр Степанович
Попов Александр Степанович ПОДГОТОВКА К ЕГЭ: РЕШЕНИЕ ЗАДАЧ НА ФОТОЭФФЕКТ Волковская Любовь Александровна учитель физики МБОУСОШ № 27 ст. Старотитаров
ПОДГОТОВКА К ЕГЭ: РЕШЕНИЕ ЗАДАЧ НА ФОТОЭФФЕКТ Волковская Любовь Александровна учитель физики МБОУСОШ № 27 ст. Старотитаров Ultraskaņa, infraskaņa un vibrācijas
Ultraskaņa, infraskaņa un vibrācijas Статика
Статика Вынужленные колебания, затухающие колебания
Вынужленные колебания, затухающие колебания Оптика. Оптическая сила линзы. Формула тонкой линзы. Линейное увеличение
Оптика. Оптическая сила линзы. Формула тонкой линзы. Линейное увеличение Повторение: основные понятия и уравнения кинематики
Повторение: основные понятия и уравнения кинематики Электромагнитное поле Презентация по физике
Электромагнитное поле Презентация по физике Растровый выбор. Муар
Растровый выбор. Муар Леткинская средняя школа Старошайговского района Подготовила: учитель физики Недякина Екатерина Ивановна
Леткинская средняя школа Старошайговского района Подготовила: учитель физики Недякина Екатерина Ивановна Телескоп
Телескоп Альтернативный шнекоход
Альтернативный шнекоход Общие положения по организации связи в сухопутных войсках. Система связи. (Тема 1.2)
Общие положения по организации связи в сухопутных войсках. Система связи. (Тема 1.2) Закон сохранения импульса
Закон сохранения импульса