Содержание
- 2. Уравнение Шредингера для водородоподобного ато-ма имеет вид: (14.1) где оператор Лапласа: (14.2) Решение этого уравнения впервые
- 3. Запишем оператор Лапласа в виде (14.3) где - оператор Лежандра (13.20). Решение урав-нения Шредингера ищем в
- 4. Левая часть уравнения (14.6) зависит только от r, правая часть только от θ, φ, поэтому для
- 5. Уравнение (14.8) более универсально: оно одинако-во для всех сферически - симметричных полей, по-этому займемся сначала этим
- 6. Левая часть уравнения (14.11) зависит только от θ, правая часть только от φ, поэтому для того,
- 7. Очевидно, что решение (14.14) удовлетворяет усло-вию ограниченности. Но т.к. φ - циклическая пере-менная, а область ее
- 8. Теперь рассмотрим уравнение (14.13). Введем вмес-то θ новую переменную ξ: ξ = cosθ, -1 ≤ ξ
- 9. Функции P(ξ) называются "присоединенными полино-мами Лежандра", их общий вид был найден еще в 18-м веке французским
- 10. Определив константу λ = l(l+1), подставим ее в урав-нение (14.7) (14.20) Решение этого уравнения также давно
- 11. Наиболее простые из полиномов Лагерра имеют вид: (14.21) Итак, волновые ψ-функции (собственные функции уравнения (14.1)) содержат
- 12. Подведем итоги. Энергия электрона определяется формулой, в точности совпадающей с результа-том, полученным в рамках теории Бора:
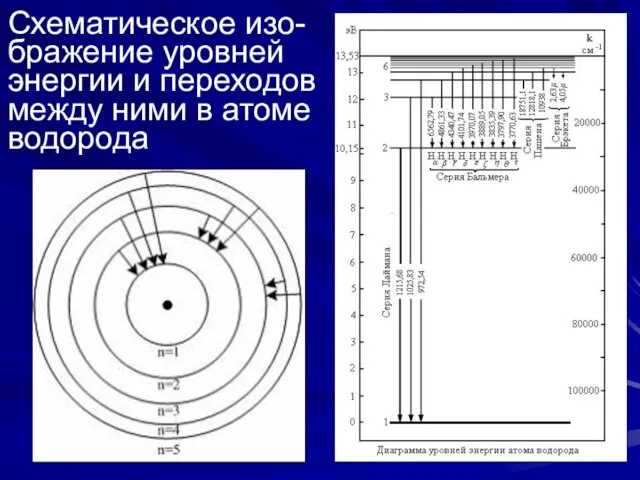
- 13. Схематическое изо- бражение уровней энергии и переходов между ними в атоме водорода
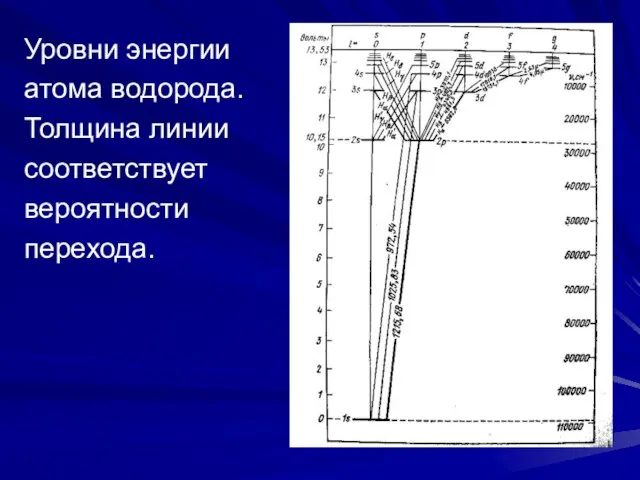
- 14. Уровни энергии атома водорода. Толщина линии соответствует вероятности перехода.
- 15. Момент импульса электрона в атоме определяет- ся орбитальным квантовым числом l: (14.24) где орбитальное квантовое число
- 16. Проекция момента импульса на выделенное на-правление (например, на направление внешне-го магнитного поля) определяется магнитным квантовым числом
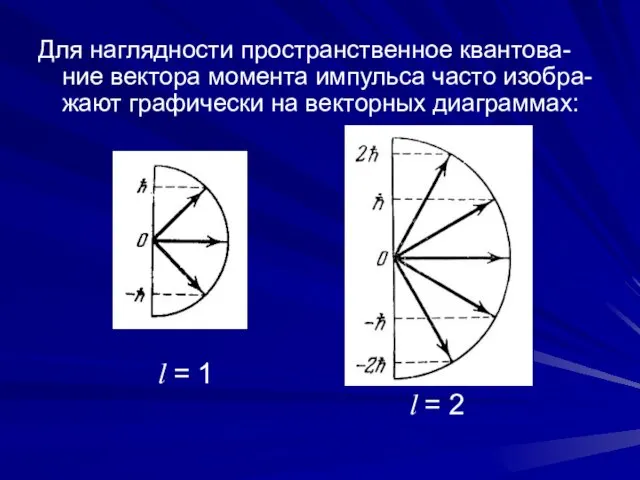
- 17. Для наглядности пространственное квантова-ние вектора момента импульса часто изобра-жают графически на векторных диаграммах: l = 1
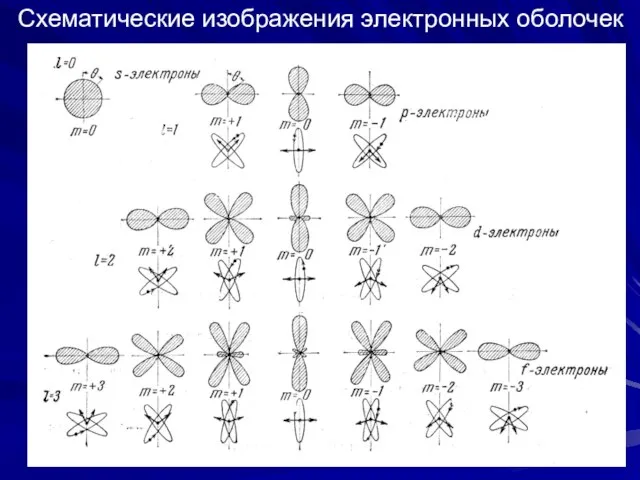
- 18. Графические изображения электронных s-, p- и d-оболочек
- 19. Графическое изображение 4f-оболочки
- 20. Схематические изображения электронных оболочек
- 22. Скачать презентацию















 Гидродинамика. Полная диаграмма циркуляции воды в трубе
Гидродинамика. Полная диаграмма циркуляции воды в трубе ВКР: Технологический процесс изготовления гребного винта
ВКР: Технологический процесс изготовления гребного винта Законы Ньютона
Законы Ньютона Презентация по физике "Виды движения" - скачать
Презентация по физике "Виды движения" - скачать  Презентация по физике "Способы теплопередачи" - скачать
Презентация по физике "Способы теплопередачи" - скачать  Термодинамика
Термодинамика Лекция №21. Опыты холостого хода и короткого замыкания. Потери и КПД трансформатора. Регулирование напряжения трансформатора
Лекция №21. Опыты холостого хода и короткого замыкания. Потери и КПД трансформатора. Регулирование напряжения трансформатора Нанотехнологии. Лекция 7. Классификация способов получения наноматериалов
Нанотехнологии. Лекция 7. Классификация способов получения наноматериалов Fluorescence lyman-alpha stratospheric hygrometer (flash): application on meteorological balloons, long duration balloons
Fluorescence lyman-alpha stratospheric hygrometer (flash): application on meteorological balloons, long duration balloons Нове застосування лінз Нове застосування лінз
Нове застосування лінз Нове застосування лінз  Презентация по физике "Шкала Фаренгейта предложена в 1709г" - скачать
Презентация по физике "Шкала Фаренгейта предложена в 1709г" - скачать  Сила Ампера і сила Лоренца
Сила Ампера і сила Лоренца Агрегатное состояние вещества
Агрегатное состояние вещества Архитектурная акустика Лекция №2
Архитектурная акустика Лекция №2  Краткая история развития радиосвязи
Краткая история развития радиосвязи Классификация магнитных материалов и их применение в микро- и наноэлектронике. (Лекция 13)
Классификация магнитных материалов и их применение в микро- и наноэлектронике. (Лекция 13) Лабораторные работы по физике. 7 класс
Лабораторные работы по физике. 7 класс Импульс. Закон сохранения импульса. Энергия. Закон сохранения механической энергии
Импульс. Закон сохранения импульса. Энергия. Закон сохранения механической энергии ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ
ТЕПЛОМАССОПЕРЕНОС В ЯДЕРНО-ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ  Напівпровідникові прилади та їх застосування
Напівпровідникові прилади та їх застосування Теория автоматического управления
Теория автоматического управления Надпровідність
Надпровідність Брейн-ринг «Юные знатоки физики»
Брейн-ринг «Юные знатоки физики» Прямой метод решения уравнений в матричной форме. Организация итерационного процесса. Проблема сходимости численных схем
Прямой метод решения уравнений в матричной форме. Организация итерационного процесса. Проблема сходимости численных схем Презентация по физике "Действие магнитного поля" - скачать
Презентация по физике "Действие магнитного поля" - скачать  Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Проводники и диэлектрики
Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Проводники и диэлектрики Факторы возникновения световой волны. Фотометрические величины и единицы их измерения
Факторы возникновения световой волны. Фотометрические величины и единицы их измерения Вибрации и колебания
Вибрации и колебания