Содержание
- 2. 200 ВОПРОСЫ 11. Принцип относительности в механике. Инерциальные системы отсчёта. Преобразования Галилея. 12. Неинерциальные системы отсчёта.
- 3. 200 Вопрос № 11. Принцип относительности в механике. Преобразования Галилея. Инерциальные системы отсчёта.
- 4. 200 Инерциальные системы Рассмотрим две системы отсчёта, одна покоится (K), другая (K/) движется относительно другой со
- 5. 200
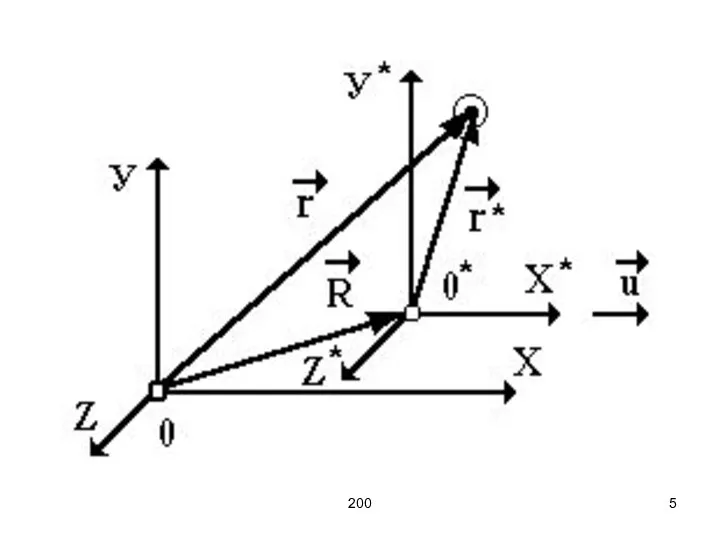
- 6. 200 Запишем связь между координатами (x, y, z) и (x/, y/, z/) точки «P» в системах
- 7. 200 Получаем четыре уравнения это преобразование Галилея, используем его если V0
- 8. 200 Дифференцируем по времени:
- 9. 200 Или в следующем виде (напоминаем, что только для выбранной схемы, рисунка)
- 10. 200 Перейдём к векторам Дифференцируем или для уравнения движения
- 11. 200 Уравнения динамики не изменяются при переходе от одной инерциальной системы отсчёта к другой, то есть
- 12. 200 Итак, все инерциальные системы отсчёта инвариантны: Уравнения движения выглядят одинаково (дифференциальные уравнения), но движения разные,
- 13. 200
- 14. 200 12. Неинерциальные системы отсчёта. Сила инерции.
- 15. 200 Неинерциальные системы Рассмотрим две системы отсчёта, одна инерциальная, вторая – неинерциальная, Имеется некоторое тело, которое
- 16. 200 Разность ускорений тела в инерциальной и неинерциальной системах отсчёта (для поступательного движения) a – одинаково
- 17. 200 Через 2-й закон Ньютона представим ускорения. Инерциальная система: Неинерциальная система: m – масса тела.
- 18. 200 Отсюда, при F = 0 тело будет двигаться, в неинерциальной системе отсчёта с ускорением –a,
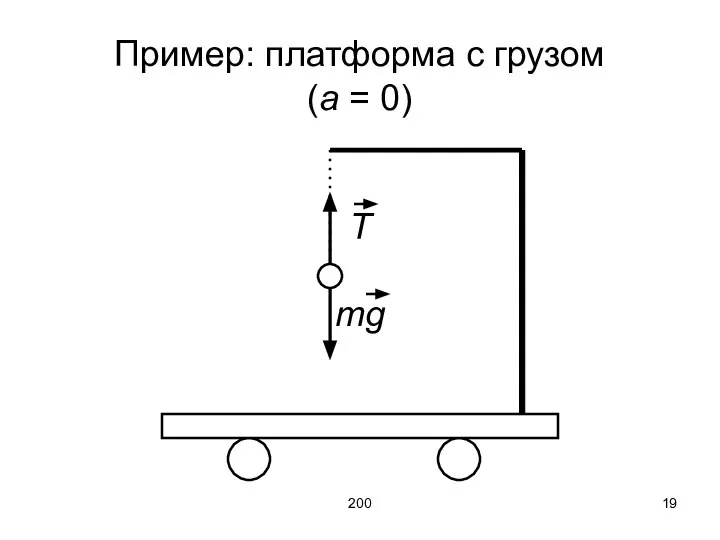
- 19. 200 Пример: платформа с грузом (a = 0) T mg
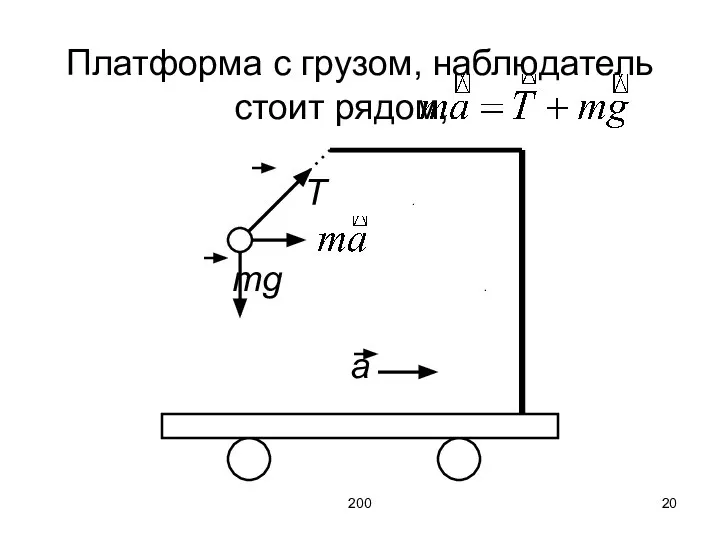
- 20. 200 Платформа с грузом, наблюдатель стоит рядом, T . mg . a
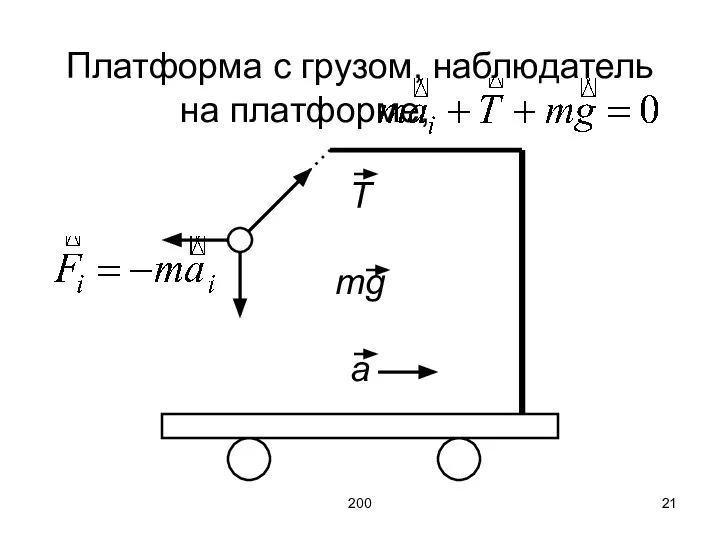
- 21. 200 Платформа с грузом, наблюдатель на платформе, T mg a
- 22. 200 Все силы в физике обусловлены взаимодействием тел, то есть одно тело действует на другое, и
- 23. 200
- 24. 200 13. Силы инерции во вращающихся неинерциальных системах и системах. Принцип эквивалентности масс.
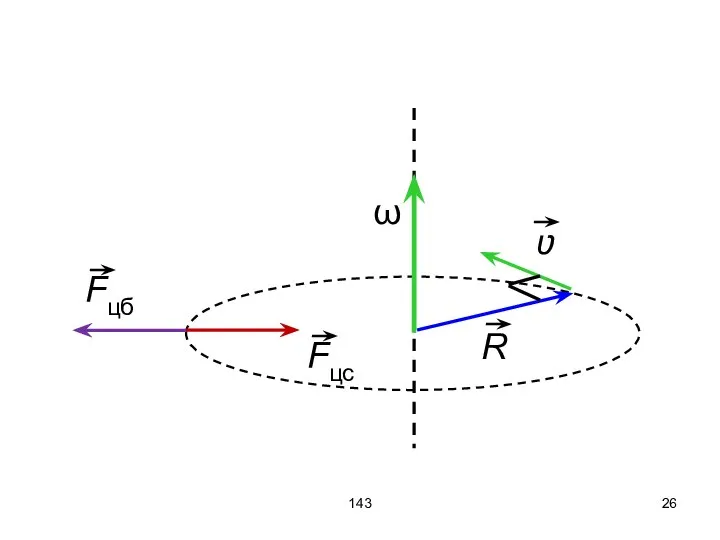
- 25. 200 Рассмотрим движение тела по окружности. В инерциальной системе тело удерживается на окружности центростремительной силой. В
- 26. 143
- 27. 200 Если наблюдать из инерционной системы отсчёта (наблюдатель находится рядом, не двигается), то необходимо использовать силу
- 28. 200 Если наблюдать из неинерционной системы отсчёта (наблюдатель двигается по окружности радиусом R с угловой скоростью
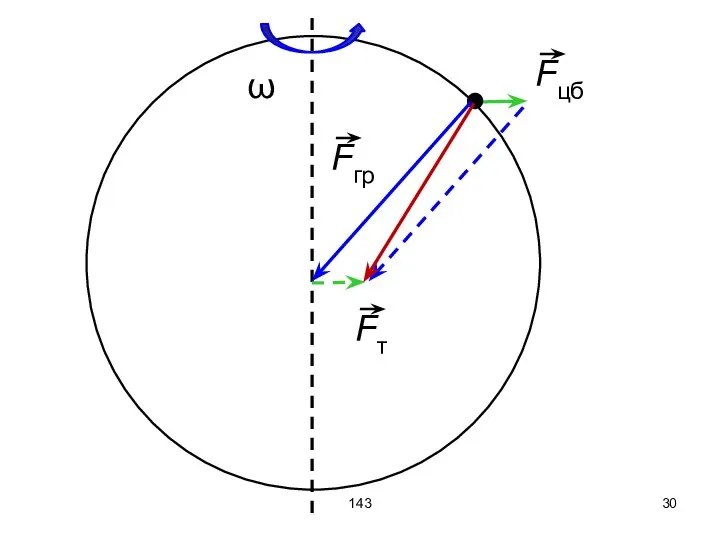
- 29. 200 Влияние центробежной силы на силу тяжести. Сила гравитационного взаимодействия притягивает тела на поверхности Земли к
- 30. 143
- 31. 200 Центробежная сила на экваторе за счёт вращения Земли вокруг своей оси: aцб = 3,4 см/с2.
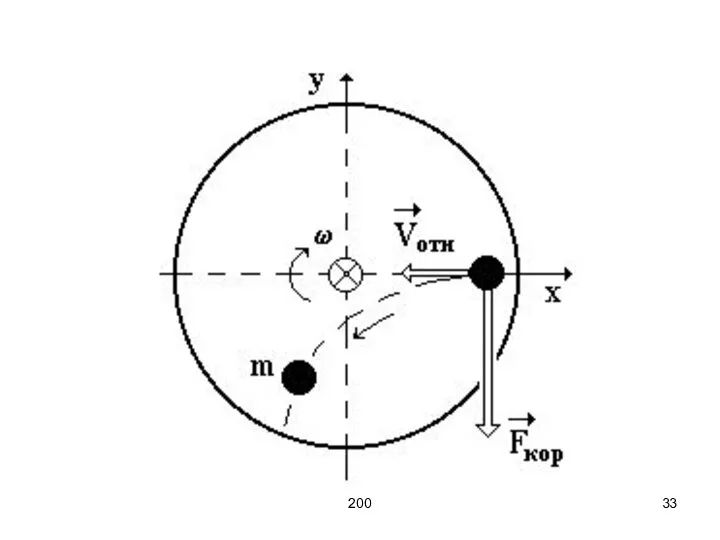
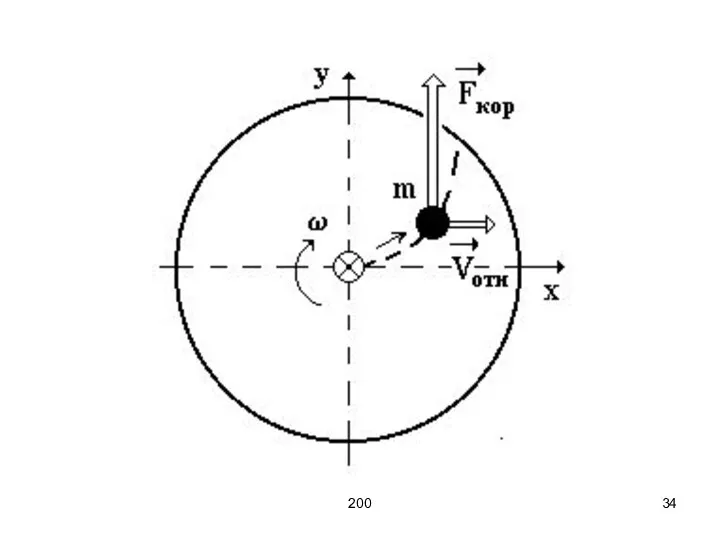
- 32. 200 При движении тела относительно вращающейся системы отсчёта, кроме центробежной силы инерции, появляется ещё одна сила,
- 33. 200
- 34. 200
- 35. 200 Если ʋотн II ω и ʋотн ן R: Fк = 0. При движении параллельно оси
- 36. 200 Принцип эквивалентности масс. Все физические явления в гравитационном поле происходят совершенно так же, как и
- 37. 200 (Или) масса гравитационная равняется массе инерционной
- 38. 200 Пустили фотон с некоторой частотой ν сверху вниз. Энергия и масса фотона: Eф = mc2,
- 39. 200 Изменение частоты: что и было зафиксировано. Точность измерений была:
- 40. 200
- 41. 200 ЛЕКЦИЯ № 5 Элементы релятивистской механики
- 42. 200 ВОПРОСЫ 14. Предпосылки появления специальной теории относительности (СТО). 15. Преобразования Лоренца. Следствия из преобразований Лоренца.
- 43. 200 14. Предпосылки появления специальной теории относительности (СТО).
- 44. 200 Классическая физика рассматривает движение макротел с медленными скоростями. Описание взаимодействия тел с помощью потенциальной энергии
- 45. 200 Однако это противоречит экспериментальным данным, которые появились к концу XIX века. По Эйнштейну существует максимальная
- 46. 200 В связи с механическим принципом относительности Галилея возникает вопрос: равноправны ли все инерциальные системы отсчета
- 47. 200 Как показал, Эйнштейн принцип относительности распространяется на любые физические явления, а не только механические.
- 48. 200 Позднее им была создана специальная теория относительности (СТО) для движения тел и частиц со скоростями
- 49. 200 Позднее Эйнштейн создал общую теорию относительности (1916г.), которая учитывает большие гравитационные поля. Но рассмотрим только
- 50. 200 1-й постулат (релятивистский принцип относительности): в любых инерциальных системах отсчета все физические явления при одних
- 51. 200 Следовательно, все физические законы инвариантны (независимы) по отношению к выбору инерциальной системы отсчета.
- 52. 200 2-й постулат (принцип инвариантности скорости света в вакууме): Скорость света в вакууме не зависит от
- 53. 200 Эти принципы приводят к тому, что события одновременные в классической механике в релятивистской становятся относительными.
- 54. 200
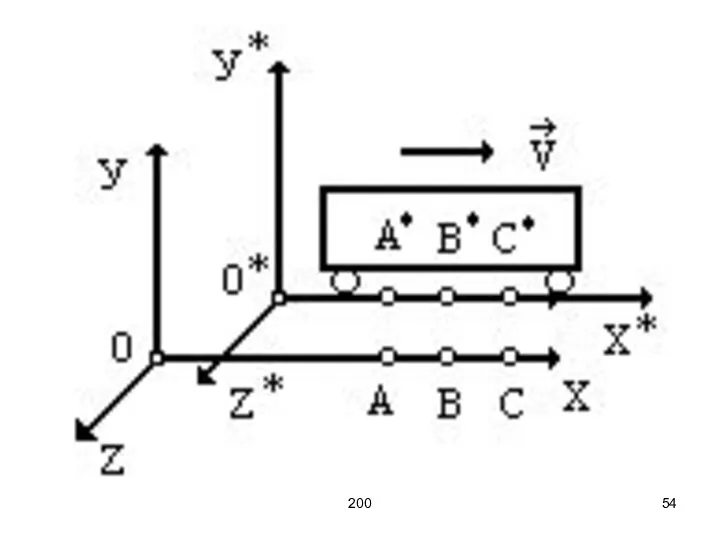
- 55. 200 Для вагона точки обозначим через А*, С* и В*, причем А*В*= В*С*. В тот момент,
- 56. 200 Наблюдатель же в точке В*, движущийся в направлении точки С*, заметит вначале вспышку, произведенную в
- 57. 200 Наблюдатель на Земле, находясь в точке В увидит два пространственно разделенных события, произошедшие одновременно, тогда
- 58. 200 Следовательно, понятие одновременности относительно, т. е. два пространственно разделенных события, одновременные в одной ИСО не
- 59. 200 Это относится лишь к событиям, между которыми отсутствуют причинно-следственная связь. Причинно связанные события ни в
- 60. 200
- 61. 200 15. Преобразования Лоренца. Следствия из преобразований Лоренца: сокращение длины движущихся тел и замедление темпа хода
- 62. 200 Для описания движения в СТО используют преобразования Лоренца, позволяющие переходить от координат одной инерциальной системы
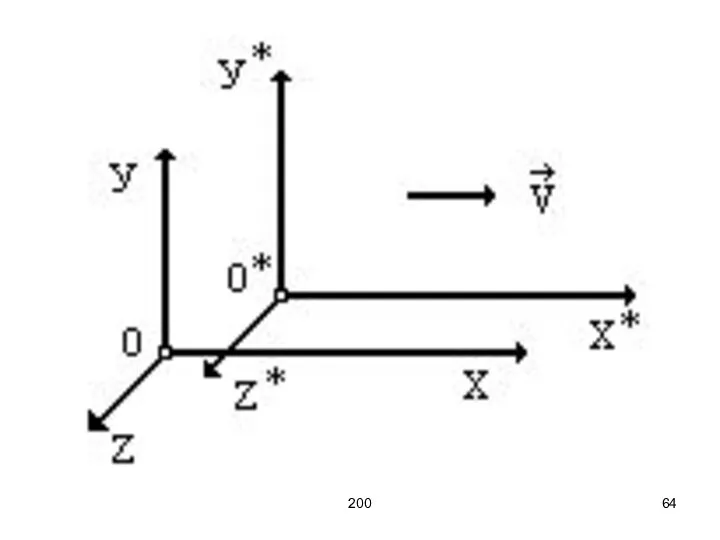
- 63. 200 Преобразования Лоренца имеют наиболее простой вид в случае, когда сходственные оси декартовых координат неподвижной К
- 64. 200
- 65. 200 Начало отсчета времени выбирается в тот момент, когда координаты начала 0 и 0' обеих инерциальных
- 66. 200 y = y′; y′ = y; z = z′; z′ = z;
- 67. 200 Следствия преобразований Лоренца. Одновременность событий в разных системах отсчёта. В системе К в точках x1
- 68. 200 Но в системе К′ эти события произойдут моменты времени: Но если события причинно связанные, ни
- 69. 200 Промежуток времени между событиями. Существуют события, вызванные причинно-следственной связью. Например, чтобы камень упал в воду,
- 70. 200 Бросок является причиной, а падение камня в воду – следствием. 1) сначала происходит событие, являющееся
- 71. 200 В связи с этим в СТО, хотя время и преобразуется, но последовательность во времени между
- 72. 200 Тогда скорость пули Используя преобразования Лоренца найдем промежуток времени между этими же событиями в ИСО
- 73. 200 где скорости u и ʋ t1, то и t′2 > t′1.
- 74. 200 Поэтому если событие происходит в одной и той же точке, т. е. х1 = х2.
- 75. 200 т. е. промежуток времени между двумя событиями имеет меньшее значение в ИСО, связанной с точкой,
- 76. 200 Промежуток времени Δt – собственное время тела, в системе, где тело покоится. Собственное время всегда
- 77. 200 Эксперименты подтвердили полученный результат. Например, время жизни покоящихся мюонов τ ≈ 2 мкс. Мюоны же
- 78. 200 Длина тел в разных системах. Длина стержня в ИСО равна разности координат его концов. Например,
- 79. 200 Однако результат изменяется, когда наблюдатель и стержень движутся относительно друг друга. Понятие одновременности относительно и
- 80. 200 Для вычисления длины стержня используют преобразования Лоренца. Например, пусть некоторый стержень расположен параллельно оси Х
- 81. 200 В ИСО К′, движущейся относительно ИСО К равномерно и прямолинейно со скоростью ʋ = const
- 82. 200 Используя преобразования Лоренца, имеем то есть
- 83. 200 Если координаты концов отрезка в ИСО К′ измерены одновременно (так как t′2 = t′1.), то
- 84. 200 Следовательно, длина отрезка в любой ИСО, относительно которой он движется, меньше длины отрезка в неподвижной
- 85. 200
- 86. 200 16. Закон сложения скоростей в СТО. Релятивистский импульс. Энергия релятивистской частицы. Инварианты преобразования Лоренца. Интервал.
- 87. 200 Интервал Любые события характеризуются точкой, где оно произошло, имеющей координаты х, у, z и временем
- 88. 200 В обычной механике рассматривают пространственные координаты отдельно от времени и расстояние между двумя точками является
- 89. 200 В релятивистской механике эта величина не является инвариантной. Приходится учитывать четвёртую величину – время. В
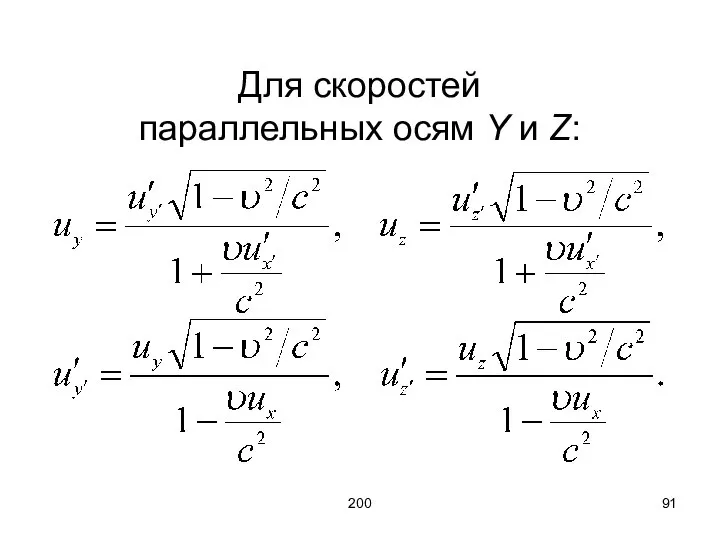
- 90. 200 Релятивистский закон сложения скоростей: где ux – скорость м. т. (тела) в ИСО К; u′x′
- 91. 200 Для скоростей параллельных осям Y и Z:
- 92. 200 Релятивистский импульс в виде обеспечивает инвариантность закона сохранения импульса по отношению к преобразованиям Лоренца,
- 93. 200 здесь dr – перемещение частицы (материальной точки) в той ИСО, в которой определяется её импульс;
- 94. 200 Так как, то где
- 95. 200 Следовательно, релятивистский импульс частицы
- 96. 200 Уравнение динамики
- 97. 200 Энергия Энергия покоя E0 = m0c2, Энергия релятивистской частицы m0 – масса покоя.
- 98. 200 Кинетическая энергия релятивистской частицы
- 99. 200 Полная энергия
- 100. 200 Инварианта энергии и импульса Величина E/c, px, py, pz образует четырёхвектор (вектор энергии-импульса).
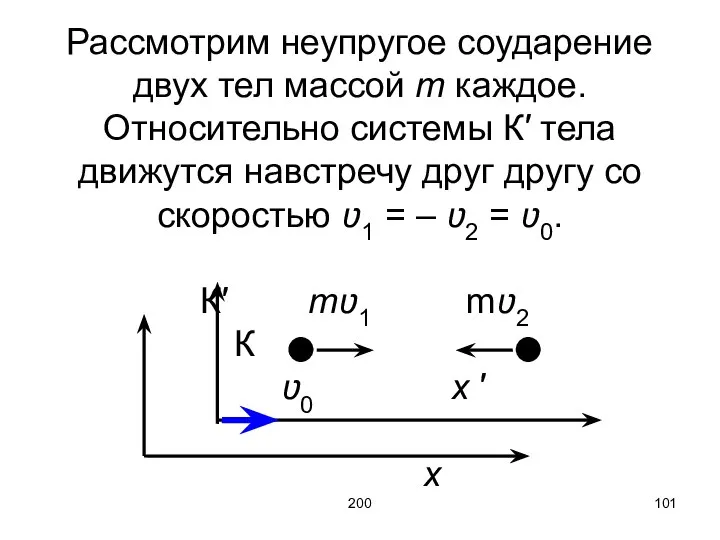
- 101. 200 Рассмотрим неупругое соударение двух тел массой m каждое. Относительно системы К′ тела движутся навстречу друг
- 102. 200 Система К′ движется относительно системы К со скоростью ʋ0. В системе К′ В системе К
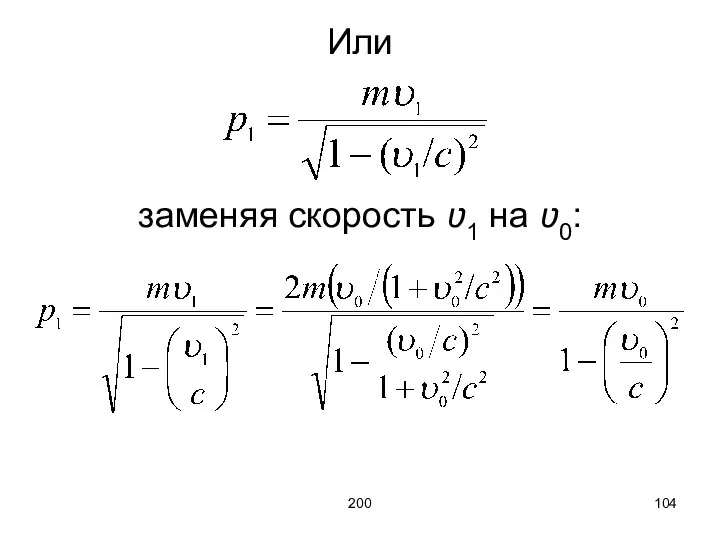
- 103. 200 Согласно переходу импульс до удара будет
- 104. 200 Или заменяя скорость ʋ1 на ʋ0:
- 105. 200 Но должно быть
- 106. 200 Такой результат получили, так как не учли массу системы
- 107. 200 Это обусловлено тем, что кинетическая энергия частиц превратилась в эквивалентное количество энергии покоя, а это
- 108. 200
- 109. 200 ЛЕКЦИЯ № 6 Элементы механики твёрдого тела.
- 110. 200 ВОПРОСЫ 17. Условия равновесия твёрдого тела. Мгновенная ось вращения. 18. Кинетическая энергия вращающегося твёрдого тела.
- 111. 200 19. Основной закон динамики вращательного движения твёрдого тела. Момент инерции, его свойства. Теорема Штейнера (теорема
- 112. 200 17. Условия равновесия твёрдого тела. Мгновенная ось вращения.
- 113. 200 В случае описания положения и/или движения материальной точки достаточно 3-х степеней свободы. Степень свободы –
- 114. 200 Для абсолютно твёрдого тела (тело, деформациями которого можно пренебречь) необходимо 6 степеней свободы: 3 –
- 115. 200 Уравнение динамики движения центра масс Уравнение динамики вращательного движения
- 116. 200 Если Fвнеш и Mвнеш равны нулю, то тело будет находиться в равновесии. Условия равновесия твёрдого
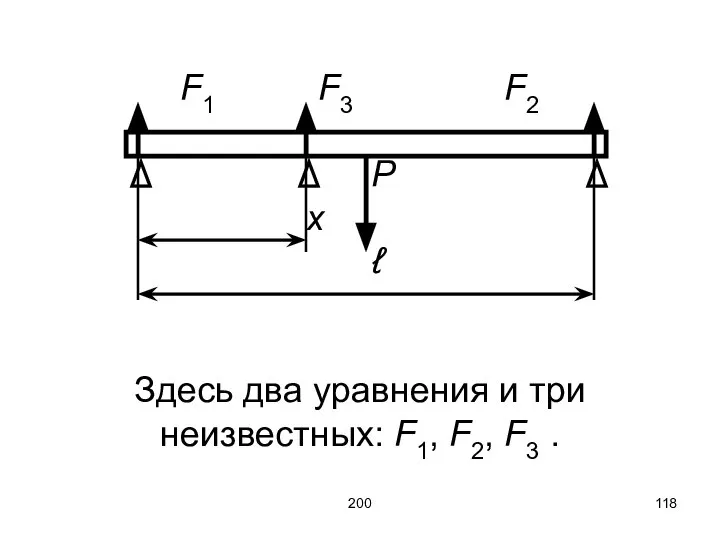
- 117. 200 Не всегда можно пользоваться моделью абсолютно твёрдого тела. Пример: рассмотрим балку на 3-х опорах. Для
- 118. 200 F1 F3 F2 P x ℓ Здесь два уравнения и три неизвестных: F1, F2, F3
- 119. 200 Данная задача оказалась неопределённой, решить её можно, если придать одной из сил произвольное значение. Механические
- 120. 200 Физики про себя шутят: если им дать задачу о равновесии стола на 4 ножках, то
- 121. 200 Любое движение твёрдого тела может быть представлено как наложение двух типов движения: поступательного и вращательного;
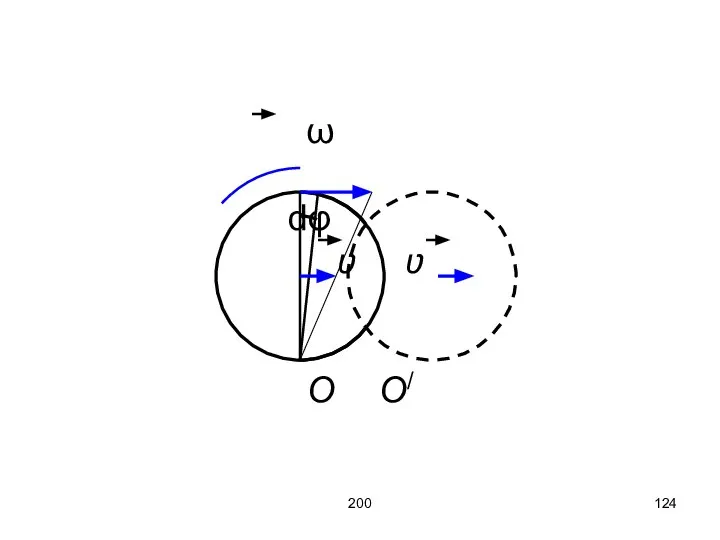
- 122. 200 Элементарное перемещение твёрдого тела при плоском движении всегда можно представить как поворот вокруг некоторой оси,
- 123. 200 Пример: катящийся цилиндр. Плоское движение твёрдого тела можно рассматривать как ряд последовательных элементарных вращений вокруг
- 124. 200 ω dφ ʋ ʋ O O/
- 125. 200
- 126. 200 18. Кинетическая энергия вращающегося твёрдого тела. Работа момента силы.
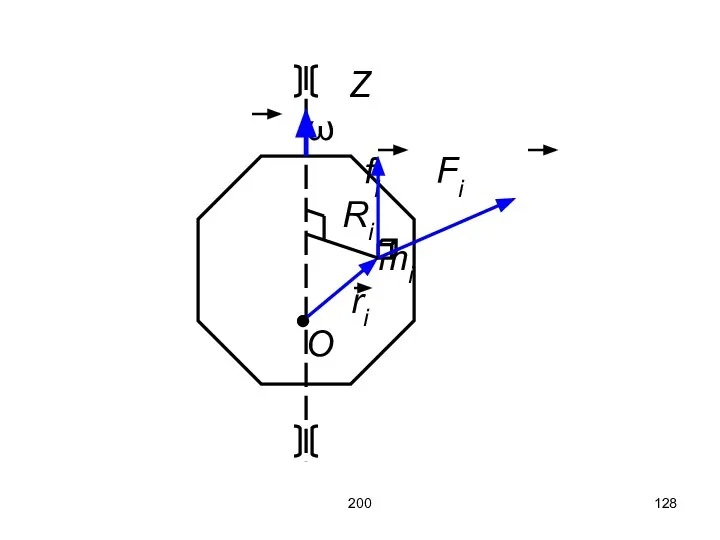
- 127. 200 Получим выражение для кинетической энергии вращающегося тела. Рассмотрим вращение тела вокруг неподвижной оси Z. Линейная
- 128. 200 Z ω fi Fi Ri mi ri O
- 129. 200 Кинетическая энергия элементарной массы mi: Кинетическая энергия всего тела:
- 130. 200 Рассмотрим силы, действующие на элементарную массу mi: внешние Fi, внутренние fi (эти силы перпендикулярны оси
- 131. 200 С другой стороны, работа внешних сил идёт на приращение кинетической энергии вращения:
- 132. 200 Так, мяч или обруч, брошенный горизонтально без вращения, раскрутится. Кинетическая энергия вращения получится за счёт
- 133. 200 И наоборот, раскрученный обруч, опущенный на горизонтальную опору, приобретёт горизонтальную скорость за счёт работы силы
- 134. 200 Теперь вычислим кинетическую энергию, поступательную и вращательную при плоском движении. Скорость i-й элементарной массы ʋ0
- 135. 200 Получим выражение для кинетической энергии твёрдого тела:
- 136. 200 Отметим следующее: Ri – расстояние от точки с массой mi до оси вращения. Запишем кинетическую
- 137. 200 здесь Σmi = m – масса всего тела, если в качестве точки О взять центр
- 138. 200 В итоге получили выражение кинетической энергии поступательного и вращательного движения (ось вращения проходит через центр
- 139. 200
- 140. 200 19. Основной закон динамики вращательного движения твёрдого тела. Момент инерции, его свойства. Теорема Штейнера (теорема
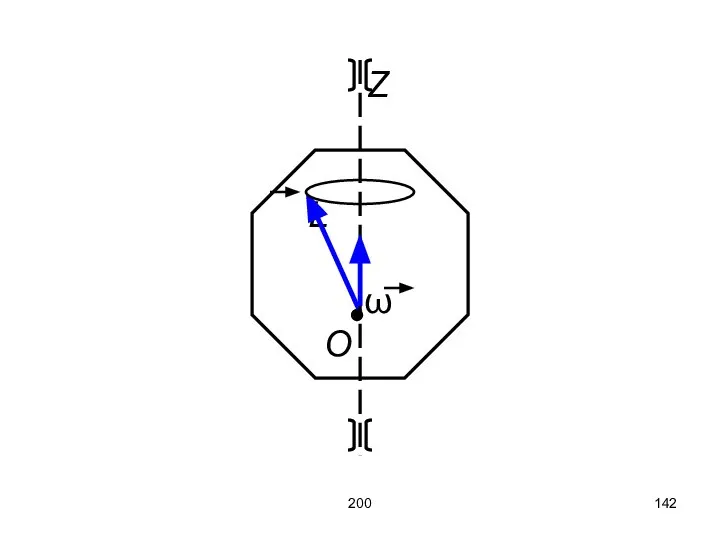
- 141. 200 Рассмотрим вращение тела вокруг неподвижной оси В общем случае вектор L не совпадает по направлению
- 142. 200 Z L ω O
- 143. 200 В случае однородного тела, симметричного относительного оси вращения, момент импульса относительно точки O, лежащей на
- 144. 200 Момент инерции зависит от выбора оси. Свободная ось – ось, положение которой в пространстве остаётся
- 145. 200
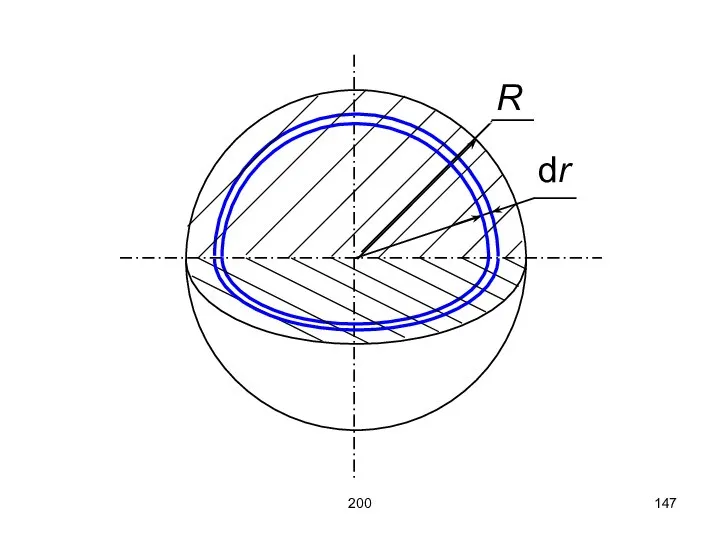
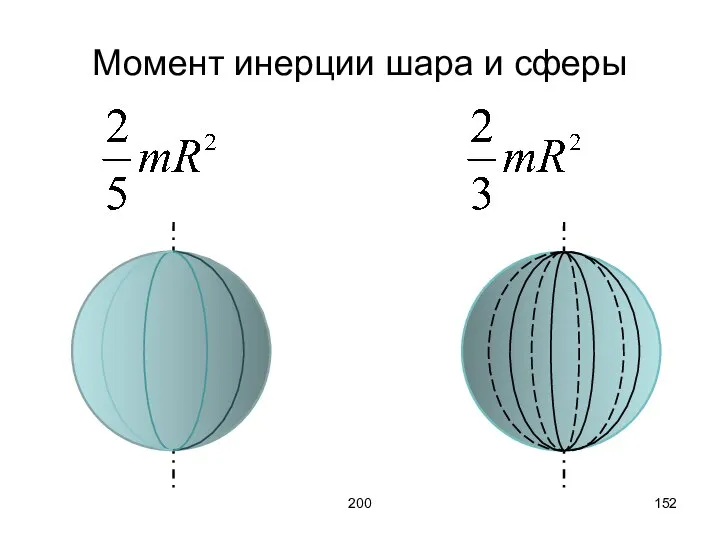
- 146. 200 Вычислим момент инерции однородного шара. Разобьём его на бесконечно тонкие сферические слои толщиной dr. Масса
- 147. 200
- 148. 200 Момент инерции шара складывается из моментов инерции сферических слоёв:
- 149. 200 Если происходит параллельный перенос оси вращения, то момент инерции увеличивается, согласно теореме Штейнера: IC –
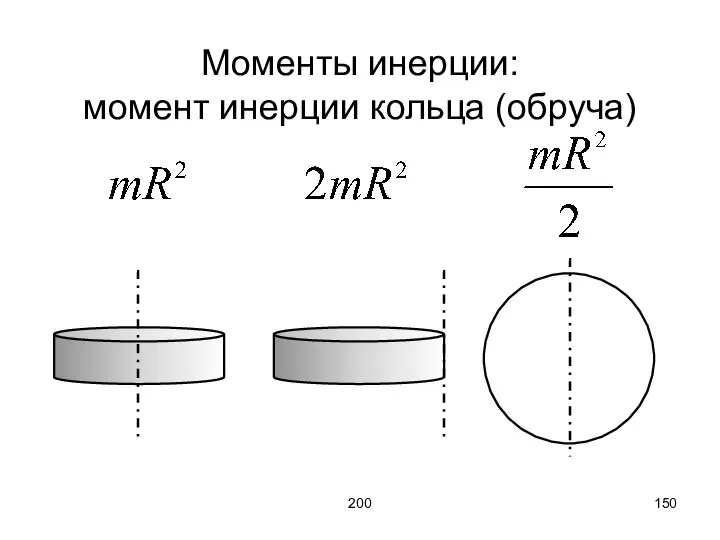
- 150. 200 Моменты инерции: момент инерции кольца (обруча)
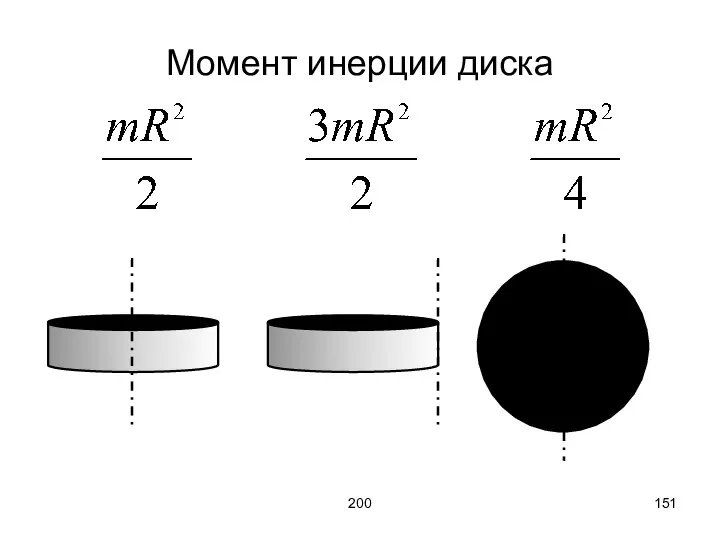
- 151. 200 Момент инерции диска
- 152. 200 Момент инерции шара и сферы
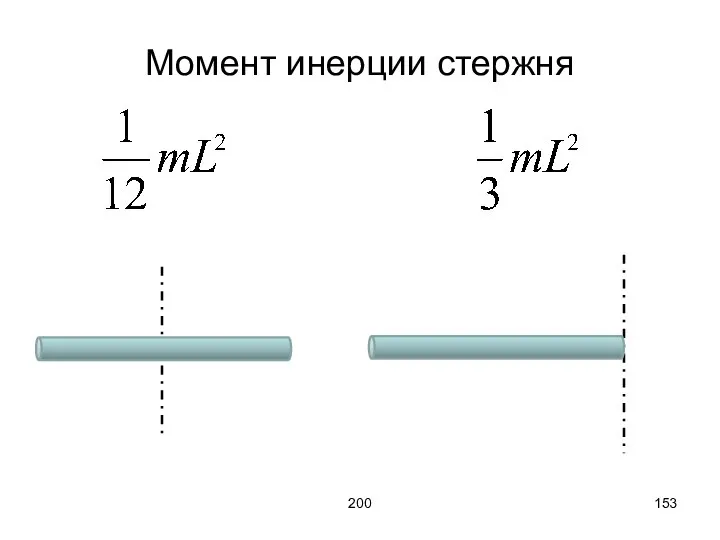
- 153. 200 Момент инерции стержня
- 154. 200
- 155. 200 20. Закон сохранения момента импульса изолированной системы. Изотропность пространства и закон сохранения момента импульса. Гироскоп.
- 156. 143 Из основного уравнения динамики вращательного движения Можно получить закон сохранения момента импульса (аналогично закону сохранения
- 157. 143 Пространство однородно, следовательно, параллельный перенос системы из одного места в другое не изменяет свойств системы
- 158. 143 Пространство изотропно, следовательно, поворот замкнутой системы как целого не отражается на её механических свойствах –
- 159. 200 Как правило, момент инерции не изменяется (I = const), следовательно, в силу закона сохранения импульса
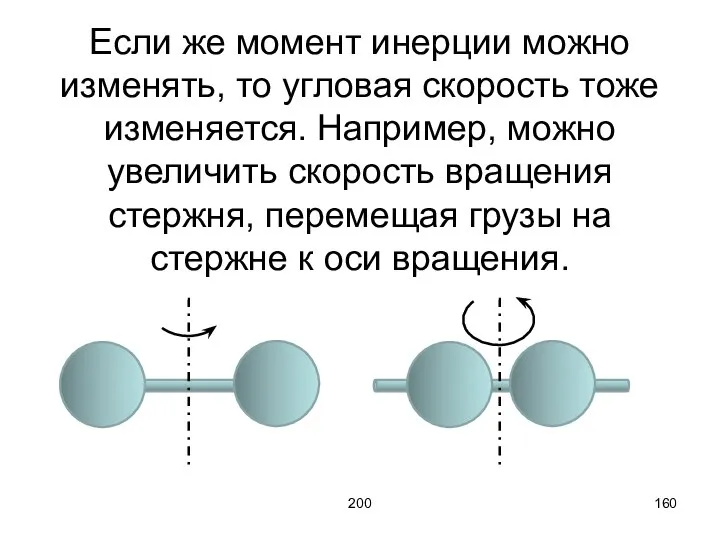
- 160. 200 Если же момент инерции можно изменять, то угловая скорость тоже изменяется. Например, можно увеличить скорость
- 161. 200 Гироскоп (волчок) – массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии (ось гироскопа).
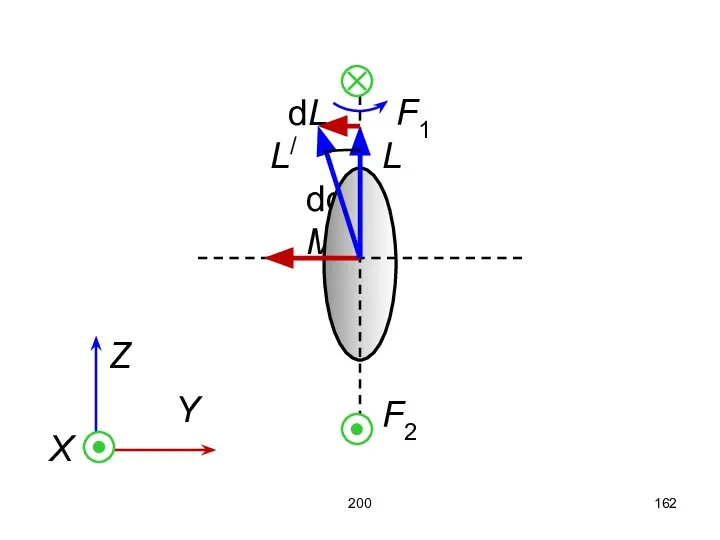
- 162. 200 dL F1 L/ L dφ M F2 Z Y X
- 163. 200 Пара сил F1 и F2 (F1 = F2) перпендикулярны плоскости рисунка (ось X), пытаются повернуть
- 164. 200 Поскольку момент импульса L был направлен вертикально вверх (ось Z), а его приращение направлено влево,
- 165. 200 В самом деле
- 166. 200 Угол поворота и угловая скорость поворота оси вращения:
- 167. 200 Момент силы, вызывающий поворот оси гироскопа, угловая скорость поворота и момент инерции связаны следующим выражением
- 168. 200 Например, волчок, раскрученный в поле тяжести Земли будет испытывать поворот оси вращения. В поле сил
- 169. 200
- 170. 200 ЛЕКЦИЯ № 7 Элементы динамики сплошных сред.
- 171. 200 ВОПРОСЫ 21. Элементы гидродинамики. Идеальная несжимаемая жидкость. Уравнение неразрывности струи. Уравнение Бернулли. Основное уравнение гидростатики.
- 172. 200
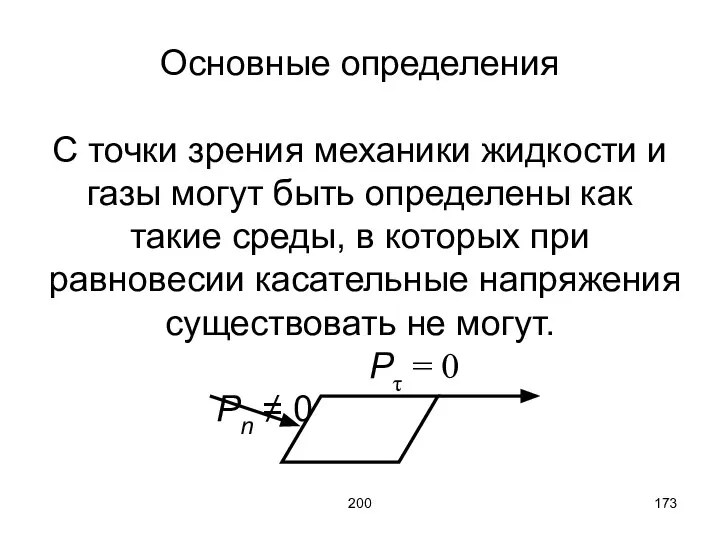
- 173. 200 Основные определения С точки зрения механики жидкости и газы могут быть определены как такие среды,
- 174. 200 Газы занимают весь предоставленный объём. Жидкость обладает собственным объёмом, который изменяется лишь незначительно с изменением
- 175. 200 Для описания движения жидкости указывают для каждой точки пространства вектор скорости как функцию времени.
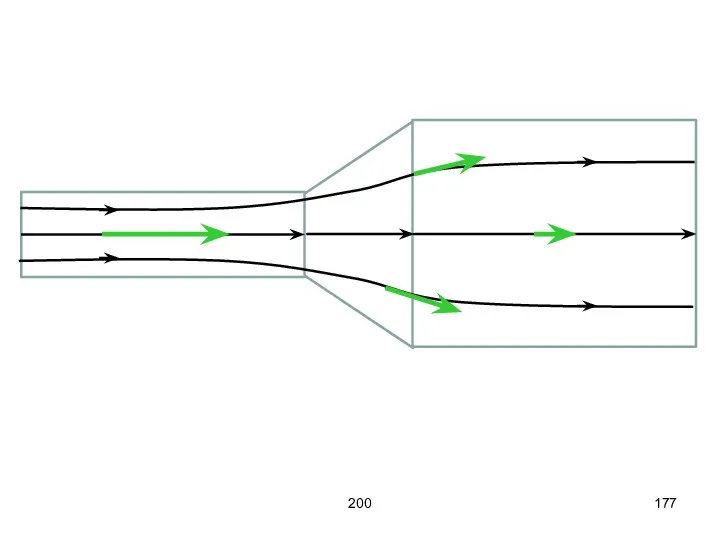
- 176. 200 Совокупность векторов ʋ, заданны для всех точек пространства, образует поле вектора скорости. Линии тока –
- 177. 200
- 178. 200 Векторные поля Градиент – вектор, направленный в сторону наибольшего изменения поля. Если каждой точке P
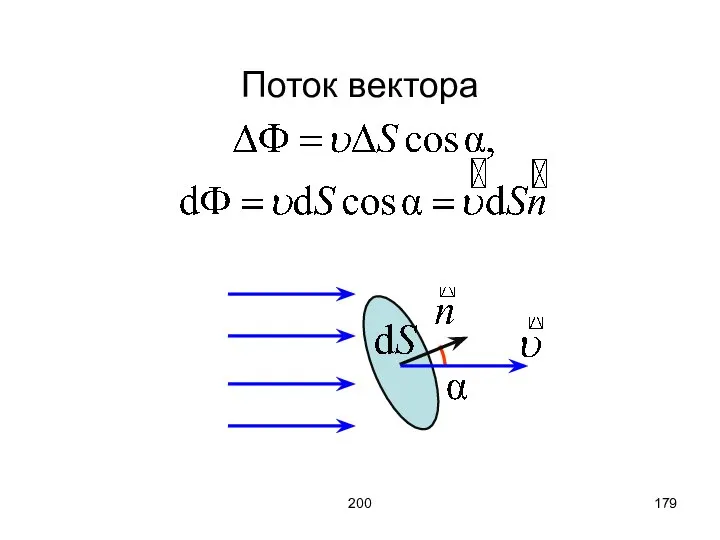
- 179. 200 Поток вектора
- 180. 200 Можно сравнить с потоком жидкости: Поток вектора «a» через поверхность S Если вектор входит в
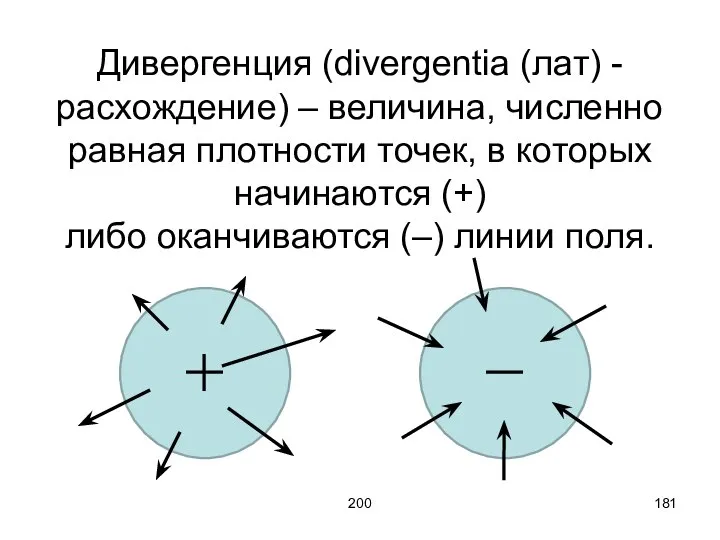
- 181. 200 Дивергенция (divergentia (лат) - расхождение) – величина, численно равная плотности точек, в которых начинаются (+)
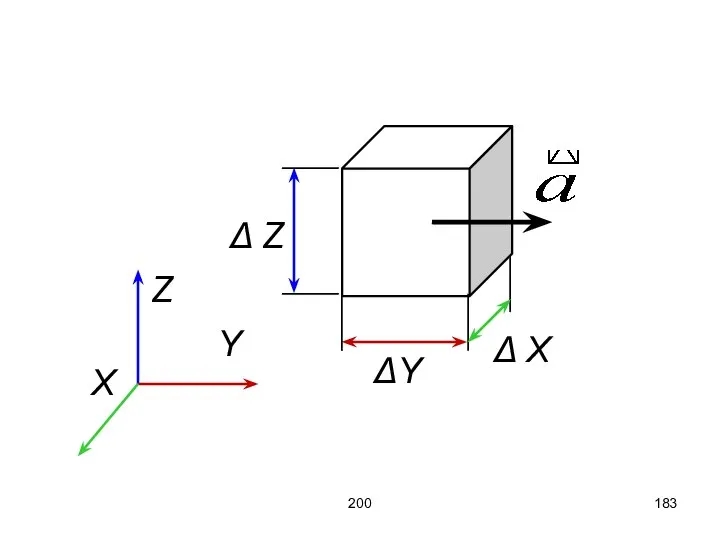
- 182. 200 Рассмотрим дивергенцию некоторой точки с точки зрения трёхмерного пространства. Выделим некоторую точку, объём которой равен
- 183. 200 Z Y X Δ Z ΔY Δ X
- 184. 200
- 185. 200 Теорема Остроградского-Гаусса (Теорема Гаусса): Поток вектора a сквозь замкнутую поверхность S равен алгебраической сумме источников
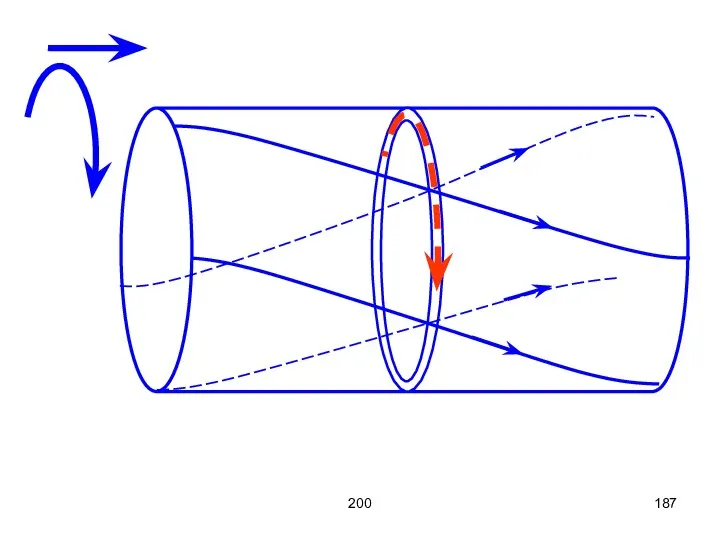
- 186. 200 Циркуляция Рассмотрим какой-нибудь канал в потоке. Если весь поток заморозить, оставить только этот канал, то
- 187. 200
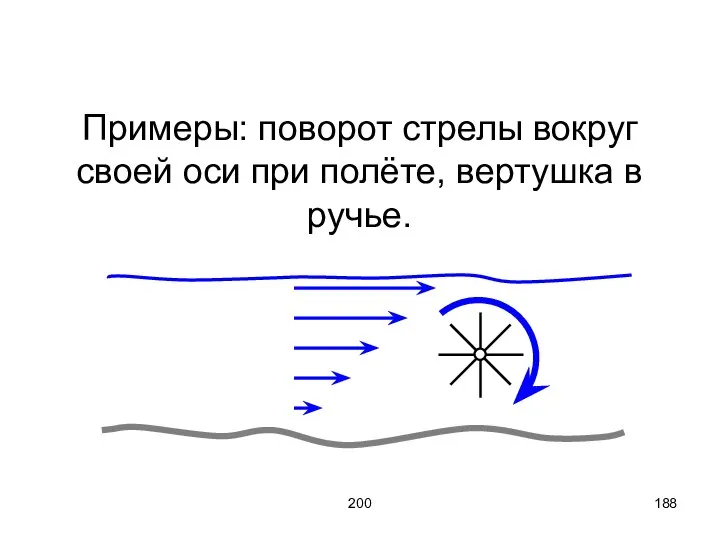
- 188. 200 Примеры: поворот стрелы вокруг своей оси при полёте, вертушка в ручье.
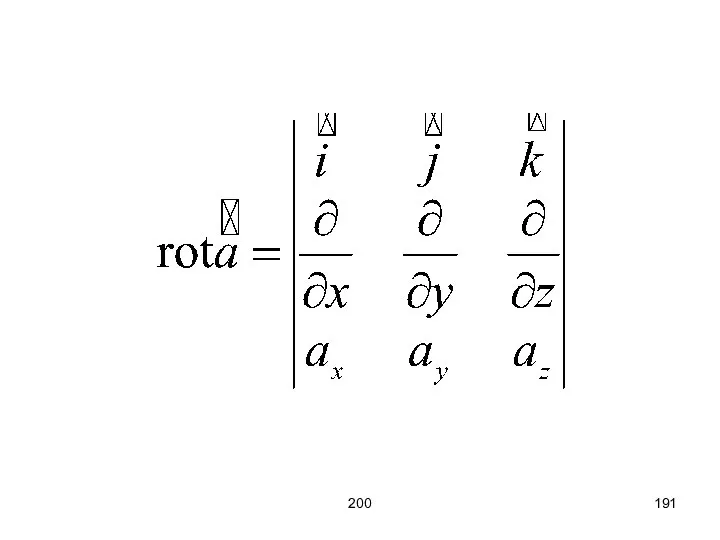
- 189. 200 Ротор – плотность порождения циркуляции.
- 190. 200
- 191. 200
- 192. 200 Теорема Стокса: Циркуляция вектора a по произвольному контуру L равна потоку вектора rota через произвольную
- 193. 200
- 194. 200 21. Элементы гидродинамики. Идеальная несжимаемая жидкость. Уравнение неразрывности струи. Уравнение Бернулли. Основное уравнение гидростатики. Уравнение
- 195. 200 Рассмотрим идеальную жидкость (жидкость, в которой внутреннее трение (вязкость) полностью отсутствует). Также, будем считать, что
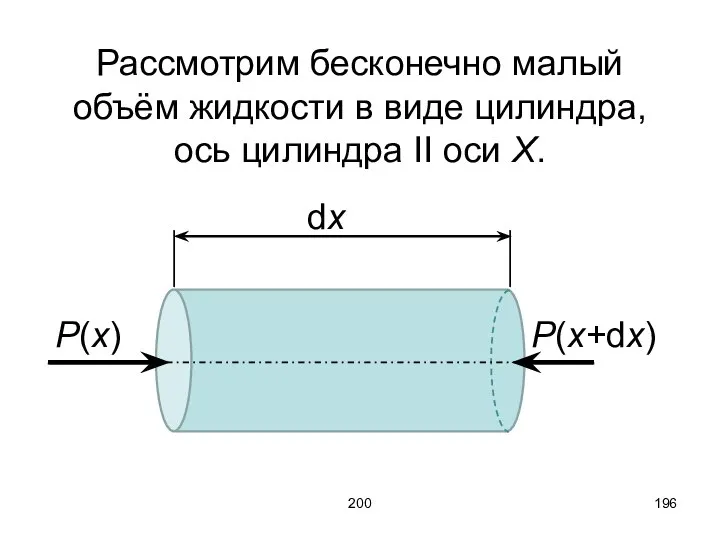
- 196. 200 Рассмотрим бесконечно малый объём жидкости в виде цилиндра, ось цилиндра II оси X. P(x+dx) dx
- 197. 200 Силы давления на боковую поверхность не учитываем, так как их проекция на ось X равна
- 198. 200 Разность в скобках можно заменить дифференциалом: – частная производная (y, z, t = const).
- 199. 200 Таким образом, на единицу объёма будут действовать сила F:
- 200. 200 В состоянии равновесия сила F (сила давления) должна уравновешиваться силой f (сила f – объёмная
- 201. 200 Основное уравнение гидростатики: Уравнение Эйлера:
- 202. 200 Основное уравнение гидростатики gradp = f, здесь p – давление жидкости, f – объёмная плотность
- 203. 200 Уравнение Эйлера здесь dV – дифференциал скорости потока жидкости, dV/dt – ускорение жидкости в данной
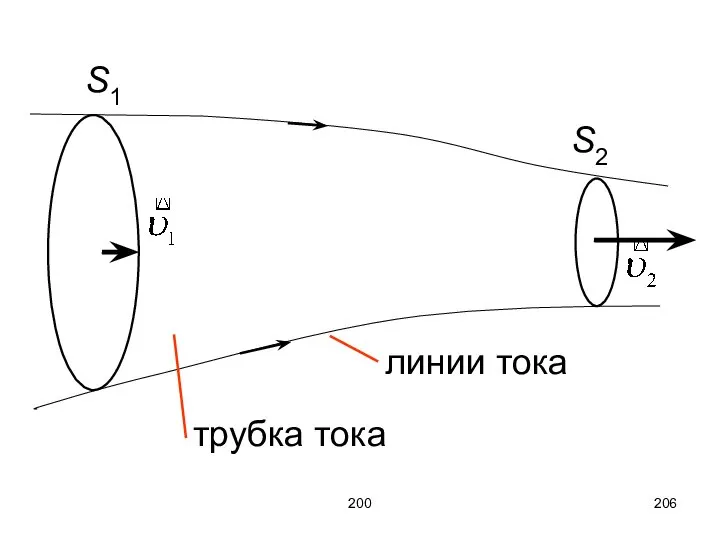
- 204. 200 Условие неразрывности жидкости Рассмотрим стационарный поток идеальной несжимаемой жидкости, рассмотрим некоторую трубку тока, ограниченную линиями
- 205. 200 Поскольку жидкость несжимаема, объём входящий равен объёму выходящему, но поперечное сечение изменяется, это приводит к
- 206. 200 линии тока трубка тока S1 S2
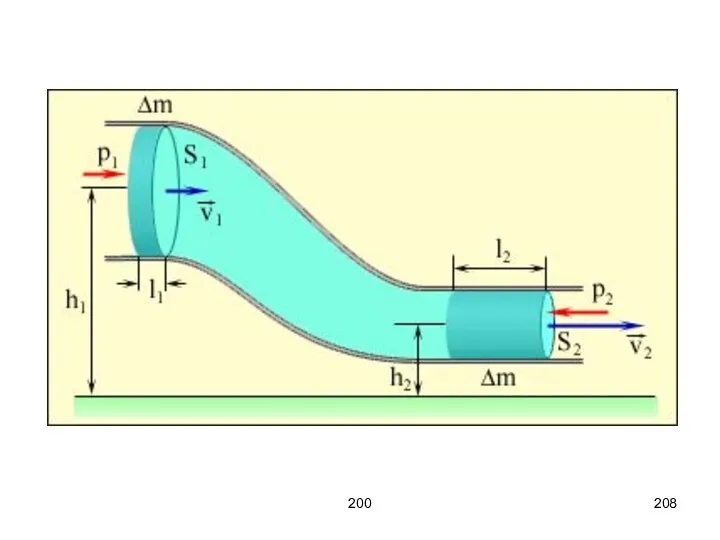
- 207. 200 Уравнение Бернулли Ещё раз рассмотрим некоторую трубку тока. В силу неразрывности ΔV1 = ΔV2 =
- 208. 200
- 209. 200 Так как нет сил трения, то приращение энергии выделенного объёма равно: и работа сил давления
- 210. 200 Приравниваем ΔE и A, делим на ΔV, получаем уравнение Бернулли:
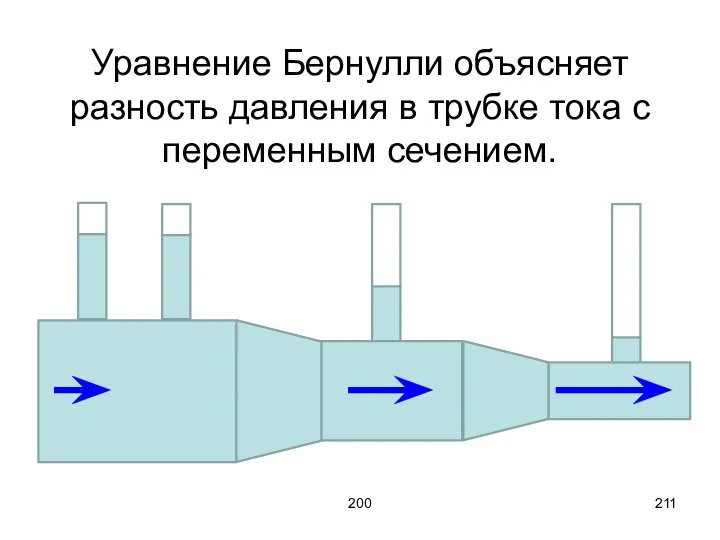
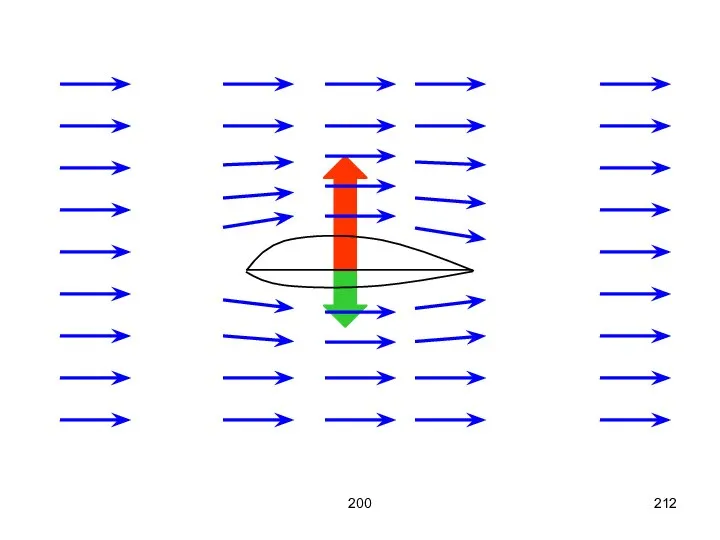
- 211. 200 Уравнение Бернулли объясняет разность давления в трубке тока с переменным сечением.
- 212. 200
- 213. 200
- 214. 200 22. Течение вязкой несжимаемой жидкости в трубе. Формула Пуазейля. Ламинарное и турбулентное течение.
- 215. 200 Рассмотрим две плоские пластины, S – площадь пластинок, ℓ – длина пластинок, d – расстояние
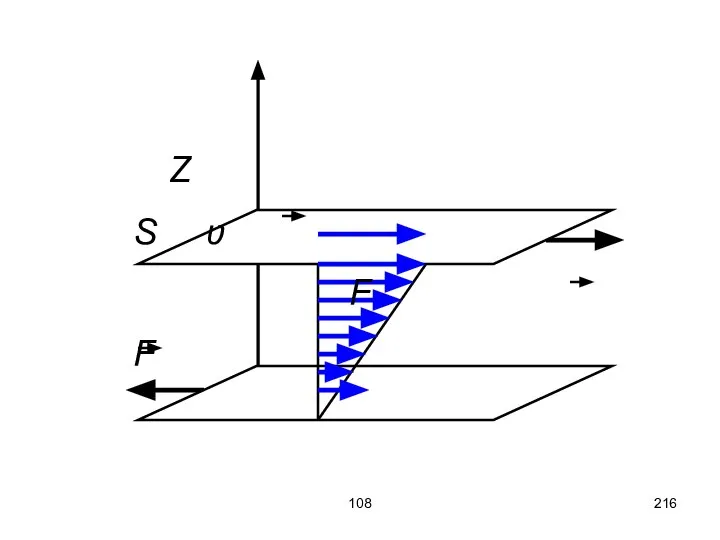
- 216. 108 Z S ʋ F F
- 217. 108 Сила передаётся за счёт трения между слоями жидкости (вязкое трение) η – коэффициент вязкости или
- 218. 200 Стационарное течение вязкой жидкости Ламинарное течение – течение жидкости как бы отдельными слоями, которые не
- 219. 200 При течении в трубе (радиус трубы R) в центре трубы (r = 0) скорость максимальна
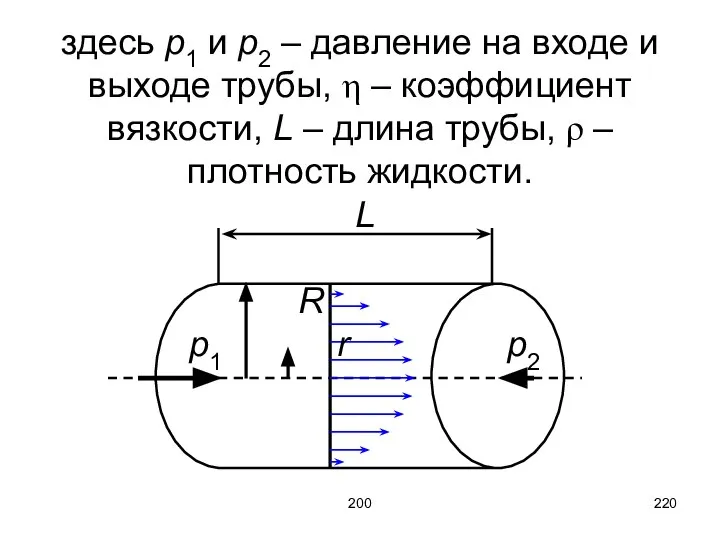
- 220. 200 здесь p1 и p2 – давление на входе и выходе трубы, η – коэффициент вязкости,
- 221. 200 Поток жидкости через трубу за одну секунду (формула Пуазейля)
- 222. 200 Формула Пуазейля справедлива для ламинарного течения. Если число Рейнольдса меньше определённого значения, то течение жидкости
- 224. Скачать презентацию





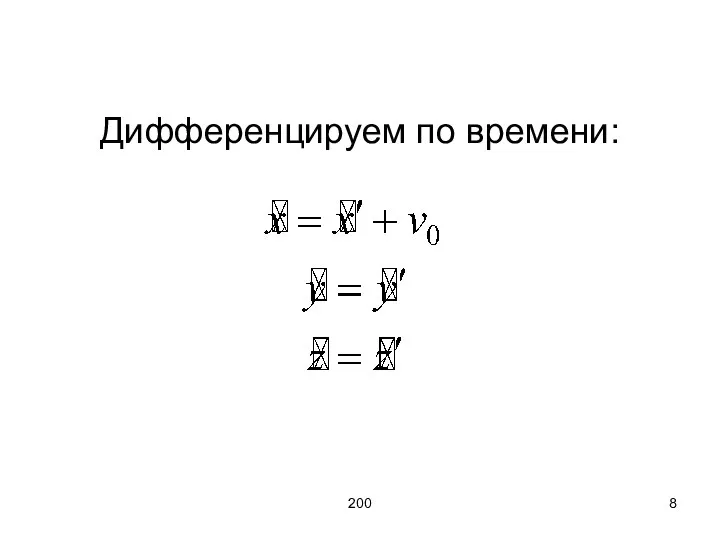
















































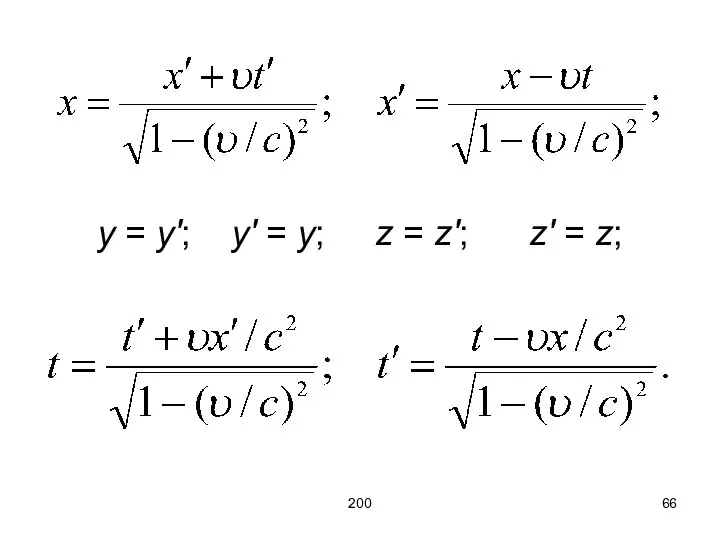






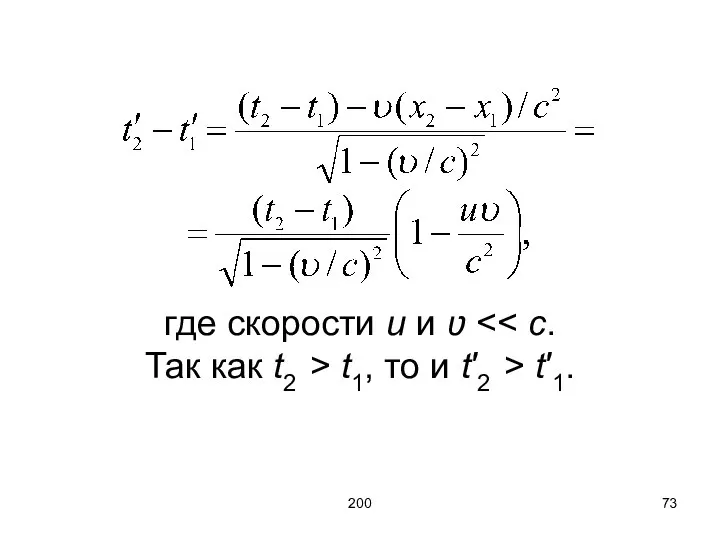



















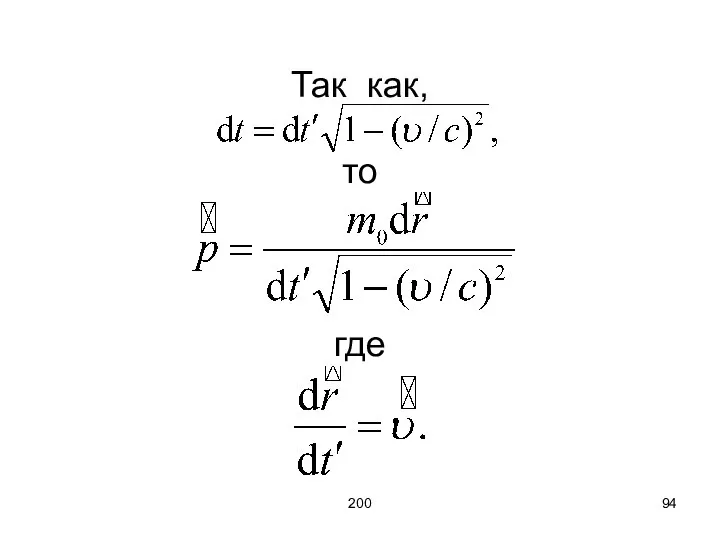



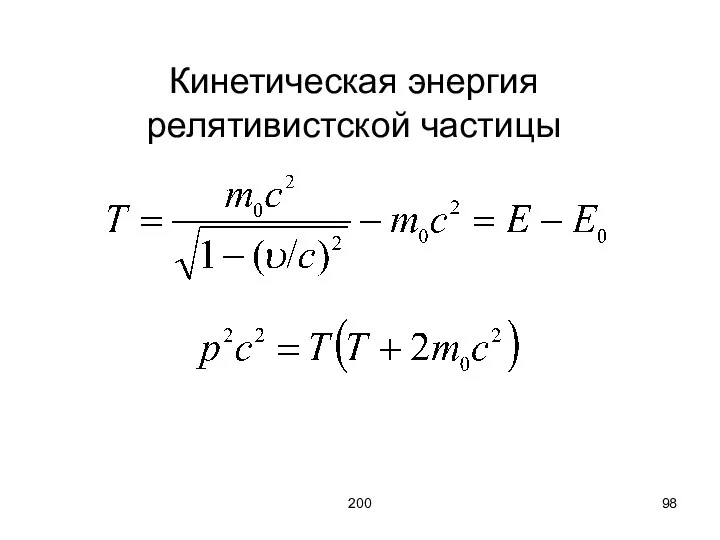




















































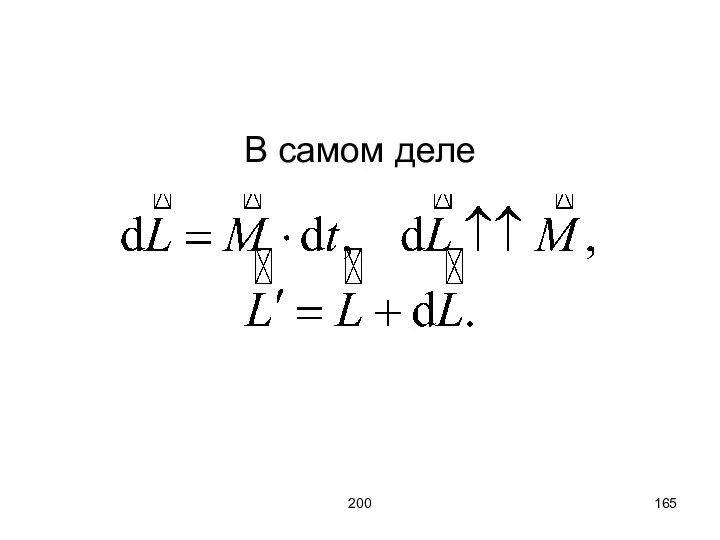













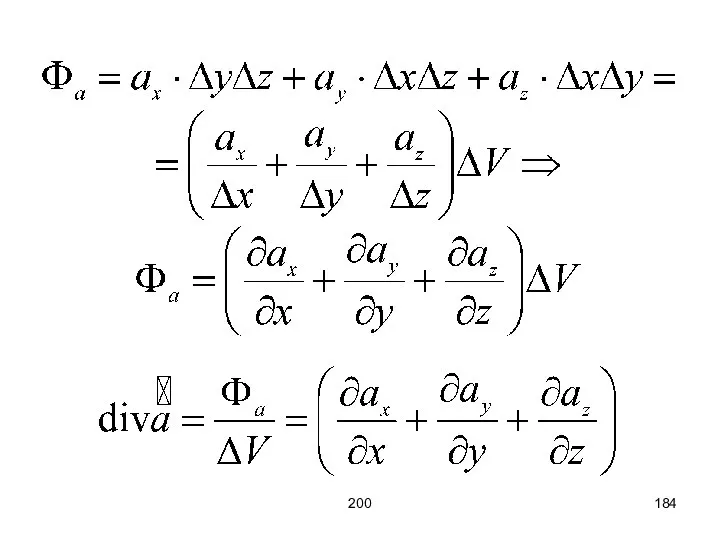



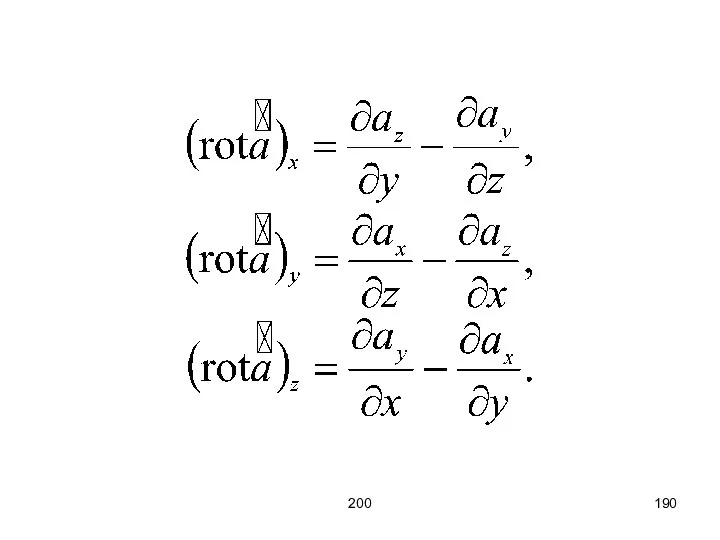
























 Интенсивность звука в идеальной жидкости
Интенсивность звука в идеальной жидкости Презентация по физике "Основное уравнение МКТ" - скачать
Презентация по физике "Основное уравнение МКТ" - скачать  Аттестационная работа. Бурение нефтяных и газовых скважин. Методика расчета утяжеленных бурильных труб
Аттестационная работа. Бурение нефтяных и газовых скважин. Методика расчета утяжеленных бурильных труб УФ-спектроскопия. Часть 1
УФ-спектроскопия. Часть 1 Презентация по физике "закон Кулона" - скачать
Презентация по физике "закон Кулона" - скачать  Презентация по физике "Использование нетрадиционного источника энергии в работе ветродвигателя" - скачать
Презентация по физике "Использование нетрадиционного источника энергии в работе ветродвигателя" - скачать  Качество изображения астрономических объективов и изображений математически-смоделированного точечного источника
Качество изображения астрономических объективов и изображений математически-смоделированного точечного источника Дисперсія світла
Дисперсія світла Инерция (7 класс) - Презентация по физике
Инерция (7 класс) - Презентация по физике Законы постоянного тока
Законы постоянного тока Второй закон термодинамики. Энтропия. (Лекция 3)
Второй закон термодинамики. Энтропия. (Лекция 3) Александр Степанович Попов – творец «русского» радио
Александр Степанович Попов – творец «русского» радио Презентация к работе «Воздействие музыкального звука разных частот на растения» Автор: Еретина Валентина, 9 «а» класс лицея-инте
Презентация к работе «Воздействие музыкального звука разных частот на растения» Автор: Еретина Валентина, 9 «а» класс лицея-инте МОБІЛЬНИЙ ЗВ’ЯЗОК Основні поняття Статистичні дані Принцип дії Вплив випромінювання Ситуація в Україні
МОБІЛЬНИЙ ЗВ’ЯЗОК Основні поняття Статистичні дані Принцип дії Вплив випромінювання Ситуація в Україні  Колебательный контур. Свободные и вынужденные электромагнитные колебания.
Колебательный контур. Свободные и вынужденные электромагнитные колебания.  Тепловые двигатели. История создания. Устройство. Принцип действия. Коэффициент полезного действия
Тепловые двигатели. История создания. Устройство. Принцип действия. Коэффициент полезного действия Методы измерения плотности материалов
Методы измерения плотности материалов Оптические методы анализа. Введение. Рефрактометрический анализ
Оптические методы анализа. Введение. Рефрактометрический анализ Тема урока: «Давление газа»
Тема урока: «Давление газа» Лекция 21 (4). Корпускулярно-волновой дуализм. Уравнение Шрёдингера
Лекция 21 (4). Корпускулярно-волновой дуализм. Уравнение Шрёдингера Электромагниттік өріс
Электромагниттік өріс CVVT System (Continuously Variable Valve Timing – Постоянно изменяемые фазы газораспределения)
CVVT System (Continuously Variable Valve Timing – Постоянно изменяемые фазы газораспределения) Диагностирование, техническое обслуживание и ремонт ходовой части ГАЗ 3307
Диагностирование, техническое обслуживание и ремонт ходовой части ГАЗ 3307 Электрическая свеча Ябочкова
Электрическая свеча Ябочкова Фізика 9 кл. магнітні явища
Фізика 9 кл. магнітні явища Рентгеновские лучи
Рентгеновские лучи Статистические и термодинамические свойства макросистем
Статистические и термодинамические свойства макросистем Формирование учебно-познавательных компетенций при решении физических задач
Формирование учебно-познавательных компетенций при решении физических задач