Содержание
- 2. Принцип неопределенности Наличие волновых свойств у микрочастиц вносит ограничения на применимость понятий класси-ческой физики. Обратимся снова
- 3. Соотношения неопределенности Математическим выражением принципа неопределенности являются соотношения неопределенности, полученные впервые Гейзенбергом (Heisenberg W., 1927 г,
- 4. Действительно, если бы частица имела одновременно определенное значение координаты и импульса, то в следующий момент времени
- 5. Соотношения неопределенностей (8.1) можно получить из формулы (7.8), которая связывает ширину волнового пакета Δx (в пределах
- 6. Вывод соотношений неопределенности из эксперимента Пусть на экран со щелью шири- ной a падает поток электронов
- 7. Вывод соотношений неопределенности из эксперимента Это означает, что после прохожде- ния щели компонента импульса px перестала
- 8. Соотношение неопределенности для энергии Учитывая, что ∆p = F∆t и ∆E = F∆x, находим: ∆p∆x =
- 9. Ширина спектральных линий В качестве примера рассмотрим вопрос об естест-венной ширине спектральных линий. Опыт пока-завает, что
- 10. Оценка размеров и энергии атома водорода С помощью соотношений неопределенности сде-лаем оценку размеров и энергии атома
- 11. Оценим расстояние, на котором электрон может быть обнаружен с наибольшей вероятностью. Со-гласно соотношению неопределенности ∆p∆R ~
- 12. Состояние атома наиболее устойчиво при минима-льном значении энергии, соответствующее рассто-яние R0 и есть наиболее вероятное. Чтобы
- 14. Скачать презентацию











 Механика двигателя V6 TDI
Механика двигателя V6 TDI Молниезащита. Принцип действия и методика расчета
Молниезащита. Принцип действия и методика расчета Қыздыру үдерістері
Қыздыру үдерістері Внутренняя энергия и способы ее изменения
Внутренняя энергия и способы ее изменения Изоляторы ЛЭП. Линейные изоляторы
Изоляторы ЛЭП. Линейные изоляторы Теорія Великого вибуху
Теорія Великого вибуху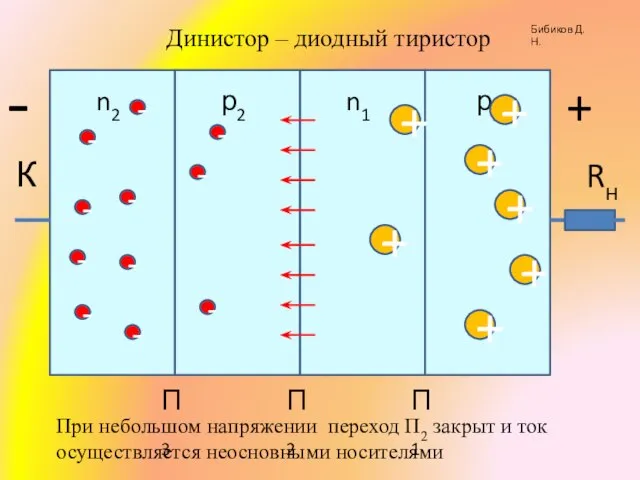 Презентация по физике "Тиристоры" - скачать
Презентация по физике "Тиристоры" - скачать  Презентация по физике "Уравнение состояния идеального газа" - скачать
Презентация по физике "Уравнение состояния идеального газа" - скачать  Постоянные магниты. Источники магнитного поля. Элетромагниты
Постоянные магниты. Источники магнитного поля. Элетромагниты Энтропия. Второе и третье начала термодинамики
Энтропия. Второе и третье начала термодинамики Классификация физических явлений
Классификация физических явлений Реакторная установка с реактором ВВЭР-1000
Реакторная установка с реактором ВВЭР-1000 Презентация по физике "Волновая оптика в задачах повышенного уровня" - скачать
Презентация по физике "Волновая оптика в задачах повышенного уровня" - скачать  Электромагнитные волны
Электромагнитные волны КПД теплового двигателя
КПД теплового двигателя Выталкивающая сила. Закон Архимеда
Выталкивающая сила. Закон Архимеда Реши анаграмму
Реши анаграмму  УРОК ФИЗИКИ В 10 КЛАССЕ Лабораторная работа №3 «Опытная проверка закона Гей – Люссака» Учитель Кононов Геннадий
УРОК ФИЗИКИ В 10 КЛАССЕ Лабораторная работа №3 «Опытная проверка закона Гей – Люссака» Учитель Кононов Геннадий  Thermometers
Thermometers Кратность циркуляции. Напоры воды в опускных трубах
Кратность циркуляции. Напоры воды в опускных трубах Презентация по физике "закон Кулона" - скачать
Презентация по физике "закон Кулона" - скачать  Элементарные частицы. Квантовая хромодинамика
Элементарные частицы. Квантовая хромодинамика Общая физика
Общая физика Делимость электрического заряда. Электрон. Строение атомов
Делимость электрического заряда. Электрон. Строение атомов Идеальная (обратимая) тепловая машина, цикл Карно
Идеальная (обратимая) тепловая машина, цикл Карно Воздействие электрического тока на человека
Воздействие электрического тока на человека Прозрачная-сенсорная-емкостная панель, на основе многослойной графеновой пленки
Прозрачная-сенсорная-емкостная панель, на основе многослойной графеновой пленки Жылу энергетикада және жылу техникада жылу энергиясын қолдану
Жылу энергетикада және жылу техникада жылу энергиясын қолдану