Содержание
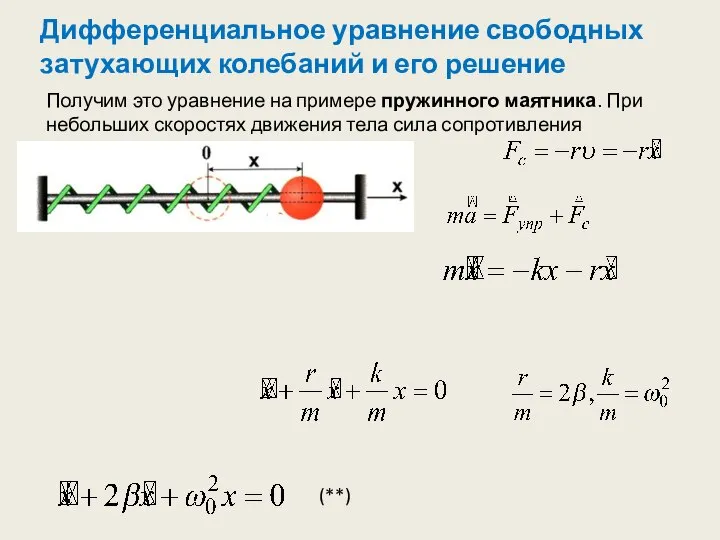
- 2. Дифференциальное уравнение свободных затухающих колебаний и его решение Получим это уравнение на примере пружинного маятника. При
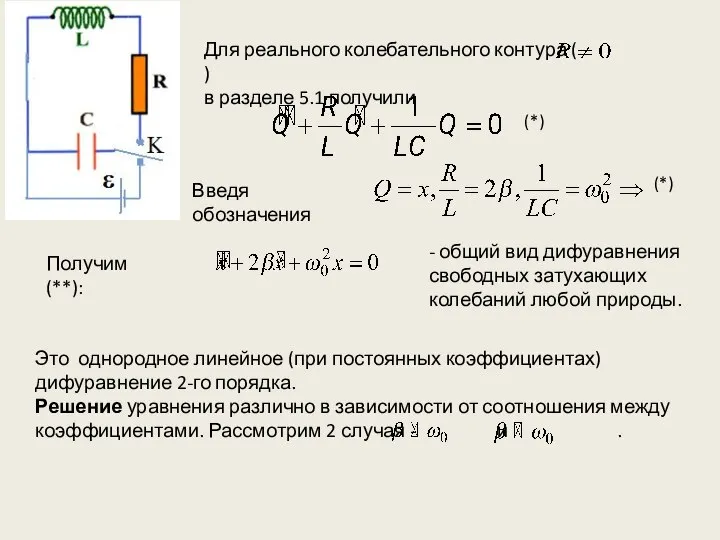
- 3. (*) Для реального колебательного контура ( ) в разделе 5.1 получили Введя обозначения (*) Получим (**):
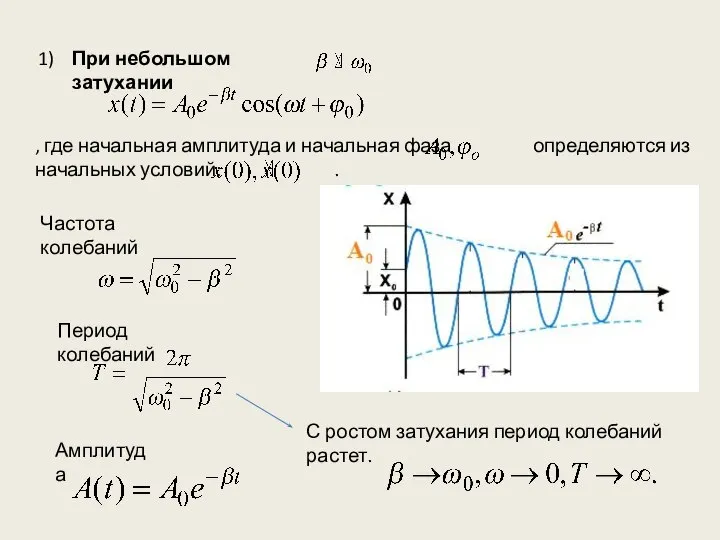
- 4. 1) , где начальная амплитуда и начальная фаза определяются из начальных условий: . При небольшом затухании
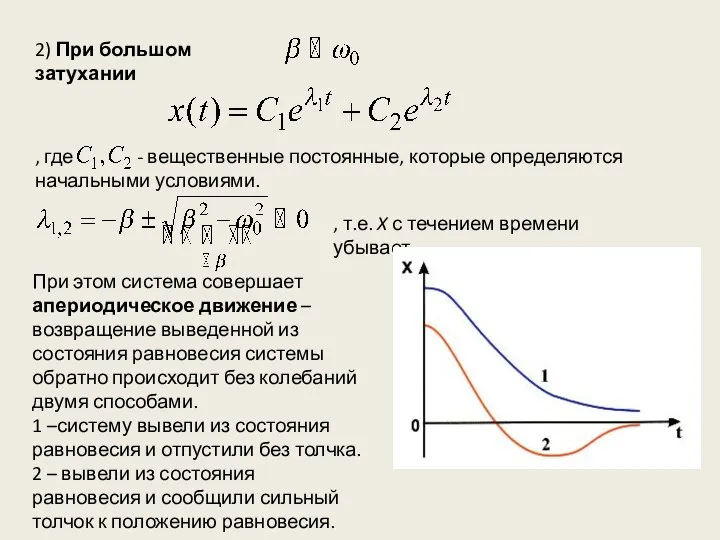
- 5. 2) При большом затухании , где - вещественные постоянные, которые определяются начальными условиями. , т.е. X
- 6. Условие, при котором затухающие колебания переходят в апериодический процесс: Для колебательного контура: -критическое сопротивление, при котором
- 7. Общие характеристики колебательной системы с затуханием 1. Коэффициент затухания β . Время релаксации τ. Рассмотрим промежуток
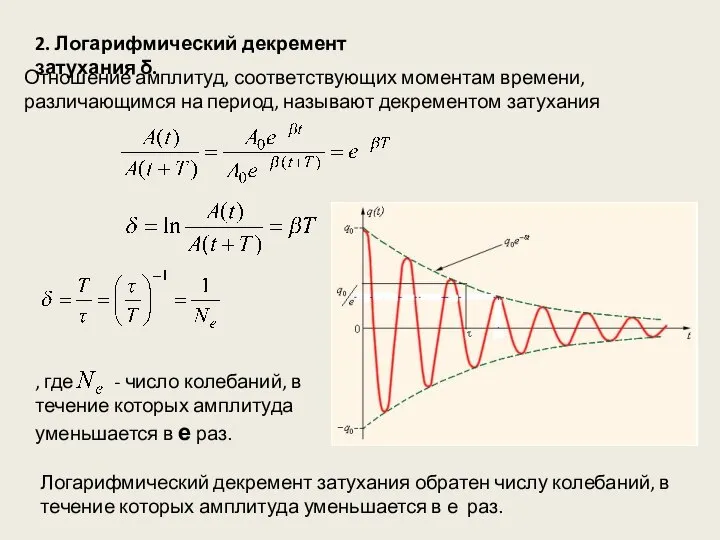
- 8. 2. Логарифмический декремент затухания δ. Отношение амплитуд, соответствующих моментам времени, различающимся на период, называют декрементом затухания
- 9. 3. Добротность колебательной системы Q. Добротность характеризует потери энергии в колебательной системе Она равна произведению на
- 10. При малом затухании колебаний : (2) (2) Добротность системы с малым затуханием пропорциональна числу колебаний, в
- 11. 5.3 Вынужденные колебания Происходят под действием внешней, периодически меняющейся со временем силы. Чтобы в реальной колебательной
- 12. - некая периодическая функция времени. Пусть, например, она меняется по гармоническому закону: Общий вид дифференциального уравнения
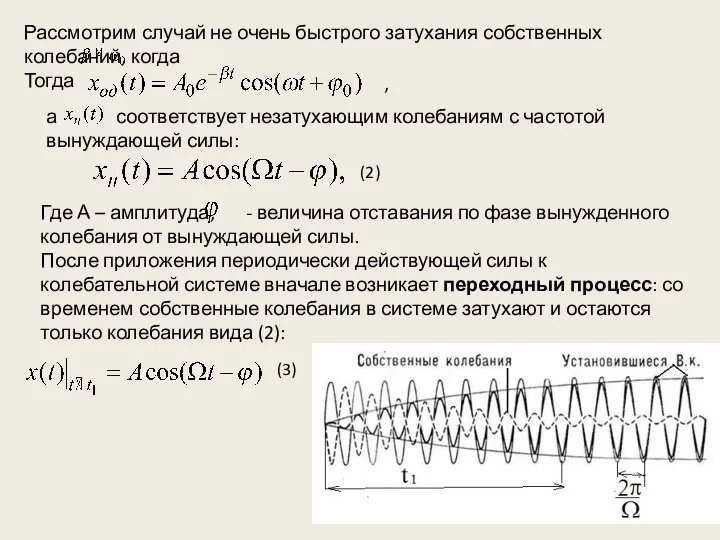
- 13. Рассмотрим случай не очень быстрого затухания собственных колебаний, когда Тогда а соответствует незатухающим колебаниям с частотой
- 14. (3) Определим и , потребовав, чтобы x(t) удовлетворял (1). А (4) (5) (3), (4), (5)⇨ (1):
- 15. Далее используем метод векторных диаграмм. Рассмотрим векторное уравнение (6) Выражение (6) – проекция на ось OX
- 16. Из прямоугольного треугольника (7) (8) Т.о. А и зависят от соотношения и , хотя вынужденные колебания
- 17. Резонанс Амплитуда вынужденных колебаний определяется выражением Зависимость амплитуды вынужденных колебаний от частоты вынуждаю- щей силы приводит
- 18. - частота вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна.
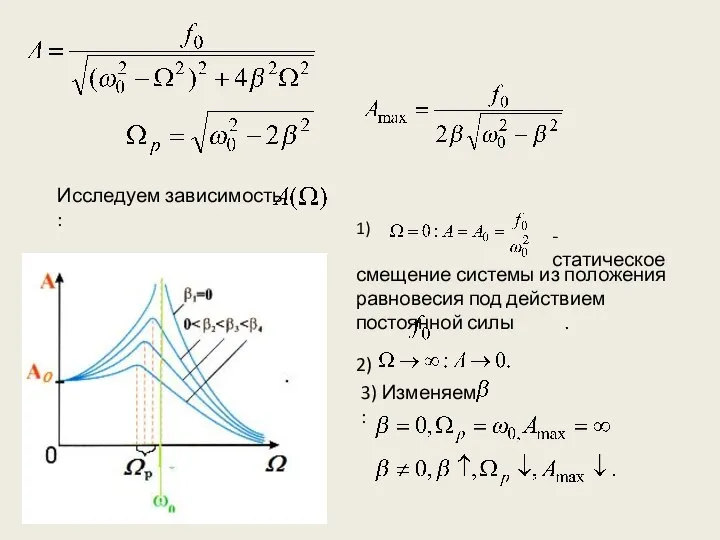
- 19. Исследуем зависимость : 1) - статическое смещение системы из положения равновесия под действием постоянной силы .
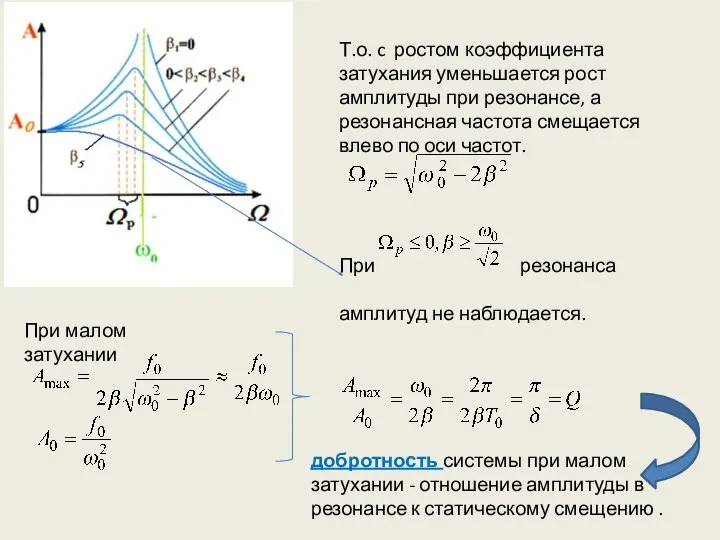
- 20. Т.о. c ростом коэффициента затухания уменьшается рост амплитуды при резонансе, а резонансная частота смещается влево по
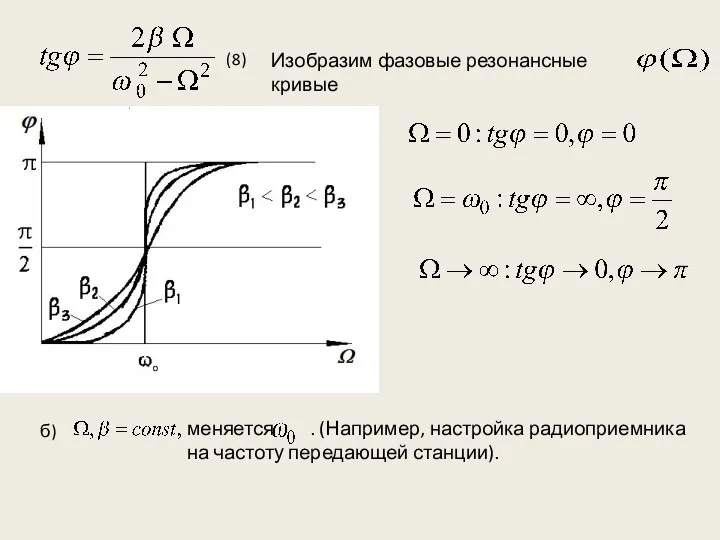
- 21. (8) Изобразим фазовые резонансные кривые б) меняется . (Например, настройка радиоприемника на частоту передающей станции).
- 23. Скачать презентацию











 Разработка услуги по установке задней пневмоподвески на автомобиль Volkswagen Multivan T6
Разработка услуги по установке задней пневмоподвески на автомобиль Volkswagen Multivan T6 Вес тела М.Н Гринченко (246-840-069) ГБСОШ № 515
Вес тела М.Н Гринченко (246-840-069) ГБСОШ № 515 Лекции по гидравлике. Введение
Лекции по гидравлике. Введение История электрификации Брянской области
История электрификации Брянской области Зубчатые передачи
Зубчатые передачи Спектроскопические методы. Лекция 7
Спектроскопические методы. Лекция 7 ГОСТ 2.770-68*. Обозначения условные графические в схемах. Элементы кинематики
ГОСТ 2.770-68*. Обозначения условные графические в схемах. Элементы кинематики Elektriska piedzina. (№2)
Elektriska piedzina. (№2)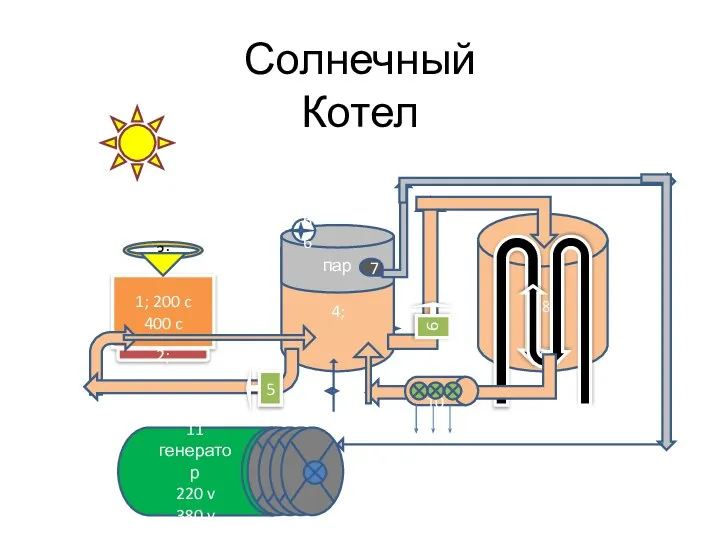 Солнечный котел
Солнечный котел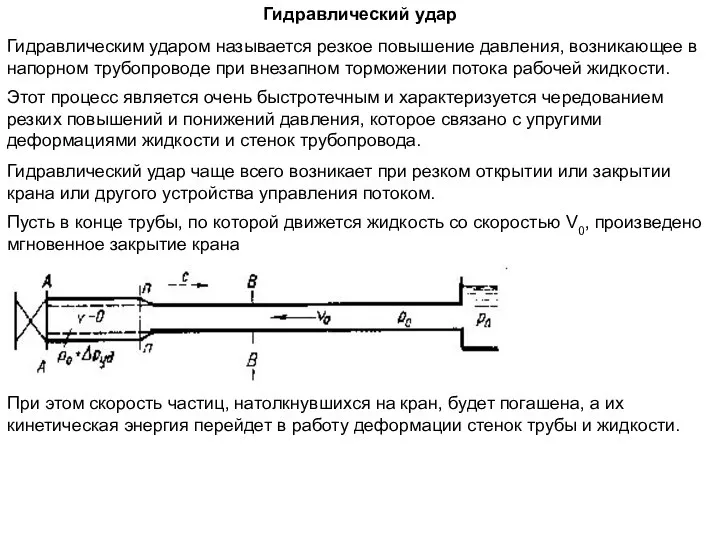 Гидравлический удар. Гидравлический таран
Гидравлический удар. Гидравлический таран Електростатика Електричний заряд. Закон збереження електричного заряду
Електростатика Електричний заряд. Закон збереження електричного заряду 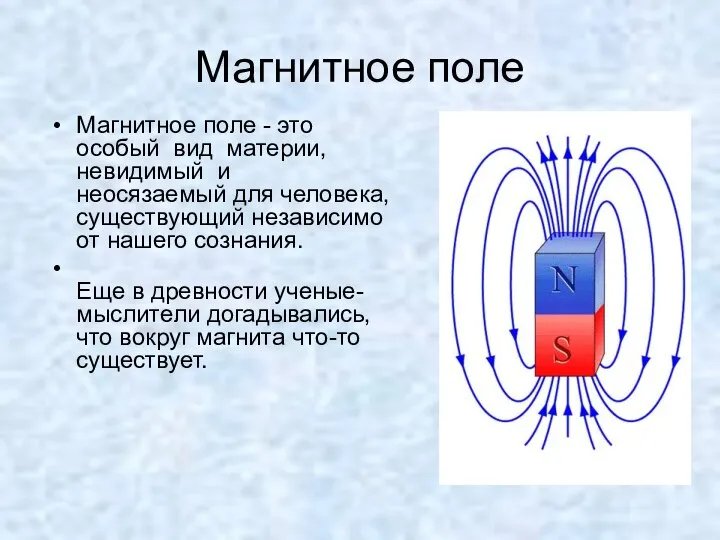 Магнитное поле Магнитное поле - это особый вид материи, невидимый и неосязаемый для человека, существующий н
Магнитное поле Магнитное поле - это особый вид материи, невидимый и неосязаемый для человека, существующий н Главные схемы электрических соединений электроустановок. (Лекция 11)
Главные схемы электрических соединений электроустановок. (Лекция 11) Измерение основных физических величин
Измерение основных физических величин Дислокации. Механизмы размножения и движения дислокаций
Дислокации. Механизмы размножения и движения дислокаций Свободные и вынужденные электромагнитные колебания
Свободные и вынужденные электромагнитные колебания Напряженность электрического поля. Принцип суперпозиций электрических полей. Силовые линии электрического поля
Напряженность электрического поля. Принцип суперпозиций электрических полей. Силовые линии электрического поля Плазма
Плазма Презентация по физике "Гидравлический пресс" - скачать
Презентация по физике "Гидравлический пресс" - скачать  «Предварительное исследование воды из разных источников.» Авторы: Елагина Мария Вадимовна 10 «б» класс МБОУ КСОШ №13 г. Новый Уре
«Предварительное исследование воды из разных источников.» Авторы: Елагина Мария Вадимовна 10 «б» класс МБОУ КСОШ №13 г. Новый Уре Конденсаторы Выполнил: Каретко Дима, ученик 10 «А» Руководитель: Попова Ирина Александровна, учитель физики Белово 2011
Конденсаторы Выполнил: Каретко Дима, ученик 10 «А» Руководитель: Попова Ирина Александровна, учитель физики Белово 2011 Ядерная физика
Ядерная физика Електричний струм у різних середовищах
Електричний струм у різних середовищах Презентація з фізики на тему: “Як акули «використовують» закон Ома» учениці 7(11)Б класу Бургелі Наталії
Презентація з фізики на тему: “Як акули «використовують» закон Ома» учениці 7(11)Б класу Бургелі Наталії  Physical chemistry of nanostructured systems
Physical chemistry of nanostructured systems Тест по физике Выполнил ученик 11 «А» класса Серый Константин
Тест по физике Выполнил ученик 11 «А» класса Серый Константин Поверки теодолита 4Т30П. Измерение углов. Лекция №7
Поверки теодолита 4Т30П. Измерение углов. Лекция №7 Расчет производительности экструдеров
Расчет производительности экструдеров