Содержание
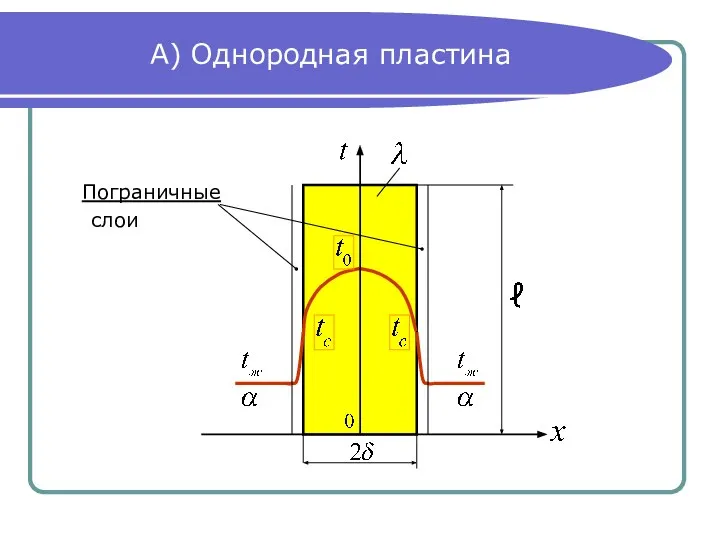
- 2. А) Однородная пластина Пограничные слои
- 3. Дифференциальное уравнение теплопроводности При бесконечная пластина. В стационарном процессе: Найти: Дифференциальное уравнение теплопроводности: (1) Для стационарного
- 4. Граничные условия Условия теплоотдачи одинаковы с обеих сторон пластины, поэтому температурное поле симметричное, а тепловыделения в
- 5. Константы интегрирования Константы интегрирования находятся из граничных условий (4) и уравнения (5) при: , (7) .
- 6. Тепловой поток и температуры Подставим константы интегрирования (7) и (12) в (6): (13) уравнение параболы. Тепловой
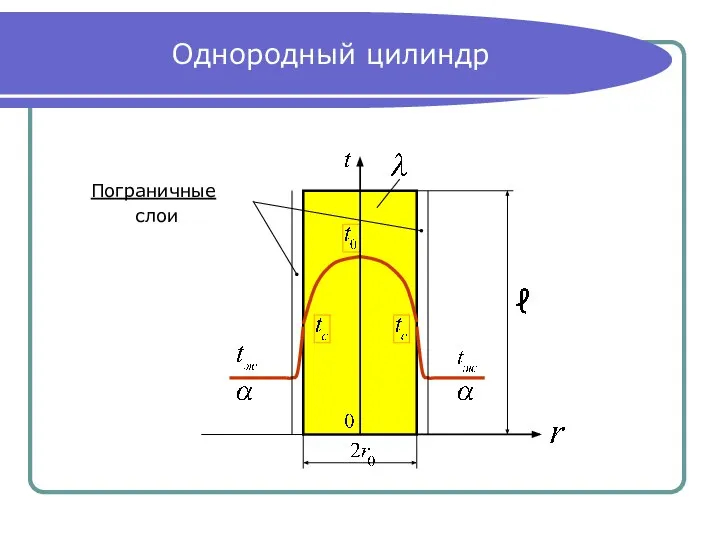
- 7. Однородный цилиндр Пограничные слои
- 8. Дифференциальное уравнение теплопроводности для цилиндра Для бесконечного цилиндрического стержня . При стационарном режиме Найти Условия теплоотдачи
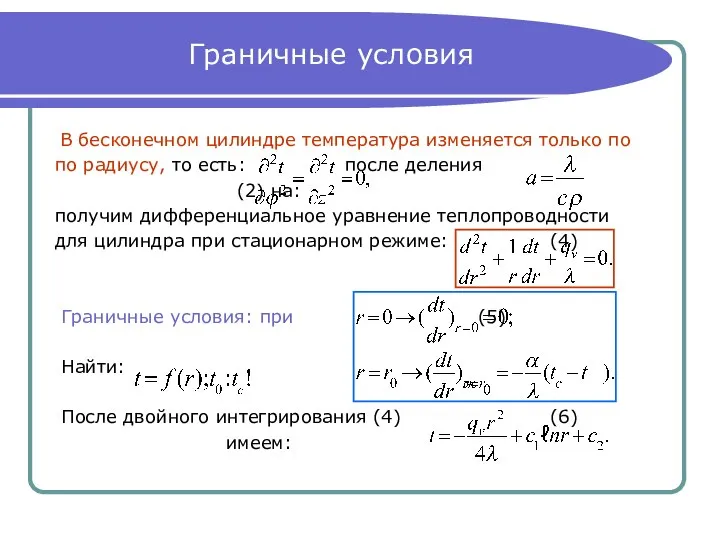
- 9. Граничные условия В бесконечном цилиндре температура изменяется только по по радиусу, то есть: после деления (2)
- 10. Конвективная теплоотдача от цилиндра к жидкости Определив константы интегрирования и подставив их в (6), имеем: (7)
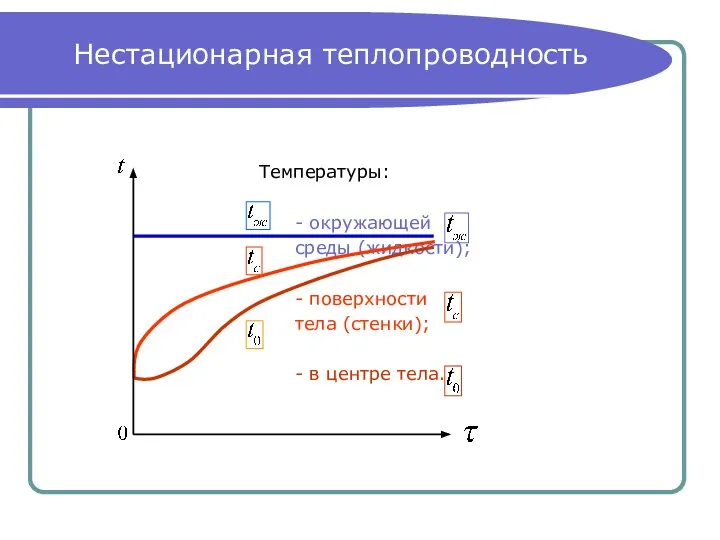
- 11. Нестационарная теплопроводность Температуры: - окружающей среды (жидкости); - поверхности тела (стенки); - в центре тела.
- 12. Дифференциальное уравнение теплопроводности Нестационарная теплопроводность имеет место при нагревании и охлаждении заготовок, пуске и отключении теплоэнергетических
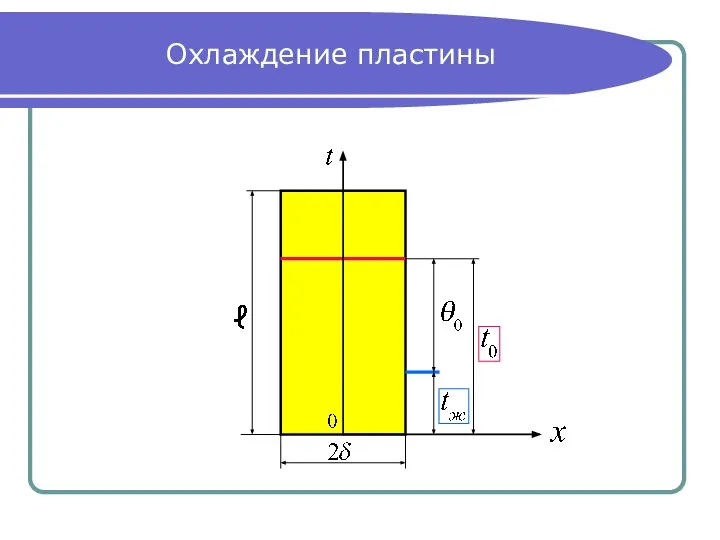
- 13. Охлаждение пластины
- 14. Начальные и граничные условия Рассматриваем охлаждение (нагревание) пластины при: Подставляем избыточную температуру пластины в дифференциальное уравнение
- 15. Разделение переменных Решение дифференциального уравнения (2) ищем в виде: произведения двух функций, из которых одна является
- 16. Решение в общем виде то есть: (7) (8) Получилась система дифференциальных уравнений (7) и (8), которой
- 17. Константы интегрирования Так как то или: При: а при Таким образом, решение надо отбросить, как не
- 18. Аналитическое решение то есть (11) После сокращения на или: Здесь число (критерий) Био – соотношение конвективной
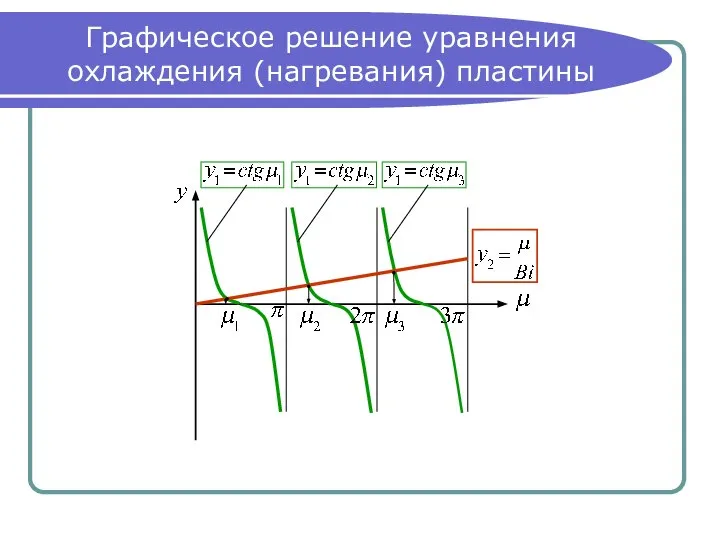
- 19. Графическое решение уравнения охлаждения (нагревания) пластины
- 20. Результаты графического решения При то есть функция совпадает с осью абсцисс, то есть: При то есть
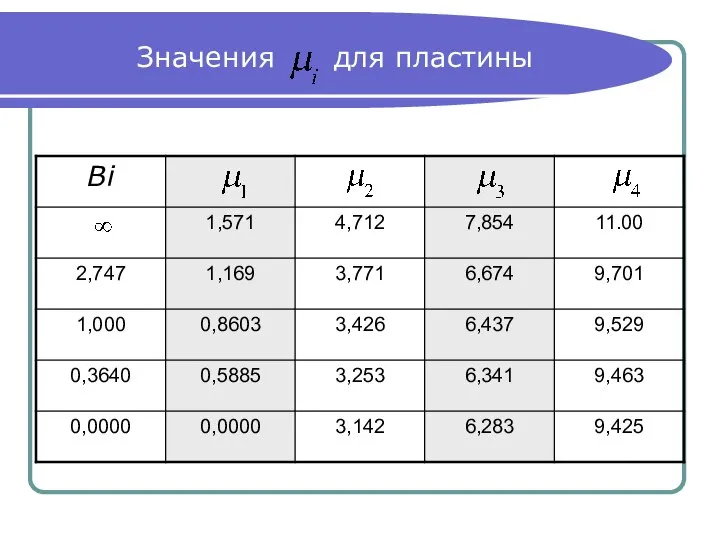
- 21. Значения для пластины
- 22. Условия на оси пластины В безразмерном виде: здесь число Fo (критерий) Фурье – безразмерное время. Для
- 23. Условия на поверхности пластины На поверхности пластины: Введем обозначение тогда: (16) Функции табулированы и могут быть
- 24. Графические решения На оси пластины: (18) На поверхности пластины: (19) Точные графики для оси пластины (Х
- 26. Скачать презентацию
















 Равновесие при наличии трения
Равновесие при наличии трения Жидкостные лазеры
Жидкостные лазеры Кинетическая энергия материальной точки и механической системы. (Лекция 6)
Кинетическая энергия материальной точки и механической системы. (Лекция 6) Теоретические основы теплотехники
Теоретические основы теплотехники Кривошипно-шатунный механизм
Кривошипно-шатунный механизм Трение не учитывать нельзя!
Трение не учитывать нельзя! Радиоволны и радио
Радиоволны и радио Устройство микроскопа
Устройство микроскопа Электризация тел при соприкосновении. Взаимодействие заряженных тел
Электризация тел при соприкосновении. Взаимодействие заряженных тел Arduino. Electrical circuit
Arduino. Electrical circuit Уравнение состояния идеального газа
Уравнение состояния идеального газа Основы слесарно-сборочных и электромонтажных работ. Правила эксплуатации и безопасности обслуживания электроустановок
Основы слесарно-сборочных и электромонтажных работ. Правила эксплуатации и безопасности обслуживания электроустановок Основы молекулярной физики
Основы молекулярной физики Основы теории антенн. Лекция № 5. АФУ
Основы теории антенн. Лекция № 5. АФУ Презентация по физике "Реактивное движение" - скачать
Презентация по физике "Реактивное движение" - скачать  Проводниковые материалы. Контактные явления. (Лекция 3.2)
Проводниковые материалы. Контактные явления. (Лекция 3.2) The influence of the radionuclide composition on the radiation characteristics of radioactive waste from Ukrainian
The influence of the radionuclide composition on the radiation characteristics of radioactive waste from Ukrainian Характеристики электрического тока
Характеристики электрического тока Физика. Введение
Физика. Введение Дисперсия
Дисперсия Традиционные источники энергии. Достоинства и недостатки Работу выполнил: ученица 10 класса Елагина М.В. 2012 год. Проверила: Васил
Традиционные источники энергии. Достоинства и недостатки Работу выполнил: ученица 10 класса Елагина М.В. 2012 год. Проверила: Васил Эхо. Световое эхо
Эхо. Световое эхо Опыт Резерфорда
Опыт Резерфорда  Неустановившееся движение жидкости. Гидравлический удар в трубопроводах. Тема № 11.2
Неустановившееся движение жидкости. Гидравлический удар в трубопроводах. Тема № 11.2 Динамика твердого тела. Момент силы. Момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения
Динамика твердого тела. Момент силы. Момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения Зависимость силы тока от напряжения
Зависимость силы тока от напряжения Колебания. Основные определения
Колебания. Основные определения Физическая картина мира. Принципы современной физики
Физическая картина мира. Принципы современной физики