Содержание
- 2. Some things you will learn in this tutorial How to learn multi-layer generative models of unlabelled
- 3. A spectrum of machine learning tasks Low-dimensional data (e.g. less than 100 dimensions) Lots of noise
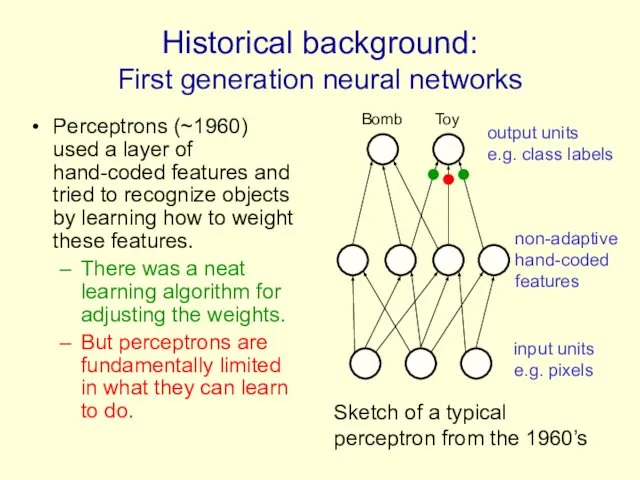
- 4. Historical background: First generation neural networks Perceptrons (~1960) used a layer of hand-coded features and tried
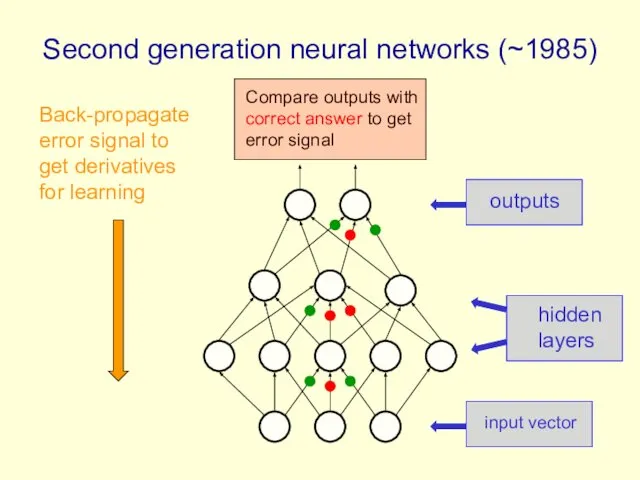
- 5. Second generation neural networks (~1985) input vector hidden layers outputs Back-propagate error signal to get derivatives
- 6. A temporary digression Vapnik and his co-workers developed a very clever type of perceptron called a
- 7. What is wrong with back-propagation? It requires labeled training data. Almost all data is unlabeled. The
- 8. Overcoming the limitations of back-propagation Keep the efficiency and simplicity of using a gradient method for
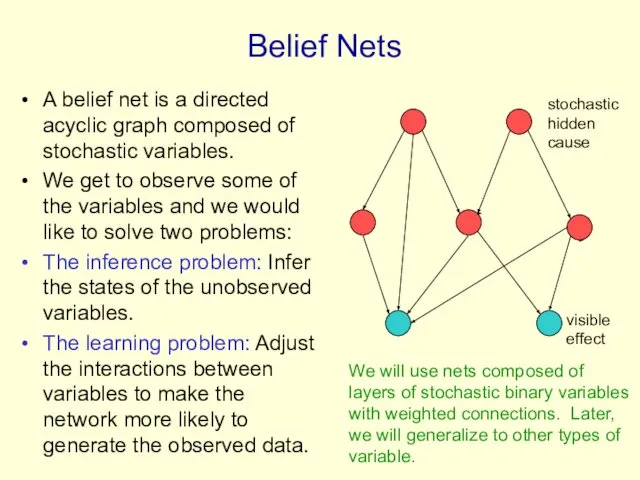
- 9. Belief Nets A belief net is a directed acyclic graph composed of stochastic variables. We get
- 10. Stochastic binary units (Bernoulli variables) These have a state of 1 or 0. The probability of
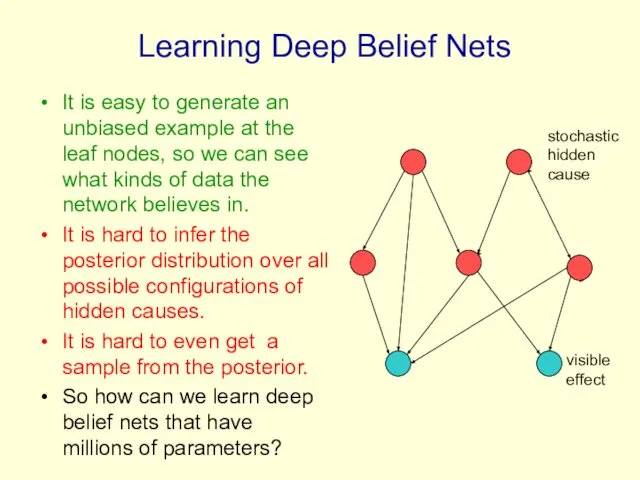
- 11. Learning Deep Belief Nets It is easy to generate an unbiased example at the leaf nodes,
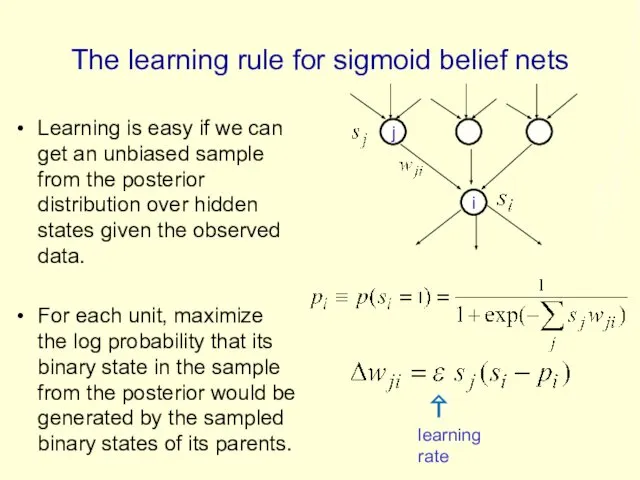
- 12. The learning rule for sigmoid belief nets Learning is easy if we can get an unbiased
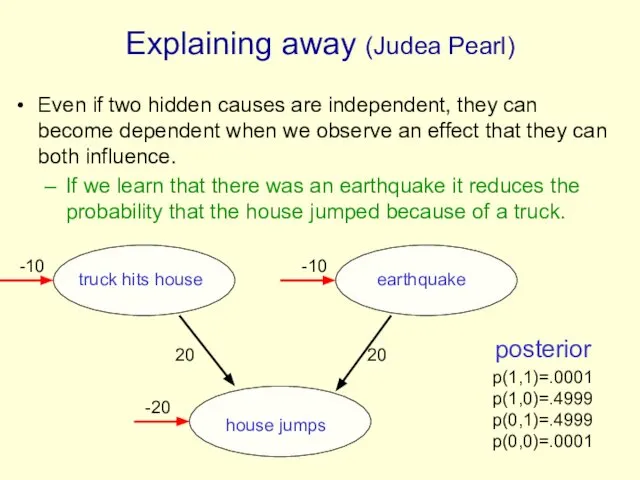
- 13. Explaining away (Judea Pearl) Even if two hidden causes are independent, they can become dependent when
- 14. Why it is usually very hard to learn sigmoid belief nets one layer at a time
- 15. Two types of generative neural network If we connect binary stochastic neurons in a directed acyclic
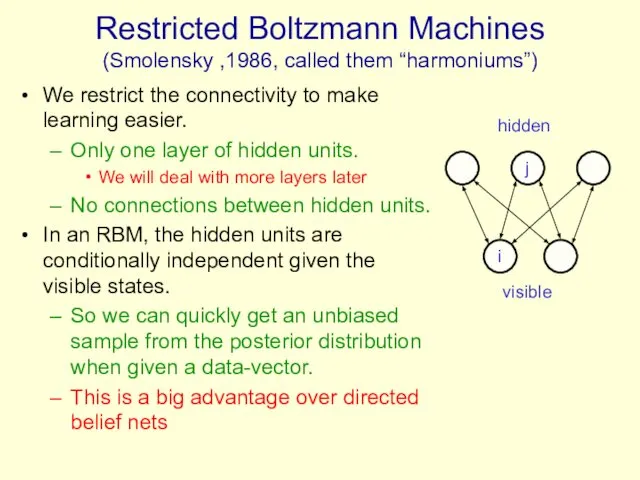
- 16. Restricted Boltzmann Machines (Smolensky ,1986, called them “harmoniums”) We restrict the connectivity to make learning easier.
- 17. The Energy of a joint configuration (ignoring terms to do with biases) weight between units i
- 18. Weights ? Energies ? Probabilities Each possible joint configuration of the visible and hidden units has
- 19. Using energies to define probabilities The probability of a joint configuration over both visible and hidden
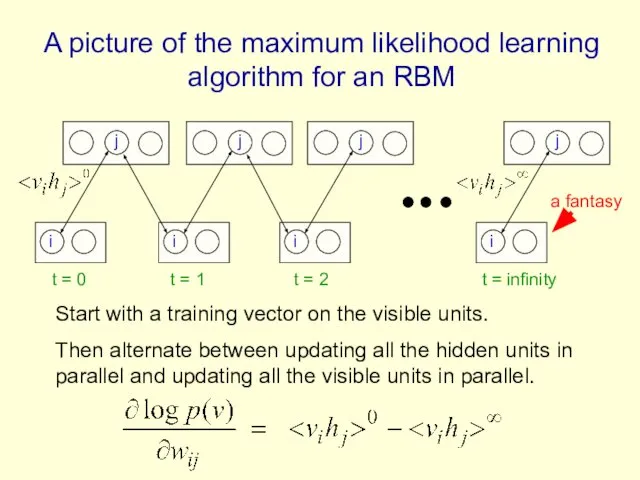
- 20. A picture of the maximum likelihood learning algorithm for an RBM i j i j i
- 21. A quick way to learn an RBM i j i j t = 0 t =
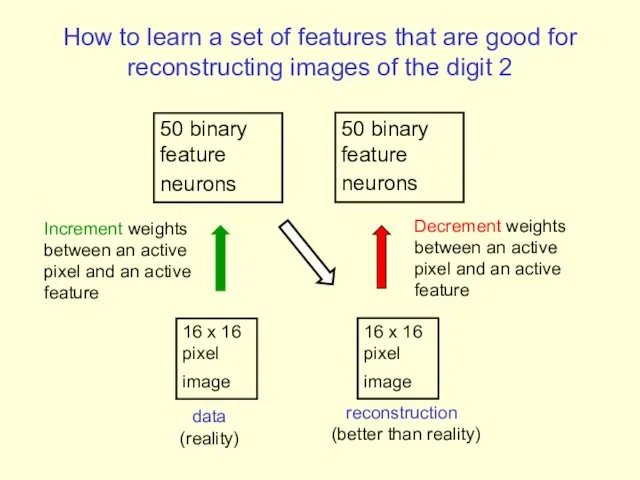
- 22. How to learn a set of features that are good for reconstructing images of the digit
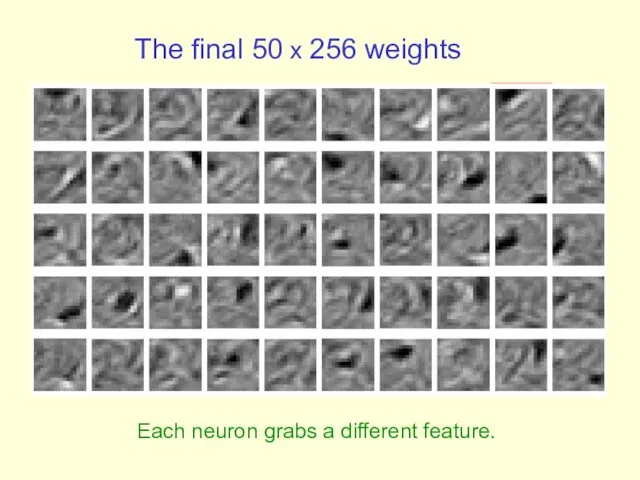
- 23. The final 50 x 256 weights Each neuron grabs a different feature.
- 24. Reconstruction from activated binary features Data Reconstruction from activated binary features Data How well can we
- 25. Three ways to combine probability density models (an underlying theme of the tutorial) Mixture: Take a
- 26. Training a deep network (the main reason RBM’s are interesting) First train a layer of features
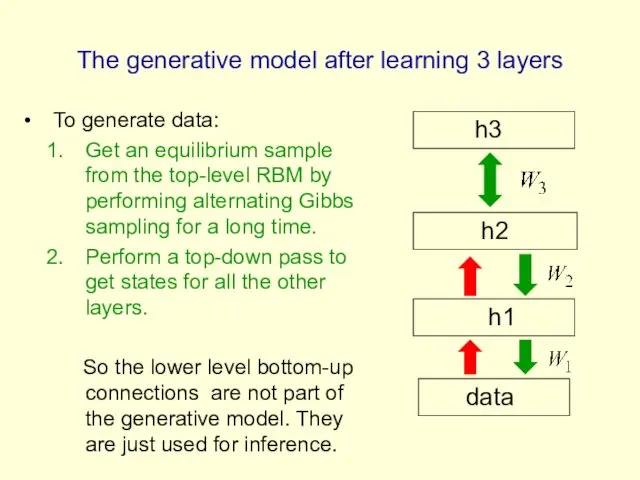
- 27. The generative model after learning 3 layers To generate data: Get an equilibrium sample from the
- 28. Why does greedy learning work? An aside: Averaging factorial distributions If you average some factorial distributions,
- 29. Why does greedy learning work? Each RBM converts its data distribution into an aggregated posterior distribution
- 30. Why does greedy learning work? The weights, W, in the bottom level RBM define p(v|h) and
- 31. Which distributions are factorial in a directed belief net? In a directed belief net with one
- 32. Why does greedy learning fail in a directed module? A directed module also converts its data
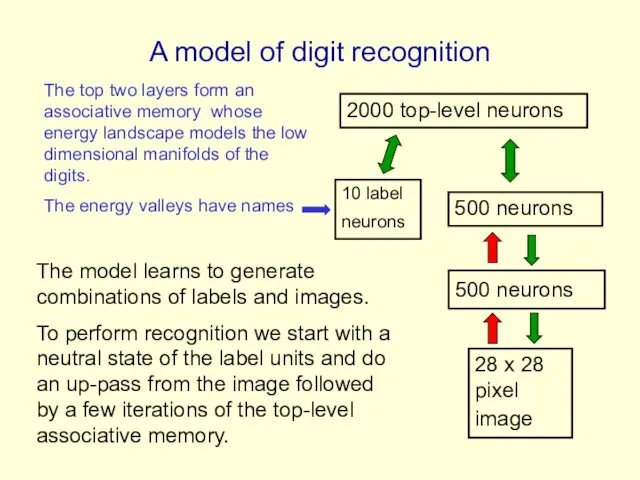
- 33. A model of digit recognition 2000 top-level neurons 500 neurons 500 neurons 28 x 28 pixel
- 34. Fine-tuning with a contrastive version of the “wake-sleep” algorithm After learning many layers of features, we
- 35. Show the movie of the network generating digits (available at www.cs.toronto/~hinton)
- 36. Samples generated by letting the associative memory run with one label clamped. There are 1000 iterations
- 37. Examples of correctly recognized handwritten digits that the neural network had never seen before Its very
- 38. How well does it discriminate on MNIST test set with no extra information about geometric distortions?
- 39. Unsupervised “pre-training” also helps for models that have more data and better priors Ranzato et. al.
- 40. Another view of why layer-by-layer learning works There is an unexpected equivalence between RBM’s and directed
- 41. An infinite sigmoid belief net that is equivalent to an RBM The distribution generated by this
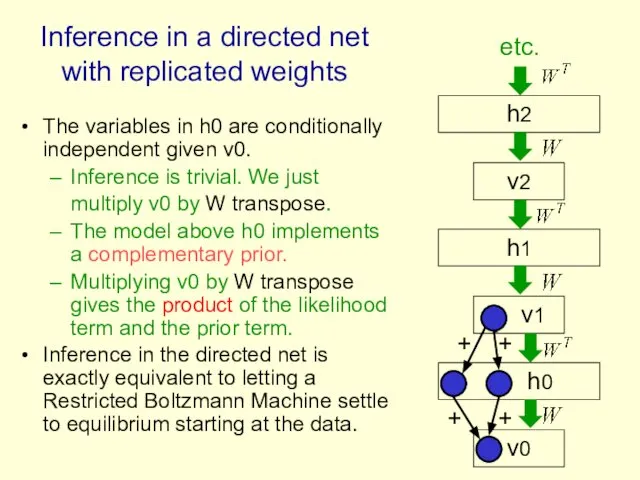
- 42. The variables in h0 are conditionally independent given v0. Inference is trivial. We just multiply v0
- 43. The learning rule for a sigmoid belief net is: With replicated weights this becomes: v1 h1
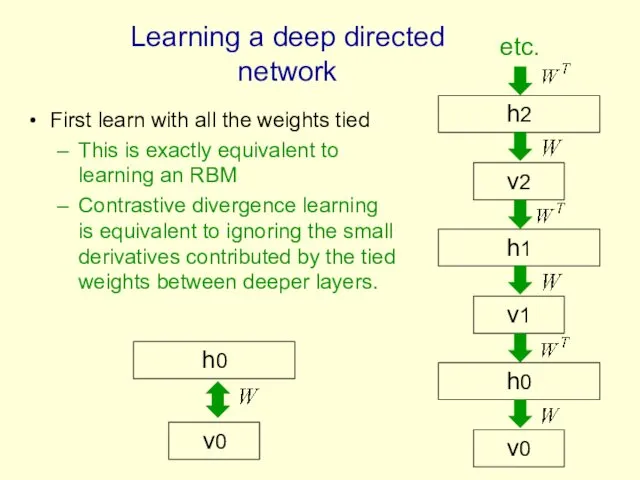
- 44. First learn with all the weights tied This is exactly equivalent to learning an RBM Contrastive
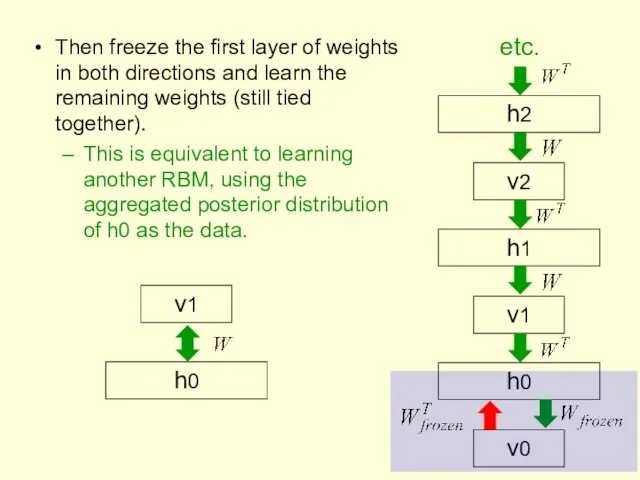
- 45. Then freeze the first layer of weights in both directions and learn the remaining weights (still
- 46. How many layers should we use and how wide should they be? (I am indebted to
- 47. What happens when the weights in higher layers become different from the weights in the first
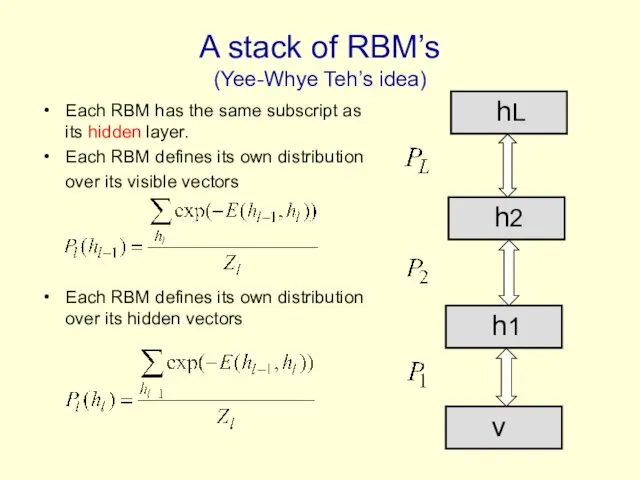
- 48. A stack of RBM’s (Yee-Whye Teh’s idea) Each RBM has the same subscript as its hidden
- 49. The variational bound Now we cancel out all of the partition functions except the top one
- 50. Summary so far Restricted Boltzmann Machines provide a simple way to learn a layer of features
- 51. Overview of the rest of the tutorial How to fine-tune a greedily trained generative model to
- 52. BREAK
- 53. Fine-tuning for discrimination First learn one layer at a time greedily. Then treat this as “pre-training”
- 54. Why backpropagation works better after greedy pre-training Greedily learning one layer at a time scales well
- 55. First, model the distribution of digit images 2000 units 500 units 500 units 28 x 28
- 56. Results on permutation-invariant MNIST task Very carefully trained backprop net with 1.6% one or two hidden
- 57. Combining deep belief nets with Gaussian processes Deep belief nets can benefit a lot from unlabeled
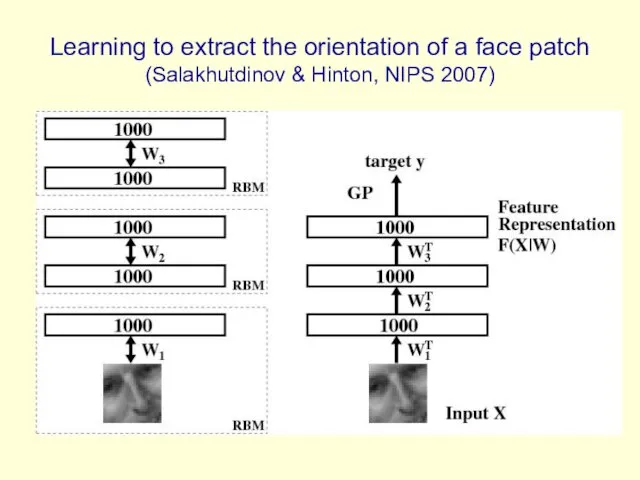
- 58. Learning to extract the orientation of a face patch (Salakhutdinov & Hinton, NIPS 2007)
- 59. The training and test sets 11,000 unlabeled cases 100, 500, or 1000 labeled cases face patches
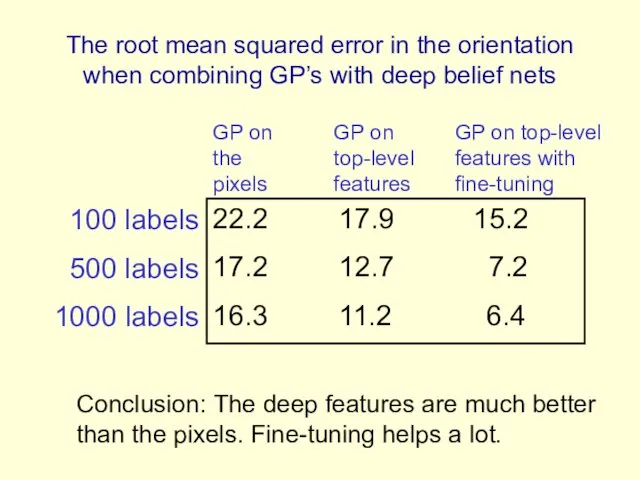
- 60. The root mean squared error in the orientation when combining GP’s with deep belief nets 22.2
- 61. Modeling real-valued data For images of digits it is possible to represent intermediate intensities as if
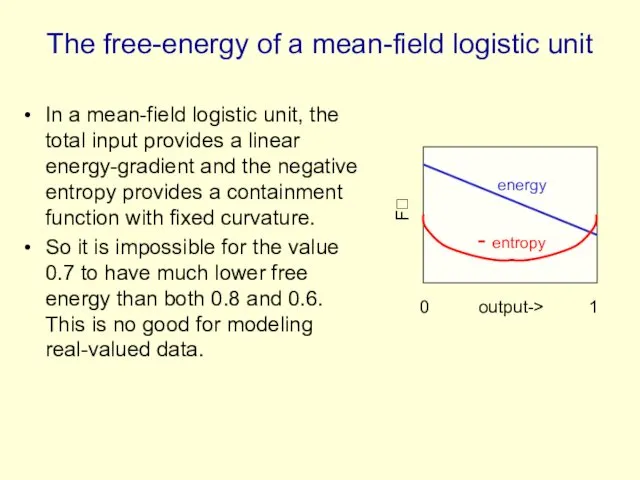
- 62. The free-energy of a mean-field logistic unit In a mean-field logistic unit, the total input provides
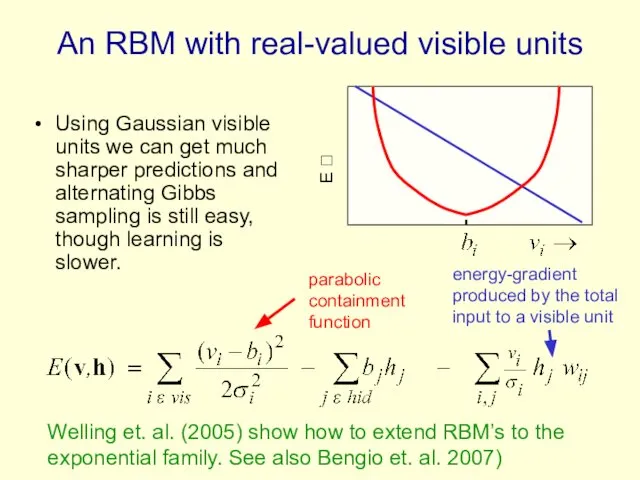
- 63. An RBM with real-valued visible units Using Gaussian visible units we can get much sharper predictions
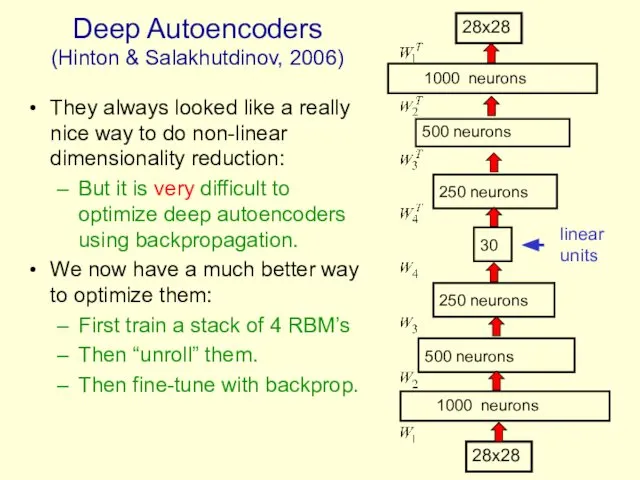
- 64. Deep Autoencoders (Hinton & Salakhutdinov, 2006) They always looked like a really nice way to do
- 65. A comparison of methods for compressing digit images to 30 real numbers. real data 30-D deep
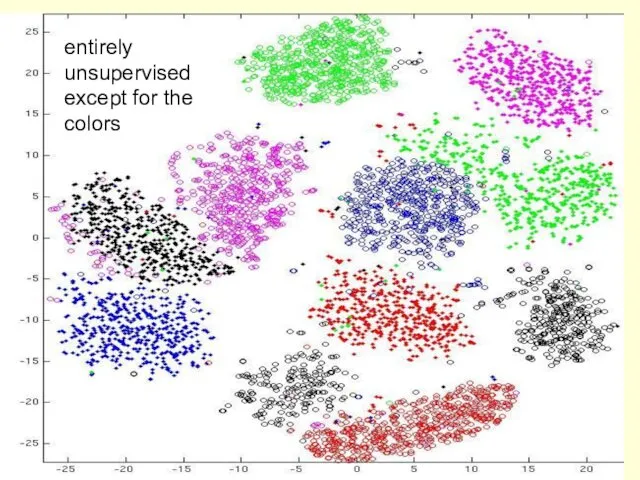
- 66. Do the 30-D codes found by the deep autoencoder preserve the class structure of the data?
- 67. entirely unsupervised except for the colors
- 68. Retrieving documents that are similar to a query document We can use an autoencoder to find
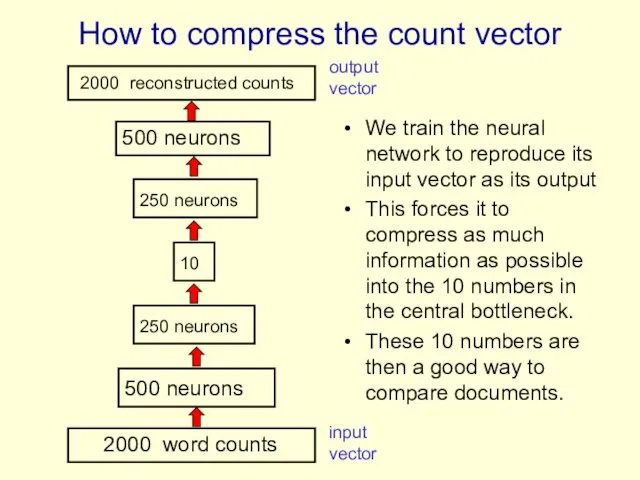
- 69. How to compress the count vector We train the neural network to reproduce its input vector
- 70. Performance of the autoencoder at document retrieval Train on bags of 2000 words for 400,000 training
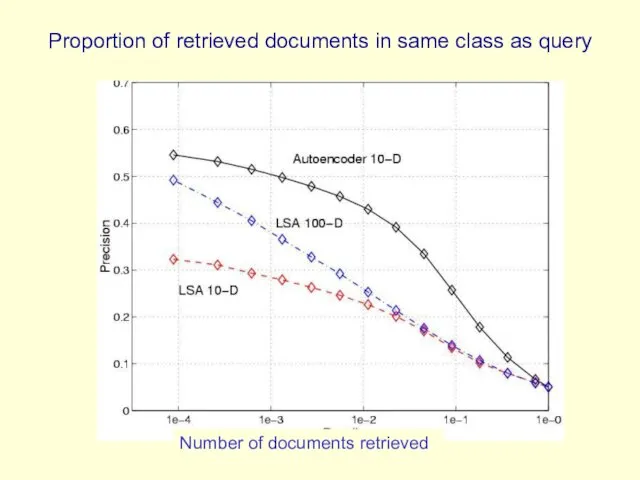
- 71. Proportion of retrieved documents in same class as query Number of documents retrieved
- 72. First compress all documents to 2 numbers using a type of PCA Then use different colors
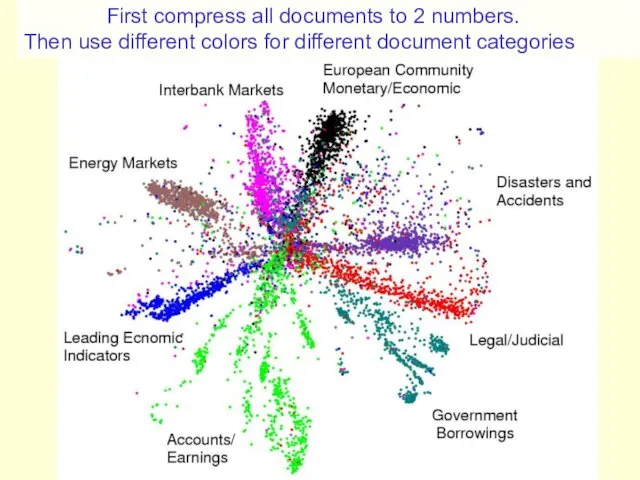
- 73. First compress all documents to 2 numbers. Then use different colors for different document categories
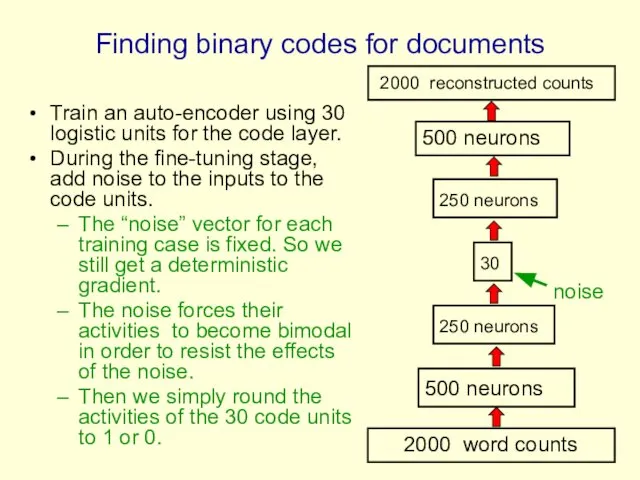
- 74. Finding binary codes for documents Train an auto-encoder using 30 logistic units for the code layer.
- 75. Semantic hashing: Using a deep autoencoder as a hash-function for finding approximate matches (Salakhutdinov & Hinton,
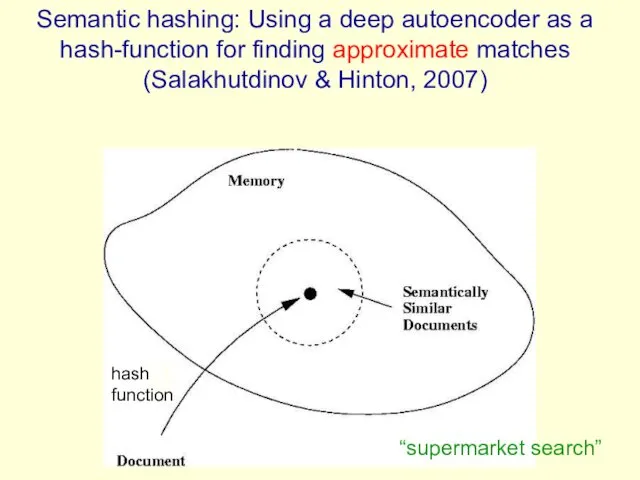
- 76. How good is a shortlist found this way? We have only implemented it for a million
- 77. Time series models Inference is difficult in directed models of time series if we use non-linear
- 78. Time series models If we really need distributed representations (which we nearly always do), we can
- 79. The conditional RBM model (Sutskever & Hinton 2007) Given the data and the previous hidden state,
- 80. Why the autoregressive connections do not cause problems The autoregressive connections do not mess up contrastive
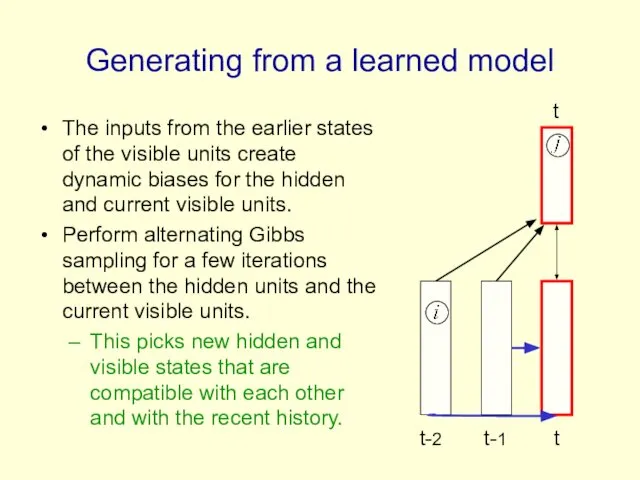
- 81. Generating from a learned model The inputs from the earlier states of the visible units create
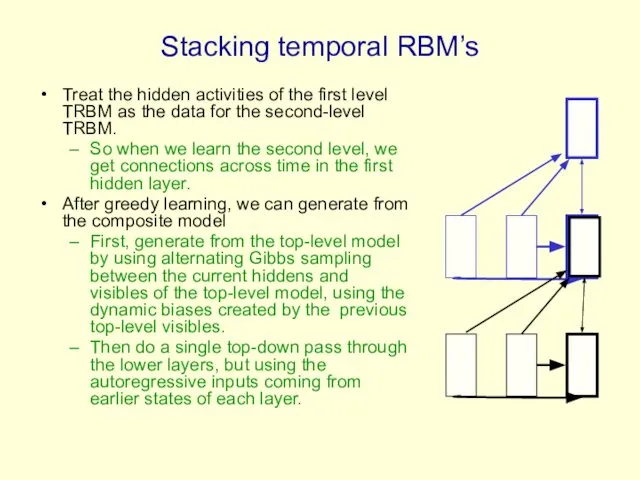
- 82. Stacking temporal RBM’s Treat the hidden activities of the first level TRBM as the data for
- 83. An application to modeling motion capture data (Taylor, Roweis & Hinton, 2007) Human motion can be
- 84. Modeling multiple types of motion We can easily learn to model walking and running in a
- 85. Show Graham Taylor’s movies available at www.cs.toronto/~hinton
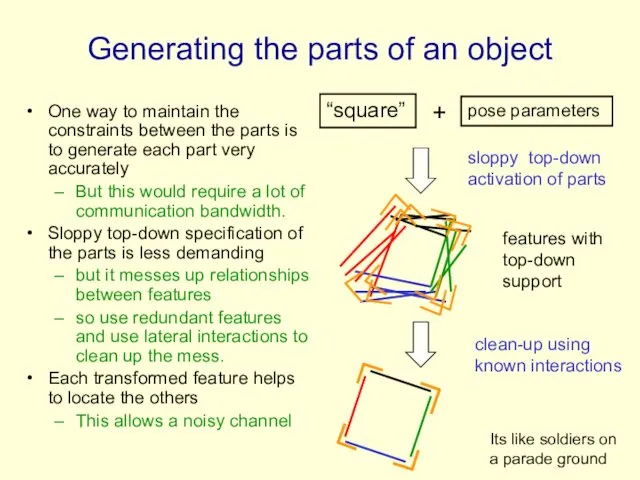
- 86. Generating the parts of an object One way to maintain the constraints between the parts is
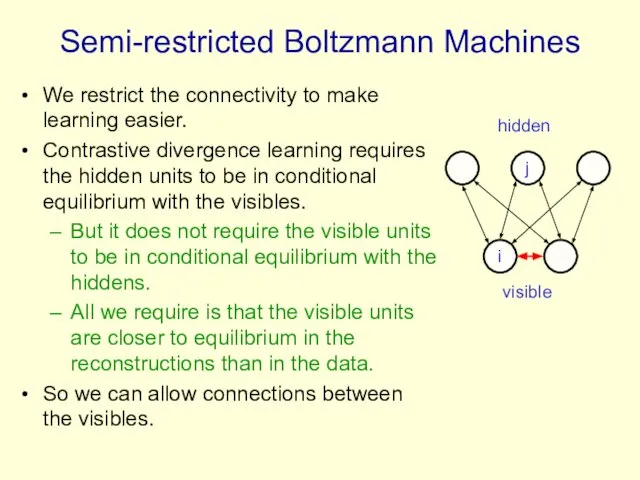
- 87. Semi-restricted Boltzmann Machines We restrict the connectivity to make learning easier. Contrastive divergence learning requires the
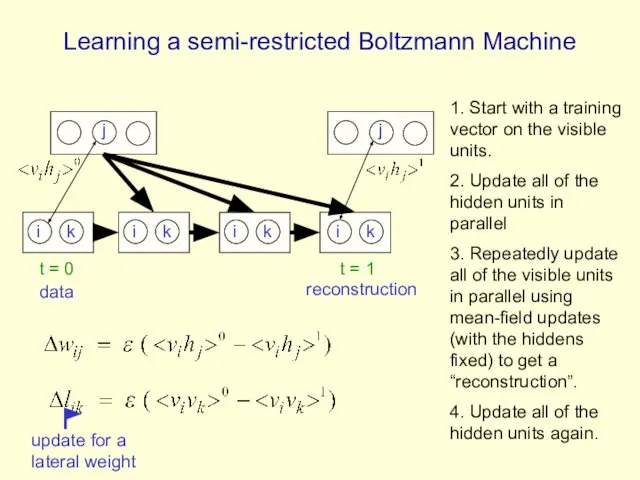
- 88. Learning a semi-restricted Boltzmann Machine i j i j t = 0 t = 1 1.
- 89. Learning in Semi-restricted Boltzmann Machines Method 1: To form a reconstruction, cycle through the visible units
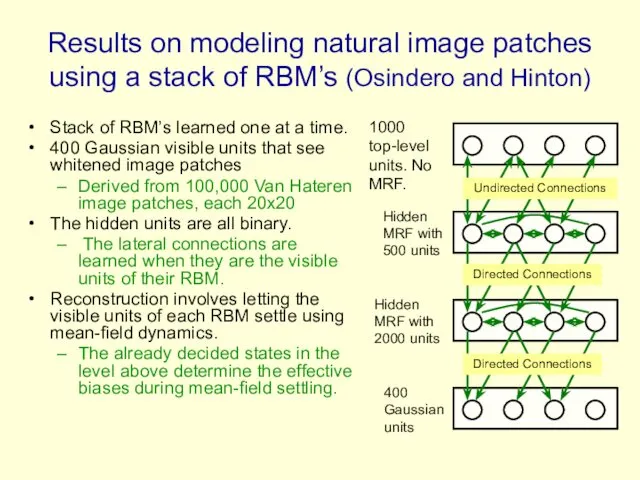
- 90. Results on modeling natural image patches using a stack of RBM’s (Osindero and Hinton) Stack of
- 91. Without lateral connections real data samples from model
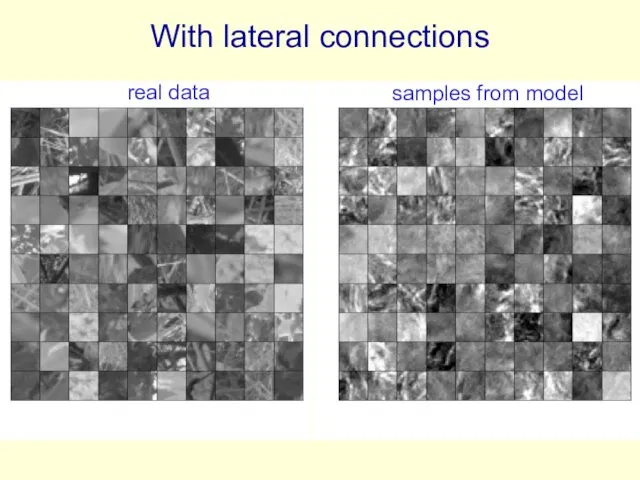
- 92. With lateral connections real data samples from model
- 93. A funny way to use an MRF The lateral connections form an MRF. The MRF is
- 94. Why do we whiten data? Images typically have strong pair-wise correlations. Learning higher order statistics is
- 95. Whitening the learning signal instead of the data Contrastive divergence learning can remove the effects of
- 96. Towards a more powerful, multi-linear stackable learning module So far, the states of the units in
- 97. Higher order Boltzmann machines (Sejnowski, ~1986) The usual energy function is quadratic in the states: But
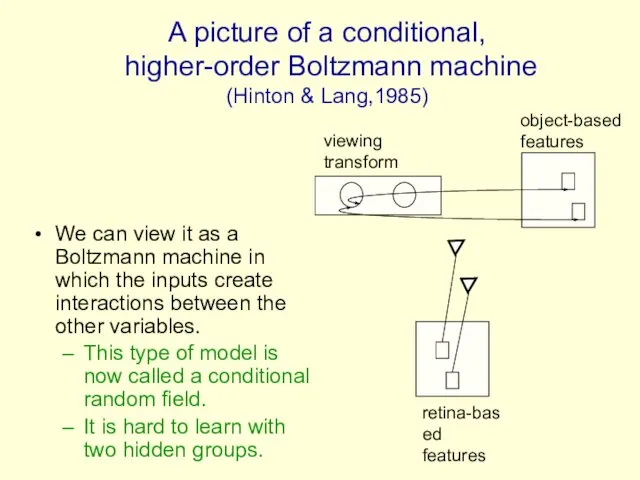
- 98. A picture of a conditional, higher-order Boltzmann machine (Hinton & Lang,1985) retina-based features object-based features viewing
- 99. Using conditional higher-order Boltzmann machines to model image transformations (Memisevic and Hinton, 2007) A transformation unit
- 101. Скачать презентацию































































 Вспомогательный алгоритм
Вспомогательный алгоритм Язык разметки гипертекста HTML (Hyper Text Markup Language )
Язык разметки гипертекста HTML (Hyper Text Markup Language ) Использование подзапросов для решения запросов
Использование подзапросов для решения запросов Презентация на тему МОДЕЛИРОВАНИЕ И ФОРМАЛИЗАЦИЯ
Презентация на тему МОДЕЛИРОВАНИЕ И ФОРМАЛИЗАЦИЯ Визуализация параметрических исследований
Визуализация параметрических исследований Смартфон в житті. Застосування в життєвих ситуаціях
Смартфон в житті. Застосування в життєвих ситуаціях Модели данных в информационных системах
Модели данных в информационных системах Файлы и папки
Файлы и папки  Правовая информатика
Правовая информатика Компьютерное конструирование. Исходные данные для проектирования модели упорного подшипника скольжения в Компас-3D
Компьютерное конструирование. Исходные данные для проектирования модели упорного подшипника скольжения в Компас-3D Программалық жабдыққа қатысты талаптармен жұмыс істеу принциптері. Жобалау мәселелері
Программалық жабдыққа қатысты талаптармен жұмыс істеу принциптері. Жобалау мәселелері Администрирование информационных систем Шифрование
Администрирование информационных систем Шифрование  Create a own Database
Create a own Database Виртуальный обзор ПК, на который установлено ПО
Виртуальный обзор ПК, на который установлено ПО Файлы и файловая система
Файлы и файловая система Презентация по информатике Элементы статистической обработки данных 7 класс
Презентация по информатике Элементы статистической обработки данных 7 класс Представление чисел в памяти компьютера. 10 класс
Представление чисел в памяти компьютера. 10 класс Презентация "MSC.Mvision Appendix C" - скачать презентации по Информатике
Презентация "MSC.Mvision Appendix C" - скачать презентации по Информатике Выполнение запросов, создание и редактирование отчета. MS Access
Выполнение запросов, создание и редактирование отчета. MS Access Графические приемы. Лекция 2
Графические приемы. Лекция 2 Тенологія створення кишенькового календаря
Тенологія створення кишенькового календаря Курс «С#. Программирование на языке высокого уровня» Павловская Т.А.
Курс «С#. Программирование на языке высокого уровня» Павловская Т.А.  Твоя безопасная сеть
Твоя безопасная сеть Объектно-ориентированные подходы
Объектно-ориентированные подходы Классификация устройств хранения данных
Классификация устройств хранения данных Net pay`. Агрегатор электронных платежей
Net pay`. Агрегатор электронных платежей Министерство образования и науки Республики Башкортостан Государственное бюджетное
Министерство образования и науки Республики Башкортостан Государственное бюджетное Таблицы HTML - документов
Таблицы HTML - документов