Содержание
- 7. Числа Фибоначчи Решение методом «динамического программирования» предполагает запоминание каждого числа в массиве. Тогда N-е число Фибоначчи
- 8. Задача об n – битных двоичных числах Найти количество F всех n – битных двоичных чисел,
- 9. F[N] = F[N-1] + F[N-2], при N > 2. Задача об n – битных двоичных числах
- 10. Зайчик на лесенке На вершине лесенки, содержащей N ступенек, находится зайчик, который начинает прыгать по ним
- 11. Зайчик на лесенке Пусть зайчик находится на ступеньке с номером X. По условию он может спрыгнуть
- 12. Программа на С++ #include using namespace std; int main() { int N; long long F[31]; cin>>N;
- 13. Задача о фишке Фишка может двигаться по полю длины N только вперед. Длина хода фишки не
- 14. Задача о фишке Пусть S[i] - количество различных путей, по которым фишка может пройти поле от
- 15. Алгоритм динамического программирования Динамическое программирование – метод оптимизации, приспособленный к задачам, в которых требуется построить решение
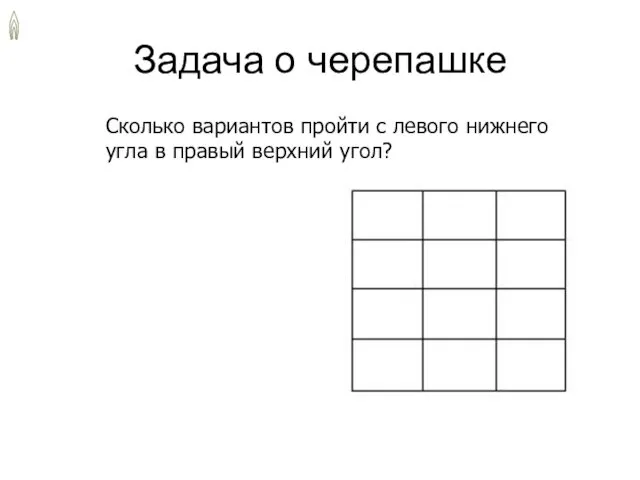
- 16. Задача о черепашке Сколько вариантов пройти с левого нижнего угла в правый верхний угол?
- 17. Формулировка задачи динамического программирования Дано: множество состояний в том числе начальное и конечное множество возможных переходов
- 18. Пример 0 18 1 2 3 5 7 6 8 10 12 11 13 4 14
- 19. Математическая запись /9
- 20. Принцип оптимальности Беллмана Если вершины A и B лежат на оптимальном пути между вершинами 0 и
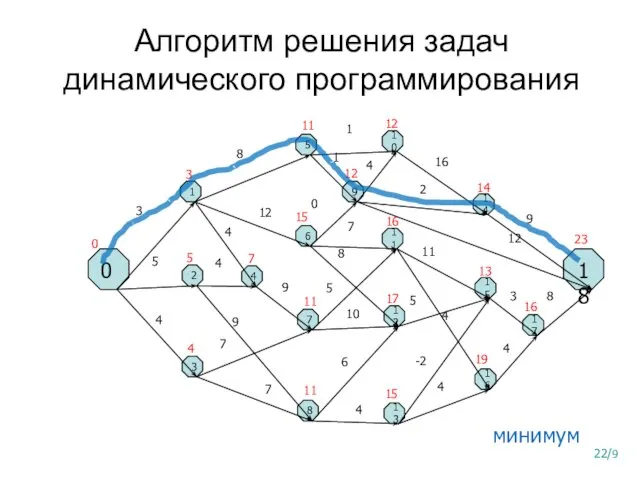
- 21. Алгоритм решения задач динамического программирования 0 18 1 2 3 5 7 6 8 10 12
- 22. Алгоритм решения задач динамического программирования 0 18 1 2 3 5 7 6 8 10 12
- 23. Экономические приложения /9
- 25. Скачать презентацию







![F[N] = F[N-1] + F[N-2], при N > 2. Задача об n – битных двоичных числах](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/450988/slide-8.jpg)




![Задача о фишке Пусть S[i] - количество различных путей, по которым](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/450988/slide-13.jpg)







 Алгоритм. Алгоритм для робота
Алгоритм. Алгоритм для робота Створення банку ідей. (10 клас)
Створення банку ідей. (10 клас) Программируемые контроллеры Siemens - часть 1. Основные понятия и терминология
Программируемые контроллеры Siemens - часть 1. Основные понятия и терминология Введение в Базы данных
Введение в Базы данных Психопрофилактическая компьютерная программа «Волна» Презентацию подготовила педагог – психолог МБОУ СОШ №3 г.Нарьян – Мар Дурк
Психопрофилактическая компьютерная программа «Волна» Презентацию подготовила педагог – психолог МБОУ СОШ №3 г.Нарьян – Мар Дурк Программа по обработке файла в оконном режиме
Программа по обработке файла в оконном режиме Решение задач на компьютере алгоритмизация и программирование
Решение задач на компьютере алгоритмизация и программирование Л.В. Кокышевтинг чумдемелдери эмодзи jуруктарда
Л.В. Кокышевтинг чумдемелдери эмодзи jуруктарда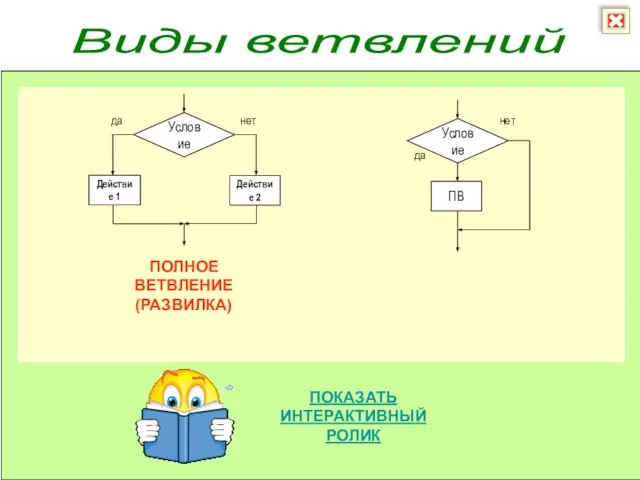 Виды ветвлений
Виды ветвлений Средства пакета Microsoft Office. PowerPoint
Средства пакета Microsoft Office. PowerPoint Разработка компьютерного сурдопереводчика непрерывной русской речи на разговорный русский жестовый язык для глухих
Разработка компьютерного сурдопереводчика непрерывной русской речи на разговорный русский жестовый язык для глухих Использование ЭОР в начальных классах как средство повышения качества образования
Использование ЭОР в начальных классах как средство повышения качества образования Макросы
Макросы Этапы решения задач на компьютере
Этапы решения задач на компьютере Введение в Python
Введение в Python Администрирование информационных систем Администрирование БД. Управление разрешениями
Администрирование информационных систем Администрирование БД. Управление разрешениями  Системы счисления
Системы счисления Безопасный Интернет
Безопасный Интернет Системное программирование
Системное программирование Введение в базы данных
Введение в базы данных ОСНОВЫ ЛОГИКИ Кривенцов Л.А.
ОСНОВЫ ЛОГИКИ Кривенцов Л.А. Система оптического распознавания текстов
Система оптического распознавания текстов Використання ментальних карт на уроках інформатики
Використання ментальних карт на уроках інформатики Лекция 1. Компьютерная графика. Карты
Лекция 1. Компьютерная графика. Карты Оперативной Картографии
Оперативной Картографии Предистория информатики
Предистория информатики Презентация "Графический редактор Adobe Photoshop" - скачать презентации по Информатике
Презентация "Графический редактор Adobe Photoshop" - скачать презентации по Информатике Distributed systems.Computing
Distributed systems.Computing