Содержание
- 2. 1 2 3 4 5 2 2 1 1 1 3 3 4 w(T)=7 ФПМИ БГУ
- 3. Число остовных деревьев полного графа Теорема Кэли о числе деревьев (1889 г.) На n вершинах, пронумерованных
- 4. Построение кода Прюфера Пока вершин более 2-х: Выбрать лист v с минимальным номером (лист - вершина
- 5. Восстановление дерева по коду Прюфера Код: {1, 4, 5, 5} Вершины: V= {1, 2, 3, 4,
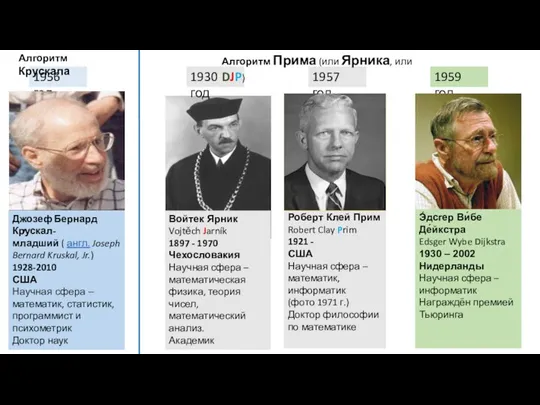
- 6. 1956 год 1957 год 1959 год Э́дсгер Ви́бе Де́йкстра Edsger Wybe Dijkstra 1930 – 2002 Нидерланды
- 7. Алгоритм Крускала (1956 г.) Джозеф Бернард Крускал-младший ( англ. Joseph Bernard Kruskal, Jr.) 1928-2010 США Научная
- 8. Алгоритм Крускала Упорядочим все рёбра E графа G по неубыванию веса. Минимальное остовное дерево графа G
- 9. Для просмотра рёбер по неубыванию веса можно использовать следующие структуры данных: массив добавить в массив все
- 10. Для определения наличия цикла с ранее выбранными в остов рёбрами можно использовать структуру данных система непересекающихся
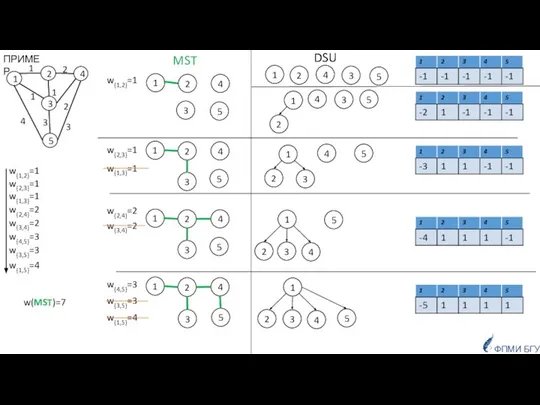
- 11. ФПМИ БГУ w{2,3}=1 w{1,2}=1 w{2,4}=2 w{1,3}=1 w{3,5}=3 w{3,4}=2 w{4,5}=3 w{1,5}=4 1 2 3 4 5 1
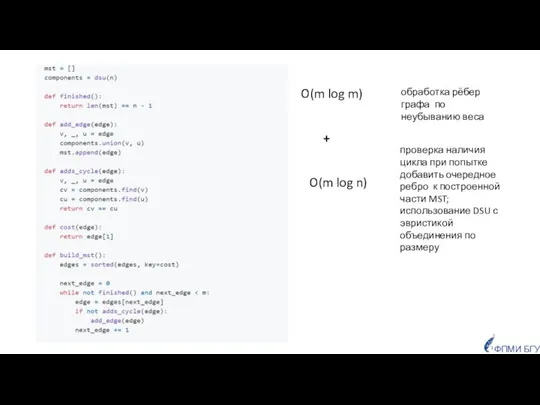
- 12. O(m log n) обработка рёбер графа по неубыванию веса проверка наличия цикла при попытке добавить очередное
- 13. Обоснование корректности алгоритма Крускала ФПМИ БГУ
- 14. Алгоритм Прима (или Ярника, или DJP) 1957 год 1959 год Э́дсгер Ви́бе Де́йкстра Edsger Wybe Dijkstra
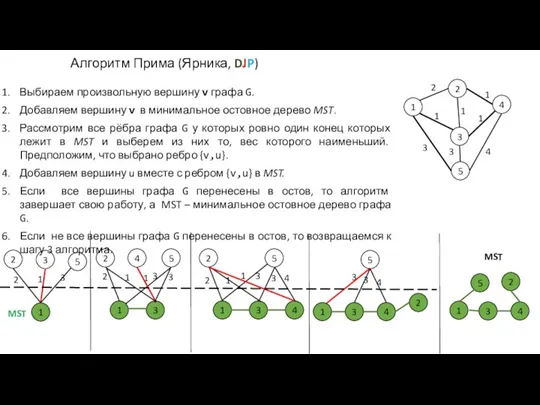
- 15. Алгоритм Прима (Ярника, DJP) Выбираем произвольную вершину v графа G. Добавляем вершину v в минимальное остовное
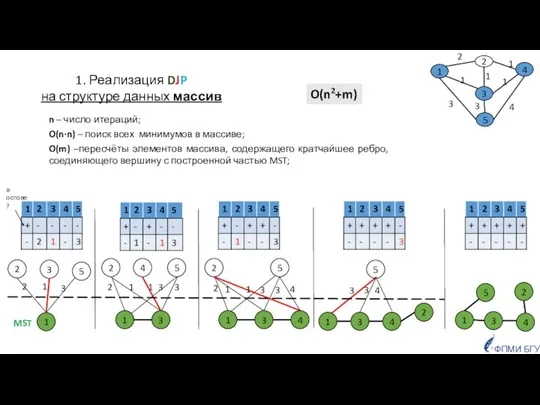
- 16. n – число итераций; O(n∙n) – поиск всех минимумов в массиве; O(m) –пересчёты элементов массива, содержащего
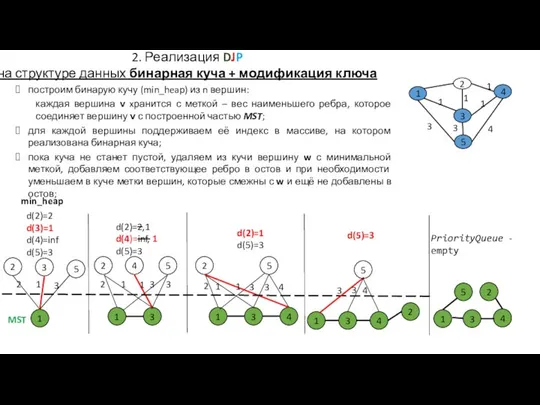
- 17. построим бинарую кучу (min_heap) из n вершин: каждая вершина v xранится с меткой – вес наименьшего
- 18. создание кучи из n вершин (в куче каждая вершина v xранится с меткой – вес наименьшего
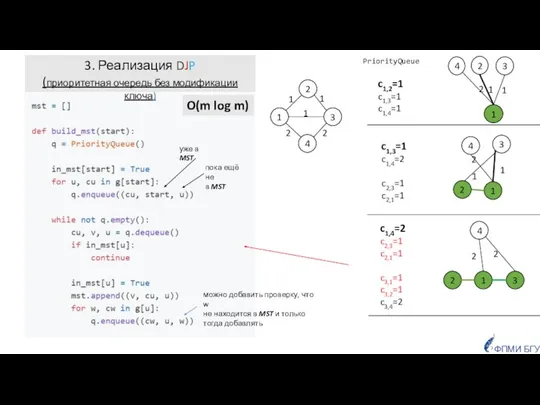
- 19. O(m log m) 1 2 4 3 1 1 1 2 2 1 3 2 1
- 20. ФПМИ БГУ
- 21. Жадный алгоритм оптимально решает задачу о минимальном остовном дереве. Какие задачи можно решить оптимально жадным алгоритмом?
- 22. Матроиды
- 25. Некоторые комбинаторные задачи для систем подмножеств могут быть решены корректно (точно) «жадным» алгоритмом, а некоторые нет
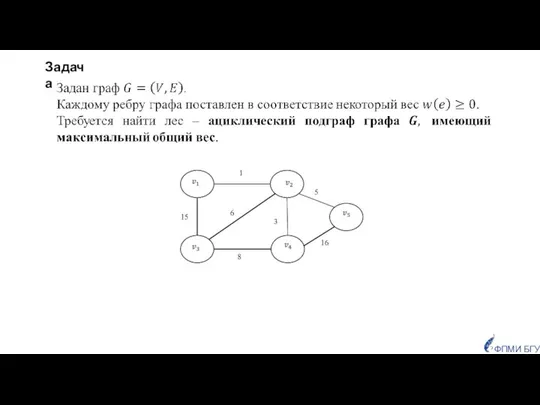
- 27. ФПМИ БГУ Задача
- 28. ФПМИ БГУ Решение
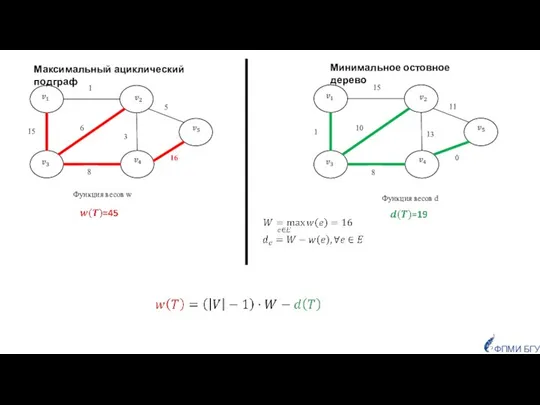
- 29. ФПМИ БГУ de=W-we, ∀e∈E, где W=maxe∈Ewe=15. Функция весов w Минимальное остовное дерево Максимальный ациклический подграф
- 30. Рассмотренная в задаче система подмножеств является матроидом, который называют графическим. «Жадный» алгоритм корректно решает задачу о
- 31. Задача о лесе максимального веса по существу, может рассматриваться как задача о минимальном остовном дереве, но
- 33. Скачать презентацию




















 Национальная безопасность РФ в информационной сфере
Национальная безопасность РФ в информационной сфере Круговые диаграммы
Круговые диаграммы Файловая система. Определения
Файловая система. Определения Программное обеспечение Docker
Программное обеспечение Docker Источники ошибок в ПК Прусак А.В.
Источники ошибок в ПК Прусак А.В.  Комплекс упражнений для глаз Бородина Т. А., учитель информатики ОУ СОШ №3 «ОЦ» г. Сызрани
Комплекс упражнений для глаз Бородина Т. А., учитель информатики ОУ СОШ №3 «ОЦ» г. Сызрани Язык запросов к реляционным базам данных
Язык запросов к реляционным базам данных Пример проведения Прогон-1
Пример проведения Прогон-1 Стандарты BIM. Форматы обмена данными
Стандарты BIM. Форматы обмена данными Процессор
Процессор Антивирусная защита
Антивирусная защита Разработка модуля формирования листа согласования электронных документов в IPS
Разработка модуля формирования листа согласования электронных документов в IPS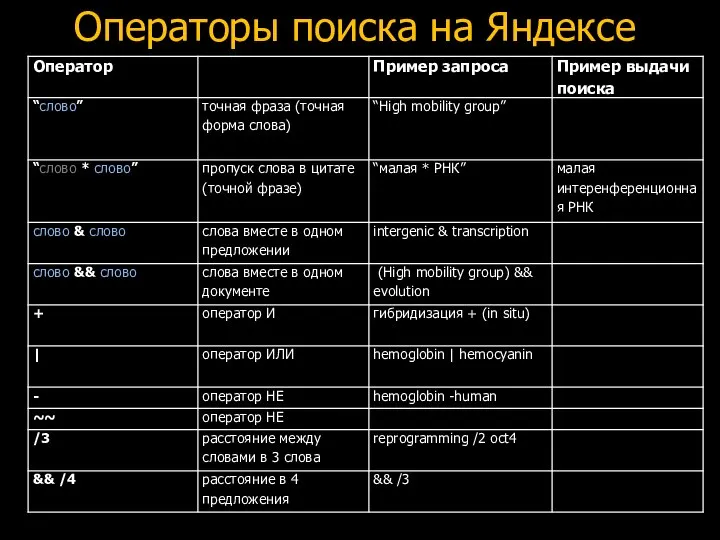 Операторы поиска на Яндексе
Операторы поиска на Яндексе Методы. Что такое метод?
Методы. Что такое метод? Компьютерная память. 8 класс
Компьютерная память. 8 класс Реестр сведений об организациях отдыха детей и их оздоровления в ульяновской области
Реестр сведений об организациях отдыха детей и их оздоровления в ульяновской области Аппаратные и программные средства компьютерной сети
Аппаратные и программные средства компьютерной сети Computer Software Engineering
Computer Software Engineering Основы логики
Основы логики Отличия группы ВК от публичной страницы
Отличия группы ВК от публичной страницы Устройства компьютера
Устройства компьютера Алгоритмы и кейсы
Алгоритмы и кейсы Информация. Кодирование. Измерение
Информация. Кодирование. Измерение Модели и моделирование. Математическое моделирование
Модели и моделирование. Математическое моделирование Аттестационная работа. Образовательная программа курса внеурочной деятельности для 4-х классов Юный информатик
Аттестационная работа. Образовательная программа курса внеурочной деятельности для 4-х классов Юный информатик Алгоритмическая конструкция ветвление
Алгоритмическая конструкция ветвление Алгоритм ветвления и циклические алгоритмы. 9 класс
Алгоритм ветвления и циклические алгоритмы. 9 класс IT-технологии
IT-технологии