Содержание
- 2. Задание. Построить комбинационные схемы в различных базисах, реализующие не полностью определенную булеву функцию f(Х) = f
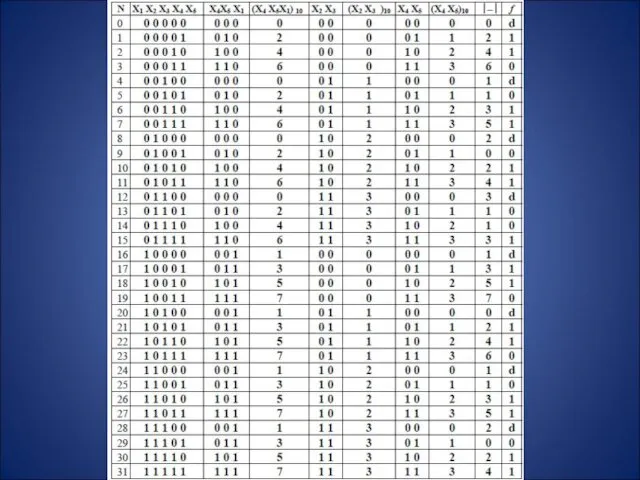
- 4. Представление булевой функции в аналитическом виде
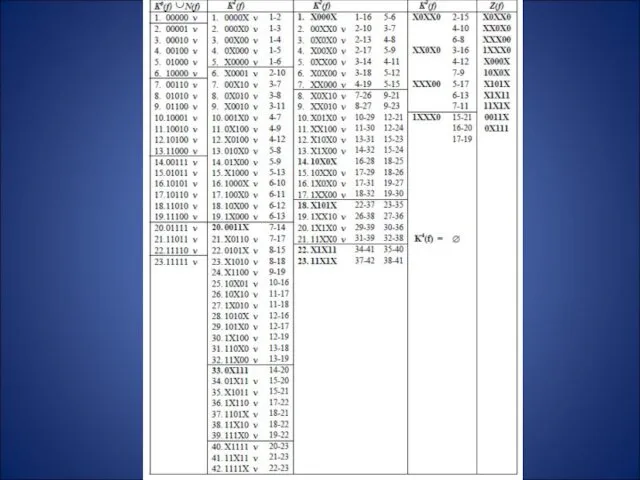
- 5. Минимизация булевой функции методом Квайна –Мак-Класки Нахождение простых импликант (максимальных кубов).
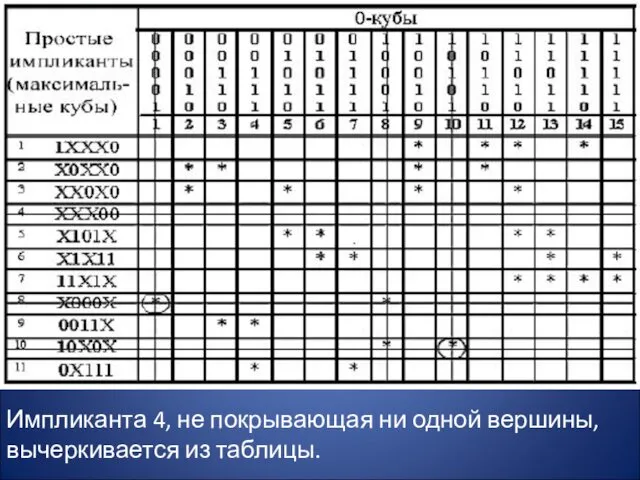
- 7. Составление импликантной таблицы. Импликантная таблица содержит 11 строк (по числу простых импликант) и 15 столбцов (по
- 8. Импликанта 4, не покрывающая ни одной вершины, вычеркивается из таблицы.
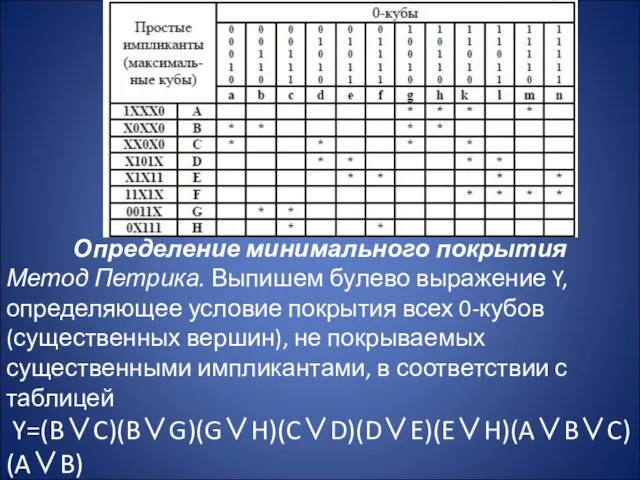
- 9. Определение существенных импликант. Импликанты 8 и 10 – существенные, так как они покрывают вершины 1 и
- 10. Определение минимального покрытия Метод Петрика. Выпишем булево выражение Y, определяющее условие покрытия всех 0-кубов (существенных вершин),
- 11. Применим закон поглощения к дизъюнктивным термам, в результате чего в выражении остаются только двухбуквенные термы Y=(B∨C)(B∨G)(G∨H)(C∨D)(D∨E)(E∨H)(A∨B)(A∨F)(E∨F)
- 12. Возможны следующие варианты покрытия:
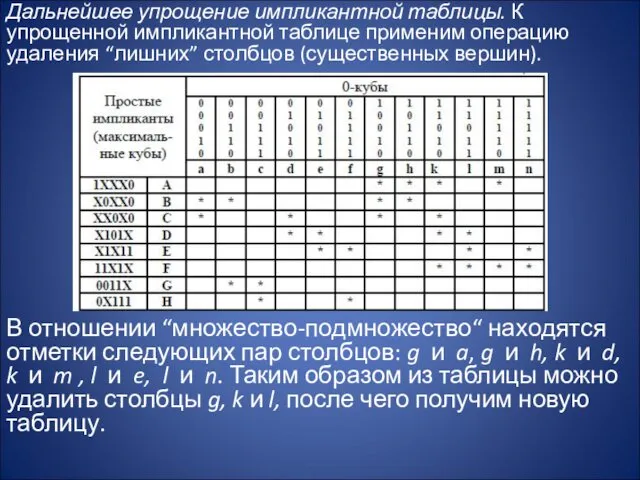
- 14. Дальнейшее упрощение импликантной таблицы. К упрощенной импликантной таблице применим операцию удаления “лишних” столбцов (существенных вершин). В
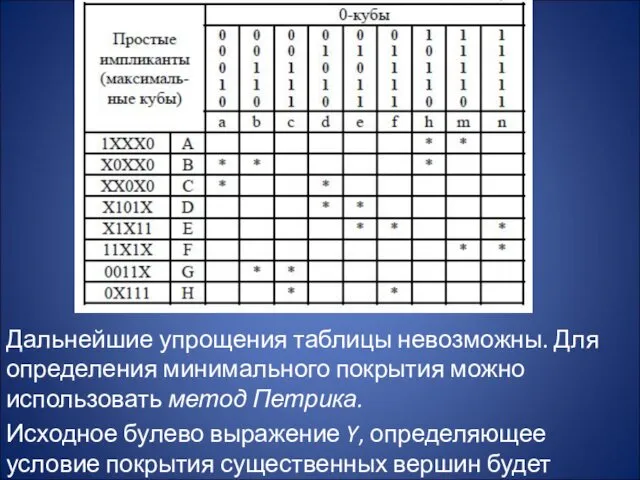
- 15. Дальнейшие упрощения таблицы невозможны. Для определения минимального покрытия можно использовать метод Петрика. Исходное булево выражение Y,
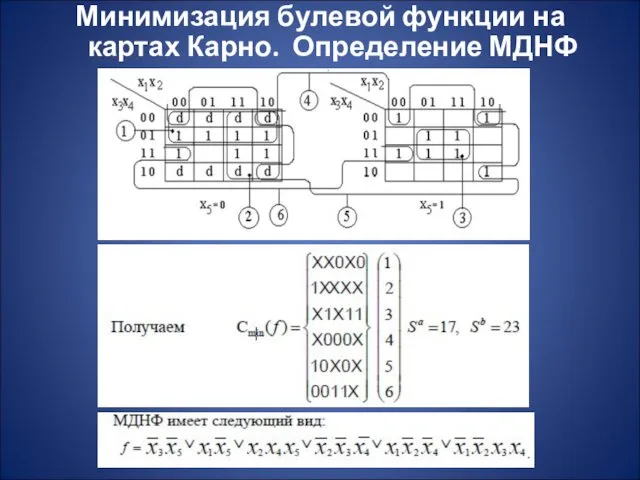
- 16. Минимизация булевой функции на картах Карно. Определение МДНФ
- 17. Определение МКНФ ,,,
- 18. Преобразование минимальных форм булевой функции Факторное преобразование для МДНФ: (SQ=23) (SQ=20) (SQ=18) Решим задачу декомпозиции применительно
- 19. Реализация комбинационной схемы по этому выражению с учетом затрат на вспомогательную функцию ϕ и ее инверсию
- 20. Следует отметить, что вынесение x4 из первых двух термов МКНФ не дает уменьшения цены схемы: ΔSQ
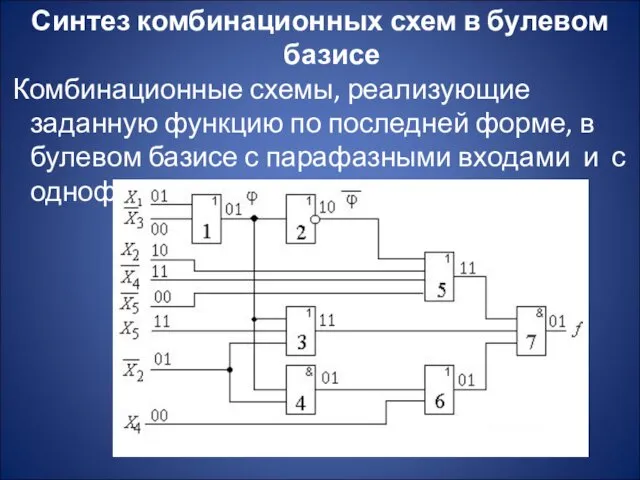
- 21. Синтез комбинационных схем в булевом базисе Комбинационные схемы, реализующие заданную функцию по последней форме, в булевом
- 22. Задержка схемы с парафазными входами Т=4τ, цена схемы SQ=17. Для схемы с однофазными входами Т=5τ, цена
- 23. Синтез комбинационных схем в универсальных базисах Базис ИЛИ-НЕ а) Приведение последнего выражения к базису ИЛИ-НЕ осуществляется
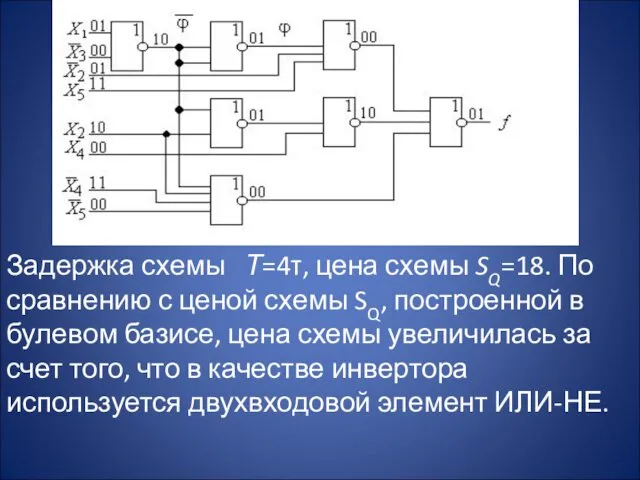
- 24. Задержка схемы Т=4τ, цена схемы SQ=18. По сравнению с ценой схемы SQ, построенной в булевом базисе,
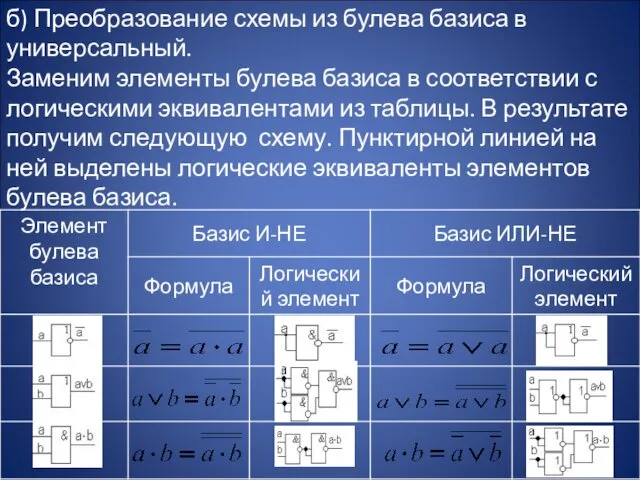
- 25. б) Преобразование схемы из булева базиса в универсальный. Заменим элементы булева базиса в соответствии с логическими
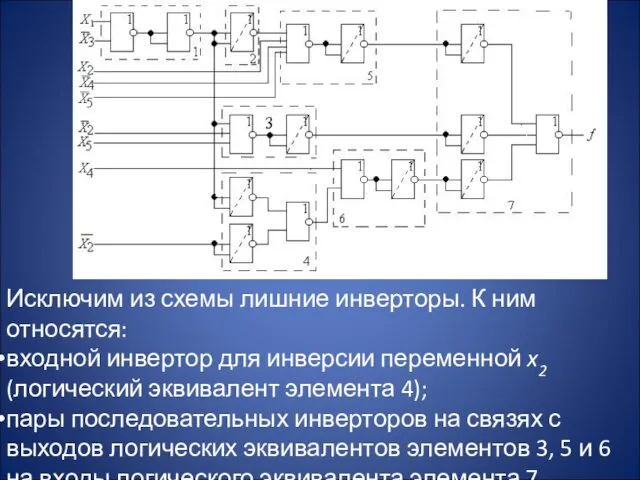
- 26. Исключим из схемы лишние инверторы. К ним относятся: входной инвертор для инверсии переменной x2 (логический эквивалент
- 27. Кроме того, пары последовательных инверторов составляют выходной инвертор логического эквивалента элемента 1, на котором реализуется вспомогательная
- 28. После удаления замыкающих инверторов обеих пар, на выходах которых реализуется инверсия ϕ, входы логических эквивалентов элементов
- 29. булева базиса на операцию штрих Шеффера (отрицание конъюнкции) путем использования законов двойственности. Цена схемы в базисе
- 30. Для построения схемы с меньшей ценой целесообразно использовать форму, полученную по МДНФ с ценой SQ=18 для
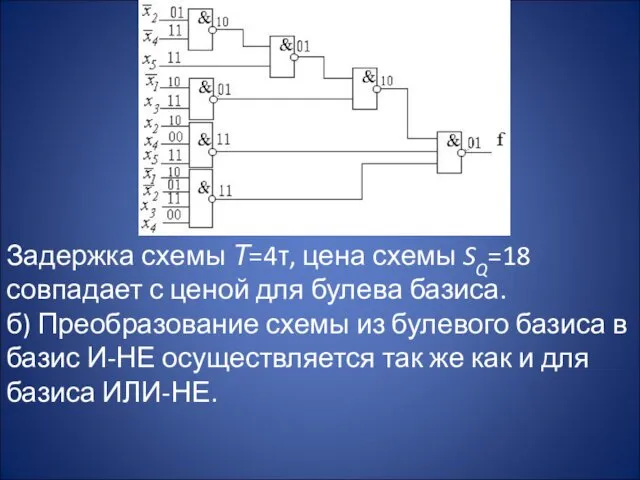
- 31. Задержка схемы Т=4τ, цена схемы SQ=18 совпадает с ценой для булева базиса. б) Преобразование схемы из
- 32. Синтез комбинационной схемы с учетом коэффициента объединения При построении схемы в универсальном базисе с учетом ограничения
- 33. Если в выражении для функции имеются трехмест-ные операции, то при I=2 для уменьшения задерж-ки синтезируемой схемы
- 34. Кроме того, при объединении скобок как элементов трехместной операции конъюнкции уединим среднюю скобку, как более сложный
- 35. Инверсии реализуются в схеме, построенной по этому выражению, на элементах ИЛИ-НЕ с запараллеленными входами.
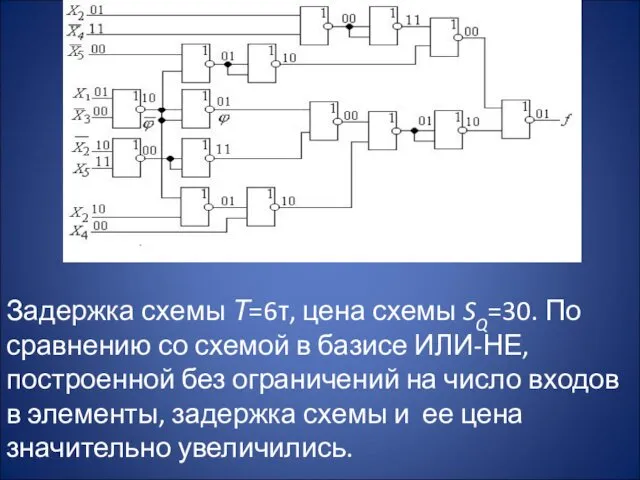
- 36. Задержка схемы Т=6τ, цена схемы SQ=30. По сравнению со схемой в базисе ИЛИ-НЕ, построенной без ограничений
- 37. Замечание. Использование в качестве исходного выражения с последующей дополнительной факторизацией путем вынесения за скобки x4 из
- 38. Анализ комбинационных схем По таблице истинности булевой функции выберем наборы аргументов (входных переменных), на кото-рых функция
- 39. Синтез многовыходных комбинационных схем ПРИМЕР 2. Синтезировать комбинационную схему, выполняющую операцию сложения двух двухразрядных двоичных чисел:
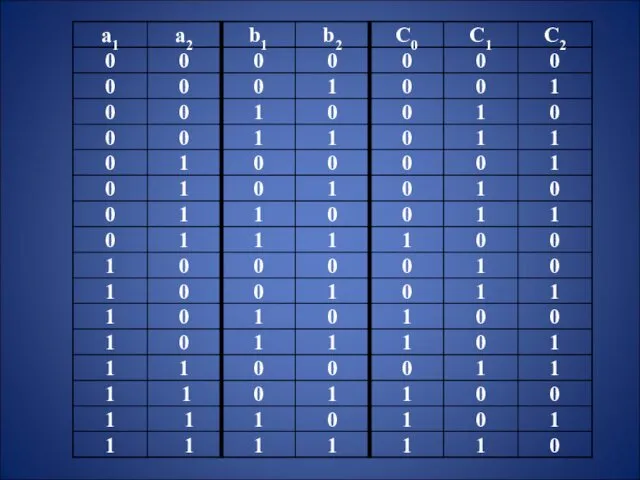
- 40. 1. Составление таблицы истинности Таблица истинности системы булевых функций строится с учетом правил двоичного сложения и
- 51. Скачать презентацию


































 С++. Циклические операторы
С++. Циклические операторы Электронная почта
Электронная почта  Интерфейс Человек-ЭВМ
Интерфейс Человек-ЭВМ Стандартные диалоговые окна
Стандартные диалоговые окна Винни-Пух и пчелы
Винни-Пух и пчелы МОУ «Авсюнинская средняя общеобразовательная школа» Исследовательская работа по русскому языку «Язык СМС – язык будущего?»
МОУ «Авсюнинская средняя общеобразовательная школа» Исследовательская работа по русскому языку «Язык СМС – язык будущего?»  Смешарики. Imperium 8 эпизод Первое противостояние
Смешарики. Imperium 8 эпизод Первое противостояние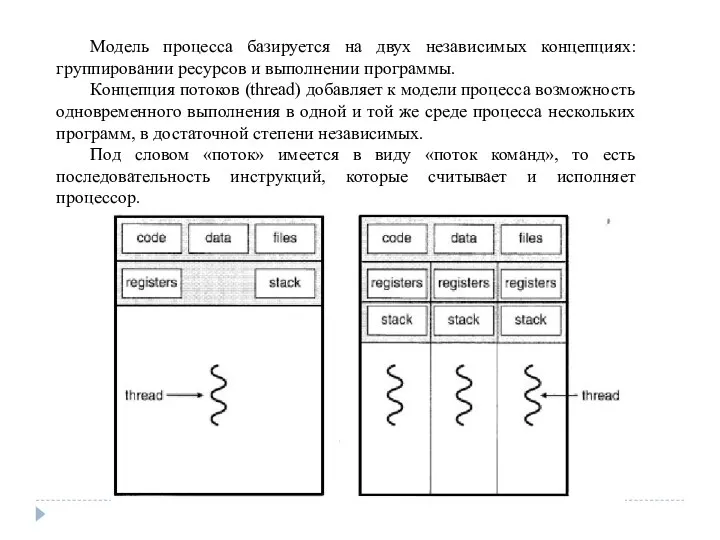 Процессы и потоки
Процессы и потоки Переменные. Память компьютера в наших руках
Переменные. Память компьютера в наших руках Компьютерные презентации Урок информатики 10 класс
Компьютерные презентации Урок информатики 10 класс Мы едины
Мы едины Решение задачи №11 Анализирование информации, представленной в виде схем
Решение задачи №11 Анализирование информации, представленной в виде схем Mobile phone App Installation operation
Mobile phone App Installation operation Объектно-ориентированный подход
Объектно-ориентированный подход Шаблон для создания викторины
Шаблон для создания викторины Электронные ресурсы: правила составления библиографического описания
Электронные ресурсы: правила составления библиографического описания Администрирование в информационных системах Веб-службы и сервисы Администрирование веб-служб
Администрирование в информационных системах Веб-службы и сервисы Администрирование веб-служб  Перегляд документа. Стилі та їх використання (10 клас)
Перегляд документа. Стилі та їх використання (10 клас) Протоколы и службы прикладного уровня
Протоколы и службы прикладного уровня Системы автоматизированного проектирования (САПР)
Системы автоматизированного проектирования (САПР) Презентация "Понятие информации. Информационных процессов" - скачать презентации по Информатике
Презентация "Понятие информации. Информационных процессов" - скачать презентации по Информатике Мобильные блоги
Мобильные блоги Продукционная модель
Продукционная модель Презентация Перевод числе в 2,8,16-ую системы счисления
Презентация Перевод числе в 2,8,16-ую системы счисления Текстовый редактор Microsoft Word
Текстовый редактор Microsoft Word Дискретный анализ Лекция 3 Комбинаторика. Перестановки
Дискретный анализ Лекция 3 Комбинаторика. Перестановки  Арифметические операции в позиционных системах счисления
Арифметические операции в позиционных системах счисления Система диспетчерского контроля и управления
Система диспетчерского контроля и управления