Содержание
- 2. Алгоритм — совокупность действий, необходимых для решения задачи Алгоритмы могут быть записаны на: естественном языке на
- 3. ТИПЫ АЛГОРИТМОВ Детерминированный Недетерминированный Алгоритм моделирования НГТУ, кафедра АСУ, Лауферман О.В.
- 4. Детерминированные алгоритмы Детерминированные алгоритмы всегда обеспечивают регулярные решения. В них отсутствуют элементы, вносящие неопределенность, для них
- 5. Недетерминированные алгоритмы Некоторые из задач являются по природе недетерминированными, и можно показать, что для них не
- 6. Алгоритмы моделирования Третий, основной тип алгоритмов, предназначен не для поиска ответа на поставленную задачу, а для
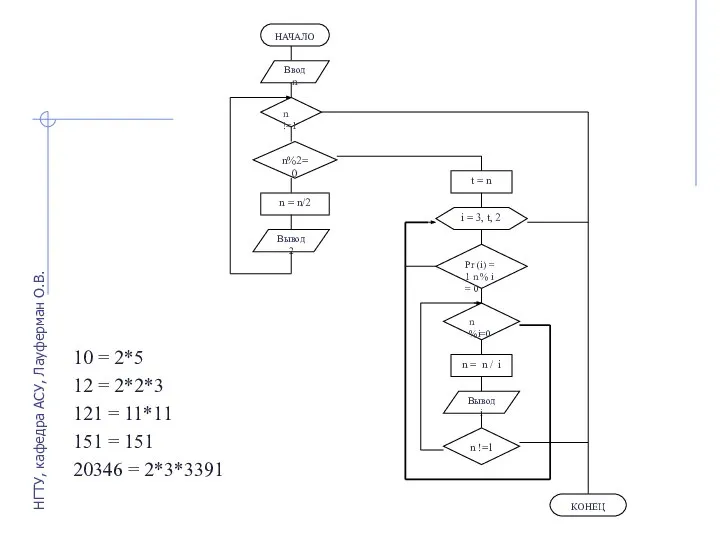
- 7. Известные алгоритмы разложения числа на простые множители являются недетерминированными, так как в них используется метод проб
- 8. 10 = 2*5 12 = 2*2*3 121 = 11*11 151 = 151 20346 = 2*3*3391 НГТУ,
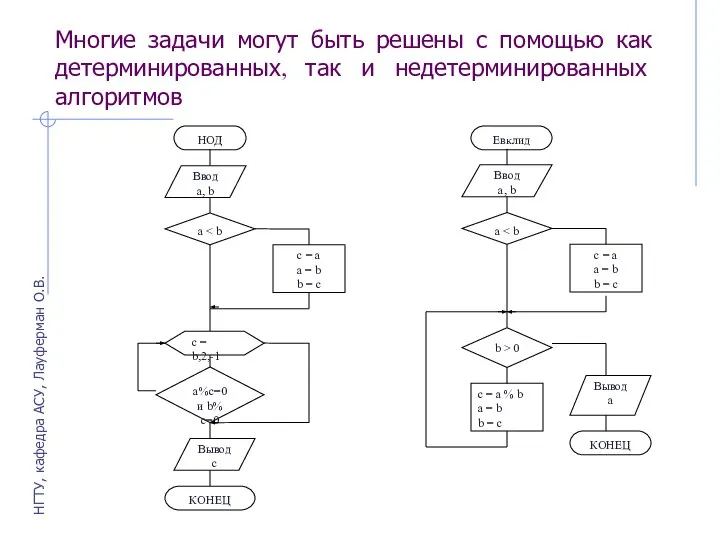
- 9. Многие задачи могут быть решены с помощью как детерминированных, так и недетерминированных алгоритмов НГТУ, кафедра АСУ,
- 10. Методы, используемые для сокращения числа вариантов при переборе или позволяющие выбирать наиболее правдоподобные варианты, называются эвристическими
- 11. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ Все виды обработки могут быть разделены на следующие классы: последовательная обработка, использующая повторения
- 12. Существуют две основные формы повторений: итерация и рекурсия Итерация в основном используется для тех видов обработки,
- 13. Пример 1. Классическим примером рекурсии может служить вычисление факториала в следующем виде: n !=1, для n
- 14. Обе функции имеют линейную сложность. В данном случае итерация предпочтительнее, так как: При каждом рекурсивном вызове
- 15. Пример 2. Две формы реализации алгоритма нахождения наибольшего общего делителя методом Евклида: void Delitel ( int
- 16. Пример 3. Числа Фибоначчи определяются с помощью рекуррентного соотношения: F n + 1 = F n
- 17. В действительности итерация и рекурсия взаимозаменяемы Вывод: следует избегать рекурсии, когда имеется очевидное итерационное решение поставленной
- 18. Свойства рекурсивных алгоритмов Все рекурсивные алгоритмы в целом имеют ряд свойств, которые объединяют их с «рекурсивными
- 19. 1. Рекурсия может быть косвенной программа а ( аргумент х, …) | b ( f (
- 20. 2. Объекты, порожденные рекурсивным определением (информационные структуры или вычисления), должны быть конечными Одна из функций должна
- 21. 3. Должна существовать управляющая величина m, для того чтобы выполнение соответствующей подпрограммы могло быть завершено Это
- 22. Общая методика проведения анализа при решении задачи рекурсивным способом содержит три этапа: параметризация задачи, заключающаяся в
- 23. Пример 1. Вычисление факториала: int fact_rec (int n) // параметризация задачи { if( n == 0)
- 24. Пример 2. Нахождения наибольшего общего делителя методом Евклида: void Delitel ( int a, int b) //
- 25. Пример 3. Формирование чисел Фибоначчи: int Fib_rec ( int n ) // параметризация задачи { if
- 26. Резюме Последовательное прохождение этапов построения рекурсивных алгоритмов: облегчает процесс проектирования и последующего кодирования улучшает читаемость программы
- 27. Параллельная обработка может применяться для: поиска в неупорядоченном массиве с помощью одновременного доступа ко всем элементам
- 28. Структурное распараллеливание с помощью сопрограмм Головная программа передает управление её сопрограмме. После этого управление многократно может
- 29. Сопрограммы, так же как и параллельные процессы, выполняются одновременно Их различие между собой заключается в том,
- 30. МЕТОДЫ ПОСТРОЕНИЯ АЛГОРИТМОВ При разработке алгоритмов следует использовать стандартные подходы. Если метод решения задачи сначала не
- 31. Метод «разделяй и властвуй» Некоторые проблемы по природе своей носят аддитивный характер. Такие проблемы можно разделить
- 32. Метод последовательных приближений (метод подъема) Когда известно приближенное решение и есть способы для его уточнения, можно
- 33. Пример 1. Метод Ньютона-Рафсона для нахождения корней уравнения вида xk – n = 0 Если требуется
- 34. Пример 2. Численное интегрирование Для вычисления интеграла отрезок, на котором он определен, делится на равные части,
- 35. Пример 3. Имеется 25 монет. Все они одного веса, за исключением одной монеты с дефектом, которая
- 36. Метод наискорейшего спуска Метод наискорейшего спуска отличается от метода последовательных приближений тем, что во втором случае
- 37. Метод наискорейшего спуска и метод подъема Использование метода последовательных приближений при создании программ заключается в том,
- 38. Метод обратного прохода (отрабатывания назад) Метод обратного прохода применяется тогда, когда задан порядок (направление) решения некоторой
- 39. Метод поиска с возвратом (программирование с отходом назад) Метод можно описать как организованный исчерпывающий поиск, который
- 40. Метод выделения подцелей (метод частных целей) Метод связан со сведением трудной задачи к последовательности более простых
- 41. Метод выделения подцелей (метод частных целей) Использование подхода «разделяй и властвуй» может служить примером применения метода
- 42. Метод выделения подцелей (метод частных целей) В методе последовательных приближений также используются две подцели. Подцели: найти
- 44. Скачать презентацию







































 Жизненный цикл информационных систем. Основные стадии и этапы разработки ИС и их содержание
Жизненный цикл информационных систем. Основные стадии и этапы разработки ИС и их содержание Instagram для работы
Instagram для работы Внедрение электронного документооборота
Внедрение электронного документооборота Общие сведения о программном обеспечении
Общие сведения о программном обеспечении Изображения в памяти компьютера
Изображения в памяти компьютера Информационные модели систем управления
Информационные модели систем управления  Презентация "Основы логики" - скачать презентации по Информатике
Презентация "Основы логики" - скачать презентации по Информатике Гаджимурадова Жанна Магомедовна учитель информатики МБОУ «СОШ №11» г. Чебоксары Всероссийский сетевой педагогический проект: «А
Гаджимурадова Жанна Магомедовна учитель информатики МБОУ «СОШ №11» г. Чебоксары Всероссийский сетевой педагогический проект: «А Оператор insert
Оператор insert Геоинформационные системы – ГИС. Автор: Дуракова Л.В МБОУ»Ключевская СОШ» Оренбургская область Тюльганский район село Ключи
Геоинформационные системы – ГИС. Автор: Дуракова Л.В МБОУ»Ключевская СОШ» Оренбургская область Тюльганский район село Ключи Понятие алгоритма. Исполнитель алгоритма. Вспомогательные алгоритмы
Понятие алгоритма. Исполнитель алгоритма. Вспомогательные алгоритмы Дети в интернете
Дети в интернете Редактирование, добавление и удаление записей в таблице СУБД MySQL
Редактирование, добавление и удаление записей в таблице СУБД MySQL Работа с таблицами в Microsoft Office Word 2007
Работа с таблицами в Microsoft Office Word 2007 Построение кривой Безье в среде Visual Studio с использованием языка программирования С#
Построение кривой Безье в среде Visual Studio с использованием языка программирования С# Презентация "Компьютерные страдания" - скачать презентации по Информатике
Презентация "Компьютерные страдания" - скачать презентации по Информатике Урок 12. Основи веб-дизайну
Урок 12. Основи веб-дизайну Средства информационных и коммуникационных технологий. Состав персонального компьютера
Средства информационных и коммуникационных технологий. Состав персонального компьютера Основные методы кодирования данных
Основные методы кодирования данных Устройство компьютера
Устройство компьютера Возможность применения ИКТ к основным этапам урока Работу выполнила: Батрак Виктория Викторовна
Возможность применения ИКТ к основным этапам урока Работу выполнила: Батрак Виктория Викторовна Презентация "Информация: виды информации" - скачать презентации по Информатике
Презентация "Информация: виды информации" - скачать презентации по Информатике Система диспетчерского контроля и управления
Система диспетчерского контроля и управления Хранение ИНН и КПП контрагента в документах для обеспечения прозрачности отчетности по НДС
Хранение ИНН и КПП контрагента в документах для обеспечения прозрачности отчетности по НДС Программирование на языке Си. Часть II
Программирование на языке Си. Часть II Искусственный интеллект
Искусственный интеллект СМИ и журналистика
СМИ и журналистика Раздел 2. Общий состав и структура электронно-вычислительных машин и вычислительных систем Тема 2.1 Архитектура ЭВМ и вычислите
Раздел 2. Общий состав и структура электронно-вычислительных машин и вычислительных систем Тема 2.1 Архитектура ЭВМ и вычислите